随着全球范围内的能源紧缺,油价每年不断的大幅上扬[1]。船舶作为交通运输中运量相对较大的运输工具,其能耗问题也越来越突出[2]。其节能的优劣对整个船舶经营收入的整体影响巨大[3]。各个航运巨头为减少能耗,提高营运经济性,对船舶进行改造升级,节能成为当务之急[4]。因此,船舶节能方法现已成为船舶领域研究的重点问题,受到了众多专家学者们的高度关注[5]。
目前,船舶永磁同步电机的主要节能调度方法有:文献[6]提出的利用任务排序的不同计划、不同任务分配的调度算法对船舶电机实现节能调度;文献[7]通过船舶永磁同步电机工况构建电机最小电出力和抽气量之间对应的函数关系,由此建立船舶永磁同步电机节能调度模型;文献[8]提出一种基于遗传算法的多差异嵌入式船舶永磁同步电机的节能调度任务模型,通过功耗最低化理念,利用遗传算法将电机任务以设定的频率分配至不同的嵌入式船舶永磁同步电机中实现处理,实现节能任务调度。上述嵌入式调度方法因船舶永磁同步电机拥有不同的电压可变性,导致调度总能耗较高。
针对上述问题,提出一种基于分阶段的船舶永磁同步电机节点调度方法。实验结果表明,本文算法可最大化限度地减少发电机机组的调控量,从而保障船舶电机机组的稳定运行。
1 最优船舶永磁同步电机机组数目节能调度的要求是既要满足系统负荷需求,又要满足船舶电机机组运行限制,在满足以上方面的基础上,将其一时域的系统负荷适当地分配给指定的船舶电机机组,使船舶电机机组总耗能量最小。具体过程如下:
设定实际运行的船舶电机机组数目为N时船舶永磁电机系统总耗能量
| $ {F_N} = \sum\limits_{i = 1}^N {{F_i}\left( {{P_i}} \right)}\text{,} $ | (1) |
假设共有N + 1台船舶电机机组数时,前N台船舶电机机组的出力将变为:
| $ {P'_i} = {P_i} - \Delta {P_i}\text{,} $ | (2) |
此时域内,船舶电机系统的总能耗表示为:
| $ {F_{N + 1}} = \sum\limits_{i = 1}^N {{F_i}({{P'}_i}) + {F_{N + 1}}({P_{N + 1}})}\text{。} $ | (3) |
最小比耗量可利用以下公式计算求解。根据消耗量特殊属性曲线视为切线,切线交于点B(P0,F0),B(P0,F0)的比耗量就是最小比耗量,且与此点的耗量微增率相等。设定直线OB的方程是F=kP,那么对于耗量特殊属性曲线
| $ {\mu _{\min }} = 2a{P_O} + b\text{,} $ | (4) |
求解方程组:
| $ \begin{array}{l} {F_0} = aP_0^2 + b{P_0} + c\text{,} \\ {F_o} = k{P_0}\text{,} \\ k = 2a{P_0} + b\text{,} \end{array} $ | (5) |
通过式(5)求解可得到
| $ {\mu _{\min }} = 2\sqrt {ac} + b\text{。} $ | (6) |
依据上述船舶电机机组融入准则,即可确定船舶永磁同步电机系统负荷变化时融入计算的最优船舶永磁同步电机机组数目。
2 船舶永磁同步电机节能调度方法的设计在最优船舶永磁同步电机机组数量确定的前提下,对嵌入式船舶永磁同步电机的耗量特征进行排序并构建等微增率基准,将微增率基准与最优潮流相结合,有效处理限制条件并降低系统电机能耗,在满足限制基准的基础上,进行船舶永磁同步电机的嵌入式节能调度的全局最优解。
2.1 船舶永磁同步电机各机组的经济运行点的计算将等微增率原理应用于船舶永磁同步电机节能调度的第1阶段:将NG个发电模块的输入/输出特征分别表示为
| $ \min F = \sum\limits_{i = 1}^{NG} {{F_i}\left( {{P_{Gi}}} \right)} \text{,} $ | (7) |
| $ \sum\limits_{i = 1}^N {{P_{Gi}} = {P_D}} \text{。} $ | (8) |
利用拉格朗日乘数法计算获取式(7)及限制条件的最优问题式(8),可得拥有最小微增率的拥有多层发电模块的经济运行点如下式:
| $ \frac{{{\rm d}{F_i}}}{{{\rm d}{P_{Gi}}}} = \lambda i = 1, 2, \cdots, N\text{,} $ | (9) |
| $ \frac{{{\rm d}{F_1}}}{{{\rm d}{P_{G1}}}} = \frac{{{\rm d}{F_2}}}{{{\rm d}{P_{G2}}}} = \cdots \frac{{{\rm d}{F_N}}}{{{\rm d}{P_{GN}}}} = \lambda\text{。} $ | (10) |
通过式(9)和式(10)进行求解即可得到第一阶段船舶永磁同步电机各机组的经济运行点PGi0。
2.2 嵌入式节能调度的全局最优解的实现第2阶段实质是将微增率基准与最优潮流相结合,有效处理限制条件并降低系统电机能耗,在满足限制基准的基础上,进行船舶永磁同步电机的嵌入式节能调度的全局最优解。
基于船舶永磁同步机组综合能耗微增率的单个时域内ESGD目标函数为此时域内系统机组发电能耗最低。具体过程如下:
通过式(11)分析网络损失因素,
| $ \sum\limits_{i = 1}^G {{P_{Gi}} - } \sum\limits_{i = 1}^N {{P_{Li}} = L}\text{,} $ | (11) |
式中:G为船舶永磁同步电机机组数目;N为节点数目;L为船舶永磁同步电机系统网损。将构建此优化问题的拉格朗日函数表示为:
| $ F = \frac{G}{{i = 1}}{f_i}\left( {{P_{Gi}}} \right) - \beta \left[{\sum\limits_{i = 1}^G {{P_{Gi}}-} \sum\limits_{i = 1}^G {{P_{Li}}-L} } \right]\text{,} $ | (12) |
通过式(12)可获得最小值的条件,将两类条件分别通过式(13)和式(14)所示:
| $ \frac{{\partial F}}{{\partial {P_{Gi}}}} = 0, i = 1, 2, \cdots, G\text{,} $ | (13) |
| $ \frac{{\partial F}}{{\partial \beta }} = 0\text{。} $ | (14) |
等式的限制条件如式(13)所示,式(13)可表示为式(15):
| $ \frac{{\Delta {f_i}\left( {{P_{Gi}}} \right)}}{{\Delta {P_{Gi}}}} - \beta + \beta \frac{{\Delta L}}{{\Delta {P_{Gi}}}} = 0\text{,} $ | (15) |
| $ \beta = \frac{{\Delta {f_i}\left( {{P_{Gi}}} \right)}}{{\Delta {P_{Gi}} - \Delta L}} = \frac{{\Delta {f_i}\left( {{P_{Gi}}} \right)}}{{\sum {\Delta {P_{Li}}} }}\text{。} $ | (16) |
通过式(16)可知目标函数取最小值时,
设定船舶电机机组集合不改变且无需分析网络限制的前提下,第1时段出力分配的ESGD最优条件如下:
充分不必要基准:船舶电机机组拥有一致地综合能耗微增率;
必要不充分基准:没有出力约束船舶电机机组拥有一致的综合能耗微增率;
充分必要基准:
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda _i} = \lambda ,i = 1 \sim M,}\\ {{\lambda _u} < \lambda ,u = M + 1 \sim S,}\\ {{\lambda _d} > \lambda ,d = S + 1 \sim K.} \end{array}} \right. $ | (17) |
式中:M为将出力的且没有受到上下限限制的船舶电机机组数目;i为船舶电机机组序位,
式(17)表示在船舶永磁同步电机系统设定负荷情况下,船舶电机各机组出力分配需要遵从综合能耗微增率的基本准则。依据此准则实现分配船舶电机机组出力时,将综合能耗微增率小的船舶电机机组增加出力,使得系统能耗上升空间很小,因此应该增大出力,直至可满足船舶电机下限;没有受船舶电机机组出力上下限限制的机组应该拥有一致的综合能耗微增率。
在实际对发电机组进行边策发电计划时,为实现多个时段优化问题,对目标函数实质为船舶永磁同步电机运行时域内综合能耗率最低,此时域的限制条件需融入船舶电机机组爬(下)坡限制。设定船舶电机系统出力分配策略为
充分不必要基准:
基准1:
基准2:独立时域t内出力分配解如果没有满足ESGD最优性基准时(Xt-1同Xt + 1都满足单一时域ESGD最优性基准),对船舶电机机组爬坡限制的前提条件不做考虑的情况下,对时域t实现出力分配,获得
基准3:独立时域t处理分配解Xt不能够满足单一时段ESGD最优性基准,如果Xt(1)同Xt–1之间有一个船舶机组不满足爬坡限制,则将此类船舶机组序位放置于集合内。
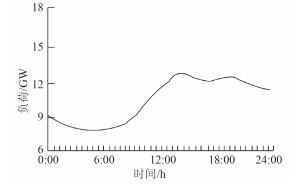
3 实验结果与分析利用IEEE118节点系统表述利用本文算法调整船舶永磁同步机组的合理性。该系统中船舶电机机电组50台,设定装机容量为1 800 MW,占全部装机总量的80%。单个船舶电机供电标准能耗在[300~450]g/(kw·h)范围内。将本文提出的节能算法与节能排序方法进行负荷分配,如图 1所示为50点日负荷趋势图, 部分船舶电机机组的运行参数通过表 1所示。
|
图 1 系统日负荷曲线 Fig. 1 Daily load curve of electric power system |
|
|
表 1 火电机组运行参数 Tab.1 Thermal power unit operation parameters |
因节能排序法利用基础必备的船舶电机机组台数确定机组集合,依据机组各个时段的最大爬、降坡能力分配负荷。如图 1所示IEEE118节点系统负荷在时段内时一个持续降坡阶段,因序位靠后的部分船舶电机机组已经在出力下限实行,此时系统负荷的降幅通过序位靠前的电机机组来平衡。
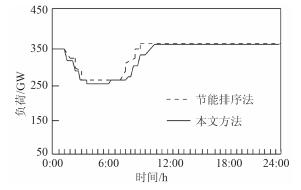
依据先验知识,设置机组持续时段数目为5,如图 2~图 4所示为利用2种节能算法分配的结果对比。
|
图 2 机电组A(发电序号1) Fig. 2 Mechanical and electrical group A (generating sequence number 1) |
|
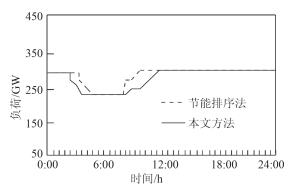
图 3 机电组B(发电序号12) Fig. 3 Mechanical and electrical group B (power generation number 12) |
|
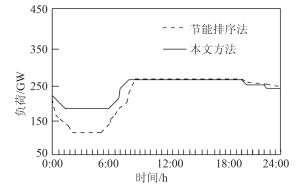
图 4 机电组C(发电序号28) Fig. 4 Mechanical and electrical group C (power generation number 28) |
通过图 2~图 4可看出,节能排序法使序位靠前的船舶电机机组快速降至最低,因夜间的低谷要维持一段时间,因此降低了高序位的发电负荷率;同时在5:00-11:00时域内系统负荷迅速增加,综合爬坡可达5 236 MW,致使高序位的电机机组运用最大的爬坡能力调整峰值后,相应的负荷仍然降不下来,增加了低序位机组的发电负荷率。而本文方法通过对嵌入式船舶永磁同步电机的耗量特征进行排序并构建等微增率准则,将微增率原则与最优潮流结合,由此增加了低序位机组的发电负荷率。
将本文方法与节能排序法计算的对比结果通过表 2所示,与节能排序法相比可知,本文方法总能耗量由43 033降至42 025,节约标准煤1 008 t,具有相当不错的节能效果。
|
|
表 2 两种节能方法计算结果对比表 Tab.2 Two methods of energy saving calculation results contrast table |
本文通过分析嵌入式调度方法应用于船舶永磁同步电机形成的缺陷,提出一种基于两阶段的船舶永磁同步电机节点调度方法。该方法先对嵌入式船舶永磁同步电机的耗量特征进行排序并构建等微增率准则,将微增率原则与最优潮流结合,实验结果表明,该算法最大限度地减少发电机组的调节量,有助于维持机组稳定运行。
| [1] |
周京阳, 王斌, 周劼英, 等. 市场机制下智能电网调度控制系统调度计划应用模型及分析[J]. 电力系统自动化 , 2015, 39 (1) :124–130.
ZHOU Jing-yang, WANG Bin, ZHOU Jie-ying, et al. Applied model and analysis of dispatching plan in smart grid dispatching and control systems under market mechanism[J]. Automation of Electric Power Systems , 2015, 39 (1) :124–130. |
| [2] |
陈聪, 陈堃, 葛志超, 等. 云南电网考虑负荷近区平衡的节能优化调度动态稳定性分析[J]. 陕西电力 , 2014, 42 (6) :55–59.
CHEN Cong, CHEN Kun, GE Zhi-chao, et al. Energy-saving optimized dispatching dynamic stability analysis considering load balanced nearby in Yunnan power grid[J]. Shaanxi Electric Power , 2014, 42 (6) :55–59. |
| [3] |
彭祖辉, 孙栓柱, 代家元. 火电机组节能发电调度决策支持系统研究与开发[J]. 中国电力 , 2014, 47 (5) :107–112.
PENG Zu-hui, SUN Shuan-zhu, DAI Jia-yuan. R & D of decision-making supporting system for energy-saving thermal power generation dispatching[J]. Electric Power , 2014, 47 (5) :107–112. |
| [4] |
蒋寻寒, 张辉, 田万军, 等. 火电机组节能调度的技术框架研究[J]. 中国电力 , 2014, 47 (6) :140–144.
JIANG Xun-han, ZHANG Hui, TIAN Wan-jun, et al. Study on technical framework of thermal power unit energy-saving dispatch[J]. Electric Power , 2014, 47 (6) :140–144. |
| [5] |
黄日胜. 异构并行系统中高时效性任务的节能调度方法[J]. 计算机应用与软件 , 2015, 32 (11) :329–333.
HUANG Ri-sheng. Energy-saving scheduling method for tasks with high time effectiveness on heterogeneous parallel system[J]. Computer Applications and Software , 2015, 32 (11) :329–333. |
| [6] |
高赐威, 梁甜甜, 李扬. 节能发电调度下基于虚拟机组的日前负荷调度模型[J]. 中国电机工程学报 , 2014, 34 (22) :3691–3699.
GAO Ci-wei, LIANG Tian-tian, LI Yang. Model of day-ahead load scheduling based on virtual generator unit in energy-saving power generation dispatching[J]. Proceedings of the CSEE , 2014, 34 (22) :3691–3699. |
| [7] |
许政强, 胡林献. 热电机组最小电出力计算方法及在节能调度中的应用[J]. 节能技术 , 2014, 32 (6) :500–505.
XU Zheng-qiang, HU Lin-xian. Study on the least electrical output of thermoelectric unit and application on grid energy-efficient scheduling[J]. Energy Conservation Technology , 2014, 32 (6) :500–505. |
| [8] |
郑巧彦. 多差异嵌入式设备的节能任务调度模型仿真[J]. 计算机仿真 , 2015, 32 (3) :426–429.
ZHENG Qiao-yan. Simulation of energy-saving task scheduling model for multi-difference embedded device[J]. Computer Simulation , 2015, 32 (3) :426–429. |
| [9] |
聂亚飞, 姚锡凡, 周际锋. 基于BPEL和Drools的车间调度研究[J]. 电子设计工程 , 2014, 22 (9) :51–53.
NIE Ya-fei, YAO Xi-fan, ZHOU Ji-feng. Research on job-shop scheduling based on BEPL and Drools[J]. Electronic Design Engineering , 2014, 22 (9) :51–53. |
 2016, Vol. 38
2016, Vol. 38
