截止阀具有制造简单、价格便宜、调节性能好等特点,被广泛应用于船舶的海水、液压、滑油、空气等管路系统,起到改变管路断面和介质流动方向,控制输送介质流量与压力等作用[1-3]。截止阀可分为直通式、直角式和直流式[4]。而直通截止阀主要用于直线管路,特点是便于施工操作,但由于直通截止阀的内部结构相对于管路系统的其它结构远为复杂,因此对管路系统的内部流场有较大影响,它不仅可以降低流体的流速和流量,还会由于漩涡不稳定分离、湍流脉动等非定常因素导致流场压力发生脉动,进而导致管路系统的振动噪声[5-7]。
因此,本文选取实际装有CB855A-DN80直通截止阀的管路系统为研究对象,应用计算流体力学通用软件Fluent,采用大涡模拟算法进行流场与水动力噪声分析,预报直通截止阀的流阻系数、管路系统的流场压力、流场流速和水动力噪声情况,旨在为保证CB855A-DN80直通截止阀在舰船管路系统的顺利应用奠定技术基础。
1 有限元模型的建立本文应用Fluent有限元软件,建立的管路系统仿真计算模型如图 1所示。该管路系统包括管路与阀门2部分,其中直通截止阀的型号为CB855A-DN80,管路直径80 mm,阀道入口前的管路长度取阀道入口直径的5倍,阀道出口后的管路长度取阀道出口直径的10倍。采用四面体与六面体混合网格结构类型进行网格化分。在边界条件设置时,入口采用速度入口边条,给定所要求的入口处速度值,出口采用OUTFLOW边条;阀体与阀芯的壁面采用固壁边界条件,同时在数值计算中采用壁面函数的近壁处理方法。流道内流体温度设定为15 ℃,密度为1 025.9 kg/m3,物理粘度为1.188 3 × 10-6m2/s,流速分别设定为0.97 m/s,1.93 m/s,3.09 m/s。

|
图 1 计算模型 Fig. 1 Calculation model |
2流场分析
结合流场数值仿真计算,根据国家行业标准《通用阀门流量系数和流阻系数的试验方法》(JB/T 5296-91)对各型阀门流阻系数计算公式(1)的规定,算出该管路系统的流阻系数:
| $ {{K}} = \frac{{2 \Delta {{P}}}}{{{\rm{\rho }}{{{v}}^2}}}\text{。} $ | (1) |
式中:ΔP为水流经阀门时的压力降;ρ为流体密度;v为流体速度。
为更好地描述该管路系统的流场压力和流速分布情况,从阀道出口位置开始,每隔1倍管径距离,将右侧管道内流体依次划分为11个剖面,具体如图 2所示。

|
图 2 剖面位置 Fig. 2 Section place |
为更好地描述流场压力情况,引入压力平均值、压力均方根和无量纲压力均方根的公式如下:
| $ {p_{mean}} = \frac{1}{A}\int_A {p{\rm d}a} \text{,} $ | (2) |
| $ {p_{rmse}} = \sqrt {\frac{1}{A}\int_A {{{\left( {p - {p_{mean}}} \right)}^2}{\rm d}a} } \text{,} $ | (3) |
| $ C{p_{rmse}} = \frac{{{p_{rmse}}}}{{0.5\rho {v^2}}}\text{。} $ | (4) |
式中:ρ为流体密度,v为入口速度。
2.1 流阻系数分析流阻系数是反映阀门对流场影响的重要指标,体现了阀门对管路系统造成的压头损失。直通式截止阀(CB855A-DN80)流阻系数计算结果见表 1。
|
|
表 1 流阻系数 Tab.1 Flow resistance coefficient |
由表 1可知,直通式截止阀(CB855A-DN80)的流阻系数随流体流速的增大呈逐渐减小的趋势,但数值变化不大。当流速为0.97 m/s时,阀门的流阻系数为最大值5.2。
2.2 流场压力分析当流场流速分别为0.97 m/s,1.93 m/s,3.09 m/s时,整个管路系统的流场压力分布情况如图 3所示。由图 3可知,在这3种流速下,流体压力的分布趋势相同。对于流向阀门的流体压力来说,由于流体流速恒定,因此远离阀道入口处的流场压力比较稳定。阀道入口弯管段的流场压力梯度较大,其中弯管上部的流体压力较小,而弯管下部的流体压力较大,这是由于阀门入口段的弯管结构阻碍了流体的流动方向,使得流体在流道内产生紊流引起的。阀芯四周的流场压力较小,而阀道出口段的流场压力最小。这是由于阀芯阻碍了流体的流动,使得流体在负压的作用下流体压力变小。
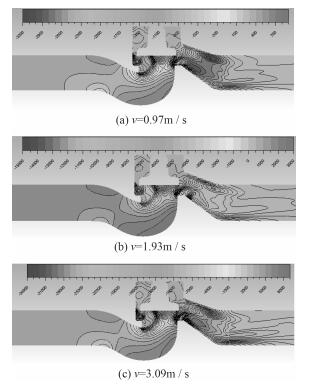
|
图 3 不同流速下流场压力分布云图 Fig. 3 Flow field pressure distribution in different velocity |
为进一步掌握阀道出口右侧的管内流场压力分布情况,图 4显示了各剖面位置的流场压力分布情况。从图 4可以看出,阀道出口附近的流场压力波动较大,随着距阀道出口距离的增大,同一剖面的流场压力逐渐趋于平稳。

|
图 4 不同剖面的压力分布云图 Fig. 4 Pressure distribution in different sections |
通过提取各剖面的流场压力数据,并绘制压力均方根、无量纲压力均方根与流场剖面位置(0 -10D)的关系曲线如图 5和图 6所示。
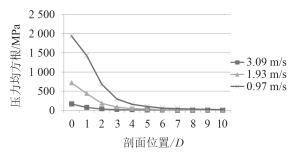
|
图 5 压力均方根的变化趋势 Fig. 5 The changing current of pressure RMS |
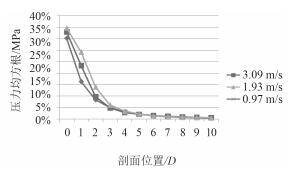
|
图 6 无量纲压力均方根变化趋势 Fig. 6 The changing current of dimensionless pressure RMS |
由图 5可知,从整体上来说,当流速分别为v=0.97 m/s,v=1.93 m/s,v=3.09 m/s时,3条压力均方根曲线的变化,均呈现逐渐下降的趋势。在管路出口段0~5D区间范围内,流场压力均方根变化梯度较大,尤其是流速V=0.97 m/s时的流场压力均方根变化梯度最大。在管路出口段7~10D区间范围内,流场压力均方根变化趋于平稳,且3条压力均方根曲线几乎重合在一起。
由图 6可知,从整体上来说,当流速分别为v=0.97 m/s,v=1.93 m/s,v=3.09 m/s时,3条无量纲压力均方根曲线的变化趋势相同,均呈现逐渐下降的趋势。在管路出口段4~10D区间范围内,流体的无量纲压力均方根数值相接近,3条曲线几乎重合在一起。
2.3 流速分析整个管路系统的流体流速分布如图 7所示。由图 7可知,靠近阀芯左下角有一个明显的小漩涡,而在阀芯四周(图 7中阀芯左侧位置)有一个大漩涡。阀门进口段的流体流速方向一致,而靠近圆弧上壁的流速略为偏大。在阀芯右下角出口附近,由于流道截面积突然变小,使得流体的流速迅速变大。阀门出口段的流体由两部分构成,一部分来源于阀门入口段的流体,另一部分来源于阀芯四周的流体,两者的流向均是从两侧逐渐向中心合龙。

|
图 7 流速分布云图 Fig. 7 Flow velocity distribution |
当流速分别为v=0.97 m/s,v=1.93 m/s,v=3.09 m/s时,整个管路系统的水动力噪声声压级如表 2所示。由表 2可知,随着流体流速的增大,整个管路系统的水动力噪声声压级逐渐增大。
|
|
表 2 不同流速的水动力噪声声压级数据 Tab.2 The hydrodynamic noise sound pressure level in different flow velocity |
图 8显示了整个管路系统的水动力噪声声压级分布情况。由图 8可知,当流速分别为v=0.97 m/s,v=1.93 m/s,v=3.09 m/s时,整个管路系统的水动力噪声声压级分布趋势相同,即阀门内的水动力噪声声压级分布情况复杂,且水动力噪声声压级数值较大,这是由于阀门内流体压力和速度变化较大,且阀芯四周存在涡流现象造成的。可见直通截止阀引起的流体噪声是整个管路系统的主要噪声,因此,消除直通截止阀引起的流体噪声是管路系统降噪的重点。
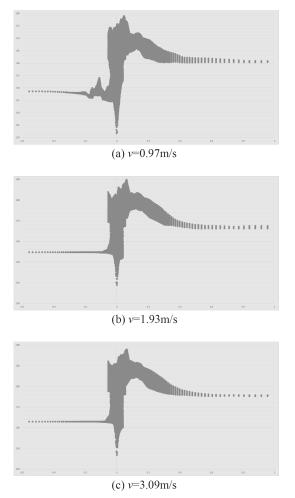
|
图 8 水动力噪声声压级分布图 Fig. 8 The hydrodynamic noise sound pressure level distribution |
1)直通式截止阀的流阻系数随流体流速的增大呈逐渐减小的趋势,但数值变化不大。
2)在阀芯右下角出口附近,由于流道截面积突然变小,使得流体的流速迅速变大。
3)随着流体流速的增大,水动力噪声声压级逐渐增大。
| [1] |
袁新明, 贺治国, 毛根海. 用RNG k-ε紊流模型对截止阀三维紊流流动的数值模拟[J]. 流体机械 , 2006, 34 (2) :34–38.
YUAN Xin-ming, HE Zhi-guo, MAO Gen-hai. Numerical simulation of a turbulence flow in the cut-off valve by RNG k-ε turbulence model[J]. Fluid Machinery , 2006, 34 (2) :34–38. |
| [2] |
张玉祥, 杨柳. 截止阀的建模与仿真实现[J]. 流体机械 , 2007, 35 (12) :29–31.
ZHANG Yu-xiang, YANG Liu. Modeling and simulation implementation of stop valve[J]. Fluid Machinery , 2007, 35 (12) :29–31. |
| [3] | 杨源泉. 阀门设计手册[M]. 北京: 机械工业出版社, 2000 . |
| [4] | 陆培文. 实用阀门设计手册[M]. 北京: 机械工业出版社, 2007 . |
| [5] | 袁新明, 毛根海, 张土乔. 阀门流道流场的数值模拟及阻力特性研究[J]. 水力发电学报 , 1999 (4) :60–66. |
| [6] | 张少凯, 蔡敬标, 方志刚. 舰船通用阀门"三漏"防治之我见[J]. 舰船科学技术 , 2001, 23 (5) :57–61. |
| [7] |
崔铭超, 唐科范, 刘桦. 基于CFD技术的阀门内流道优化[J]. 水动力学研究与进展 , 2010, 25 (4) :438–445.
CUI Ming-chao, TANG Ke-fan, LIU-Hua. Optimization of the valve internal flow channel based on CFD approach[J]. Chinese Journal of Hydrodynamics , 2010, 25 (4) :438–445. |
 2016, Vol. 38
2016, Vol. 38
