2. 上海交通大学 海洋工程国家重点实验室, 上海 200240
2. State Key Lab of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China
随着海洋油气的开采逐渐向深海推进,顺式系统(由大量通过系泊缆线与海床连接的浮式系统组成)正在逐渐取代常规的重力系统。这些顺式系统的应用,发展出了大量的新型立管,钢悬链线立管是其中最常用的一种。
与其他立管相比,钢悬链线立管有如下优点:1)与平台的连接更为灵活,无需额外的附加装置,只需通过柔性接头,即可自由悬挂在平台外,可充分利用平台空间;2)成本更为低廉,与传统的TTR(顶张紧立管)相比,采用钢悬链线立管的深海钻油平台可降低成本10万英镑以上[1]。上述优点,使得钢悬链线立管的应用越来越普遍。
国内针对钢悬链线立管整体疲劳损伤分析还处于起步阶段。杜金新[5]和杨和振[6]采用弹性力学理论,将钢悬链线立管触地段和触地段土体简化成管-线性弹簧作用模型,分析钢悬链线立管触地段的静力特性及静态疲劳损伤,但并没有考虑管土作用复杂的非线性因素。傅俊杰[7]将触地段土体用非线性弹簧模拟,较好地反映了管土作用的非线性现象,但没有涉及到土体对管的土体吸力作用,且只对触地点的动力响应进行分析,对管上其他重要位置并没有予以考虑,钢悬链线立管的整体疲劳分析并没有得到很好的体现。本文根据Ansys有限元分析软件的特点,利用其中的combin 39和pipe 59单元来分别模拟触底段土体和立管模型,采用Bridge[8]文中的土体吸力理论和Aubeny[9]的管土作用P-y模型,对钢悬链线立管的实际运动载况进行有限元模拟,分析立管上若干重要节点在钢悬链线立管承受剪切流和顶部简谐运动下的动态响应及疲劳损伤。具体分析步骤如下:1)根据解算出的立管系统模态频率,求解立管系统的阻尼系数;2)模拟实际载况,对立管有限元模型施加动力载荷,分析不同载况下立管上重要节点处的动态响应;3)采用疲劳理论,解算出立管在海洋环境载荷下的疲劳损伤寿命。
1 基本理论在钢悬链线立管的设计过程中,钢悬链线立管的疲劳分析应被重点考虑[2]。在使用时,钢悬链线立管的疲劳损伤主要是由浮体运动及海洋环境载荷造成的。研究表明,钢悬链线立管上最易遭受疲劳破坏的部位分别为钢悬链线立管顶端与平台相连的部分以及底端与海床接触的区域[3]。
由于海床土体的可压缩性以及钢悬链线立管的自重,在钢悬链线立管下端与海床土体相接触的部位,该部位的海床由于承受立管下端的自重而产生一段向下凸的沟渠。初始沟渠的大小和形状与立管自重以及土体特性密切相关[4]。
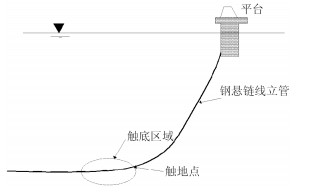
沟渠的存在,使得钢悬链线立管与海床土体相接触的部位,而触地段(见图 1)承受复杂的受力变化,对钢悬链线立管的疲劳损伤有着重要的影响。国内外已有不少专家对此进行专门研究。
|
图 1 钢悬链线立管管土作用示意图 Fig. 1 SCR pipe-soil interaction sketch |
实际工况下,钢悬链线立管的动力响应方程如下:
| $ {\boldsymbol{M}} \mathop U\limits^{..} \ + {\boldsymbol{C}} \mathop U\limits^. \ + {\boldsymbol{K}} U\ = \ F(t)\text{,} $ | (1) |
式中:M为质量矩阵;
本文根据实际情况,采用工程上常用的瑞利阻尼[10]:
| $ {\boldsymbol{C}} = \alpha {\boldsymbol{M}} + \beta {\boldsymbol{K}}\text{,} $ | (2) |
式中:α与β为阻尼系数,由振型阻尼比和系统固有角频率决定:
| $ \xi = \frac{\alpha }{{2{\omega _i}}} + \frac{{\beta {\omega _i}}}{2}\text{,} $ | (3) |
式中:
C. Sparks[11]分析认为,在实际海洋载荷环境下,立管所承受载荷可用等效应力表达如式(4):
| $ {\sigma _{vm}}^2 = {({\sigma _{le}} + {\sigma _{ab}})^2} + 3{\tau ^2}\text{,} $ | (4) |
式中:
钢悬链线立管触地段的管土作用涉及到十分复杂的非线性原理。Aubeny等[8]通过实验观察,发现管土作用模型可用下式来描述:
| $ EI\frac{{d{}^4y}}{{d{x^4}}} = W-P\text{,} $ | (5) |
式中:E,I和W分别为单位长度立管的弹性模量、惯性矩和重量;P为单位长度土体反力,可由下式得到:
| $ P = Da{(y/D)^b}({c_0} + \rho y)\text{。} $ | (6) |
式中:D为立管管径;y为立管在外载作用下的垂向位移;ρ为土体刚度梯度系数;c0为海床土体的未排水剪切刚度系数;a和b之值与立管管壁粗糙度及y/D之值密切相关。
根据式(5),可以得到管土作用的位移—反力曲线,即P-y曲线,Dunlap[12]通过实验观察验证了该曲线。在实际分析计算中,一般用式(5)来描述立管触地段的土体反力—位移变化历程。
立管触地段不仅受到土体反力的作用,当触地段脱离土体向上运动的时候,还会受到海床土体对其作用的向下的土体吸力[9]。土体吸力的存在,对立管的疲劳损伤也有相应影响。
立管的疲劳损伤在很大程度上也受与其接触的海床土体特性影响,Bridge[13]指出,立管的疲劳损伤随土体刚度的增大而增大。土体刚度主要由土体特性参数c0和ρ决定,与这两者呈正相关。
由式(1)及式(5),求出立管在海洋环境载荷下的动力响应后,可采用S-N曲线及Palmgren Miner疲劳损伤理论求解立管的疲劳寿命,常用的S-N曲线见式(7):
| $ \log (N) = \log ({a_1})-m\log (S)\text{,} $ | (7) |
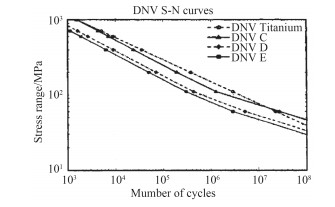
式中:N为在疲劳应力作用下的疲劳寿命;S为疲劳应力;a与m为材料常数,可根据实验得到。根据DNV规范[14],本文选取图 2中的C曲线。
|
图 2 DNV规范中的S-N曲线 Fig. 2 S-N curves by DNV |
Palmgren Miner疲劳损伤理论为:
| $ D = \sum {\frac{{n({S_i})}}{{N({S_i})}}}\text{,} \;\;\;(i = 1, 2, ...k)\text{。} $ | (8) |
式中:D为立管在整个工作期间所承受的总疲劳损伤;N(Si)为在Si作用下的疲劳寿命,由选定的S-N曲线确定;n(Si)为应力幅值Si作用下的循环次数,由立管实际承受的载荷谱给出。
当D=1时,立管将疲劳失效。因此立管的疲劳寿命可用下式描述:
| $ \lambda = 1/(\sum {n({S_i}} )/N({S_i}))\text{。} $ | (9) |
本文算例中的立管具体参数见表 1。
|
|
表 1 立管参数 Tab.1 Parameters of SCR |
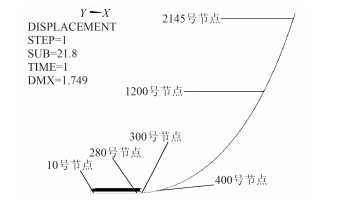
图 3为钢悬链线立管在自重及外载作用下的有限元模型,在该模型中,根据立管的实际受载及运动情况,约束立管顶端的Y向位移,约束触地段井口处的X及Y向位移。海床土体采用最常见的墨西哥湾中等强度土:c0=3.0 kPa,ρ=1.3 kPa/m。考虑到极端情况造成的破坏性影响,立管系统承受的洋流载荷选为墨西哥湾百年一遇季风条件下的剪切流[15],流速为1.55 m/s。除洋流外,与立管顶端连接的海洋平台在风浪及洋流的作用下,会产生复杂的升沉运动,可由浮体运动的线性理论将上述升沉运动简化为一系列简谐运动的叠加[16]。在规则波浪作用下,与该立管连接的海洋平台的运动可视为竖向的简谐运动[17]:z=4.55 sin(0.365 t)。本文算例中立管的实际受载情况可看成上述洋流载荷及简谐运动载荷的叠加。
|
图 3 钢悬链线立管有限元模型 Fig. 3 FEM model of SCR |
对该钢悬链线立管的有限元模型进行解算,求出立管系统的第一阶和第二阶模态频率,代入式(3),联立求解方程组,可求出阻尼系数α和β分别为0.002 9和0.277 9。
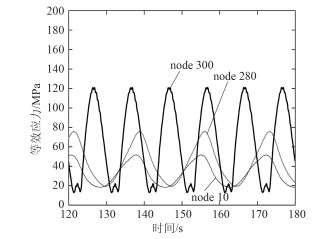
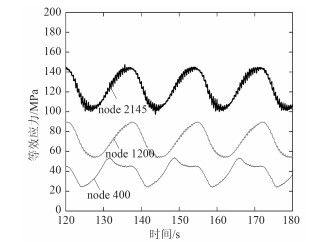
2.2 管上关键节点的应力时程曲线图 4和图 5给出了管上关键节点的应力时程曲线:触地点处的300号节点、距触地点左端20m处的280号节点、触地段距左边井口10m处的10号节点、悬垂段下端距触地点100m处的400号节点、悬垂段中段的1 200号节点、距悬挂点5m处的2 145号节点。分析上述曲线可以看出:触地点和悬挂点是立管上的敏感点,该两处部位承受更大的应力幅值,相比较立管上的其他点而言,承受的疲劳载荷也更为强烈,为钢悬链线立管的疲劳热点部位,在立管系统的设计过程中应给予重点考虑。距悬挂点和触地点越近的部位,所承受的疲劳载荷也越大。在外载的反复作用下,立管触地段与海床不断循环接触,触地点的位置也不断发生变动,故悬垂段下端的400号节点的应力变化也较大。从上述曲线中还可以看到,触地点及400号节点处的等效应力沿峰值处产生轻微的波动,该波动主要由土体吸力引起。立管触地段完全脱离土体后,此时土吸力不再起作用,所承受的应力幅值也会减小。洋流冲击引起的应力激荡使得立管悬垂段中段的1 200号节点及悬挂点附近的2 145节点处的应力时程曲线呈现明显的锯齿状,越靠近海面处,洋流速度越大,应力激荡越厉害;海底的洋流流速很小,触地段上各点的应力时程曲线上的锯齿状并不明显。
|
图 4 考虑土体吸力的触地段上各点应力时程曲线 Fig. 4 Stress-time curve of nodes in TDZ considering soil suction |
|
图 5 考虑土体吸力的悬垂段上各点应力时程曲线 Fig. 5 Stress-time curve of nodes in hanging part considering soil suction |
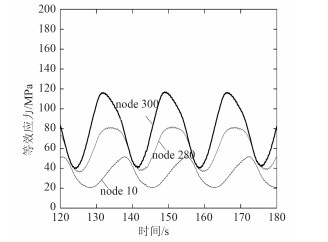
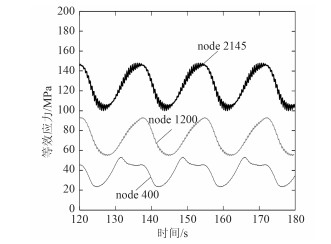
分析土体吸力对立管疲劳损伤的影响时,仍选取上述节点进行分析。图 6~图 7描述了不计及土体吸力时立管上各点处的应力时程曲线。从图中可看到,此时立管触地段上各点的应力幅值和应力变化明显小于考虑土体吸力时的应力幅值和应力变化。因土体吸力只在触地段与海床土体接触部位存在,故只有触地点及附近区域的疲劳损伤受土体吸力的影响较为明显,立管上其他部位受其影响并不显著;此时,不考虑土体吸力作用的触地点处的等效应力时程曲线没有出现没有出现图 4中峰值处的应力波动,这是因为没有土体吸力的作用。
|
图 6 无土体吸力的触地段上各点应力时程曲线 Fig. 6 Stress-time curve of nodes in TDZ without soil suction |
|
图 7 无土体吸力的悬垂段上各点应力时程曲线 Fig. 7 Stress-time curve of nodes in hanging part without soil suction |
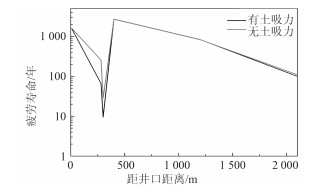
土体吸力对立管疲劳寿命的影响如图 8所示,图中反映土体吸力的存在会减小立管触地段尤其是触地点的疲劳寿命;对触地段以外的其他部位而言,土体吸力对疲劳寿命的影响并不显著;触地点及其附近区域的疲劳寿命在整个立管范围内最小;此外,风浪及洋流载荷对海平面附近区域即悬垂段上端的作用最强,使得立管悬挂段上段的疲劳寿命也相对较小。这也表明在立管设计过程中对悬挂段上段以及触地点附近区域应重点考虑。
|
图 8 土体吸力对立管疲劳寿命的影响 Fig. 8 The effect of soil suction on fatigue life of SCR |
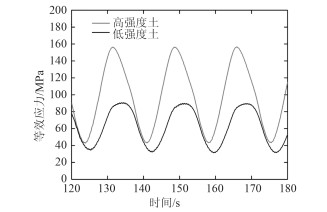
前文已经提及,钢悬链线立管的疲劳损伤寿命在很大程度上由与触地段接触的土体刚度决定。截至目前,钢悬链线立管已在全球范围内广泛应用,不同海洋环境下的土体特征差异较大。下面以墨西哥湾中常见的2种土体为例:低强度土,c0=1.2 kPa,ρ=0.8 kPa/m;高强度土,c0=3.8 kPa,ρ=2.0 kPa/m,分析立管触地点及悬挂点附近区域在不同土体特性下的应力变化。不同土体特性下对应的触地点和悬挂点的应力时程响应曲线见图 9和图 10。从图中可得到以下重要结论:钢悬链线立管触地点的应力变化幅值受土体特性较为显著的影响,触地点在高强度土体下的应力变化和应力幅值几乎是在低强度土体下的2倍;对应的高强度土体下触地点的疲劳寿命为7.9年,低强度土下触地点的疲劳寿命为61.4年,高强度土体下触地点的疲劳寿命约为低强度土的13%,表明高强度土下立管触地段疲劳损伤更为明显。此外,从图中还可以发现,悬挂点处的应力时程在不同土体下几乎没有变化。这也进一步验证了海床土体对钢悬链线立管疲劳损伤的影响仅局限于触地段部分,对悬挂段及以上部分,几乎没有什么影响。
|
图 9 不同土体特性下触地点应力时程曲线 Fig. 9 Stress-history curves under different soil properties at TDP |

|
图 10 不同土体特征下悬挂点应力时程曲线 Fig. 10 Stress-history curves under different soil properties at suspension point |
钢悬链线立管在深海油气开采中发挥越来越重要的作用,在立管的设计过程中,对其所承受的实际载荷、立管悬垂段部分、与海床接触的触地段部分、海床土体等重要部位及参数应给予重点考虑,为钢悬链线立管的安全使用提供技术支撑。
| [1] |
黄维平, 李华军. 深水开发的新型立管系统:钢悬链线立管(SCR)[J]. 中国海洋大学学报 , 2006, 36 (5) :775–780.
HUANG Wei-ping, LI Hua-jun. A new type of deepwater riser in offshore oil & gas production:the steel catenary riser, SCR[J]. Periodical of Ocean University of China , 2006, 36 (5) :775–780. |
| [2] | AUBENY C P, BISCONTIN G. Seafloor-riser interaction model[J]. International Journal of Geomechanics , 2009, 9 (3) :133–141. DOI:10.1061/(ASCE)1532-3641(2009)9:3(133) |
| [3] | NAKHAEE A. Study of the fatigue life of steel catenary risers in interaction with the seabed[D]. Texas, USA:Texas A & M University, 2010:4-10. |
| [4] | NAKHAEE A, ZHANG J. Trenching effects on dynamic behavior of a steel catenary riser[J]. Ocean Engineering , 2010, 37 (2/3) :277–288. |
| [5] |
杜金新, LOWY M. 海洋立管-海床土体接触作用数值分析[J]. 工程地质计算应用 , 2008 (4) :6–11.
DU Jin-xin, LOW Y M. The numerical analysis of sea riser-seabed soil contact[J]. Engineering Geology Computer Application , 2008 (4) :6–11. |
| [6] |
杨和振, 李华军. 深海钢悬链立管时域疲劳寿命预估研究[J]. 振动与冲击 , 2010, 29 (3) :22–25.
YANG He-zhen, LI Hua-jun. Time domain fatigue life prediction for deepwater steel catenary riser[J]. Journal of Vibration and Shock , 2010, 29 (3) :22–25. |
| [7] |
傅俊杰, 杨和振. 深海钢悬链立管触地点动力响应分析[J]. 海洋工程 , 2009, 27 (2) :36–40, 45.
FU Jun-jie, YANG He-zhen. Dynamic response analysis of a deepwater steel catenary riser at the touchdown point[J]. The Ocean Engineering , 2009, 27 (2) :36–40, 45. |
| [8] | BRIDGE C, WILLS N. Steel catenary riser-results and conclusions from large scale simulations of seabed interaction[J]. UK:2H Offshore Engineering Ltd , 2002 :5–10. |
| [9] | AUBENY C P, BISCONTIN G, ZHANG J. Seafloor interaction with steel catenary risers[J]. Texas:Offshore Technology Research Center of Texas A & M University , 2006 :2–6. |
| [10] | 杨进, 刘书杰, 姜伟, 等. ANSYS在海洋石油工程中的应用[M]. 北京: 石油工业出版社, 2010 : 39 -45. |
| [11] | SPARKS C. Fundamentals of marine riser mechanics[M]. Tulsa: Penn Well Corporation, 2007 : 61 -75. |
| [12] | DUNLAP W A, BHOJANALA R P, MORRIS D V. Burial of vertically loaded offshore pipelines in weak sediments[C]//Proceedings of Offshore Technology Conference. Houston, Texas, USA:SPE, 1990:263-270. |
| [13] | BRIDGE C, LAVER K, CLUKEY E, et al. Steel catenary riser touchdown point vertical interaction models[C]//Proceedings of Offshore Technology Conference. Houston, Texas, USA:SPE, 2004:876-885. |
| [14] | DNV. Fatigue assessment of ship structures[R]. Hvik:DET Norske Veritas, 2003. |
| [15] | LEIPPER D F. A sequence of current patterns in the gulf of Mexico[J]. Journal of Geophysical Research , 1970, 75 (3) :637–657. DOI:10.1029/JC075i003p00637 |
| [16] | 黄祥鹿, 陆鑫森. 海洋工程流体力学及结构动力响应[M]. 上海: 上海交通大学出版社, 1992 : 81 -88. |
| [17] |
白兴兰, 黄维平, 高若沉. 海床土刚度对钢悬链线立管触底点动力响应分析的影响[J]. 工程力学 , 2011, 28 (S1) :211–216.
BAI Xing-lan, HUANG Wei-ping, GAO Ruo-chen. Effect of seabed soil stiffness on dynamic response of a steel catenary riser at touchdown point[J]. Engineering Mechanics , 2011, 28 (S1) :211–216. |
 2016, Vol. 38
2016, Vol. 38
