0 引言

鱼雷在纵向平面内的运动方程具有明显非线性，一般来说，研究鱼雷非线性问题需要对运动方程进行不断地简化和限制。通常将非线性微分方程线性化，然后按线性方程进行运动分析和控制器设计，实践证明多数情况下线性方法可行^[1]。但随着对鱼雷相关技术的研究不断深入，鱼雷运动中蕴涵的非线性因素越来越受到重视。如鱼雷纵向运动方程中所包含的流体动力系数都是通过试验测定，但随着作战使用环境以及鱼雷使用方式的不同，这些系数值会发生变化^[2]，甚至会导致鱼雷运动由稳态跳变到不稳态，现实中表现为跳水或沉底^[3]。因此，研究鱼雷在流体动力参数存在扰动时的运动稳定性，有利于改善鱼雷的运动特性，匹配鱼雷机动性与稳定性。近年来，对水下航行体运动稳定性的分叉研究工作已经展开。文献[5]和文献[6]以横舵角为分叉参数，分别对鱼雷和潜艇纵向运动的跨临界分叉进行研究；文献[7]以控制器参数为分叉参数，对鱼雷爬潜运动的跨临界分叉进行研究；文献[8]和文献[9]分别以控制器参数和空化数为分叉参数，对水下高速运动体纵向运动的Hopf分叉进行研究；文献[10]以流体动力参数为分叉参数，对鱼雷在非控状态下纵向运动的跨临界分叉和Hopf分叉进行研究；文献[11]对水下航行体的纵倾航行稳定性进行了研究分析。上述工作在研究属静态分叉的跨临界分叉时，都给出了系统的分叉范式；而研究属动态分叉的Hopf分叉时，却未给出系统的解析表达式，而是通过数值仿真证明了Hopf分叉的存在。

本文以目前常见的采用比例微分控制的鱼雷为研究对象，将鱼雷定深运动模型中所包含的某一流体动力参数的扰动作为分叉参数，利用中心流形定理推导出鱼雷定深运动各状态参量的解析表达式，对系统的Hopf分叉进行研究，并进行仿真验证。可揭示比例微分控制下，鱼雷定深运动失稳的本质原因，并完善鱼雷航行稳定性分析理论体系。

1 鱼雷定深运动方程

鱼雷定深运动方程由文献[1]给出：

$ \left\{ {\begin{array}{*{20}{l}} {\dot y = v\sin (\theta -\alpha )}\text{，} \\ {m\dot v = (B-mg)\sin (\theta -\alpha ) + T-D}\text{，} \\ {mv(\dot \theta -\dot \alpha ) = (B-mg)\cos (\theta -\alpha ) + T\alpha + L}\text{，}\\ {{J_z}{{\dot \omega }_{zB}} = N-B({Y_b}\sin \theta -{X_b}\cos \theta )-T{Y_T}\text{，}\quad \;} \\ {\dot \theta = \omega\!\!\!\!\!\!{\quad _{zB}}} \text{；} \end{array}} \right. $

(1)

将其化为如下标准形式^[1]：

$ \left\{ {\begin{aligned} & {\dot y = v\sin (\theta -\alpha )}\text{，} \\ & {\dot v = {k_{11}}{v^2} + {k_{14}}\sin (\theta -\alpha ) + {k_{18}}}\text{，}\\ & \dot \alpha \! = 1/v({k_{21}}{v^2}\alpha + {k_{22}}v{\omega _{zB}} + {k_{23}}\alpha +\\ & \quad \quad \!\! {k_{24}}\alpha \sin (\theta -\alpha ) + {k_{25}}\cos (\theta -\alpha )+ \\ & \quad \quad \!\! {k_{26}}\cos \theta + {k_{27}}\sin \theta + {k_{28}} + {k_{29}}{v^2}{\delta _e})\text{，}\\ & {{\dot \omega }_{zB}} = {k_{31}}{v^2}\alpha + {k_{32}}v{\omega _{zB}} + {k_{34}}\alpha \sin (\theta -\alpha )+ \\ & \quad \quad \, \, \, \, {k_{35}}\cos (\theta -\alpha ) + {k_{36}}\cos \theta + \\ & \quad \quad \, \, \, \, {k_{37}}\sin \theta + {k_{38}} + {k_{39}}{v^2}{\delta _e}\text{，}\\ & {\dot \theta = {\omega _{zB}}} \text{。} \end{aligned}} \right. $

(2)

式中：y为鱼雷航深；v为鱼雷速度；α，θ和Θ分别为攻角、俯仰角及弹道倾角；${\omega _{zB}}$为俯仰角速度；${\delta _e}$为横舵角；系数k_ij的定义可参见文献[1]，它们包含了鱼雷流体动力参数。方程右端为定深运动参数的非线性函数。鱼雷定深控制器采用如下经典比例微分控制规律^[1]：

$ {\delta _e} = {k_y}(y-{y_0}) + {k_\theta }(\theta -{\theta _0}) + {\delta _{e0}}\text{。} $

(3)

式中：y₀为设定航深；θ₀为平衡俯仰角；${\delta _{e0}}$为平衡舵角；k_y和k_θ为控制参数。

2 分叉分析

令$\tilde x = {[{\tilde x_1}, {\tilde x_2}, {\tilde x_3}, {\tilde x_4}, {\tilde x_5}]^{\rm T}} = {[y, v, \alpha, {\omega _{zB}}, \theta]^{\rm T}}$，由$\dot{\tilde{x}}={{[\dot{y},\dot{v},\dot{\alpha },{{{\dot{\omega }}}_{zB}},\dot{\theta }]}^{\text{T}}}=0$得到系统（2）的平衡态${\tilde x_0} = {[{y_0}, {v_0}, {\alpha _0}, {\omega _{zB}}_0, {\theta _0}]^{\rm T}}$。作变换$x = \tilde x-{\tilde x_0}$，选择鱼雷的升力因数对角速度${\omega _{zB}}$的旋转导数$C_y^{{\omega _z}}$为例进行研究，其试验量测值为$C_{y0}^{{\omega _z}} = 1.17$，设其受到一个扰动$\Delta m$的作用，则$C_y^{{\omega _z}} = C_{y0}^{{\omega _z}} + \Delta m$，将方程（2）改写成状态方程形式：

$ \dot x = G(x, \Delta m)\text{，} $

(4)

在平衡点处利用泰勒级数展开，我们可以得到新的系统：

$ \dot x = A(\Delta m)x + F(x, \Delta m)\text{，} $

(5)

式中：F(x, ∆m)为系统的高阶项；A(∆m)由下式可得：

$ A(\Delta m) = {\left. {\frac{{\partial {G_i}}}{{\partial {x_j}}}} \right|_{x = 0}}(i, j = 1, 2, 3, 4, 5)\text{，} $

(6)

以国外某型鱼雷为例，其总体和流体动力参数见文献[12]，设鱼雷以航速30 kn进行定深直航，将以上参数值代入式（4）和式（6）可得：

$ {\boldsymbol{A}} \!=\! \left[\!\! {\begin{array}{*{20}{c}} \! 0 &\! 0 &\! {-15.42} & \!0 & \!{15.42} \\ \! 0 &\! {-0.27} & \!{1.83} &\! 0 & \!{-1.83} \\ \!{-0.02} &\! {-0.01} & \!{-1.37} &\! {0.12-0.25\Delta m} &\! {-0.47} \\ \! {-0.40} & \!{0.01} & \!{11.16} &\! {-7.95 + 0.17\Delta m} & \!{-9.04} \\ \! 0 & \!0 &\! 0 & \!1 &\! 0 \end{array}} \!\!\right]\text{。} $

参考$C_{y0}^{{\omega _z}}$的值，将扰动∆m的取值范围设定为[-5,5]，利用非线性系统稳定性理论对A(∆m)的特征根进行分析可知^[13]：当-3.40 < ∆m≤5时，其特征值都有负实部，零解渐进稳定；当-5≤∆m < -3.40时，具有正实部的特征值，零解不稳定；当∆m=-3.40时，特征值为λ_{1, 2, 3, 4, 5}=-0.27, -9.02, -1.23i, -0.88, 1.23i，含有1对纯虚根，需用中心流形定理进行研究。

作线性变换y=p^-1x，p为${\left. {A(\Delta m)} \right|_{\Delta m = -3.40}}$所对应的特征向量所构成的矩阵，式（5）可化为：

$ \begin{gathered} \left[{\begin{array}{*{20}{c}} {{{\dot y}_1}} \\ {{{\dot y}_2}} \\ {{{\dot y}_3}} \\ {{{\dot y}_4}} \\ {{{\dot y}_5}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {-0.27} & {} & {} & {} & {} \\ {} & {-9.02} & {} & {} & {} \\ {} & {} & {-1.23i} & {} & {} \\ {} & {} & {} & {-0.88} & {} \\ {} & {} & {} & {} & {1.23i} \end{array}} \right]\text{×}\\ \left[{\begin{array}{*{20}{c}} {{y_1}} \\ {{y_2}} \\ {{y_3}} \\ {{y_4}} \\ {{y_5}} \end{array}} \right] + F'\left( {y, \Delta m} \right) \text{，} \quad \quad \quad \quad \quad \\ \end{gathered} $

(7)

式中$F'\left( {y, \Delta m} \right)$为系统的高阶项。根据中心流形定理可将上式化为：

$ \left\{ \begin{gathered} \dot v = \boldsymbol{B}v + \boldsymbol{M}(v, w) \hfill\text{，}\\ \dot w = \boldsymbol{C}w + \boldsymbol{N}(v, w) \hfill \text{。}\\ \end{gathered} \right. $

(8)

式中：B为2 × 2矩阵；C为3 × 3矩阵。它们分别对应A(∆m)的零实部和负实部特征值，可将其表示为：

$ w = h(v), \;h(0) = Dh\;(0) = 0 \text{。} $

令${h_i}({y_3}, {y_5}) = {a_i}y_3^2 + {b_i}y_5^2 + {c_i}{y_3}{y_5} + o\, (y_3^3, y_5^3)$(i=1, 2, 3)，代入式（8）并比较同阶系数可得：

$ \begin{gathered} {a_{1, 2, 3}} = -0.008-0.006i, 0.013 + 0.009i, - 0.002-0.021i \hfill\text{，} \\ {b_{1, 2, 3}} = -0.008 + 0.006i, 0.013-0.009i, - 0.002 + 0.021i \hfill\text{，} \\ {c_{1, 2, 3}} = -0.064, 0.098, - 0.034\text{。} \hfill \\ \end{gathered} $

从而进一步得到：

$ \begin{aligned} {{\dot y}_3} = & -1.234i{y_3} + (0.037 + 0.054i)y_3^2 + \\ & (0.007 + 0.003i)y_5^2 + (0.023 + 0.114i){y_3}{y_5}\text{，} \\ {{\dot y}_5} = & 1.234i{y_5} + (0.007-0.003i)y_3^2+ \\ & (0.037-0.054i)y_5^2 + (0.023-0.114i){y_3}{y_5}\text{。} \\ \end{aligned} $

(9)

经分析可知y₃和y₅是共轭复根，进行如下坐标变换：

$ {y_3} = r(\cos o + i\sin o), \;{y_5} = r(\cos o-i\sin o)\text{，} $

(10)

将式（10）代入式（9）整理可得：

$ \begin{aligned} \frac{1}{r} = & \frac{1}{{1.23}}(1 + 0.007\sin o{\cos ^2}o +\\ & 0.160{\sin ^2}o\cos o-0.021{\sin ^3}o + 0.171{\cos ^3}o)\text{，} \\ \end{aligned} $

(11)

相应地可求得x的表达式为：

$ \left\{ \begin{gathered} {x_1} = -2.84{r^2}{\cos ^2}o-1.69{r^2}{\sin ^2}o-5.18r\sin o +\\ 0.86{r^2}\sin o\cos o + 28.03r\cos o \text{，}\\ {x_2} = -0.35{r^2}{\cos ^2}o-0.20{r^2}{\sin ^2}o + 1.28r\sin o +\\ 0.11{r^2}\sin t\cos o-3.04r\cos o \text{，}\\ {x_3} = -0.11{r^2}{\cos ^2}o-0.07{r^2}{\sin ^2}o-0.88r\sin o +\\ 0.08{r^2}\sin o\cos o-1.69r\cos o \text{，}\\ {x_4} = 0.12{r^2}{\cos ^2}o + 0.10{r^2}{\sin ^2}o + 2.60r\sin o -\\ 0.36{r^2}\sin o\cos o-1.68r\cos o \text{，}\\ {x_5} = 0.06{r^2}{\cos ^2}o + 0.03{r^2}{\sin ^2}o-1.36r\sin o +\\ 0.02{r^2}\sin o\cos o-2.11r\cos o\text{。} \\ \end{gathered} \right. $

(12)

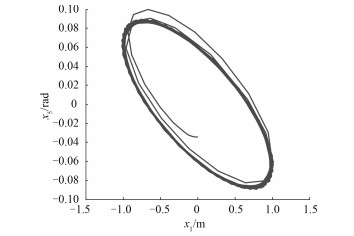
分析式（11）和式（12）可知，此时x=[x₁, x₂, x₃, x₄, x₅]^T是关于参量O的周期函数，系统从平衡点处产生极限环即发生Hopf分叉。Hopf分叉是动态分叉的典型形式, 指参数∆m经过分叉点时，系统的平衡点由渐近稳定的焦点变成不稳定焦点，并产生孤立周期运动的突变现象^[14]。

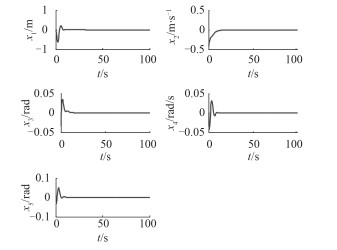
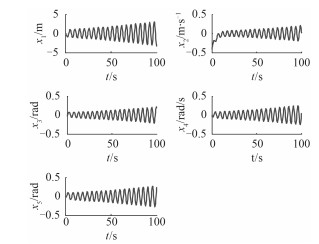
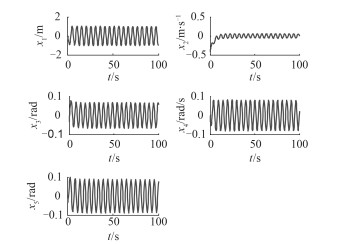
3 数值仿真

为了验证分叉分析结果，进行数值仿真。设鱼雷的初始速度为15 m/s，发射深度与设定航深相同，其他状态参量初始值都为0，选择不同的流体动力系数干扰值∆m，进行计算机仿真，图 1～图 3为式（4）在∆m取不同值时的状态响应曲线。

分析图 1～图 3可知，当$-3.40 < \Delta m \leqslant 5$（以∆m为例）时，x收敛于零点；当$-5 \leqslant \Delta m <-3.40$（以∆m为例）时，x发散；当∆m=-3.40时，x产生等幅振荡。由图 4可知，此时x中的任意2个状态变量（以x₁和x₅为例）在相图上构成极限环，说明了极限环与Hopf分叉的对应关系，仿真结果与理论分析结果相吻合。由此可知，流体动力参数的变化会导致鱼雷定深航行失稳。

4 结语

鱼雷定深运动方程中，含有各种非线性项和耦合项，为方便起见，在研究中经常对非线性的影响进行忽略和简化。分析非线性问题是鱼雷航行动力学与控制的研究分支之一，本文运用分叉理论处理鱼雷定深航行的非线性问题，该方法不需要过于简化方程，利用等价变换将高维系统约化到低维的包含了定深航行稳定性全部信息的中心流形上来进行研究。文中选择某一流体动力参数扰动值为分叉参数，推导出了状态变量的解析表达式，讨论鱼雷在定深航行中的Hopf分叉现象，并进行数值仿真验证。研究表明，流体动力系数变化会对鱼雷的定深航行稳定性产生影响，该结果可用来解释鱼雷发生跳水、沉底等现象的原因，同时也可为研究非线性因素影响下的鱼雷运动稳定性提供分析工具。