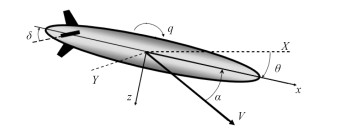
无人水下航行器(Unmanned Underwater Vehicle,UUV)自20世纪中期开始探索发展至今,其在海洋活动及军事中的作用和价值越来越受到海洋国家的高度重视。其中,以鱼雷型UUV为载体加装模块化的功能载荷,具备海洋环境调查、海战场情报搜集等任务的信息型UUV受到海洋国家尤其是海洋军事强国的重视[1-2],其典型的航行体外型如图 1所示。
|
图 1 鱼雷型UUV外型图 Fig. 1 TheeExternal configuration of torpedo type UUV |
鱼雷型信息UUV航行速度低,工作环境干扰多,流体动力学参数含有建模误差。由于其搭载的众多声、光学成像载荷对载体稳定姿态要求高,使得设计鱼雷型UUV的姿态控制系统成为一个难题。
本文针对鱼雷型UUV航行过程中外界干扰强烈问题,并同时考虑系统中的不确定性,提出一种由标称控制器、扰动估计器和补偿控制器构成的鲁棒控制器。在该鲁棒控制器中,避免了复杂控制率转换和大量的控制增益调节,就能保证控制系统具有好的鲁棒性。基于设计的控制器构型,标称控制器为PID控制器,扰动估计器为非线性状态观测器,其主要作用是对系统的不确定项和外界干扰组成的复合干扰项进行观测逼近。并合理设计补偿控制器以解决流体动力学参数和外界扰动大范围剧烈变化情况下的UUV航行姿态鲁棒控制问题。
1 鱼雷型UUV鲁棒控制器 1.1 鲁棒控制器的原理传统的鲁棒控制方法具有无法兼顾系统的性能和鲁棒性的缺陷,经过深入鱼雷型UUV航行特点和控制需求,设计主鲁棒控制器构型。该控制器可分为2部分,一是以跟踪误差为输入的主控制器,二是以观测误差为输入的补偿控制器。主控制器可用现有的控制理论设计,主要考虑系统的性能;补偿控制器主要考虑如何容忍各种不确定性和外部干扰,这意味着在鲁棒控制器构型下,系统性能和鲁棒性可以同时兼顾。
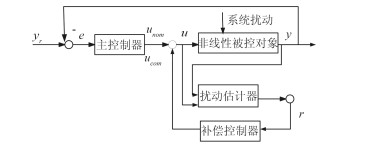
本文所设计的鲁棒控制器构型如图 2所示。
|
图 2 鲁棒控制器构型 Fig. 2 The configuration of robust controller |
由图 2可见,该鲁棒控制器由主控制器、扰动估计器和补偿控制器3个子模块构成。其中,主控制器以跟踪误差为输入,补偿控制器以扰动估计为输入,这里扰动包括系统不确定性、流体动力学参数偏离标称值的变化或UUV航行时外部环境的干扰。
当受控系统未受到扰动时,仅主控制器起作用,扰动估计器输出为0;当受控系统受到外界扰动或流体动力学参数偏离标称值时,扰动估计器对系统扰动进行实时估计并输出补偿调整信号,驱动补偿控制器工作来克服系统扰动对闭环控制系统性能、甚至闭环系统稳定性的影响。补偿控制作用可在保证系统稳定的同时,使整个受控系统具有较强的鲁棒性[3]。
1.2 鱼雷型UUV纵向鲁棒控制系统设计主控制器可采用现有成熟的控制方法来设计,本文采用PID控制器。通过选取航路上的平衡点,利用小扰动线性化方法得到鱼雷型UUV纵向线性化模型如下:
| $ \left\{ \begin{array}{l} {A_{11}}\ddot \theta {\rm{ + }}{A_{12}}\dot \theta {\rm{ + }}{A_{13}}\dot \alpha {\rm{ + }}{A_{14}}\alpha {\rm{ = }}{A_{15}}{\delta _e}\text{,}\\ {A_{21}}\ddot \theta {\rm{ + }}{A_{22}}\dot \theta {\rm{ + }}{A_{23}}\dot \alpha {\rm{ + }}{A_{24}}\alpha {\rm{ = }}{A_{25}}{\delta _e}\text{。} \end{array} \right. $ | (1) |
式中:
| $ \begin{array}{l} {A_{11}} = \left( {m{x_c} + {\lambda _{26}}} \right)/\frac{1}{2}\rho V_0^2S, {A_{21}} = \left( {{J_{zz}} + {\lambda _{66}}} \right)/\frac{1}{2}\rho V_0^2SL, \\ {A_{12}} = \left( {\mu - C_y^{{\omega _z}}} \right)L/{V_0}, \;\;\;\;\;\;\;{A_{22}} = \left( {\mu {x_c} - m_z^{{\omega _z}}} \right)L/{V_0}, \\ {A_{13}} = \left( {m + {\lambda _{22}}} \right)/\frac{1}{2}\rho V_0^2S, \;\;\;\;{A_{23}}{\rm{ = - }}\left( {m{x_c} + {\lambda _{26}}} \right)/\frac{1}{2}\rho V_0^2SL, \\ {A_{14}} = - C_y^{{\delta _e}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{A_{24}} = - m_z^\alpha, \\ {A_{15}} = C_y^{{\delta _e}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{A_{25}} = m_z^{{\delta _e}}。 \end{array} $ |
本文研究的鱼雷型UUV,口径210 mm,长度2.85 m,重量175 kg,表面积为2.114 m2,设计航速为2 kn,航深50 m。利用CFD计算其流体动力学参数并以此得到纵向传递函数如下:
| $ A(s) = \frac{{\alpha (s)}}{{{\delta _e}(s)}} = \frac{{ - s - 0.0000385}}{{{s^2} + 0.91s + 0.27}}\text{,} $ | (2) |
| $ Q(s) = \frac{{\theta (s)}}{{{\delta _e}(s)}} = \frac{{ - 1.84}}{{{s^2} + 0.91s + 0.27}}\text{,} $ | (3) |
| $ F(s) = \frac{{\alpha (s)}}{{q(s)}} = \frac{{A\left( s \right)}}{{sQ\left( s \right)}}\text{。} $ | (4) |
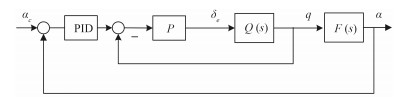
针对UUV航行特点,选取PID控制器结构如图 3所示。
|
图 3 纵向PID控制结构图 Fig. 3 The longitudinal PID controller |
对于补偿控制器的设计,主要研究基于NESO的扰动估计器设计和补偿控制器设计。
1.3 基于NESO的扰动估计器扩张状态观测器(Extended state observer, ESO)能够同时实现状态和干扰估计的一种应用广泛的观测器,其以输出误差为输入,即可以对受控对象的状态量进行估计,还可对受控系统的不确定性模型和外界环境扰动总和进行实时估计。按照其估计原理可以分为线性扩张状态观测器(Linear extended state observer, LESO)和非线性扩张状态观测器(Nonlinear extended state observer, NESO)2种[4]。
为了设计扰动估计器,针对于鱼雷型UUV纵向动力学模型,设计如下NESO[5-6]:
| $ \left\{ {\begin{array}{*{20}{c}} {e = {z_1} - y}\text{,}\\ {{{\dot z}_1} = {z_2} - {\beta _1}{f_{c1}}(e) + {f_1}(x) + {g_1}(x)u}\text{,}\\ {{{\dot z}_2} = {z_3} - {\beta _2}{f_{c2}}(e) + {f_2}(x) + {g_2}(x)u}\text{,}\\ {{{\dot z}_3} = - {\beta _3}{f_{c3}}(e)}\text{。} \end{array}} \right. $ | (5) |
其中,fc1(e)=e,
| $ {{f}_{c1}}\left( e \right)=e, \\ {f_{c2}}(e) = fal(e, {\alpha _2}, \delta ) = \left\{ \begin{array}{l} {\left| e \right|^{{\alpha _2}}}sign(e), {\rm{ }}\Phi \left| e \right| > \delta\text{,}\\ \left| e \right|/{\delta _2}^{1 - {\alpha _2}}, {\rm{ }}\Phi \left| e \right| \leqslant \delta\text{,} \end{array} \right.\\ {f_{c3}}(e) = fal(e, {\alpha _3}, \delta ) = \left\{ \begin{array}{l} {\left| e \right|^{{\alpha _3}}}sign(e), {\rm{ }}\Phi \left| e \right| > \delta\text{,}\\ \left| e \right|/{\delta _3}^{1 - {\alpha _3}}, {\rm{ }}\Phi \left| e \right| \leqslant \delta\text{。} \end{array} \right. $ | (6) |
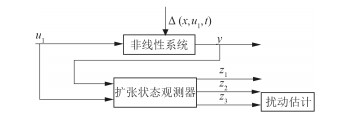
由上式可看出,扩张状态z3可以逼近鱼雷型UUV纵向模型中的干扰项△。
NESO的性能主要受到观测器设计参数
|
图 4 基于扩张状态观测器的扰动估计 Fig. 4 The disturbance estimation based on extended state observer |
根据扩张状态观测器的原理,下面以单变量系统为例说明其补偿控制器的设计方法和稳定性分析,扩张状态
| $ {u_{cf}}(t) = - {g_c}^{ - 1}(x){z_{n + 1}}\text{,} $ | (7) |
加入补偿控制律后,定义
| $ \dot x(t) = f(x) + g(x)\beta (x) + \xi\text{,} $ | (8) |
加入补偿控制律后的系统和二阶扩张状态观测器一起构成的整个闭环系统为:
| $ \left\{ \begin{array}{l} \dot x(t) = f(x) + g(x)\beta (x) + \xi \text{,}\\ {{\dot e}_1} = {e_2} - {\beta _1}{f_{c1}}({e_1})\text{,}\\ {{\dot e}_2} = v(t) - {\beta _2}{f_{c2}}({e_1})\text{。} \end{array} \right. $ | (9) |
其中,
| $ {{f}_{c1}}\left( e \right)={{e}_{1}}, \\ {f_{c2}}\left( {{e_1}} \right) = {f_a}l\left( {{e_1}, {\alpha _2}, \delta } \right) = \left\{ \begin{array}{l} {\left| {{e_1}} \right|^{{\alpha _2}}}{\rm{sign}}\left( {{e_1}} \right), 当\left| {{e_1}} \right| > \delta, \\ \left| {{e_1}} \right|/{\delta ^{1 - {\alpha _2}}}, 当\left| {{e_1}} \right| \le \delta 。 \end{array} \right. $ |
式中v(t)为假设的扩张状态的导数。
|
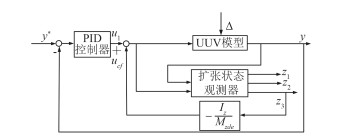
图 5 基于NESO的鲁棒控制系统 Fig. 5 robust control system based on NESO |
在本文设计的鲁棒控制构型下,当受控系统未受到外界环境干扰或者流体动力参数没有出现偏差的情况下,利用主控制器控制控制鱼雷型UUV是闭环稳定的且满足工程设计要求。若受控系统受到外界干扰或流体动力参数出现偏差,则NESO可对其进行估计,并通过补偿控制器输出的补偿控制信号进行补偿,即可保证在主控制器和补偿控制器共同作用下的系统闭环稳定,且具有较好的性能。
2 仿真验证将所设计的鲁棒控制器应用于鱼雷型UUV的纵向姿态控制问题。由于鱼雷型UUV流体动力学参数存在很大的不确定性。另外,由于利用CFD计算得到的流体动力学参数与真实流体动力学参数之间存在一定的偏差,流体动力学参数偏差会导致UUV动态特性的变化,所有这些不确定性和偏差可以归结为系统方程中的干扰项。为验证本文所设计的鲁棒控制器的控制特性。
首先,选取弹道上某特征点,针对小扰动线性化模型进行仿真,考察在控制器作用下实际攻角对指令攻角的跟踪效果。
1)特征点选取为航行深度100 m,航行速度8 kn。
2)根据PID控制器参数理论设计控制器参数,进行适当调整后,确立PID控制器参数为:
3)根据NESO理论给出的经验参数和实际仿真效果,确立NESO参数为:
4)根据补偿控制器设计过程,补偿控制律为:
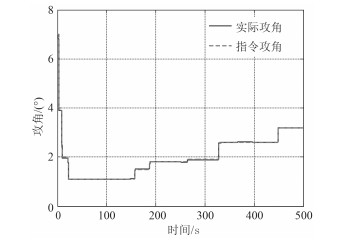
考虑到鱼雷型UUV在执行侦察任务时航行深度变化宽广,该区域流体参数存在很大的不确定性,基于目前的测试手段,很难得到精确值。另外,由于理论计算得到的流体动力参数与真实参数之间存在一定的偏差,而这些偏差会导致航行体动态特性的变化,因此引入75%的俯仰力矩系数偏差作为干扰输入,分别以PID和PID + NESO两种控制结构跟踪指令攻角,具体仿真结果如下图 6~图 9所示。
|
图 6 无干扰模型的PID控制跟踪效果 Fig. 6 PID control tracking effect without interference |
|
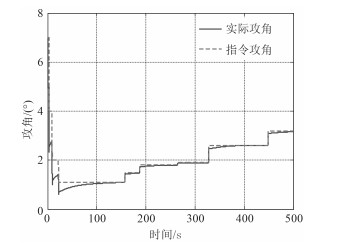
图 7 纵向力矩参数正向拉偏+外界干扰的PID控制跟踪效果 Fig. 7 PID control tracking effect of the longitudinal moment parameters of the positive bias + external disturbance |
|
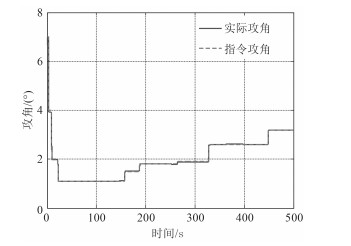
图 8 纵向力矩参数正向拉偏+外界干扰的PID + NESO控制跟踪效果 Fig. 8 PID +NESO control tracking effect of the longitudinal moment parameters of the positive bias + external disturbance |
|
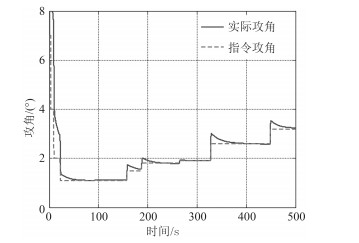
图 9 纵向力矩参数负向拉偏+外界干扰的PID控制跟踪效果 Fig. 9 PID control tracking effect of the longitudinal moment parameters of the negative bias + external disturbancess |
|
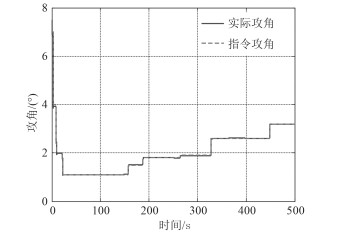
图 10 纵向力矩参数正向拉偏加外界干扰的PID + NESO控制跟踪效果 Fig. 10 PID +NESO control tracking effect of the longitudinal moment parameters of the negative bias + external disturbance |
由图 3~图 5可见,如果仅采用PID控制器,由于俯仰力矩系数偏差和外加干扰的影响,在整个仿真航行过程中,实际攻角对指令攻角的跟踪效果有一定误差;而采用PID + NESO控制器仍然具有较好的跟踪效果。这说明PID + NESO控制器克服了参数偏差所带来的影响,具有较强的鲁棒性。
3 结语本文通过分析鱼雷型UUV进行侦察任务时的航行特点,对航行控制的特点及不确定性进行简化处理。设计鲁棒控制器构型。在此构型的基础上,设计以跟踪误差为输入的控制器,以及以观测误差为输入的补偿控制器,对控制量进行计算和补偿。
根据鱼雷型UUV航行所需控制器的特点,采用扩张状态观测器来估计流体动力学参数变化及外部干扰所形成的不确定性。在应用扩张观测器的基础上,设计补偿控制器,对系统及外界环境产生的不确定性进行补偿。将补偿控制器与设计的控制系统的主控制器按照控制系统结构图进行结合,共同构成了鱼雷型UUV的鲁棒控制器。
| [1] |
陈强, 张林根. 美国军用UUV现状及发展趋势分析[J]. 舰船科学技术 , 2010, 32 (7) :129–134.
CHEN Qiang, ZHANG Lin-gen. Analysis of current situational development trend of US military UUV[J]. Ship Science and Technology , 2010, 32 (7) :129–134. |
| [2] |
胡红波, 宋涛. UUV在水下态势感知中的应用[J]. 水雷战与舰船防护 , 2013, 21 (4) :57–61.
HU Hong-bo, SONG Tao. The application of UUV in underwater situation awareness[J]. Mine Warfare & Ship Self-defence , 2013, 21 (4) :57–61. |
| [3] | ZHOU K M, REN Z. A new controller architecture for high performance, robust, and fault-tolerant Control[J]. IEEE Transactions on Automatic Control , 2001, 46 (10) :1613–1618. DOI:10.1109/9.956059 |
| [4] | 朱芳来.非线性控制系统观测器研究[D].上海:上海交通大学, 2001. |
| [5] | HAN Jing-qing. Active disturbance rejection control technique[M]. Beijing: National Defence Industry Press, 2008 . |
| [6] |
黄一, 韩京清. 非线性连续二阶扩张状态观测器的分析与设计[J]. 科学通报 , 2000, 45 (21) :1938–1944.
HUANG Yi, HAN Jing-qing. Analysis and design for the second order nonlinear continuous extended states observer[J]. Chinese Science Bulletin , 2000, 45 (21) :1938–1944. DOI:10.1007/BF02909682 |
| [7] | HUANG Y, XU K K, HAN J Q. Application of ADRC for aircraft attitude control[C]//Proceedings of the 3rd Asian Control Conference. Shanghai:ASCC, 2000. |
| [8] |
秦昌茂, 齐乃明, 朱凯. 高超声速飞行器自抗扰姿态控制器设计[J]. 系统工程与电子技术 , 2011, 33 (7) :1607–1610.
QIN Chang-mao, QI Nai-ming, ZHU Kai. Active disturbance rejection attitude control design for hypersonic vehicle[J]. Systems Engineering and Electronics , 2011, 33 (7) :1607–1610. |
 2016, Vol. 38
2016, Vol. 38
