滤波的目的是提取信号中的有用信息,如频率特征、时间特征等,便于对信号进行分析使用[1]。传统的滤波方法大都以线性高斯平稳信号为研究对象,但现实中大多数信号都是非线性非平稳的,利用这些方法滤波难以获得理想的效果[2]。因此现代滤波方法主要集中于对非线性非平稳信号的分析研究上,如短时傅里叶变换法、Gabor展开法、Wigner-Vill分布法及小波变换法[3-6]等,但这些方法存在着时频窗口无法自适应调整、对多分量信号会产生交叉项、受到小波基以及Heisenberg不确定原理的限制等问题[7-9]。
经验模态分解(EMD)方法是一种自适应信号时频处理方法,它能够根据信号本身的特性自适应地产生固有模态函数(IMF),这些IMF能很好地反映信号在任何时间局部的频率特征[10]。将EMD方法与小波阈值方法结合起来在低频信号滤波方面已取得了不错的效果[2, 11]。但对于中高频信号,由于信号与噪声可能同时集中于某一个或某几个模态中,若沿用此滤波方法,则可能会损失大量的有用信号,无法获得令人满意的效果。因此本文提出一种适用于中高频信号的滤波方法,并采用数值仿真方法找到不同频段信号理想的滤波方法,从而给出全频段水声信号的滤波方法。
1 基于EMD的小波阈值滤波方法 1.1 EMD分解方法EMD方法将信号分解成若干个频率从高至低的IMF,每个IMF可以看作是对原信号进行带通滤波的结果[12],它与传统固定截止频率滤波方法的不同之处在于,其通带截止频率自动随输入信号的变化而变化,因此可将其看作是自适应滤波器。采用EMD方法对信号进行处理后,若简单的将相应的几个IMF相加进行信号重构,只是粗糙的一种滤波方法,不会得到理想的滤波效果,因此需要进行进一步的滤波处理。
1.2 小波软阈值滤波方法由于经EMD处理后,得到的各IMF都是平稳的单分量信号,这类信号很适合采用小波阈值法进行滤波降噪[13]。小波软阈值滤波方法可用下式表达:
| $ \mathop {\mathop Y\limits^ \frown }\nolimits_j (i) = \left\{ \begin{array}{l} sign({Y_j}(i))(\left| {{Y_j}(i)} \right| - {t_j}), \begin{array}{*{20}{c}}\!\!\!\!\!\!\!\! {} & {\left| {{Y_j}(i)} \right|} \end{array} \geqslant {t_j}\text{,}\\[10pt] 0, \begin{array}{*{20}{c}} {} & {} & {} & {\begin{array}{*{20}{c}} {} & {} & {\begin{array}{*{20}{c}} {} & {\begin{array}{*{20}{c}} {} & \;\;\;\;\;\;\;\;\;\;\;\, \!\!\!\! \!\!\!\! {\left| {{Y_j}(i)} \right|} \end{array} < {t_j}}\text{。} \end{array}} \end{array}} \end{array} \end{array} \right. $ | (1) |
式中:第j层的阈值为
EMD方法从提出至今还不到20年,其理论上还不够成熟,因此在应用上还存在着一些问题,如端点效应、模态混叠等[14-15],为此许多学者提出了一系列改进方法,其中Huang等提出了一种新的噪声辅助数据分析方法——总体平均经验模式分解方法,即EEMD方法[16],该方法利用白噪声频谱均衡分布的特点来均衡噪声的特性,较为理想地解决了模态混叠等问题。
2.2 一种改进的基于EEMD的小波软阈值滤波方法经分析可知,如果对信号分解后得到的IMF直接在时域上进行滤波处理,会损失大量的中高频信号,若将各IMF转换至频域,利用信号频率与噪声频率相比较为集中的特点,在频域上利用小波软阈值滤波方法对相关模态进行处理,便能有效去除噪声,最后将这些模态组合起来进行信号重构,将会获得好的滤波降噪效果。基于以上分析,本文针对中高频信号,提出一种新的滤波方法,具体步骤如下:
1)对接收信号进行带通滤波处理,去除与有用信号频率相差较大的噪声;
2)对带通后的信号进行EEMD分解,得到一组IMF,并对各IMF进行FFT变换;
3)分析各IMF的频谱特性,选取信号主体所在的IMF,即体现信号频谱特性的IMF,利用类似于小波软阈值的方法对这些IMF进行降噪,得到降噪后的IMF';
4)将IMF'组合起来进行信号重构,再变换为时域信号,即得到滤波降噪后的信号。
这里,频域上的小波降噪软阈值函数为:
| $ IM{F'_k}(i) \!=\! \left\{ \begin{array}{l} IM{F_k}(i) \!-\! {d_k}(i), \!\!\!\!\!\!\begin{array}{*{20}{c}} {} & {\left| {IM{F_k}(i)} \right|} \end{array} \geqslant {C_k}\text{,}\\ 0, \begin{array}{*{20}{c}} {} & {} & {} & {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}}\!\!\!\!\!\!\!\! {} & {} \end{array}} & \; {\left| {IM{F_k}(i)} \right|} \end{array} < {C_k}}\text{。} \end{array} \end{array} \right. $ | (2) |
其中Ck为IMFk幅度的阈值,由于IMFk(i)都为复数信号,滤波只是对各元素的幅度进行处理,滤波后它们的相位信息应予以保留,因此dk(i)由下式计算:
| $ {d_k}\left( i \right) = {C_k}\left( {\cos {\theta _k}\left( i \right) + j\sin {\theta _k}\left( i \right)} \right)\text{。} $ | (3) |
其中
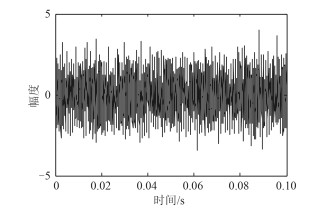
以频率为1 kHz、幅度为1的CW信号为例,当输入信噪比为-1 dB时,采用本方法对其滤波,图 1为滤波前信号波形图。
|
图 1 滤波前1 kHz CW信号波形(输入信噪比-1 dB) Fig. 1 The input waveform of 1 kHz CWsignal before filtered (input SNR=-1 dB) |
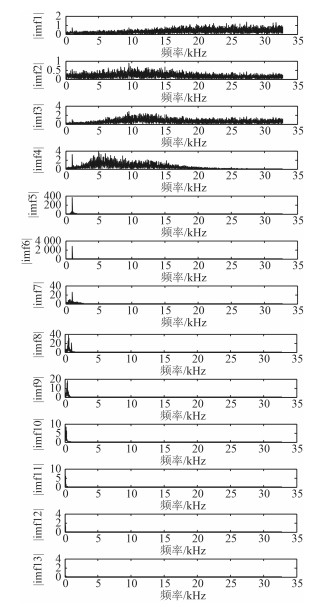
将信号进行带通滤波后,进行EEMD分解得到各IMF分量,再将各IMF分量进行FFT变换,得到其频域信号imf,所得频谱如图 2所示。由图 2可知,imf5和imf6中1 kHz信号的频谱幅度最强,将其他模态在频域上用小波阈值法进行滤波后,再与这2个模态组合起来并转换至时域,所得信号的输出信噪比为14.30 dB,与加噪前纯信号的相关系数为0.97。
|
图 2 各IMF分量频谱图 Fig. 2 The frequency spectrum of all IMFs |
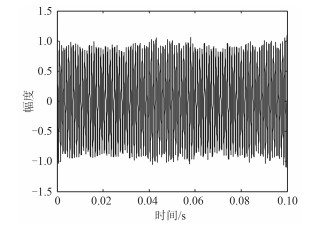
但在实际应用中,信号的实际频率并不能提前获知,噪声存在于各个模态中,因此可将所有模态进行滤波后,再组合起来进行重构。经计算可知,此时输出信噪比为15.13 dB,滤波后信号与加噪前纯信号的相关系数为0.99,所得信号波形如图 3所示。由此可知,将所有模态进行滤波后重构信号同样可以获得满意的效果。
|
图 3 滤波后频率1 kHz CW信号的输出波形 Fig. 3 The output waveform of 1 kHz CW signal after filtered |
以上提出一种适用于中高频信号的滤波方法,而文献[2]提出的方法对低频信号有良好的滤波效果。通过数字仿真的方法,研究这2种方法对不同频率信号的滤波效果,以获得对不同频率信号的理想滤波方法。
3 数值仿真验证由于水声信号形式一般为CW信号和LFM信号,下面就以这2种信号为例,分别采用以上2种方法进行滤波,然后对滤波效果进行分析。
3.1 CW信号仿真验证采用如下CW信号:
| $ x\left( t \right) = \cos \left( {2\pi {f_0}t} \right)\text{,} $ | (4) |
信号采样率为65 536 Hz,时长为0.1 s,加入高斯白噪声,分别采用原方法和新方法进行滤波,滤波效果用输出信噪比以及滤波后信号与加噪前纯信号的相关系数来衡量,信噪比采用工程中常用的计算方法[2]:
| $ SNR = 10\log \left( {\frac{{\sigma _x^2}}{{\sigma _n^2}}} \right)\text{。} $ | (5) |
式中:σx为加噪前纯信号x(t)的标准差;σn为信号y(t)中所包含噪声n(t)的标准差,n(t)=y(t)-x(t)。
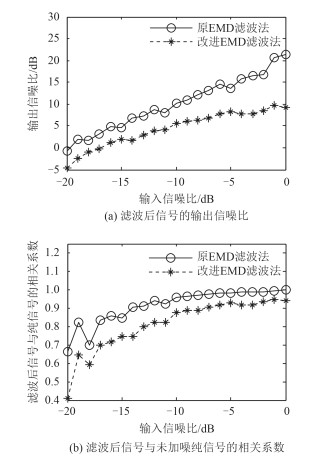
不同信号频率下,2种方法滤波后信号的输出信噪比随输入信噪比的变化曲线以及滤波后信号与加噪前纯信号的相关系数随输入信噪比的变化曲线如图 4~图 7所示。
|
图 4 对频率为100 Hz CW信号的滤波效果对比图 Fig. 4 The filtering results of two methods when the CW input signal frequency is 100 Hz |
|
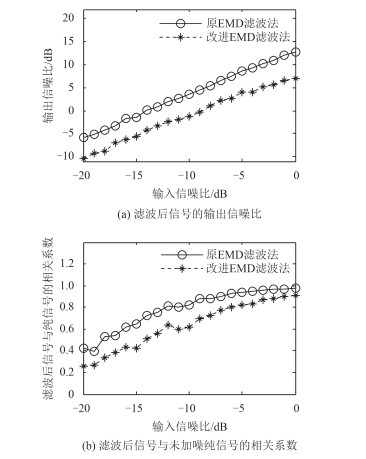
图 5 对频率为800 Hz CW信号的滤波效果对比图 Fig. 5 The filtering results of two methods when the CW input signal frequency is 800 Hz |
|
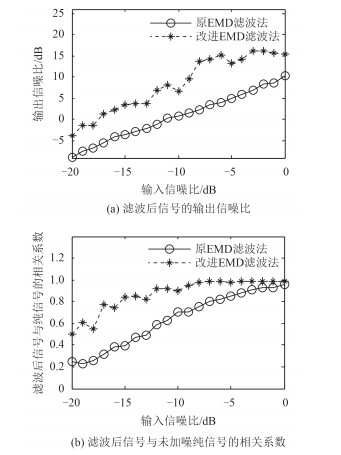
图 6 对频率为1 kHz CW信号的滤波效果对比图 Fig. 6 The filtering results of two methods when the CW input signal frequency is 1 kHz |
|
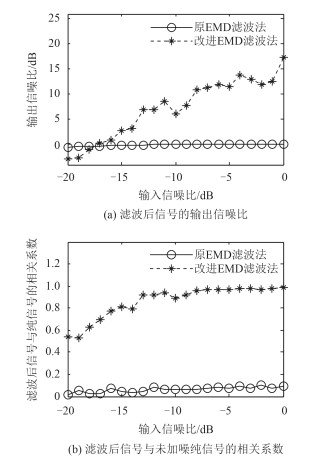
图 7 对频率为10 kHz CW信号的滤波效果对比图 Fig. 7 The filtering results of two methods when the CW input signal frequency is 10 kHz |
CW信号频率为100 Hz时,2种方法的输出信噪比和相关系数随输入信噪比的增加呈增大趋势,且原方法滤波效果优于改进方法,原方法输出信噪比最小为-0.74 dB,最大为21.34 dB,滤波后信号与加噪前纯信号相关系数最小为0.66,最大为0.99;改进方法输出信噪比最小为-4.73 dB,最大为9.61 dB,滤波后信号与加噪前纯信号相关系数最小为0.41,最大为0.94。相同输入信噪比下,原方法的输出信噪比改进方法最大提高12.23 dB;相关系数最大提高0.26。
CW信号频率为800 Hz时,2种方法的输出信噪比和相关系数随输入信噪比的增加呈增大趋势,且原方法滤波效果都优于改进方法,原方法输出信噪比最小为-5.86 dB,最大为12.73 dB,滤波后信号与加噪前纯信号相关系数最小为0.42,最大为0.97;改进方法输出信噪比最小为-10.33 dB,最大为7.05 dB,滤波后信号与加噪前纯信号相关系数最小为0.26,最大为0.91。相同输入信噪比下,原方法的输出信噪比改进方法最大提高5.68 dB;相关系数最大提高0.22。
CW信号频率为1 kHz时,2种方法的输出信噪比和相关系数随输入信噪比的增加呈增大趋势,且改进方法滤波效果都优于原方法,原方法输出信噪比最小为-8.78 dB,最大为10.20 dB,滤波后信号与加噪前纯信号相关系数最小为0.25,最大为0.95;改进方法输出信噪比最小为-3.73 dB,最大为16.26 dB,滤波后信号与加噪前纯信号相关系数最小为0.50,最大为0.99。相同输入信噪比下,原方法的输出信噪比改进方法最大提高11.42 dB;相关系数最大提高0.46。
CW信号频率为10 kHz时,对不同信噪比的输入信号,原方法的滤波效果基本保持不变,输出信噪比和相关系数都维持在0左右,说明此情况下,原滤波方法已失效;而改进方法的输出信噪比和相关系数随输入信噪比的增加呈增大趋势。改进方法输出信噪比最小为-2.89 dB,最大为17.44 dB,滤波后信号与加噪前纯信号相关系数最小为0.54,最大为0.99;相同输入信噪比下,改进方法的输出信噪比原方法最大提高17.41 dB,相关系数最大提高0.90。
3.2 LFM信号仿真验证采用如下LFM信号:
| $ x(t) = \cos \left[{2\pi \left( {{f_0} + \frac{b}{2}t} \right)t} \right]\text{。} $ | (6) |
式中:f0为信号起始频率;b=2 000 s-2。仿真其他参数设置与CW信号相同,本方法与原方法在不同输入信噪比条件下的滤波效果分别如图 8~图 11所示。
|
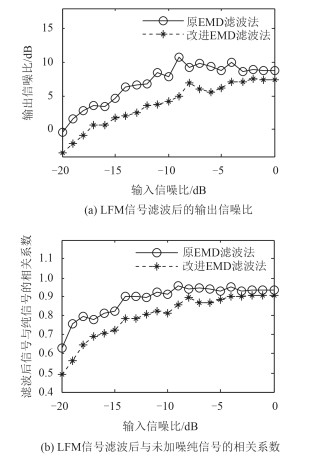
图 8 对起始频率为10 Hz LFM信号的滤波效果对比图 Fig. 8 The filtering results of two methods when the LFM input signal initial frequency is 10 Hz |
|
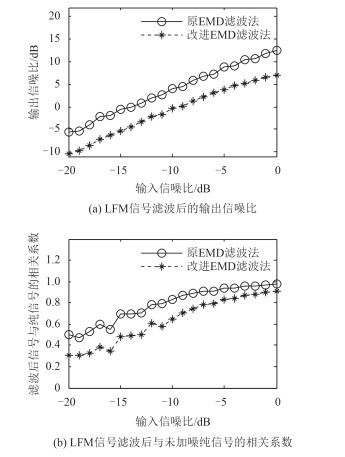
图 9 对起始频率为700 Hz LFM信号的滤波效果对比图 Fig. 9 The filtering results of two methods when the LFM input signal initial frequency is 700 Hz |
|
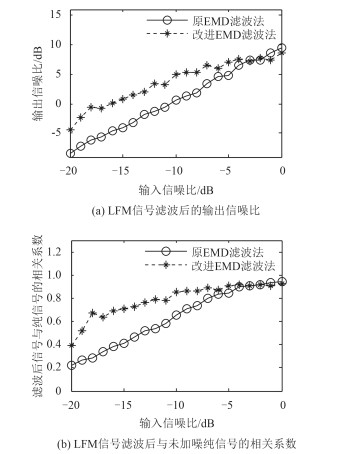
图 10 对起始频率为900 Hz LFM信号的滤波效果对比图 Fig. 10 The filtering results of two methods when the LFM input signal initial frequency is 900 Hz |
|
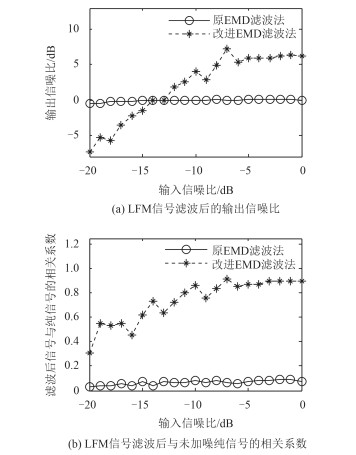
图 11 对起始频率为10 kHz LFM信号的滤波效果对比图 Fig. 11 The filtering results of two methods when the LFM input signal initial frequency is 10 kHz |
经分析可知,LFM信号起始频率为10 Hz时,2种方法的输出信噪比和相关系数随输入信噪比的增加呈增大趋势,且原方法滤波效果优于改进方法,原方法输出信噪比最小为-0.44 dB,最大为10.01 dB,滤波后信号与加噪前纯信号相关系数最小为0.63,最大为0.96;改进方法输出信噪比最小为-3.45 dB,最大为7.46 dB,滤波后信号与加噪前纯信号相关系数最小为0.49,最大为0.91。相同输入信噪比下,原方法的输出信噪比改进方法最大提高5.68 dB;相关系数最大提高0.19。
LFM信号起始频率为700 Hz时,2种方法的输出信噪比和相关系数随输入信噪比的增加呈增大趋势,且原方法滤波效果优于改进方法,原方法输出信噪比最小为-8.98 dB,最大为9.92 dB,滤波后信号与加噪前纯信号相关系数最小为0.27,最大为0.95;改进方法输出信噪比最小为-4.02 dB,最大为8.75 dB,滤波后信号与加噪前纯信号相关系数最小为0.49,最大为0.93。相同输入信噪比下,原方法的输出信噪比改进方法最大提高5.52 dB;相关系数最大提高0.29。
当LFM信号起始频率为900 Hz时,2种方法的输出信噪比和相关系数随输入信噪比的增加呈增大趋势。当输入信噪比小于-3 dB时,改进方法滤波效果优于原方法,原方法输出信噪比最小为-8.32 dB,最大为6.49 dB,滤波后信号与加噪前纯信号相关系数最小为0.22,最大为0.90;改进方法输出信噪比最小为-4.33 dB,最大为7.56 dB,滤波后信号与加噪前纯信号相关系数最小为0.39,最大为0.91。相同输入信噪比下,原方法的输出信噪比改进方法最大提高5.60 dB,相关系数最大提高0.39。随信号输入信噪比的增大,两种方法滤波效果的差异逐渐减小。当输入信噪比大于等于-3 dB时,原方法滤波效果略优于改进方法,原方法输出信噪比最小为7.39 dB,最大为9.45 dB,滤波后信号与加噪前纯信号相关系数最小为0.91,最大为0.94;改进方法输出信噪比最小为7.29 dB,最大为8.54 dB,滤波后信号与加噪前纯信号相关系数最小为0.91,最大为0.93。相同输入信噪比下,原方法的输出信噪比改进方法最大提高1.21 dB,相关系数最大提高0.02。
当LFM信号起始频率为10 kHz时,对不同信噪比的输入信号,原方法的滤波效果基本保持不变,输出信噪比和相关系数都维持在0左右,说明此情况下,原滤波方法已失效;而改进方法的输出信噪比和相关系数随输入信噪比的增加呈增大趋势。改进方法输出信噪比最小为-7.28 dB,最大为7.18 dB,滤波后信号与加噪前纯信号相关系数最小为0.30,最大为0.92;相同输入信噪比下,改进方法的输出信噪比原方法最大提高7.76 dB,相关系数最大提高0.86。
由此可知,不论是CW信号还是LFM信号,输入信噪比从-20 dB变化至0 dB时,当信号频率小于800 Hz时,原方法的滤波效果要优于改进方法,而当信号频率大于800 Hz时,改进方法的滤波效果优于原方法或两种方法滤波效果相近。因此在实际使用中,应首先对信号的所在频域进行预判,当信号频率为小于800 Hz的低频信号时,应采用原滤波方法,而当信号频率为大于800 Hz的中高频信号时,应采用本文提出的方法进行滤波。
4 结语本文提出了一种适用于中高频水声信号的滤波方法,首先将信号进行带通滤波,再采用EEMD方法对信号进行处理,将分解得到的各IMF转换为频域信号,然后选取相应模态采用小波软阈值方法对其进行滤波降噪,最后对信号进行重构,并将其转换为时域信号。在此基础上,分别采用本方法和原方法对不同频率的CW信号和LFM信号进行滤波,对仿真结果分析可知,当信号频率小于800 Hz时,采用原方法可获得较为理想的滤波效果;当信号频率大于800 Hz时,采用改进方法可获得令人满意的滤波效果。
| [1] | 孙晖.经验模态分解理论与应用研究[D].杭州:浙江大学, 2005. |
| [2] | 王婷. EMD算法研究及其在信号去噪中的应用[D].哈尔滨:哈尔滨工程大学, 2010. http://www.oalib.com/references/16081789 |
| [3] | 谢胜利, 何昭水, 高鹰. 信号处理的自适应理论[M]. 北京: 科学出版社, 2006 . |
| [4] | 张光明, 申永军, 吴彦彦. 基于Gabor变换的信号降噪方法[J]. 石家庄铁道学院学报(自然科学版) , 2009, 22 (3) :86–90. |
| [5] | 杨晓斌, 李海涛. Wigner-Vill分布在舰船调制特征提取中的应用研究[J]. 声学与电子工程 , 2012 (2) :14–16. |
| [6] | 余秋星, 符新伟, 李志舜. 基于小波变换的主动水声信号检测[J]. 声学技术 , 2003, 22 (2) :102–104. |
| [7] | 刘盛.自适应时频分析研究与发展[D].南昌:南昌航空大学, 2011. |
| [8] | 韩中合, 朱霄珣, 李文华, 等. 基于EMD消除Wigner-vill分布交叉项的研究[J]. 汽轮机技术 , 2010, 52 (3) :211–214. |
| [9] | 郑钧, 侯锐锋. 小波去噪中小波基的选择[J]. 沈阳大学学报 , 2009, 21 (2) :108–110. |
| [10] | 毛玉龙, 范虹. 经验模式分解回顾与展望[J]. 计算机工程与科学 , 2014, 36 (1) :155–162. |
| [11] | 江力, 李长云. 基于经验模分解的小波阈值滤波方法研究[J]. 信号处理 , 2005, 21 (6) :659–662. |
| [12] | QI K Y, HE Z J, ZI Y Y. Cosine window-based boundary processing method for EMD and its application in rubbing fault diagnosis[J]. Mechanical Systems and Signal Processing , 2007, 21 (7) :2750–2760. DOI:10.1016/j.ymssp.2007.04.007 |
| [13] | DONOHO D L, JOHNSTONE J M. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika , 1994, 81 (3) :425–455. DOI:10.1093/biomet/81.3.425 |
| [14] | HE Z, SHEN Y, WANG Q. Boundary extension for Hilbert-Huang transform inspired by gray prediction model[J]. Signal Processing , 2012, 92 (3) :685–697. DOI:10.1016/j.sigpro.2011.09.010 |
| [15] | WU Z H, HUANG N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis , 2009, 1 (1) :1–41. DOI:10.1142/S1793536909000047 |
| [16] | WU Z H, HUANG N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society a:Mathematical, Physical and Engineering Sciences , 2004, 460 (2046) :1597–1611. DOI:10.1098/rspa.2003.1221 |
 2016, Vol. 38
2016, Vol. 38
