船用燃机、航改燃机等大型船用低压涡轮的出口马赫数处于0.6~0.8,在叶顶处马赫数可能会达到0.9甚至超音速。为了获得叶型相关流场数据,通常情况下为了节省试验费用和获得更大的空间分辨率,需要把叶片放大后放到低速风洞中进行吹风试验,这样就需要保证叶片放大在低速风洞中获得的流场数据与高速时相同。在对叶片进行模化放大重新设计时,最主要的考虑在于高速和低速流体压缩性不同[1-2]。
Michele Marconcini等[3]研究了具有高升力系数的低压涡轮叶片的低速平面叶栅试验,他们通过修改叶型来匹配在中径位置处的压力系数Cp的分布,等熵速度系数分布,以及等熵马赫数Mais的分布,通过保证动力相似在相同雷诺数下的分布,来研究平面叶栅的性能。ZHANG Xue-feng等[4-5]研究了HSU2叶型在高速和低速2种状态下叶片的转捩和分离,具体研究了表面粗糙度和非稳态效应,重新设计的叶型主要匹配无量纲等熵马赫数的分布。Michael J. Brear等[6]对平面叶栅中叶顶泄漏流与压力面气动分离的相互影响进行了相关研究,这种干涉作用会对二次流的强度以及叶型损失有很大影响。GONZÁLEZ P.等[7-8]研究了低压涡轮叶片的压力面和吸力面的叶型损失,同样在低速风洞进行实验。
本文的主要研究目的是定义平面叶栅高低速叶顶间隙流动的差异性。首先采用改进全局优化遗传算法,对T106A进行再设计匹配高低速二维情况下的载荷分布,然后进行带叶顶间隙的三维计算分析由于叶顶间隙造成的不同,给出匹配叶顶间隙泄漏流的相关探讨。
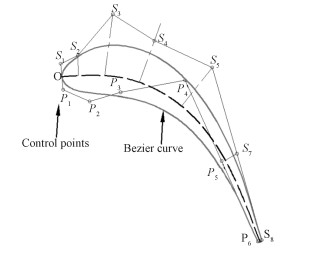
1 叶型参数化及最优化目标函数 1.1 叶片参数化在叶轮机械设计中,保持叶型几何的连续可导是非常重要的,否则叶型的效率、损失等各种设计参数都达不到要求,同时在设计中需要对叶型进行反复修改,需要用较少的参数就能够达到对叶型的控制。本文采用贝塞尔曲线来参数化涡轮叶片叶型,将叶型划分为尾缘、压力面、吸力面三部分分别造型,压力面和吸力面分别采用7次和9次贝塞尔曲线,尾缘采用圆弧设计,如图 1所示。
|
图 1 叶型参数化 Fig. 1 The parameterization of the blade airfoil |
贝塞尔曲线的数学表达式定义为:在空间给定n + 1个点P0,P1,…,Pn,定义下列参数曲线为n次Bezier曲线。
| $ \begin{array}{*{20}{l}} {B(t) = \sum\limits_{i = 0}^n {{P_i}} {b_{i, n}}(t), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in [0, 1]{\rm{, }}}\\ {{b_{i, n}}(t) = C_n^i{t^i}{{(1 -t)}^{n -i}}, \;\;\;\;\;\;\;i = 0, 1, ...n} \end{array}。 $ |
式中:Pi为各顶点的位置向量,bi, n为n阶伯恩斯坦多项式;折线P0,P1,…,Pn是曲线P(t)的控制多边形,从而确定唯一的贝塞尔曲线。
为保证叶型在前缘和尾缘平滑过渡,固定前缘点O以及S1和P1点,同时固定尾缘附近P6和S8两点。在进行叶型调整时,控制点S2~S7以及P2~P5只能沿垂直于原始叶型中弧线的方向进行,减少一个自由度即沿着图中的蓝色线进行移动,给定调整幅度为原始距离dc的±10%。通过上述叶片参数化过程,可以用9个参数来确定叶型,其中压力面4个,吸力面5个。
1.2 目标函数结合本文研究内容,最终要匹配叶片表面的压力系数分布,考虑到不同叶型参数沿弧长的分布,定义目标函数为
| $ f = \int_0^1 {\left( {\left| {Cp_{ps}^{ob}-C{p_{ps}}} \right| + \left| {Cp_{ss}^{ob}-C{p_{ss}}} \right|} \right){\rm{d}}s} $ |
以原始叶型控制点所在位置为初始位置,给定每个控制点的移动范围dc为-10%~10%。故有目标的最优化问题可简化为:
| $ \begin{array}{*{20}{c}} {{\rm{min}}} &{f;}\\ {{\rm{s}}.{\rm{t}}:}&{0.1 < {d_c}\left( i \right) < 0.1, i为控制点。} \end{array} $ |
选取T106A涡轮叶片作为研究对象,T106A涡轮叶片是典型的后载荷升力叶片,被广泛地应用于试验和数值研究,剑桥大学实验室获得了其原始叶型在低速风洞中试验数据,本文选用其作为代表进行研究具有一般性。表 1是T106A叶栅的相关几何数据,叶顶间隙为2%。
|
|
表 1 T106A平面叶栅几何参数 Tab.1 Characteristic dimensions of T106A cascade |
为验证数值计算湍流模型以及边界条件的准确性,将原始叶型低速数值计算的结果与低速试验结果进行对比验证。由于风洞吹风试验是T106A原始叶型直接在低速风洞的试验结果,故验证数值模拟采用三维低速计算。数值计算网格划分采用ICEM软件,图 2是网格示意图。计算采用了3组网格进行网格无关性验证,分别为300万、500万和600万网格,通过对比叶片中径位置叶片表面的压力系数分布,600万网格对比于500网格叶片表面静压分布变化不大,最终确定为500万网格。i,j,k分别为横向、展向和轴向的网格点数,i × j × k=99 × 106 × 293。叶片周围以及叶顶间隙布置O型网格,分别布置13和46层网格节点,在叶顶间隙区域k方向布置46个网格节点,整个叶片表面和上下端壁壁面y +均小于1。

|
图 2 网格示意图 Fig. 2 The Grid |
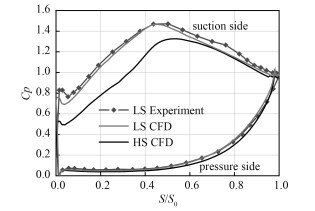
数值计算采用Fluent商业软件作为求解器进行稳态计算,工质选择理想气体。根据与试验结果的对比,不断地调整数值计算中选用的湍流模型、离散方法等,最终确定湍流模型选为SST k -ω模型,SIMPLEC算法,差分格式为二阶迎风。在高速计算中,为保证与低速计算的动力相似,保持高低速相同的出口雷诺数Re2=1.6 × 106,高速状态下的出口马赫数Ma2=0.65,低速状态下的出口速度约为V2=12 m/s,从而确定高低速的模化比为18.65,统一进口气流角为α=37.7°,进口湍流强度Tu∞=4%。图 3是T106A在低速实验和低速数值模拟下叶片表面的静压系数分布,横坐标为以前缘为起点的无量纲弧长,纵坐标为静压系数定义为Cp=(P01 -P)/(P01 -P2)。从中可以看出,数值模拟得到的数据与实验数据基本相符,可以认定使用的模型和求解器可信。
|
图 3 T106A压力系数分布 Fig. 3 T106A Cp distribution along the dimensionless curve length |
根据低速数值计算确定的湍流模型、进出边界条件以及离散方法等设置,计算T106A平面叶栅在高速状态下叶片表面的静压系数的分布如图 3所示。图 3可以看出在不同的高低速状态下,高速和低速的叶片表面静压系数的分布有很大不同,尤其是吸力面0%~60%弦长区域范围内。分析主要原因是高速和低速状态下,流体压缩性的不同导致了叶片表面压力系数以及流场中参数的分布不同。
2.2 叶型优化流程根据上述分析可知,如果将高速涡轮叶片直接模化放大,放在低速风洞中得到叶片上的压力系数与高速将会有很大的不同,所以必须将叶型进行修改再设计来弥补由于高低速气体压缩型不同导致的压力系数分布的不同。叶型优化再设计目标是让重新设计的叶型与T106A在高速下在叶片上有相同的压力系数分布。
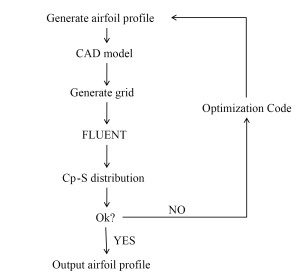
叶型优化设计流程如图 4所示,其中占据优化主要时间的部分为流场计算,故在整个优化再设计流程中采用二维平面叶栅模型,且在优化计算流程时采用粗网格进行计算减少优化时间,使用ICEM脚本文件实现网格的自动划分,与三维网格保持相同的平面拓扑结构,二维网格节点数约为30000,在叶片周围布置21层O型网格,栅距方向和轴向网格点数为100 × 254。整个过程无人为因素参与,最终得到的优化叶型如图 5所示,命名为LSA,对比分析T106A和LSA可知,LSA在叶片前缘部分与T106A几乎重合,LSA在叶片弦长中后部的厚度要大于T106A,两者厚度上的差异与高低速空气压缩性的不同相吻合。
|
图 4 优化过程 Fig. 4 Optimization process |
|
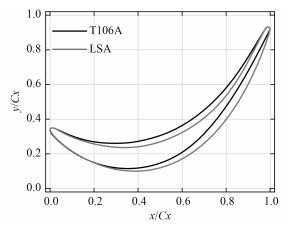
图 5 叶型模型对比 Fig. 5 The modified airfoil |
图 5为通过优化得到的低速叶型LSA和原始高速叶型T106A,LSA整体上明显要比原始叶型T106A厚,尤其是在靠近中后段尾缘的部位。根据优化最终得到的低速叶型LSA,对T106A和LSA分别在高速和低速下进行精细的三维稳态数值计算,保持与原始三维计算相同的湍流模型、离散方法以及边界条件。在三维数值模拟中,高速状态下T106A流场中最大马赫数Ma=0.95,流场中没有激波存在。
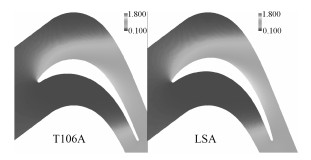
图 6为高低速叶栅三维数值计算结果中径位置处的压力系数云图,通过对比二者流场差距很小。图 7为叶片表面中径位置处的压力系数分布图,二者虽然在吸力面后半段出现了细微的差异,但是在最大压力系数出现的位置以及压力系数整体分布上几乎完全相同,可以认为在二维状态下进行有目标叶型优化是有效的,LSA是T106A在低速模化下有效的对应叶型。
|
图 6 中径位置的压力系数云图 Fig. 6 Cp distribution contour at middle span |

|
图 7 中径处的压力系数分布 Fig. 7 Cp distribution at middle span |
对应于中径位置处的流场以及叶片表面的压力系数分布,LSA和T106A出现了比较符合的对应关系,下文将给出流场中具体二次流中叶顶泄漏流的相关分析。定义当地的质量通量系数(mass flux rate)如下:
| $ mass\;flux\;rate = \frac{{mass\;flu{x_{local}} \cdot {A_{local}}}}{{inlet\;mass\;flow\;rate}}{\rm{.}} $ |
图 8为吸力面在叶顶区域延伸面上的质量通量系数分布云图,二者在泄漏量的分布上基本保持一致,但是在泄漏量的大小上有较大的差异。最大泄漏出现的位置出现了一定后移,低速叶栅LSA的泄漏量明显要大于高速T106A的泄漏量,但总体趋势基本保持一致。

|
图 8 叶顶位置的质量通量系数分布云图 Fig. 8 Mass flux rate distribution at tip region |
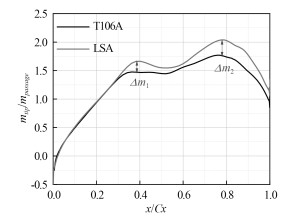
图 9为泄漏量在叶顶间隙区域沿轴向弦长的分布,由图 8在叶顶间隙区内沿叶高方向的积分所得。从图中可以很明显的看出,LSA的整体泄漏强度要大于T106A,尤其是在△m1和△m2两个位置,大约对应40%和80%的轴向弦长。对比于高速T106A,低速LSA出现最大泄漏的位置出现了一定的后移。对于叶顶间隙处确定的吼道面积,叶顶泄漏流主要是由压力梯度引起的,由于高速和低速在叶顶间隙位置处压力面和吸力面压力梯度的不同,最终导致泄漏量分布的不同。
|
图 9 质量通量沿轴向弦长分布 Fig. 9 Tip leakage flow mass flux ratio |
定义当地总压损失系数为:
| $ \xi = \left( {{P_{01}} - {P_0}} \right)/0.5\rho {v^2}。 $ |
式中:0.5ρv2为叶栅出口动压;P0为当地总压;P01为进口总压。
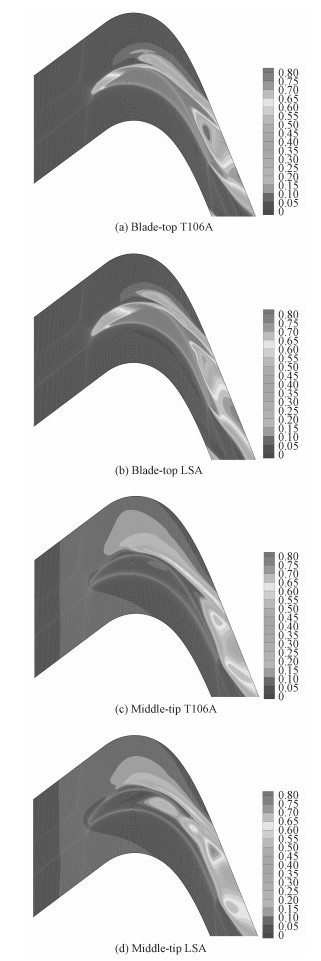
图 10为当地总压损失系数在叶顶间隙区域的分布,其中blade-top是叶片顶部截面,middle-tip是上端壁面和叶片顶部面的中间截面。通过对比T106A和LSA的在2个截面流场,二者在分布上基本保持一致,但是在叶片尾缘靠近吸力面的一侧出现了比较大的不同。在叶片顶部端面,低速LSA出现泄漏的起始位置要落后于T106A叶栅。根据middle-tip截面的当地总压损失系数可知,对比于高速T106A叶栅,低速LSA在叶顶区域压力面附近出现了一个高损失区,这与高速T106A有很大的不同。
|
图 10 叶顶区域当地总压损失系数的分布云图 Fig. 10 The total pressure loss coefficient distribution |
图 11为当地总压损失系数沿轴向通道的云图,分别给出了50%、100%以及110%弦长位置截面的总压损失系数云图。从50%弦长位置可以很明确的看出,在叶顶区域尤其是叶片上方区域,不论从强度还是范围上看高速T106A的损失都要远大于低速LSA。100%以及110%弦长位置的云图更加明确地证实了高速T106A泄漏涡的大小以及强度都要高于低速LSA。
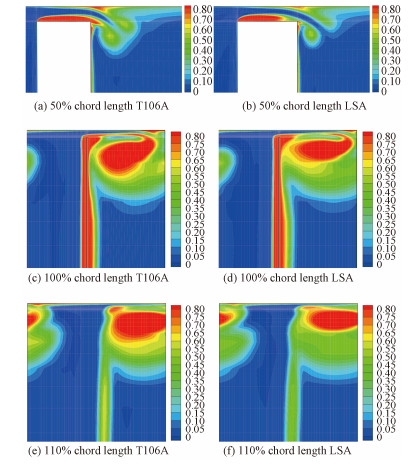
|
图 11 轴向位置沿流道的总压系数损失云图 Fig. 11 The total pressure loss coefficient distribution along the passage length |
定义沿叶片在叶顶间隙的延伸区域为叶顶区域(tip blade region),整个流道区域为passage。表 2给出了高速T106A和低速LSA流场相关统计量的对比,二者除了在叶顶区域的当地总压损失系数LSA比T106A大23%以外,其他统计量的差距不大。
|
|
表 2 T106A和LSA叶顶区域和流道相关统计量对比 Tab.2 The details of T106A and LSA at tip blade region and whole passage |
图 12给出了当地总压损失系数沿流道分布,横轴为无量纲的轴向距离,纵轴为总压损失系数,通过在不同流道位置截面上的总压损失系数积分达到。从图中可以看出,在叶片通道区域内,高速T106A叶栅的损失始终大于低速LSA,并且在叶栅出口处达到最大,出口处LSA的总压损失要比T106A小10%左右。

|
图 12 整个通道中不同位置的总压损失系数分布 Fig. 12 The total pressure loss efficient distribution along axial for whole passage |
本文采用贝塞尔曲线对涡轮叶片进行参数化,通过遗传优化算法对高速叶栅T106A进行再设计,获得的叶型LSA在低速风洞中与T106A高速叶栅在中径位置的叶片表面压力系数相同分布。同时对比T106A和LSA在三维数值计算中的泄漏流以及流道中损失分布,得到以下结论:
1) 对比带叶顶间隙的高低速叶栅,LSA比T106A的泄漏量约大12%;但T106A叶栅的泄漏涡大小和强度要明显高于低速叶栅LSA,流道的总压损失比T106A要小10%左右;
2) 即使通过修改叶型匹配中径处的压力系数的分布以后,在叶顶间隙处以及整体流道的损失分布上高低速仍然存在较大的差异。
3) 对于在叶顶间隙处的差异,提出以下可能的解决思路:在中径位置上匹配压力系数的分布,在叶顶间隙处进行特殊处理,设计不等距的叶顶间隙,思路如图 13所示。在叶顶间隙处不等距按照流线上的压力梯度来进行匹配,这样能够保证在中径处的压力系数的匹配,同样能够保证在叶顶间隙处质量流量分布的匹配。可能带来的问题是由于在叶片的叶顶进行不等距处理,会导致在其表面上出现流动分离等,流道中的损失会增加。

|
图 13 叶顶间隙处理方式 Fig. 13 The sketch up for variable distance tip clearance |
| [1] | HODSON, H. P, DOMINY, R. G., Annular Cascades. Advanced methods for cascade testing, 1993, AGARD-AG-328. |
| [2] | WISLER, D. C, Loss reduction in axial flow compressors through low-speed model testing. 1984, ASME paper 84-GT-184. |
| [3] | MICHELE, M., FILIPPO, R., ROBERTO, P. et al. Redesign of high-lift LP-turbine airfoils for low speed testing[C]//Proceedings of ASME Turbo Expo 2010:Power for Land, Sea and Air, GT2010, GT2010-23284 |
| [4] | ZHANG, X. F., VERA, M., HODSON, H., 2006, Separation and transition control on an aft-Loaded ultra-high-lift LP turbine blade at low reynolds numbers:low-speed investigation[J]. Journal of Turbomachinery, ASME, Vol. 128, pp. 517-527 |
| [5] | VERA, M., ZHANG, X. F., HODSON, H. Separation and transition control on an aft-loaded ultra-high-lift LP turbine blade at low reynolds numbers:high-speed validation[J]. Journal of Turbomachinery, ASME, 2007, Vol. 129, pp. 340-347 |
| [6] | BREAR, M. J., HODSON, H. P., GONZALEZ, P., et al. Pressure surface separations in low-pressure turbines-part 2:Interactions With the Secondary Flow[J]. Journal of Turbomachinery, ASME, 2002, Vol. 124, pp. 402-409 |
| [7] | GONZÁLEZ P., ULIZAR I., VÁZQUEZ R., et al, Pressure and suction surfaces redesign for high-lift low-pressure turbines[J]. Journal of Turbomachinery, 2002, ASME, Vol. 124, pp. 161-166 |
| [8] | MACIEJ M. O, RICHARD L. T, HOWARD P. H., Boundary layer transition on the high lift T106A low-pressure turbine blade with an oscillating downstream pressure field[J]. Journal of Turbomachinery, 2008, ASME, Vol. 130, pp. 021009-1-10 |
 2016, Vol. 38
2016, Vol. 38
