0 引言

螺旋桨引起的激振力通过轴系各轴承传递给船体，并引起振动与噪声，是影响船舶舒适性和安全性的主要因素之一。对船舶轴系各轴承位置在垂向和纵向进行优化布置，从而控制轴承处的传递力，将有利于从传递路径上实现船体尾部的减振降噪。

轴承的纵向位置发生变化，将会改变轴系结构参数，使弯曲振动发生改变。周春良等^[1]分析了不同轴承支撑长度及间距对船舶振动特性的影响；朱小平^[2]以螺旋桨在x向和y向的最大冲击响应和最大加速度响应作为优化目标，利用遗传算法对轴系支撑位置进行多目标优化。

与普通高速旋转机械不同，船舶轴系由于较大的自重和出于对轴承保护的原因必须进行轴系校中，改变轴承在轴向和垂向的位置，以使各轴承的载荷在合理的范围之内。轴系的校中优化从单一的以轴承径向变位值为变量，以尾轴后轴承受力最小为目标函数的单向单目标优化^[3-4]逐渐发展成为以轴承径向和轴向位移为变量，以多工况下尾轴后轴承最小受力、各轴承受载均匀等为目标函数的双向多目标优化^[5-8]。

轴承的位置布置不仅影响振动，还会影响校中效果。然而，之前的研究中，轴承位置对轴系振动影响并未计及对校中的影响；同样，对轴系校中的优化布置也忽略了对振动的影响。近年来，随着对乘坐舒适性和安全性的要求逐渐提高，船体尾部结构振动噪声的问题越发突出，与之前给出的目标函数不同的是，这里主要考虑由于螺旋桨轴承力的垂向分量所引起的船体尾部振动和噪声，所以本文以减小尾轴后轴承的受力响应为目的，在满足轴系校中要求的情况下，对船舶轴系轴承位置进行优化布置。

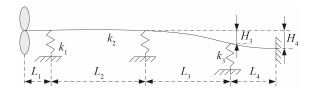
1 利用传递矩阵法求解轴系校中模型

轴系简化模型如图 1所示，从左至右依次为：螺旋桨、尾轴后轴承、尾轴中间轴承、尾轴前轴承以及推力轴承。力与位移向上为正方向，力矩使梁凹则为正、凸则为负，转角逆时针为正方向。

设空间状态向量为$S = {\left( {\begin{array}{*{20}{c}}H &\alpha &N&Q&1\end{array}} \right)^{\rm{T}}}$，H为轴承径向高度，α为截面转角，N为转矩，Q为剪力。设${S_0} = {\left( {\begin{array}{*{20}{c}} H&\alpha &N&Q&1 \end{array}} \right)_0}^{\rm{T}}$为轴系最末端的状态向量，${S_i} = {\left( {\begin{array}{*{20}{c}} H&\alpha &N&Q&1 \end{array}} \right)_i}^{\rm{T}}(i = 1, 2, 3, 4)$分别为各轴承支撑处左端的状态向量。一般设尾轴后轴承和尾轴中间轴承的高度为0，两者连线设为零轴线，当H₃和H₄为负时，说明轴承位置在零轴线之下，反之则在零轴线之上。

对螺旋桨左右两端状态向量建立方程有：

$ {\left( {\begin{array}{*{20}{c}} H\\ \alpha \\ N\\ Q\\ 1 \end{array}} \right)^L} = \left[ {\begin{array}{*{20}{c}} 1 &0&0&0&0\\ 0&1&0&0&0\\ 0&0&1&0&0\\ 0&0&0&1&{ - P}\\ 0&0&0&0&1 \end{array}} \right]{\left( {\begin{array}{*{20}{c}} H\\ \alpha \\ N\\ Q\\ 1 \end{array}} \right)^R}。 $

(1)

其中P为螺旋桨的附水总重量。其传递矩阵表达式为：

$ {B_0} = \left[ {\begin{array}{*{20}{c}} 1 &0&0&0&0\\ 0&1&0&0&0\\ 0&0&1&0&0\\ 0&0&0&1&{ - P}\\ 0&0&0&0&1 \end{array}} \right]。 $

(2)

同样对第i个轴段左右两端状态向量建立方程，可得其传递矩阵为B_i (i≥1)：

$ {B_i} = \left[ {\begin{array}{*{20}{c}} 1 &L&{\frac{{{L_i}^2}}{{2EI}}}&{\frac{{{L_i}^3}}{{6EI}}}&{ - \frac{{q{L_i}^4}}{{24EI}}}\\ 0&1&{\frac{{{L_i}}}{{EI}}}&{\frac{{{L_i}^2}}{{2EI}}}&{ - \frac{{q{L_i}^3}}{{6EI}}}\\ 0&0&1&L&{ - \frac{{q{L_i}^2}}{2}}\\ 0&0&0&1&{ - qL}\\ 0&0&0&0&1 \end{array}} \right],(i \ge 1)。 $

(3)

式中：$q = \rho Ag$为线密度，ρ材料密度，A为截面积，g为重力加速度，取10 m/s²；E为弹性模量；EI为截面惯性矩。

设${B_{ijkmn}} = {B_i}{B_j}{B_k}{B_m}{B_n}$，则：${B_{10}} = {B_1}{B_0}$，${B_{210}} \!= \!{B_2}{B_1}{B_0}$，${B_{3210}} \!=\! {B_3}{B_2}{B_1}{B_0}$，${B_{43210}} \!=\! {B_4}{B_3}{B_2}{B_1}{B_0}$，${B_{32}} = {B_3}{B_2}$，${B_{432}} = {B_4}{B_3}{B_2}$，${B_{43}} = {B_4}{B_3}$，故有：

$ {S_1} = {\left( {\begin{array}{*{20}{c}} H\\ \alpha \\ N\\ Q\\ 1 \end{array}} \right)_1} = {B_1}{B_0}{\left( {\begin{array}{*{20}{c}} H\\ \alpha \\ N\\ Q\\ 1 \end{array}} \right)_0} = {B_1}{B_0}{S_0} = {B_{10}}{S_0}。 $

(4)

则有方程：

$ {H_1} = {B_{10}}(1, 1){H_0} + {B_{10}}(1, 2){\alpha _0} + {B_{10}}(1, 5)。 $

(5)

即

$ {B_{10}}(1, 1){H_0} + {B_{10}}(1, 2){\alpha _0} = {H_1}-{B_{10}}(1, 5)。 $

(6)

同理：

$ \begin{array}{*{20}{l}} {{{\left( {\begin{array}{*{20}{c}} H\\ \alpha \\ N\\ Q\\ 1 \end{array}} \right)}_2} = {B_2}\left[{{{\left( {\begin{array}{*{20}{c}} H\\ \alpha \\ N\\ Q\\ 1 \end{array}} \right)}_1} + \left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ {{F_1}}\\ 0 \end{array}} \right)} \right] = {B_2}{B_{10}}{{\left( {\begin{array}{*{20}{c}} H\\ \alpha \\ N\\ Q\\ 1 \end{array}} \right)}_0} + }\\ {\quad \quad \quad \quad {B_2}\left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ {{F_1}}\\ 0 \end{array}} \right) = {B_{210}}{{\left( {\begin{array}{*{20}{c}} H\\ \alpha \\ N\\ Q\\ 1 \end{array}} \right)}_0} + {B_2}\left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ {{F_1}}\\ 0 \end{array}} \right)。} \end{array} $

(7)

其中${F_i}(i{\rm{ = 1}},{\rm{2}},{\rm{3}},{\rm{4}})$为各轴承处的支持力。故有方程：

$ {H_2} = {B_{210}}(1, 1){H_0} + {B_{210}}(1, 2){\alpha _0} + {B_{210}}(1, 5) + {B_2}(1, 4){F_1}。 $

(8)

即

$ {B_{210}}(1, 1){H_0} + {B_{210}}(1, 2){\alpha _0} + {B_2}(1, 4){F_1} = {H_2}-{B_{210}}(1, 5)。 $

(9)

以此类推，同理可得：

$ \begin{array}{*{20}{c}} {{B_{3210}}(1,1){H_0} + {B_{3210}}(1,2){\alpha _0} + {B_{32}}(1,4){F_1} + }\\ {{B_3}(1,4){F_2} = {H_3} - {B_{3210}}(1,5){\rm{。}}} \end{array} $

(10)

$ \begin{array}{*{20}{c}} {{B_{43210}}(1, 1){H_0} + {B_{43210}}(1, 2){\alpha _0} + {B_{432}}(1, 4){F_1} + }\\ {{B_{43}}(1, 4){F_2} + {B_4}(1, 4){F_3} = {H_4}-{B_{43210}}(1, 5)。} \end{array} $

(11)

$ \begin{array}{*{20}{c}} {{B_{43210}}(2,1){H_0} + {B_{43210}}(2,2){\alpha _0} + {B_{432}}(2,4){F_1} + }\\ {{B_{43}}(2,4){F_2} + {B_4}(2,4){F_3} = {\alpha _4} - {B_{43210}}(2,5)。} \end{array} $

(12)

联合上述6式（8）~式（12），可得下式：

$ \begin{array}{*{20}{c}} {\left[{\begin{array}{*{20}{c}} {{B_{10}}(1, 1)}&{{B_{10}}(1, 2)}&{}&{}&{}\\ {{B_{210}}(1, 1)}&{{B_{210}}(1, 2)}&{{B_2}(1, 4)}&{}&{}\\ {{B_{3210}}(1, 1)}&{{B_{3210}}(1, 2)}&{{B_{32}}(1, 4)}&{{B_3}(1, 4)}&{}\\ {{B_{43210}}(1, 1)}&{{B_{43210}}(1, 2)}&{{B_{432}}(1, 4)}&{{B_{43}}(1, 4)}&{{B_4}(1, 4)}\\ {{B_{43210}}(2, 1)}&{{B_{43210}}(2, 2)}&{{B_{432}}(2, 4)}&{{B_{43}}(2, 4)}&{{B_4}(2, 4)} \end{array}} \right], }\\ {\left( {\begin{array}{*{20}{c}} H\\ \alpha \\ {{F_1}}\\ {{F_2}}\\ {{F_3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{H_1} -{B_{10}}(1, 5)}\\ {{H_2} -{B_{210}}(1, 5)}\\ {{H_3} -{B_{3210}}(1, 5)}\\ {{H_4} - {B_{43210}}(1, 5)}\\ {{\alpha _4} - {B_{43210}}(2, 5)} \end{array}} \right)。} \end{array} $

(13)

推力轴承处因为设为固定端，故截面转角${\alpha _4}$为0。推力轴承处的支持力设为${F_4}$，有方程：

$ \begin{array}{*{20}{c}} {{B_{43210}}(4, 1){H_0} + {B_{43210}}(4, 2){\alpha _0} + {B_{432}}(4, 4){F_1} + }\\ {{B_{43}}(4, 4){F_2} + {B_4}(4, 4){F_3} + {B_{43210}}(4, 5) + {F_4} = 0。} \end{array} $

(14)

即得：

$ \begin{array}{*{20}{c}} {{F_4} =-\left( {{B_{43210}}(4, 1){H_0} + {B_{43210}}(4, 2){\alpha _0} + {B_{432}}(4, 4){F_1} + } \right.}\\ {\left. {{B_{43}}(4, 4){F_2} + {B_4}(4, 4){F_3} + {B_{43210}}(4, 5)} \right)} \end{array} $

(15)

同样，可以求得其他各位置的状态向量参数。

2 利用传递矩阵法求解轴系弯曲振动响应

设传递矩阵状态矢量为

$ Z = {[\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} Y &\theta &M&V \end{array}} \end{array}]^{\rm{T}}}, $

式中：Y为截面处横向振动的位移幅值；θ为截面处转角幅值；M为截面处的弯矩幅值；V为截面处的剪力幅值。

定常轴向力作用下的梁的横向振动方程^[9]为：

$ m\frac{{{\partial ^2}u}}{{\partial {t^2}}} + T\frac{{{\partial ^2}u}}{{\partial {x^2}}} + EI\frac{{{\partial ^4}u}}{{\partial {x^4}}} = 0。 $

(16)

式中：$m = \rho A$为线密度；u为横向振动位移；T为轴向推力。

利用分离变量法求解上式，设其方程的解为：

$ u(x, t) = U(x)(B\sin \omega t + C\cos \omega t), $

(17)

代入原方程中可得：

$ EI\frac{{{d^4}U(x)}}{{d{x^4}}} + T\frac{{{d^2}U(x)}}{{d{x^2}}}-m{\omega ^2}U(x) = 0, $

(18)

此方程为一个4阶常系数常微分方程，4个根分别为：

$ \begin{array}{*{20}{c}} {{\lambda _1} = \sqrt {\frac{{\sqrt {{T^2} + 4m{\omega ^2}EI}-T}}{{2EI}}}, {\mkern 1mu} }&{{\lambda _2} =-\sqrt {\frac{{\sqrt {{T^2} + 4m{\omega ^2}EI}-T}}{{2EI}}}, }\\ {{\lambda _3} = \sqrt {\frac{{\sqrt {{T^2} + 4m{\omega ^2}EI} + T}}{{2EI}}} i, }&{{\lambda _4} = - \sqrt {\frac{{\sqrt {{T^2} + 4m{\omega ^2}EI} + T}}{{2EI}}} i。} \end{array} $

令${\alpha _1} = \sqrt {\frac{{\sqrt {{T^2} + 4m{\omega ^2}EI} + T}}{{2EI}}} $, ${\alpha _2} = \sqrt {\frac{{\sqrt {{T^2} + 4m{\omega ^2}EI}-T}}{{2EI}}} $,

则有：

$ Y = U(x) = {c_1}{\rm{sin}}{\alpha _1}x + {c_2}{\rm{cos}}{\alpha _1}x + {c_3}\sinh {\alpha _2}x + {c_4}\cosh {\alpha _2}x。 $

(19)

又因为：$\theta = \displaystyle\frac{{dY}}{{dx}}$，$M = EI\displaystyle\frac{{{d^2}Y}}{{d{x^2}}}$，$V = \displaystyle\frac{{dM}}{{dx}}$，写成矩阵形式为：

$ \begin{array}{*{20}{c}} {\left[{\begin{array}{*{20}{c}} Y\\ \theta \\ M\\ V \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\sin {\alpha _1}x}\\ {{\alpha _1}\cos {\alpha _1}x}\\ {-EI{\alpha _1}^2\sin {\alpha _1}x}\\ {-EI{\alpha _1}^3\cos {\alpha _1}x} \end{array}} \right.\begin{array}{*{20}{c}} {\cos {\alpha _1}x}\\ {-{\alpha _1}\sin {\alpha _1}x}\\ { - EI{\alpha _1}^2\cos {\alpha _1}x}\\ {EI{\alpha _1}^3\sin {\alpha _1}x} \end{array}}\\ {\left. {\begin{array}{*{20}{c}} {\sinh {\alpha _2}x}\\ {{\alpha _2}\cosh {\alpha _2}x}\\ {EI{\alpha _2}^2\sinh {\alpha _2}x}\\ {EI{\alpha _2}^3\cosh {\alpha _2}x} \end{array}\begin{array}{*{20}{c}} {\cosh {\alpha _2}x}\\ {{\alpha _2}\sinh {\alpha _2}x}\\ {EI{\alpha _2}^2\cosh {\alpha _2}x}\\ {EI{\alpha _2}^3\sinh {\alpha _2}x} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{c_1}}\\ {{c_2}}\\ {{c_3}}\\ {{c_4}} \end{array}} \right]。} \end{array} $

(20)

令

$ \begin{array}{*{20}{c}} {B(x) = {\rm{ }}\left[{\begin{array}{*{20}{c}} {\sin {\alpha _1}x}\\ {{\alpha _1}\cos {\alpha _1}x}\\ {-EI{\alpha _1}^2\sin {\alpha _1}x}\\ {-EI{\alpha _1}^3\cos {\alpha _1}x} \end{array}} \right.\begin{array}{*{20}{c}} {\cos {\alpha _1}x}\\ {-{\alpha _1}\sin {\alpha _1}x}\\ { - EI{\alpha _1}^2\cos {\alpha _1}x}\\ {EI{\alpha _1}^3\sin {\alpha _1}x} \end{array}}\\ {\left. {\begin{array}{*{20}{c}} {\sinh {\alpha _2}x}\\ {{\alpha _2}\cosh {\alpha _2}x}\\ {EI{\alpha _2}^2\sinh {\alpha _2}x}\\ {EI{\alpha _2}^3\cosh {\alpha _2}x} \end{array}\begin{array}{*{20}{c}} {\cosh {\alpha _2}x}\\ {{\alpha _2}\sinh {\alpha _2}x}\\ {EI{\alpha _2}^2\cosh {\alpha _2}x}\\ {EI{\alpha _2}^3\sinh {\alpha _2}x} \end{array}} \right]。} \end{array} $

(21)

当x=0时有：$Z(0) = B(0) \cdot C$；当x=l时有：$Z(l) = B(l) \cdot C$。综合两式有：

$ Z(l) = B(l) \cdot C = B(l) \cdot {B^{-1}}(0) \cdot Z(0)3 $

(22)

此即为考虑轴向力后的梁段传递矩阵。

此外, 考虑陀螺效应的螺旋桨的传递矩阵为：

$ {\boldsymbol{P}_0} = \left[ {\begin{array}{*{20}{c}} 1 &0&0&0\\ 0&1&0&0\\ 0&{(jh - 1){J_{dw}}{\Omega ^2}}&1&0\\ {{m_{pw}}{\Omega ^2}}&0&0&1 \end{array}} \right]。 $

(23)

轴承用弹性元件模拟，其传递矩阵为：

$ {\boldsymbol{P}_i} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ { - {k_i}}&0&0&1 \end{array}} \right],{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (i = 1,2,3)。 $

(24)

式中：Ω为轴系回旋振动角频率；ω为推进轴系的旋转角速度；m为螺旋桨在空气中的质量；${B_m}$为螺旋桨的附水系数；${m_{pw}}$$为添加附水系数后的螺旋桨质量；${J_p}$为螺旋桨在空气中的极转动惯量；${B_p}$为螺旋桨极转动惯量的附水系数；${J_{pw}}$为添加附水系数后的螺旋桨极转动惯量；${J_d}$为螺旋桨在空气中的径向转动惯量；${B_d}$为螺旋桨径向转动惯量的附水系数；${J_{dw}}$为添加附水系数后的螺旋桨径向转动惯量；$j = {J_{pw}}/{J_{dw}}$；$h = \omega /\Omega $；${k_i}$为对应轴承的支撑刚度。

在尾轴末端垂向施加一单位幅值的简谐力后，利用传递矩阵法求解轴系各支撑位置处受力的响应幅值。整体的传递矩阵即为各元件矩阵相乘，设整体传递矩阵为T，有

$ \begin{array}{*{20}{c}} {\boldsymbol{T} = {\rm{ }}{P_0} \cdot Z({L_1}) \cdot {P_1} \cdot Z({L_2}) \cdot {P_2} \cdot Z({L_3}) \cdot {P_3} \cdot Z({L_4}) = }\\ {\left[{\begin{array}{*{20}{c}} {{T_{11}}}&{{T_{12}}}&{{T_{13}}}&{{T_{14}}}\\ {{T_{21}}}&{{T_{22}}}&{{T_{23}}}&{{T_{24}}}\\ {{T_{31}}}&{{T_{32}}}&{{T_{33}}}&{{T_{34}}}\\ {{T_{41}}}&{{T_{42}}}&{{T_{43}}}&{{T_{44}}} \end{array}} \right]。} \end{array} $

(25)

$ {\left[{\begin{array}{*{20}{c}} Y\\ \theta \\ M\\ V \end{array}} \right]_{{\rm{始端}}}} = \left[{\begin{array}{*{20}{c}} {{T_{11}}{T_{12}}{T_{13}}{T_{14}}}\\ {{T_{21}}{T_{22}}{T_{23}}{T_{24}}}\\ {{T_{31}}{T_{32}}{T_{33}}{T_{34}}}\\ {{T_{41}}{T_{42}}{T_{43}}{T_{44}}} \end{array}} \right]{\left[{\begin{array}{*{20}{c}} {{Y_0}}\\ {{\theta _0}}\\ {{M_0}}\\ {{V_0}-F} \end{array}} \right]_{末端}}。 $

(26)

把螺旋桨端视为自由端，将推力轴承端视为固定端，上式变为：

$ {\left[{\begin{array}{*{20}{c}} 0\\ 0\\ M\\ V \end{array}} \right]_{{\rm{始端}}}} = \left[{\begin{array}{*{20}{c}} {{T_{11}}{T_{12}}{T_{13}}{T_{14}}}\\ {{T_{21}}{T_{22}}{T_{23}}{T_{24}}}\\ {{T_{31}}{T_{32}}{T_{33}}{T_{34}}}\\ {{T_{41}}{T_{42}}{T_{43}}{T_{44}}} \end{array}} \right]{\left[{\begin{array}{*{20}{c}} {{Y_0}}\\ {{\theta _0}}\\ 0\\ {0-F} \end{array}} \right]_{{\rm{末端}}}}。 $

(27)

可解得：

$ {Y_0} = \frac{{{T_{14}} \cdot {T_{22}}-{T_{12}} \cdot {T_{24}}}}{{{T_{11}} \cdot {T_{22}}-{T_{12}} \cdot {T_{21}}}} \cdot F, \;{\theta _0} = \frac{{{T_{11}} \cdot {T_{24}}-{T_{14}} \cdot {T_{21}}}}{{{T_{11}} \cdot {T_{22}} - {T_{12}} \cdot {T_{21}}}} \cdot F。 $

(28)

得到初始向量后，可利用传递矩阵求得包括尾轴后轴承在内的任一轴承处的位移幅值，并得到轴承力的响应幅值。

3 利用拟定常法求解螺旋桨处轴承力叶频和倍叶频的幅值比值

螺旋桨桨叶在不均匀的伴流场中运转时会受到脉动力的作用，并通过轴承传递给船体，其称为轴承力，频率成分为叶频和倍叶频^[10]。所以螺旋桨轴承力为多个频率成分的叠加，船舶轴系结构设计过程中不应只对单一频率进行减振控制。对于船舶螺旋桨轴承力, 一般较大的频率幅值集中在低倍数次叶频，这里研究叶频和2倍叶频的轴承力垂向分量的幅值比值，并将其当作权系数用来求解叶频和2倍叶频轴承力共同作用下的尾轴后轴承的受力响应。

螺旋桨轴承力的研究方法中，拟定常方法作为一种经验方法，使用简便，可满足工程需要, 此处利用拟常定法进行分析。拟定常法假定某位置螺旋桨非定常运动特性由该位置定常流的特性来代替，此方法将当地的进速系数$J(\varphi )$值确定的推力系数${K_T}(\varphi )$和${K_Q}(\varphi )$定义为螺旋桨此时的特性，并认为推力和转矩集中于桨叶的某一半径位置，称为代表半径（通常为0.7倍的半径处），$J(\varphi )$由此位置处求出^[10]。

根据文献[10]可知，在忽略切向伴流的情况下，垂向力的各阶幅值为：

$ \begin{array}{*{20}{c}} {{{({F_z})}_k} = {\rm{ }}\frac{{{Q_0}}}{{2r}} \cdot \frac{{{{K'}_{Q0}}}}{{{K_{Q0}}}} \cdot \frac{{{J_0}}}{{1-{w_0}}} \times }\\ {\sqrt {{{({w_{kZ-1, c}}-{w_{kZ + 1, c}})}^2} + {{({w_{kZ - 1, s}} - {w_{kZ + 1, s}})}^2}} 。} \end{array} $

(29)

式中：Z为叶数；r为半径；${w_0}$，${w_{kZ - 1, c}}$，${w_{kZ + 1, c}}$，${w_{kZ - 1, s}}$，${w_{kZ + 1, s}}$为该半径上的调谐成分，并有$w = {w_0} + \displaystyle\sum\limits_{n = 1}^\infty {({w_{n, c}} \cdot \cos n\varphi + {w_{n, s}}\sin n\varphi )} $。

$ {J_0} = \frac{V}{{nD}}(1-{w_0}) $

式中：V为船速；D为螺旋桨直径；n为转速；${K_{T0}}$和${K_{Q0}}$为此时$J = {J_0}$对应的推力和转矩系数，并有${Q_0} \!=\! {K_{Q0}} \cdot \rho {n^2}{D^5}$，${K'_{Q0}} \!=\! - {(\displaystyle\frac{{d{K_Q}}}{{dJ}})_{J \!=\! {J_0}}}$。

这样第i阶叶频和第j阶的轴承力中的垂向分量幅值之比为：

$ \frac{{{{({F_z})}_i}}}{{{{({F_z})}_j}}} = \frac{{\sqrt {{{({w_{iZ-1, c}}-{w_{iZ + 1, c}})}^2} + {{({w_{iZ-1, s}} - {w_{iZ + 1, s}})}^2}} }}{{\sqrt {{{({w_{jZ - 1, c}} - {w_{jZ + 1, c}})}^2} + {{({w_{jZ - 1, s}} - {w_{jZ + 1, s}})}^2}} }}。 $

(30)

由上式可发现，当知道此时的伴流调谐成分时，不同阶数的幅值之比即可确定。

参照文献[11]中的伴流场进行理论分析，按其提供的5叶大侧斜螺旋桨Semiun-Maru HSP桨桨盘处0.7倍半径处轴向分量的伴流分布傅氏系数可知：${\left( {{F_z}} \right)_1}/{\left( {{F_z}} \right)_2} = 5.734$，即${\left( {{F_z}} \right)_2} = 0.1744{\left( {{F_z}} \right)_1}$，0.174 4即为权系数。

4 利用Isight对轴系实例模型进行优化设计

Isight是一款基于参数的多学科设计优化软件，不仅提供了多种优化算法可供选择，还与Matlab等众多软件设有接口，使其应用广泛。将求解轴系校中和弯曲振动响应的Matlab程序导入Isight中，并有如下设置：

1） 自变量设置：以尾轴后轴承及尾轴中间轴承两者连线所在的直线为水平线，尾轴前轴承和推力轴承的高度设置为H₃和H₄；船舶轴系轴承纵向布置方面，尾轴后轴承、尾轴中间轴承以及推力轴承位置不变，只改变尾轴前轴承位置。

2） 目标函数设置：在轴系末端给予一垂向单位谐波激振力，分别计算出尾轴后轴承受力响应F_z1和尾轴中间轴承受力响应F_z2，目标函数为

$ {F_Z} = {F_z}_1 + 0.174{\mkern 1mu} 4{F_z}_2。 $

(31)

其中0.174 4为之前求出的权系数。

参考中华人民共和国船舶行业标准CB/Z 338— 2005以及各大船级社的要求，设置如下约束条件：

1） 尾轴各轴承许用比压为0.3 MPa，推力轴承为0.6 MPa，最大载荷的计算公式为：

$ {F_{\max }} = [P] \cdot L \cdot d $

(32)

式中：[P]为许用比压；L为轴承衬的长度；d为位于轴承内部轴段的轴颈外径。

计算可得轴系校中过程中，艉轴后、中、前轴承及推力轴承的的最大载荷分别为135 kN，100 kN，120 kN以及120 kN。

2） 轴承负荷应不小于相邻两跨距间所有重量总和的20%；

3） 尾轴后轴承支撑点处截面转角小于3.5 × 10^-4rad；

4） 尾轴前、中、后各轴承处弯曲应力均小于20 MPa，推力轴承处弯曲应力小于15 MPa。

优化方法：Pointer优化器是Isight提供的智能自动优化专家，将线性单纯形法、序列二次规划法、最速下降法及遗传算法等4种算法进行组合，从而形成一个最优的优化策略^[12]。这里选用Pointer优化器对轴系系统进行优化。

轴系具体参数如表 1所示。优化结果如表 2所示。

可见在满足轴系校中的情况下，经过优化之后，艉轴后轴承的响应在原有的基础上减小了8.13%，证明了方法的有效性。

5 结语

船舶轴系由于较大的自重，出于对轴承保护的原因必须进行轴系校中，改变轴承在轴向和垂向的位置，以使各轴承的载荷在合理的范围之内。但轴承位置的改变同样会影响轴系的振动特性，从而改变传递特性。本文利用传递矩阵法分别建立了船舶轴系校中数学模型和弯曲振动数学模型，利用拟定常法得到螺旋桨叶频和二次倍叶频的激励力幅值比值，成比例输入到轴系系统当中，以尾轴后轴承所受的垂向激励力最小为目标函数，对轴系轴承的纵向和垂向位置进行了优化布置，得到了满足轴系校中要求的最优解，实例中比原始布置方案减小了8.13%，证明了该方法的有效性，为船舶轴系布置提供了指导。