随着时代背景的演变,船舶朝着大型化、高功率化的方向发展,船舶柴油机的刚性也在不断加大[1-2],但是船体的刚性却相对变小,所以波浪对船舶柴油机的振动状态有着不可忽视的影响,各个隔振器的位置也因为船体变形而改变,造成船舶柴油机的振动情况发生改变,危害到船舶航行的安全,所以研究波浪载荷对柴油机振动影响具有非常重要的意义。
本文研究主要基于1艘集装箱船。利用Ansys有限元分析软件[3-4],首先对整个船舶进行网格划分,然后利用AQWA计算波浪的动压力,采用APDL语言编写加载程序实行波浪载荷的自动施加,利用惯性释放处理边界条件计算得出柴油机振动情况的变化。研究结果显示,波浪载荷对柴油机的振动状态比较恶劣的影响主要集中在低阶和高阶激励频率,避免低阶激励频率振动和高阶激励频率简谐应力作用的影响会对柴油机安全运行起到极大的帮助。
1 计算数学模型 1.1 波浪载荷的计算方程关于波浪载荷的计算有以下3个前提:
1) 将流体看作理想状况,即忽略粘性和压缩性;
2) 将流体质点运动作为没有旋转的势流运动处理;
3) 设定在微幅波的情况下,即波高相对波长非常小。
波浪运动和计算参数模型如图 1所示。

|
图 1 波浪运动图 Fig. 1 Wave motion graph |
波流场中的压力表达式如下:
| $ \Delta P =-\rho \frac{{\partial \varphi }}{{\partial t}}-\frac{1}{2}\rho \left( {{u^2} + {\nu ^2} + {\omega ^2}} \right)-\rho g\xi 。 $ | (1) |
式中:
选取一个随船运动的坐标系,设定X轴正向为船首方向,Y轴正向为船左侧,Z轴朝上。原点设定在船尾与船底中线相交处的竖线面、中剖面、纵剖面的交点。波浪的方向和X轴的夹角为β,规定船舶迎浪时,β=180°。设定在任何时刻,该坐标系都处于船舶摇晃的瞬时平衡位置,在傅汝德-克雷洛夫假设的条件下,得到波动压力的表达式为:
| $ \Delta P = \rho ga{e^{\kappa z}}\cos \left( {\kappa x{\rm{cos}}\chi-ky{\rm{sin}}\chi-{\omega _e}t} \right)。 $ | (2) |
波浪动压力在船体湿表面的积分,表示为在船体上作用的波浪扰动力和力矩:
| $ {F_W} =-\int \int s \Delta Pn{\rm{d}}S, $ | (3) |
| $ {{M}_{W}}=-\iint_{s}{\Delta P\left( r\times n \right)}\text{d}S。 $ | (4) |
式中:s为船体的湿表面积;n为s的单位外法线矢量,方向指向船体外部;r为动压力作用点相对于随船坐标系的位置向量。
按照船舶和柴油机力传递的比例关系,将以上分析的力加载到柴油机的底部,对柴油机进行谐响应分析,求出柴油机在波浪载荷下的振动规律。
1.2 柴油机谐响应方程通常意义上的谐响应分析是指在某一指定的频率范围内,结构受到循环载荷作用而产生相应的随频率变化的结构响应,并且做出响应—频率线型图。整体结构的动力平衡方程:
| $ [\boldsymbol{M}]\{ \boldsymbol{\mathop u}\limits^{..} \} + [\boldsymbol{C}]\{ \boldsymbol{\mathop u}\limits^. \} + [\boldsymbol{K}]\{ \boldsymbol{u}\} = \{ \boldsymbol{F}\}。 $ | (5) |
式中:[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;{F(t)}为结构外载荷矢量;
本文研究主要是基于1艘8530TEU集装箱船,其主要结构参数为:垂线间长320.00 m,型宽42.80 m,型深24.80 m,设计吃水14.65 m,排水量137 253 t。柴油机釆用单层6个隔振器支撑,参数如下:
气缸直径:0.17 m;
活塞行程:0.19 m;
额定功率:1 500 kW
发动机定转速:1 800 r/min;
最低稳定转速:600 r/min;
外形尺寸:长3.053 m;宽1.992 m;高1.770 m。
2.2 分析对象模型的绘制根据以上参数对计算物理模型进行绘制,应用Ansys有限元分析软件建立8530TEU集装箱船的有限元模型,主要采用SHELL163单元和BEAM188单元模拟船体板梁结构,模型包括95 728个单元和918 481个节点,模型如图 2所示。

|
图 2 船舶有限元模型 Fig. 2 Finite element model of ship |
根据柴油机的结构尺寸,运用PRO/E对柴油机进行模型的绘制,模型如图 3所示。

|
图 3 船舶发动机模型 Fig. 3 Ship engine model |
船舶柴油机受波浪载荷影响的时候,一般选择波浪弯矩最大的状态来进行研究[5-7],在波长和船长相等的情况下,波浪弯矩达到最大,来保证船舶航行的安全,因此,取波长
全球各大海域频繁出现的海情为2~6级浪,6级以上的波浪发生频率较低[8]。取较为常见的波高2 m,4 m和极限海况下波高H=6 m作为波浪波高,最终需要的波浪参数如表 1所示,
|
|
表 1 波浪参数表 Tab.1 Wave parameter list |
波浪来流方向为船首,入射角设为-180°,根据以上参数即可计算波浪载荷对柴油机振动的影响。
2.4 波浪载荷对柴油机振幅的影响在2 m,4 m和6 m波高时,柴油机受到波浪载荷的作用产生振幅,如图 4~图 6所示。
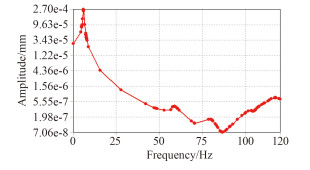
|
图 4 2 m波高的柴油机振幅 Fig. 4 Diesel engine amplitude of 2 m high wave |

|
图 5 4 m波高的柴油机振幅 Fig. 5 Diesel engine amplitude of 4 m high wave |
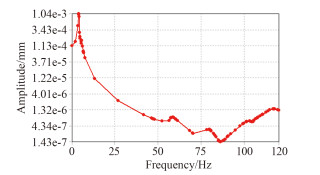
|
图 6 6 m波高的柴油机振幅 Fig. 6 Diesel engine amplitude of 6 m high wave |
由图可知,波浪载荷对柴油机的低阶振动影响比较明显,共振振幅较大,高阶响应振幅降低,振动的过度区域较陡;随着激励频率的升高,谐响应振动迅速降低;激励频率在50~100 Hz区间时,共振也会发生,但是振幅不是很大,和低阶共振的振幅相差3个等量级;在100~120 Hz的激励频率区间内,柴油机的振幅逐渐上升,但是上升的幅度不是很大。因此尽量避免低阶频率的对柴油机的激励作用,降低柴油机的谐响应振幅。
2.5 波浪载荷对柴油机受力的影响谐响应的应力作用会对柴油机产生疲劳破坏作用,因此柴油机受到波浪载荷的应力作用不可忽视,不同波高情况下柴油机受到的应力作用如图 7~图 9所示。

|
图 7 2 m波高的柴油机应力 Fig. 7 Diesel engine stress of 2 m high wave |
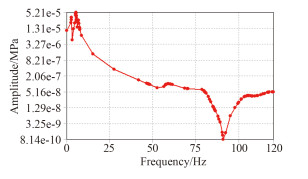
|
图 8 4 m波高的柴油机应力 Fig. 8 Diesel engine stress of 4 m high wave |
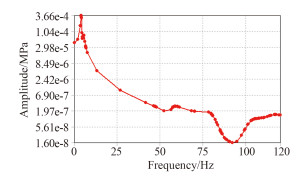
|
图 9 6 m波高的柴油机应力 Fig. 9 Diesel engine stress of 6 m high wave |
由图可知,波浪载荷对柴油机的低阶振动的应力影响比较大,共振应力较大,高阶响应下的应力降低,振动应力的过度区域较陡;随着激励频率的升高,谐响应振动应力迅速降低,低阶振动的应力相差3个等量级;如图所示在90 Hz附近时,会有无应力的情况发生,这样就会对柴油机产生很大的疲劳破坏作用,因此应该加装合适的隔振器,避免高阶和低阶频率对柴油机的激励作用。
综合以上分析,振动应力的激励频率和振幅的频率相对应,都有极大值和极小值,谐响应数值相差较大,谐响应作用比较明显,对柴油机有相当大的疲劳破坏作用
如果激励频率过小,柴油机的振幅和应力都较大,发生共振作用,柴油机动力特性就会减弱,导致柴油机运行不稳定;如果激励频率过大,柴油机的振幅和应力都会减到极低值,这样容易导致简谐力的作用,柴油机会发生疲劳破坏。因此对于同一柴油机,激励频率要适当,安装适当的隔振器对柴油机能够起到保护作用,及时对隔振器检查和检测,避免柴油机运行不稳定。
3 结语经过上述分析可得出以下结论:
1) 激励频率过小,柴油机的振幅和应力都较大,发生共振作用,柴油机动力特性就会减弱,导致柴油机运行不稳定;如果激励频率过大,柴油机的振幅和应力都会减到极小值,在此附近的激励会对柴油机造成疲劳破坏作用。
2) 对于同一柴油机,安装适当的隔振器对柴油机能够起到保护作用,波浪载荷对柴油机和隔振器有疲劳破坏作用,因此及时对隔振器检查和检测,避免柴油机运行不稳定。
3) 该研究分析对在海上航行的船舶安全提供了很大的帮助,为船舶柴油机的建造提供了理论技术支持,结论具有普遍使用性。
| [1] | 董恒建. 对轴系校中影响的船体变形研究[J]. 船舶工程 , 2009, 31 (增刊) :8–11. |
| [2] | 石磊. 用于轴系校中的船体变形计算研究[J]. 船舶工程 , 2010, 32 (3) :13–16. |
| [3] | 朱昀炤, 汪顺亭, 缪玲娟, 等. 船体变形对航姿参数的影响及其测量[J]. 微计算机信息 , 2008, 24 (22) :285–286, 57. |
| [4] | 朱昀炤, 汪顺亭, 缪玲娟, 等. 船体变形测量技术综述[J]. 船舶工程 , 2007, 29 (6) :58–61. |
| [5] | 吴谈.大型集装箱船推进轴系支承点处的变形与应力分析[D].武汉:武汉理工大学, 2013. |
| [6] | 唐卫军.大型集装箱船三维波浪载荷计算[D].武汉:武汉理工大学, 2006. |
| [7] | 何丽丝.超大型船舶在波浪中的动力响应分析[D].武汉:武汉理工大学, 2013. |
| [8] | 王锐利, 林大志. 船舶运动干扰载荷数学模型及计算方法研究[J]. 舰船科学技术 , 2016, 38 (4) :13–15. |
 2016, Vol. 38
2016, Vol. 38
