在大幅波浪中运动的船舶,由于受到波浪的强烈作用,会出现剧烈的摇荡,同时船舶与波浪间必然会出现猛烈的砰击现象。依据波浪与船体的作用位置划分,船舶受到的砰击类型主要有底部、外飘砰击及甲板上浪3种。随着船舶朝着大型化、高速化发展,其工作环境越来越恶劣,与此同时,各种极端海况所带来的首部外飘砰击、底部砰击、甲板上浪砰击也愈来愈严重。船体砰击往往会带来严重的后果,首先由于砰击瞬时波浪作用压力大,如果超过船体结构强度允许范围,会使砰击部位结构损坏;同时,砰击会使整个船体的振动加剧,当振动弯矩与波浪弯矩耦合叠加时,有可能会使船体受到的总纵弯矩过大从而导致总纵强度丧失。因此,在进行船体结构设计时,为满足规范对局部强度和总体强度的要求,都必须把船舶遭受的砰击载荷考虑进去[1]。
由于砰击是波浪与运动船体之间的非常剧烈的互相作用,它们互相影响,因此砰击具有明显的非线性特征。为此,有些学者根据不同的理论和方法,采用不同的简化措施,给出了各种计算非线性船舶摇荡运动以及波浪中载荷的可靠方法,其中“两步走”的方法得到了广泛应用,即先按刚体假设确定船舶运动,然后在已知运动响应的基础上再来计算相应海况下的砰击载荷[2]。由此可知,为了使计算的船舶波浪载荷更具合理性和可靠性,能够反映砰击作用的真实水平,必须对船舶的摇荡运动进行准确的计算。
综上所述,为了使设计的船舶满足安全性、舒适性以及快速性等航行性能的要求,必须在设计初期准确预报船舶在波浪中的运动响应,这是评价船舶耐波性的基础,也是后续计算船舶受到的砰击、上浪等载荷并进行合理船体结构设计的前提。
一直以来,许多学者对波浪中船体摇荡运动的研究作出了不懈的努力,取得了长足的进步,主要体现在研究方法上的转变:从二维理论到三维理论的转变、从线性方法到非线性方法的转变、从频域方法到时域方法的转变。切片理论是Karvin-kroukovsky在20世纪60年代首先提出的一种线性频域预报方法,该方法随后被广泛应用并被加以完善和改进,产生了许多新的方法,如新切片法、STF切片法、合理切片法等方法[3]。该方法虽然能得到符合工程应用要求的结果,却忽略了对一些重要的非线性因素的考虑,存在较多的假定和简化,在揭示船体运动力学机理和反应现实的准确性方面有很大不足,难以准确预报高航速下恶劣海况中的船体运动响应[4]。
根据大量的船模试验以及实船测量结果,可以看出,大幅波浪中的船体摇荡运动和船舶受到的波浪载荷的非线性特征突出,这是船体的非直壁结构形式以及剧烈波浪砰击等因素影响的结果[5]。三维水动力分析方法由于更接近实际情况而越来越受到人们的重视,主要包括自由面格林函数法和Rankine源法。自由面格林函数法是一种在船体表面分布点源和点汇来拟合船体周围流场,从而给出流场速度分布的势流方法[6]。该方法能够有效地解决零航速船舶在波浪中的运动问题,然而对于有航速的问题,该方法处理得到的结果并不十分准确,因为此时部分积分项的计算十分复杂[7]。Rankine面元法通过在物面以及自由面上都分布奇点来计算流场的速度势,该方法与自由面Green函数法相比,能够克服其计算复杂等缺点,而且对于影响矩阵的确定也相对较简便,有利于考虑非线性因素从而计算非线性摇荡运动[8]。
本文采用基于Rankine源方法的三维非线性时域势流理论,运用DNV/WASIM软件对标模DTMB5512进行耐波性预报,并将标模在水池中的耐波性试验结果以及采用线性切片方法预报的结果与上述计算结果进行对比分析。分析说明,对于有航速船舶的剧烈摇荡运动,该方法由于计及了流场压力计算式中的速度二次项、瞬时湿表面变化等非线性影响因素,能够对其进行更为合理精确的数值预报[9]。
1 船舶运动的势流理论在理想流体动力学中,通常对于不可压缩的、不考虑粘性的和认为涡量为零的流体,可以用一个速度势函数来描述流场中速度的分布情况[10]。当研究船舶与波浪之间互相作用的水动力学的问题时,上述速度势函数不仅要满足Laplace方程,还必须满足一定的初始条件以及相应的各种边界条件,这样才能够使方程有特定的解[10]。
1.1 基本假设大幅波浪中船体的摇荡运动以及船体波浪载荷的数值计算一般都离不开以下假设,通常包括:在静水中,可以认为船舶处于静稳定的平衡状态,也就是认为船体受到的重力与其排开水而受到的浮力相等;静水中航行时,船舶受到的静水阻力被认为等于推进器给它的推动力,同时,不考虑推进器对船体尾部流场的干扰,即认为流场只受到裸船体的扰动;将船舶的操纵运动和摇荡响应分开考虑,即认为它们相互间没有影响,计算运动响应时只考虑船体匀速直航状态[11]。根据以上假定,对波浪中船体运动响应进行受力分析,影响船体运动的外力主要有3个方面:1)波浪扰动力,包括入射波浪的变动水压力形成的流体动力即F-K力(傅汝德-克雷洛夫力)及波浪遇到船体产生绕射的绕射流体动力;2)船体摇荡运动(船动水不动)而产生的辐射流体动力;3)船体自身的质量力以及水的浮力[11]。
1.2 速度势对于大部分势流求解方法,一般都使用一个满足自由面边界条件的Green函数求解流场速度势,该程序使用一个简单的Rankine源作为Green函数来计算流场速度分布。由于这个Rankine源不自动满足任何边界条件,因而需要确定更多的方程来联立求解速度场。流场速度势
| $ \varphi (\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x}, t)-(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \xi }, t)G(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x}-\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \xi } )d\xi = \sigma (t)R(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} ){\rm{。}} $ | (1) |
动力边界条件:
运动边界条件:
初始时刻条件:
式中:z为水深;σ(t)为线性波动源的强度;ν为源的移动速度;
在求解过程中,如果只使用一个整体速度势φ很难获得稳定解。因此要将整体速度势φ分解为几个部分,每一部分只考虑有限的影响因素[13],即
| $ \varphi = {\varphi _B} + {\varphi _I} + {\varphi _M} + {\varphi _L}。 $ | (2) |
式中:φB为基本流动,考虑船体对流场的影响;φI为入射波势,考虑入射波的扰动;φM为记忆流,考虑船体对波浪的辐射作用;φL为局部流,用来满足船体的实际边界条件。
在自由面上:φL=0;
在船体表面上:
为了与实际情况一致,在波浪快达到网格边界的时候,要让其衰减从而阻止其继续传播。数值海岸是网格边界处的波浪吸收层[13]。在这个区域,运动自由表面条件为:
| $ \frac{{\partial \eta }}{{\partial t}} + v\frac{{\partial \eta }}{{\partial x}} = \frac{{\partial \varphi }}{{\partial z}}-2v\eta + \frac{{{v^2}}}{g}\varphi {\rm{。}} $ | (3) |
式中:
波浪中浮体的运动,可以用一个方程式来描述,即为:
| $ (\boldsymbol{M_{ij}} + {a_{ij}}){{\ddot x}_j}(t) + {b_{ij}}{{\dot x}_j}(t) + \int\limits_0^t {{K_{ij}}(t-\tau )} {{\dot x}_j}(\tau ){\rm{d}}\tau + (\boldsymbol{C_{ij}} + {c_{ij}}){x_j}(t) = {F_{iw}}(t)。 $ | (4) |
式中:Mij为广义质量矩阵;Cij为静水恢复力的矩阵。
| $ \boldsymbol{M_{ij}}{\rm{ = }}\left[{\begin{array}{*{20}{c}} m&0&0&0&0&0\\ 0&m&0&0&0&0\\ 0&0&m&0&0&0\\ 0&0&0&{{I_{11}}}&{{I_{12}}}&{{I_{13}}}\\ 0&0&0&{{I_{21}}}&{{I_{22}}}&{{I_{23}}}\\ 0&0&0&{{I_{31}}}&{{I_{32}}}&{{I_{33}}} \end{array}} \right]。 $ |
其中:m为船体的质量;Iij(i, j=1, 2, 3)为船体的惯性矩。
| $ \boldsymbol{C_{ij}}{\rm{ = }}\left[{\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&{{F_1}}&0&{{F_2}}&0\\ 0&0&0&{{F_3}}&0&0\\ 0&0&{{F_4}}&0&{{F_5}}&0\\ 0&0&0&0&0&0 \end{array}} \right]。 $ |
| $ {F_1} = \rho g{A_W}, {F_5} = \rho g\left( {{A_{\rm{W}}}d_1^2 + {z_B}\nabla } \right), $ |
| $ {F_3} = \rho g\left( {{A_{\rm{W}}}d_3^2 + {z_B}\nabla } \right), {F_5} = \rho g\left( {{A_{\rm{W}}}d_1^2 + {z_B}\nabla } \right), $ |
式中:m为船体质量;Iij(i, j=1,2,3)为船体的惯性矩;AW为水线面的面积;d1和d3为水线面绕铅垂方向(oz轴)和沿船长纵向方向(ox轴)的惯性半径;zB为浮心在垂向上的高度;xf为水线面漂心的纵坐标;▽为船体总的排水体积。
2 运动响应数值计算使用基于三维非线性时域势流理论的软件WASIM对标模DTMB5512进行不同航速下的运动响应数值预报,并与模型试验结果以及基于线性切片方法的计算结果进行对比分析,验证该软件能够更合理有效地预报船舶在波浪中的非线性运动响应。计算时主要选择2个航速,工况如表 1所示。
|
|
表 1 计算工况 Tab.1 Calculated conditions |
计算模型采用ⅡHR大学船模水池提供的标模DTMB5512,该模型具有方形尾封板和用作声呐导流罩的球首,如图 1所示。DTMB5512有已经公开的试验数据以及SMP的数值计算结果[14]。模型主尺度如表 2所示。

|
图 1 计算模型三维图 Fig. 1 3D model for calculation |
|
|
表 2 模型主尺度 Tab.2 Principles of scale model |
由于计算时间步长与网格沿船长方向大小有关,网格越小,达到收敛结果所需的时间步长越小。要保证网格能准确的适应船体曲面即尽可能的小,也要保证计算时间合理即不至于太长。因此网格采用分块加密的方式划分,在船体首尾曲面复杂的区域使用较细密的网格,在平行中体段使用较粗大的网格。划分后船体网格数为1 475,其中首部区域网格数为575,中部网格数为600,尾部网格数为300,划分结果如图 2所示。根据船体网格的划分结果,计算船长方向的网格长度的最小值,将计算的时间步长设为0.01 s。

|
图 2 船体网格划分 Fig. 2 Hull mesh of the model |
自由面网格根据船体水线处网格大小向外辐射划分,如图 3所示。整个自由面计算域半径为5倍的船长,网格长度沿径向逐渐增大。

|
图 3 自由面网格划分 Fig. 3 Free surface mesh |
对于线性的耐波性数值预报,主要采用基于Salvese等[15]提出的线性切片理论计算有航速船舶的纵摇和垂荡耦合运动响应,使用已有软件进行。
将DTMB5512船体曲面进行等分片体切割,选择线性切片理论进行顶浪航行耐波性预报。为了提高计算精度,将船体曲面切成70个剖面,如图 4所示。采用Lewis保角变换法对各剖面进行变换,系数取为12。

|
图 4 船体切片三维图 Fig. 4 3-D model of hull after slicing |
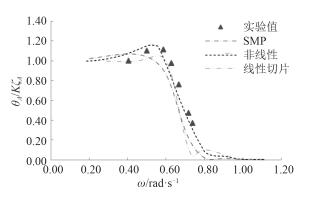
将WASIM计算的船舶在波浪中的非线性运动响应进行傅里叶变换,得到相应的传递函数,并与按线性切片法计算的结果以及模型试验的结果进行对比,如图 5~图 8所示。图中ZA表示船体垂荡运动的幅值,θA表示船体纵摇运动的幅值,ζA表示船体遭遇的波幅,K表示遭遇波的波数,ω表示相应波浪的圆频率。

|
图 5 垂荡传递函数(Fn=0.34) Fig. 5 Heave RAO(Fn=0.34) |
|
图 6 纵摇传递函数(Fn=0.34) Fig. 6 Pitch RAO(Fn=0.34) |
|
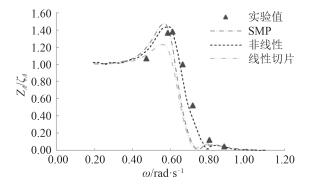
图 7 垂荡传递函数(Fn=0.41) Fig. 7 Heave RAO(Fn=0.41) |
|
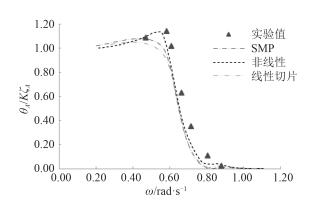
图 8 纵摇传递函数(Fn=0.41) Fig. 8 Pitch RAO(Fn=0.41) |
求对比分析以上传递函数曲线图中的4种计算结果,在相同的航速下,对于同一种运动响应,采用基于三维非线性时域势流理论计算的传递函数,比线性切片法和SMP法计算的结果更接近试验值。主要体现在:
1) 当波浪频率较高的时候,即频率为0.6~1.1时,此时传递函数曲线处于下降阶段,非线性计算值与试验值的误差约为2%~12%,而线性切片计算结果与试验值误差达8%~17%。
2) 从图中可以看出,非线性计算的传递函数曲线的峰值与试验峰值误差约为3%~8%,而线性方法计算的峰值与试验峰值误差约为5%~12%;同时非线性峰值对应的频率与试验峰值对应的频率误差约为1%~6%,而切片法的误差达9%~19%。由此得出非线性计算结果的峰值以及对应的频率与试验值更吻合。
3) 非线性方法计算得到的传递函数曲线走势与试验结果趋于一致。
因此,采用WASIM软件可以较为准确地预报有航速船舶在波浪中的非线性运动响应,该方法的预报值比线性切片理论的计算结果更能反映船舶摇荡的真实情况。
4 结语在大幅波浪中航行的船舶,船体与波浪的相互作用十分剧烈,其运动具有明显的非线性特点,所以针对恶劣海况中高航速下的船体砰击载荷预报,一般采用“两步走”的方法,即在计算船体运动响应的基础上进行砰击载荷预报,因此为了使计算的船体砰击压力更具合理性,必须准确预报波浪中船体的摇荡运动。
基于三维时域势流理论的WASIM软件不仅能够计及流场压力计算式中的速度二次项、瞬时湿表面变化等非线性影响因素,还能计及任意航速效应的影响,与线性切片方法相比,该方法计算得到的结果更能体现船体摇荡的实际情况,更具合理性和准确性[9]。虽然该计算方法需要的计算资源相对更多、计算时间更长,但是随着现代计算机技术的突飞猛进的发展和船舶设计要求的不断提高,采用基于三维非线性时域势流理论预报船舶耐波性的方法将会得到更好更广泛的应用。
| [1] | 黄文波.船舶结构可靠性载荷概率组合分析[D].上海:上海交通大学, 2001. |
| [2] | 戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007 . |
| [3] | 赵路.计及操纵性效应的船舶运动与波浪载荷计算[D].哈尔滨:哈尔滨工程大学, 2008. http://cdmd.cnki.com.cn/article/cdmd-10217-2009060131.htm |
| [4] | 刘昌凤.波浪作用下三维物体大振幅运动问题的时域数值研究[D].大连:大连理工大学, 2013. http://cdmd.cnki.com.cn/article/cdmd-10141-1013198561.htm |
| [5] | 唐坤.军辅船入级船体结构强度评估方法研究[D].哈尔滨:哈尔滨工程大学, 2009. http://cdmd.cnki.com.cn/article/cdmd-10217-2010074679.htm |
| [6] | 张金亮.迎浪状态下高速双体船的运动响应计算[D].天津:天津大学, 2007. http://cdmd.cnki.com.cn/article/cdmd-10056-2008186145.htm |
| [7] | 杨奕.船舶运动预报方法研究[D].哈尔滨:哈尔滨工程大学, 2005. http://cdmd.cnki.com.cn/article/cdmd-10217-2005137062.htm |
| [8] | 李学菊.基于Rankine源的舰船波浪载荷时域计算方法研究[D].哈尔滨:哈尔滨工程大学, 2009. http://cdmd.cnki.com.cn/article/cdmd-10217-2010075152.htm |
| [9] | 张海彬, 赵耕贤. 水动力分析在海洋结构物设计中的应用[J]. 中国海洋平台 , 2008, 23 (1) :1–6. |
| [10] | 姬广令.用边界元方法对构件附加水质量的研究[D].天津:天津大学, 2006. http://cdmd.cnki.com.cn/article/cdmd-10056-2008184443.htm |
| [11] | 郭宇. LNG船运动与载荷计算方法研究[D].哈尔滨:哈尔滨工程大学, 2010. http://cdmd.cnki.com.cn/article/cdmd-10217-1011019768.htm |
| [12] | 陈胜男.超大型集装箱船砰击载荷研究[D].哈尔滨:哈尔滨工程大学, 2012. http://cdmd.cnki.com.cn/article/cdmd-10217-1012517397.htm |
| [13] | DNV Software. WASIM Theory Manual[Z]. 2011. |
| [14] | IRVINE JR M, LONGO J, STERN F. Pitch and heave tests and uncertainty assessment for a surface combatant in regular waves[J]. Journal of Ship Research , 2008, 52 (2) :146–163. |
| [15] | SALVESEN N, TUCK E O, FALTINSEN O. Ship motions and sea loads[J]. Transactions Society of Naval Architects and Marine Engineers , 1970, 78 :250–287. |
 2016, Vol. 38
2016, Vol. 38
