2. 大连测控技术研究所, 辽宁 大连 116013
2. Dalian Scientific Test and Control Technology Institute, Dalian 116013, China
围壳结构是水下航行器突出于艇体整体线型最大的结构,在其内部布有通气管、潜望镜和通信天线等各类装置,是航行、观测及指挥的重要场所[1]。围壳结构在流体冲击的作用下会向外辐射噪声,其量值水平对于艇体结构来说非常的重要,一直以来都是学者们研究的重点内容。
从减振降噪角度来说,对围壳结构线型进行优化设计可以减少流体与结构体作用产生的噪声,洪祥武等[2]从围壳流场压力特性出发,对围壳开孔结构进行了分析研究;郑杨等[3]针对围壳头部线型结构进行了优化分析;杜波等[4]通过仿真数值计算对围壳顶部阻力和压力进行了分析,得出了一些结构曲率变化对辐射噪声的影响结果,以上的研究结果表明,优化后的围壳结构可以有效降低辐射噪声。
流噪声和流激噪声的主要区别在于,前者噪声源主要是结构体周围流场,而后者的噪声源则是流场脉动压力激励下的结构响应。因此后者属于动力学分析范畴,动力学分析主要研究的是结构体的动态性能。江文成[5]通过对标准模型水下航行器流噪声和流激噪声进行计算得出流激噪声在全频带内声级平均要高出流噪声 6~10 dB。因此,针对于围壳结构进行流激噪声方面的研究是非常重要的。
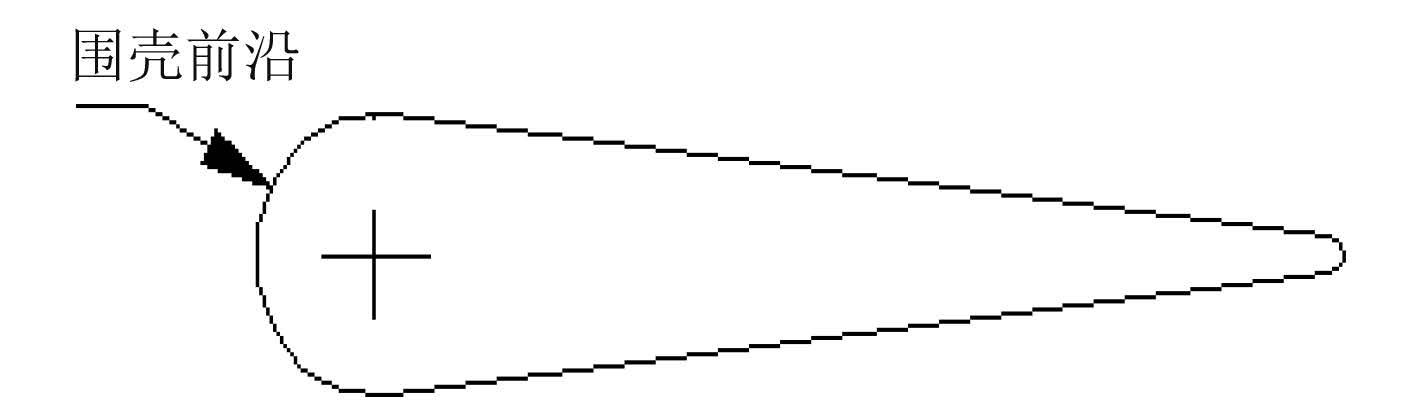
艇体围壳不是绝对的刚体,而是在激励作用下会产生位移的弹性体,因此,对流激噪声进行数值研究归根结底是流固耦合问题,在计算的双方程结果中,位移[5]和加速度为最终输出。本文利用建模软件,建立标准的围壳结构模型,垂向 CAD 效果图如图 1 所示,模型包括结构前沿,角度渐变区域以及整体线型,整体尺寸是文献[1]数值计算模型的 50 倍。计算材料选为结构钢,流体材料为海水。
|
图 1 围壳垂向 CAD 效果 Fig. 1 Vertical result effect of the sail |
在已有理论研究的基础上,本文基于 Ansys 与 Virtual lab 软件平台,综合运用有限元和边界元方法,开展数值仿真计算研究,通过对初始流速 6 kn、增速为 8 kn、高度增加 2 m 及纵向长度增加 2 m 等不同条件下的仿真计算,可以得到一些有意义的结论,为水下航行器流激围壳优化设计提供了理论参考,具有一定的工程应用价值。
1 围壳结构模态分析动力学分析的 2 个基本特征分别是结构体的自由振动和强迫振动,自由振动强调的是结构本身的固有特性,包括固有频率、模态阵型等。其基础是动力学方程:
| $ { M}\mathop \delta \limits^{..} + { C}\mathop \delta \limits^. + { K}\delta = { F}\text{。} $ | (1) |
式中:$\mathop \delta \limits^{..} $ 和 $\mathop \delta \limits^. $ 分别为系统的节点加速度矢量和速度矢量;M,C,K,F 分别为系统的质量矩阵,阻尼矩阵、刚度矩阵和节点载荷矢量。当载荷不存在时,则该方程就变为固有频率动力学计算方程。
本文对 1 000 Hz 以下结构固有频率进行计算。通过计算可知,初始结构,计算至 1 452 阶达到 1 000 Hz,高度增加 2 m,需要 1 650 阶,长度增加 2 m,则需要 1 740 阶。此计算结果体现出不同结构下的固有状态的不同。模态计算结果将作为动力学计算的先验条件施加至后续计算当中。图 2给出初始结构第 1 阶 3.8 Hz 阵型图。

|
图 2 初始结构第 1 阶阵型 Fig. 2 First formation of original structure |
动力学输入激励为流体脉动压力,采用流体软件 Ansys-CFX 可以对结构体包络流场脉动压力进行数值计算。在有限元程序中,利用 CFD(计算流体力学)动量方程、能量方程和质量方程[6]结合相应的理论及算法可以完成对结构体周围流场信息的计算。
本文的模拟研究,采用 κ-ε 湍流模型,κ-ε 模型适合绝大多数的工程湍流模型,其中 κ 为湍流动能,定义为速度波动的变化量,单位 m2/s2。ε 为湍流动能耗散,即速度波动耗散的速率,表征单位时间湍流动能。
κ-ε 模型在系统方程里引入了 2 个新变量。流体连续方程为:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho {{U}}} \right) = 0\text{,} $ | (2) |
式中:ρ 为流体的密度,U 为速度值,动量方程为
| $ \frac{{\partial \rho {{U}}}}{{\partial t}} \!+\! \nabla \cdot \left( {\rho {{U*U}}} \right) \!-\! \nabla \cdot \left( {{\mu _{{\rm{eff}}}}\nabla {{U}}} \right) \!=\! \nabla \cdot {\rm{p' \!+\! }}\nabla \cdot {\left( {{\mu _{{\rm{eff}}}}\nabla {{U}}} \right)^{\rm{T}}} \!+\! {\rm{B}}\text{,} $ | (3) |
式中:B 为体积力和;μeff 为有效黏度;p' 为修正压力。
有效黏度可以通过 κ 和 ε 来表示,即
| $ {\mu _{{\rm{eff}}}}{\rm{ = }}\mu + {{{C}}_\mu }\rho \frac{{{{{K}}^2}}}{\varepsilon }\text{,} $ | (4) |
k 和 ε 的值可以通过湍流动能方程求解,湍流动能方程和耗散率方程分别为
| $ \begin{array}{l} \displaystyle\frac{{\partial \left( {\rho {\rm{k}}} \right)}}{{\partial t}} \!+\! \nabla \cdot \left( {\rho {{U_k}}} \right) \!=\! \nabla \cdot \left[{\left( {\mu \!+\! \frac{{{\mu _{\rm{t}}}}}{{{\sigma _{\rm{k}}}}}} \right)\nabla {{k}}} \right] + {{{P}}_{{k}}} - \rho \varepsilon \text{,}\\ \displaystyle\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}}\!\!+\!\! \nabla \!\!\cdot\!\! \left( {\rho {{U}}_\varepsilon } \right) \!\!=\! \!\nabla \!\!\cdot\!\! \left[{\left( {\mu \!\!\!+\!\! \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\!\!\nabla \varepsilon } \right] \!\!+\!\! \frac{\varepsilon }{{{k}}}\left( {{{{C}}_{{\varepsilon _1}}}{{{P}}_{{k}}} \!\!-\!\! {{{C}}_{{\varepsilon _2}}}\rho \varepsilon } \right)\text{。} \end{array} $ | (5) |
式中:${{{\rm{C}}_{{\varepsilon _1}}}}$,${{{\rm{C}}_{{\varepsilon _2}}}}$,${{\sigma _{\rm{k}}}}$和${{\sigma _\varepsilon }}$ 为常数。
在流体冲击计算过程中,k 和 ε 的值会变大[8],在本文进行流场网格划分时,不宜过于细密,否则会出现计算输出结果恶化的情况[7]。
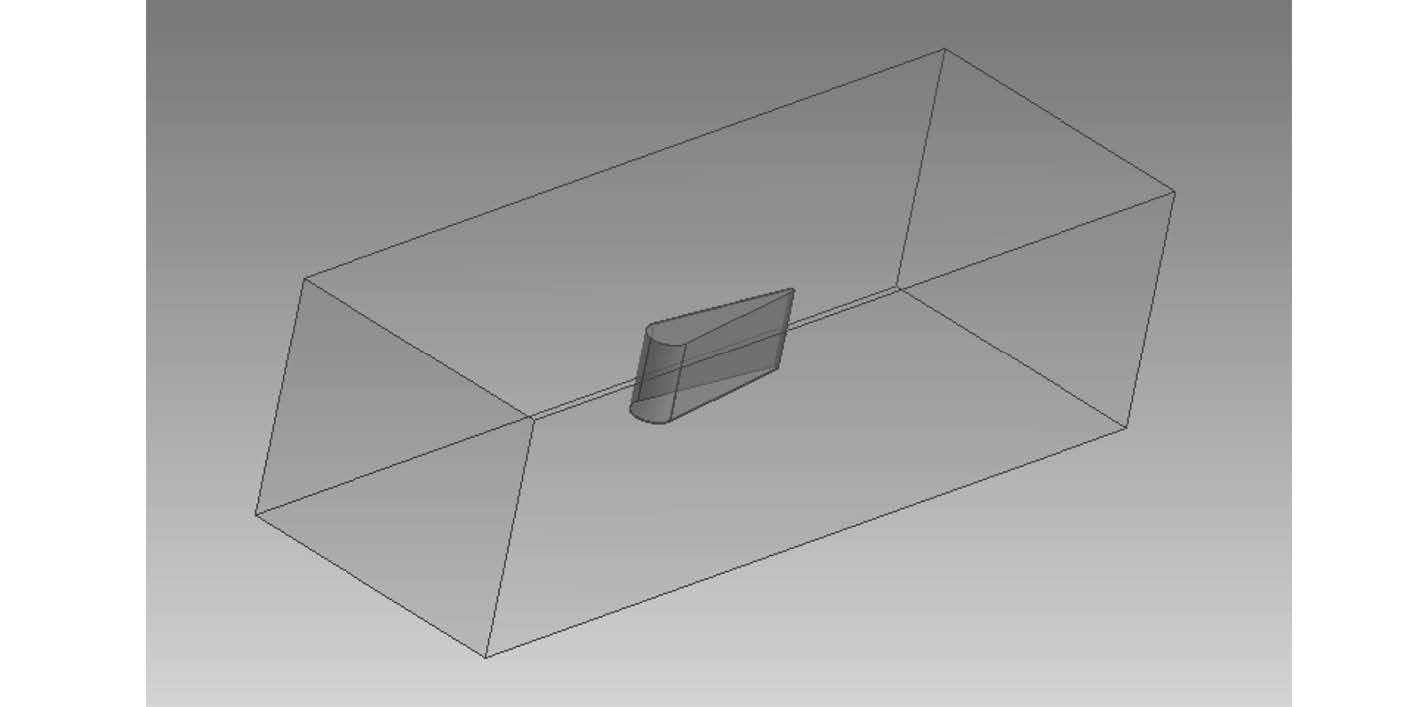
如图 3 所示,流场选择为六面体流场,流场特征尺寸为围壳结构的 3 倍,在计算当中,对围壳前对应面设置为进口面,围壳后沿对应面设置为出口面,上部设置为自由液面,两侧及底部分为壁面。在进口面设置均匀垂直的速度指向围壳,在出口面设置相对压力为 0 Pa,3 个壁面设置为无滑移条件。
|
图 3 流场搭建效果 Fig. 3 luid model effect |
采用短期 10 s 瞬态过程进行数值计算,得出随时间变化的流体载荷,图 4 为最后一个时间步围壳结构周围包络面压力云图。

|
图 4 围壳压力脉动云图 Fig. 4 Cloud picture of pressure pulsation over the sail |
从图 4 中看到,围壳结构前沿位置处脉动压力比较大,随着对称结构的展开,脉动压力值也随着降低,在流体通过前沿区域并向尾部流动的起始位置,会出现负压梯度,流速由 6 kn 增大到 8 kn,脉动压力值随着增大,负压则变小,结构变化并没有带来脉动压力上明显的差异。
将得到的围壳节点脉动压力导入动力学计算模块,便可以对流激作用下的围壳结构响应进行数值计算。
通过位移、加速度有限元方法获得的结果为单一场方程结果[9],而将脉动压力、位移、加速度三场合一的计算方法,也是流固耦合数值计算最有效的方式[10]。在同一载荷作用下,围壳不同结构状态下的响应是不同的,本质上和结构体的固有特性直接相关。
3 流激噪声数值计算将围壳结构振动响应作为边界元程序输入条件进行噪声数值计算。有限元方法着眼于全局网格划分,而边界元则只对计算体边界进行划分,在噪声计算中,需要构建相应的声场模型并进行划分。和有限元法相比,边界元法具有单元个数少,数据准备简单等特点,其对计算结构域进行面网格划分,在计算能力上,该方法存在有一些欠缺,它的应用范围以存在相应微分算子的基本解围前提,对于非均匀介质等问题难以得到有效应用,故其适用范围不如有限元广泛。并且针对边界元建立起来的求解方程系数矩阵式非对称满阵,这在一定程度上限制了解题规模。
本文的边界元程序边界元网格、声场建模如图 5 所示,声场为直径 20 m 的圆球,图中点 A 位置为声压级计算测点,将通过不同状态下该点的声压级对辐射噪声进行分析。

|
图 5 边界元网格及声场建模效果 Fig. 5 BEM mesh and the acoustic model effect |
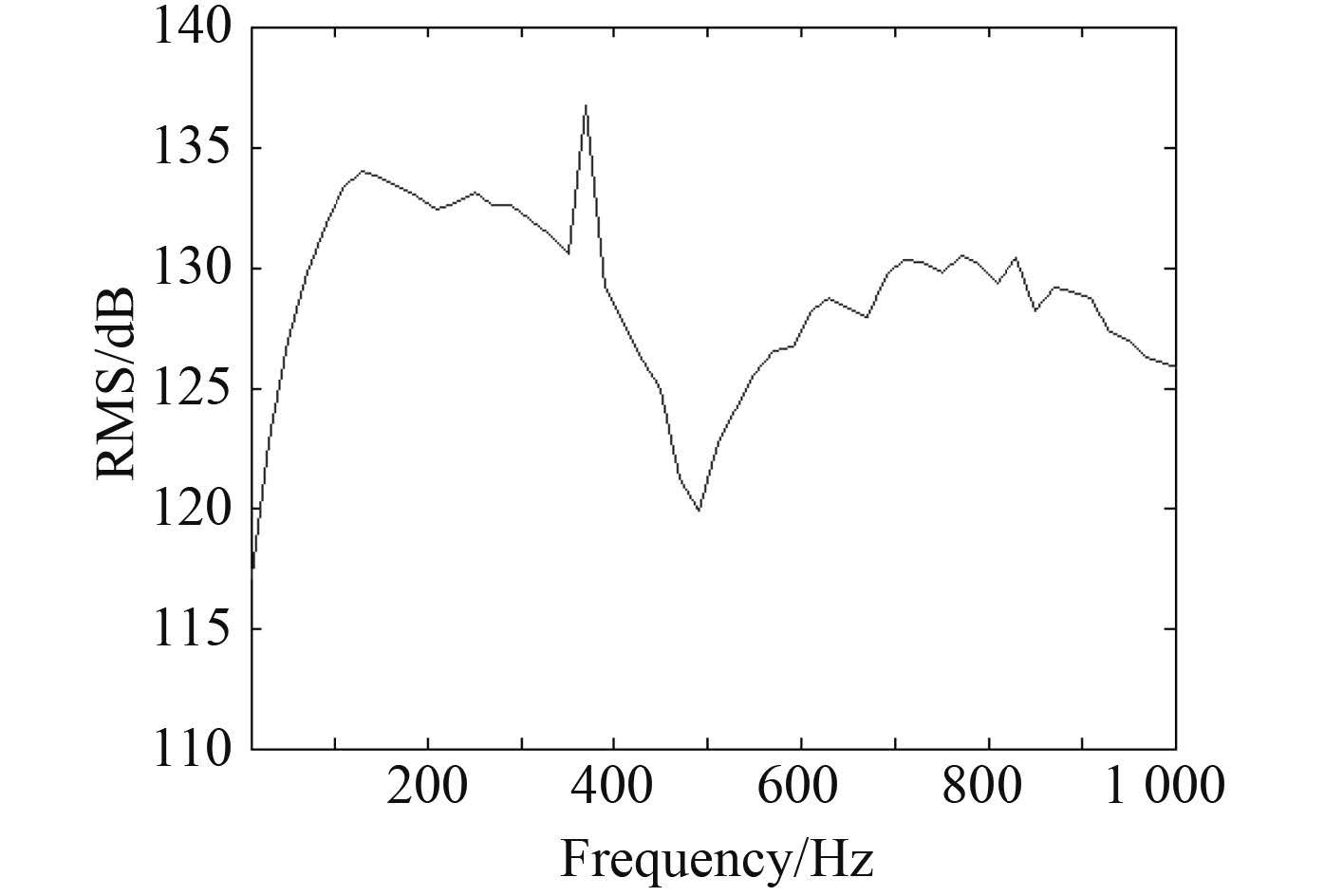
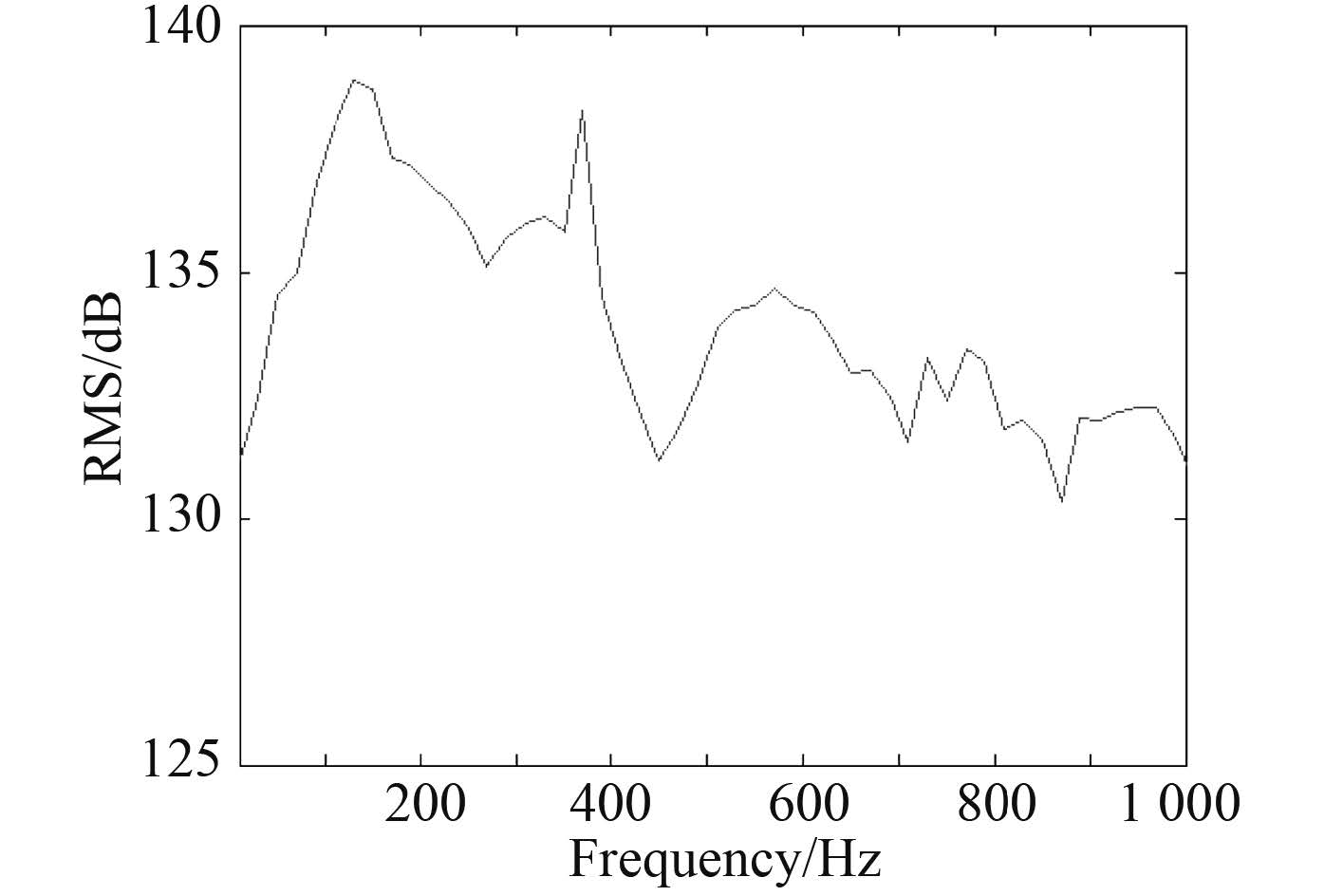
对 1 000 Hz 频带内均匀选择 50 个频点进行计算可以得出指定测点声压级,图 6~图 9 分别给出初始 6 kn 工况、8 kn 工况、变高结构以及纵向变长结构状态下指定测点的声压级。
|
图 6 初始 6 kn 测点声压级 Fig. 6 SPL of the specific measure point with original 6 knots |
|
图 7 增速至 8 kn 测点声压级 Fig. 7 SPL of the specific measure point with speeding up to 8 knots |
|
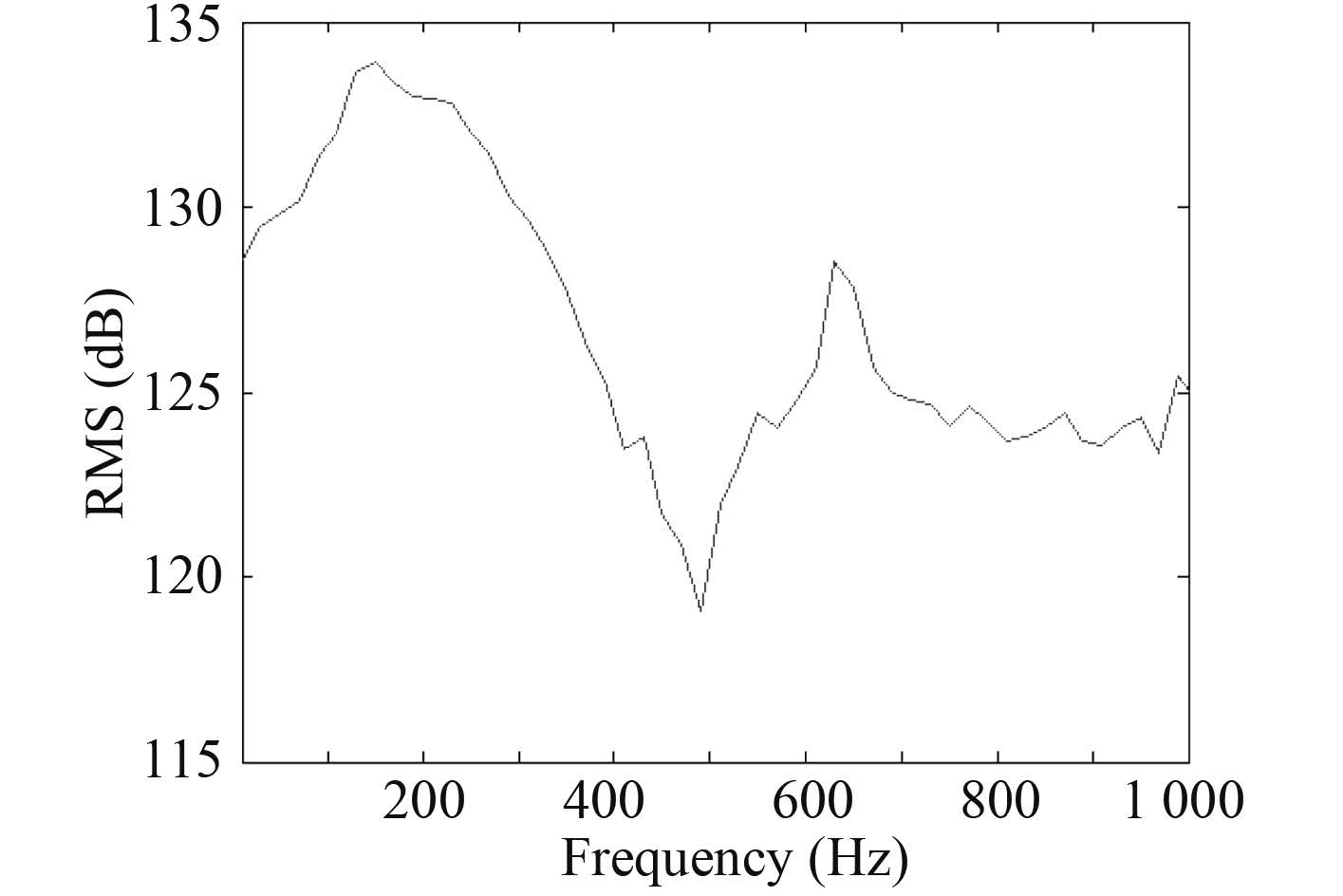
图 8 增高 2 m 测点声压级 Fig. 8 SPL of the specific measure point with height increasing 2 meters |
|
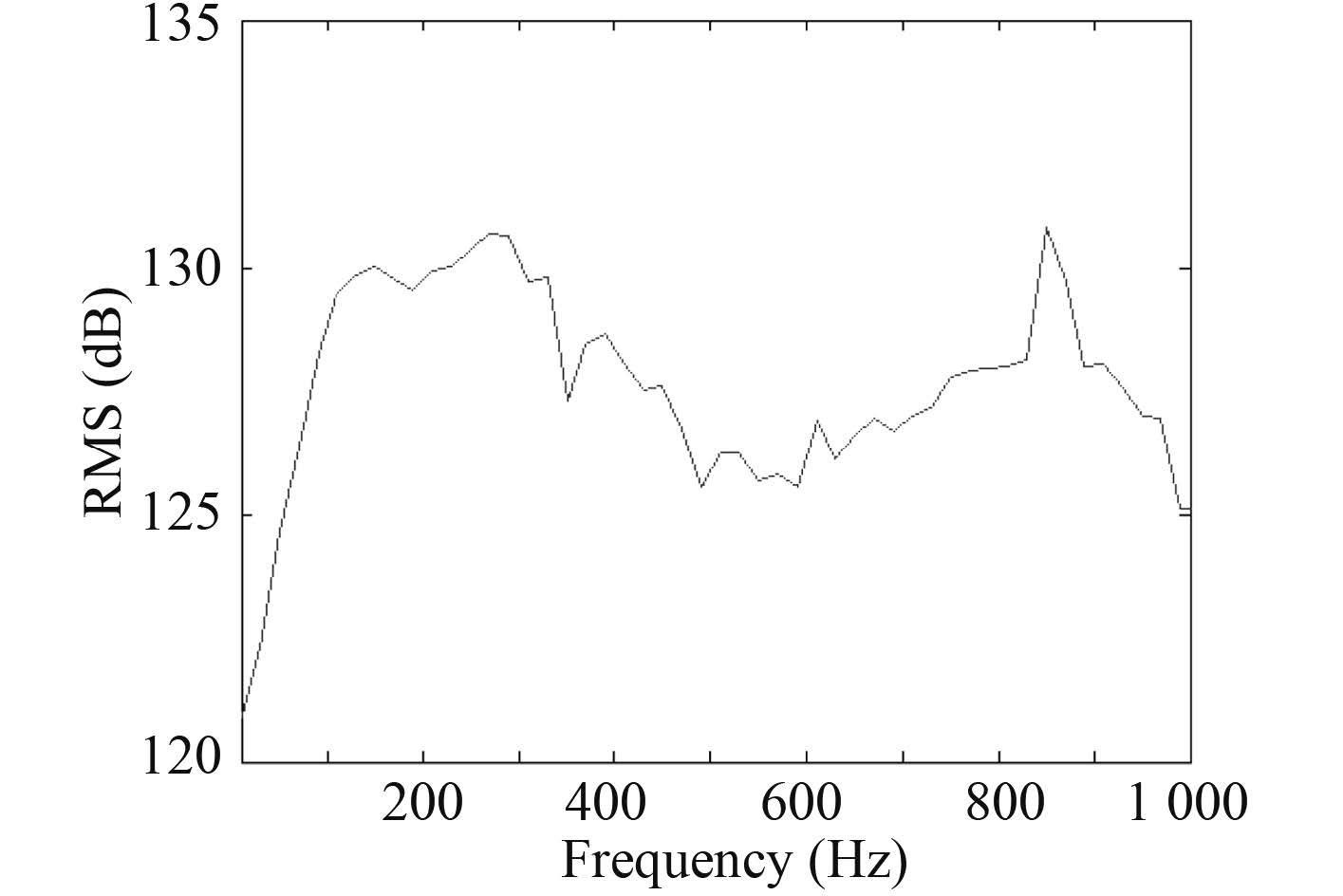
图 9 增长 2 m 节测点声压级 Fig. 9 SPL of the specific measure point with length increasing to 2 meters |
从指定场点声压级变化曲线可以知道,整体趋势上,4 种状态下低频辐射噪声随着频率的升高呈现增大的趋势,100~350 Hz 低频所引起的噪声结构响应要高于其他频带,中间频带 350~500 Hz 噪声级别则较低。该计算结果与文献[1]中小尺度模型计算结果非常接近,与该文献中的试验值对比,计算频带内的流激噪声量值要高于水动力噪声。
当速度由 6 kn 增至 8 kn 时,全频带总声级会随之升高,通过比较可知,1 000 Hz 频带以内平均升高近 10 dB。高速状态下高频范围内噪声的极大极小值脉动性也要更加剧烈一些。基础结构下,比较模态结果可知,在 372.32 Hz 下,流激激励所引起的结构振动变化最大。
当围壳增加 2 m 时,共振点变为 632.45 Hz。低频段量值略高,并且变化趋势要缓于初始结构,高频段声级低于初始状态,总声级量值与初始状态差别不大,极小值点与初始工况不同,200~400 Hz 的渐进减小趋势比较明显。
当围壳纵向长度增加 2 m 时,中频段噪声相比于其他工况要高,并且变化趋势较缓,共振点变为 867.58 Hz。总声级与初始状态差别不大。和文献[5]中单独计算围壳的模块进行对比可知,围壳结构流激噪声的量值要略高于水动力噪声,在相对中、高频段与水动力噪声的变化趋势也有区别。
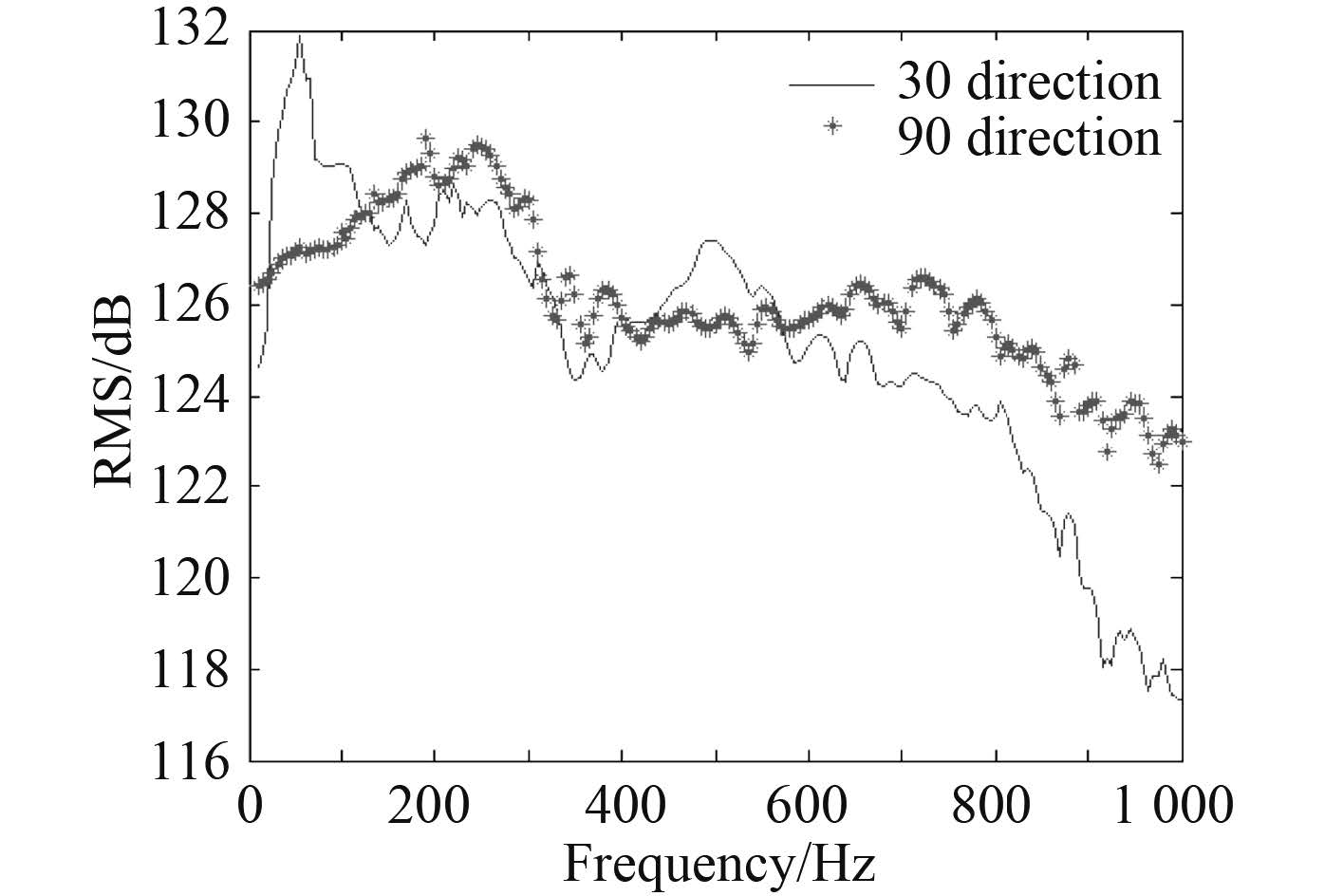
图 10 给出了围壳不同迎流方向上的测点声压级,分别给出了与来流方向夹角为 30°和 90°条件下的计算结果,结合图 8 初始工况计算结果,经对比分析,可知:相比于初始工况,当围壳面向 30°来流时,低频的噪声级比较高,并且其相对高频段的声级要高于 90°方向来流,在流向不是通过流线型的 0°角方向时,低频噪声均低于初始工况。
|
图 10 不同流向条件下的测点声压级 Fig. 10 SPL of the different flow conditions |
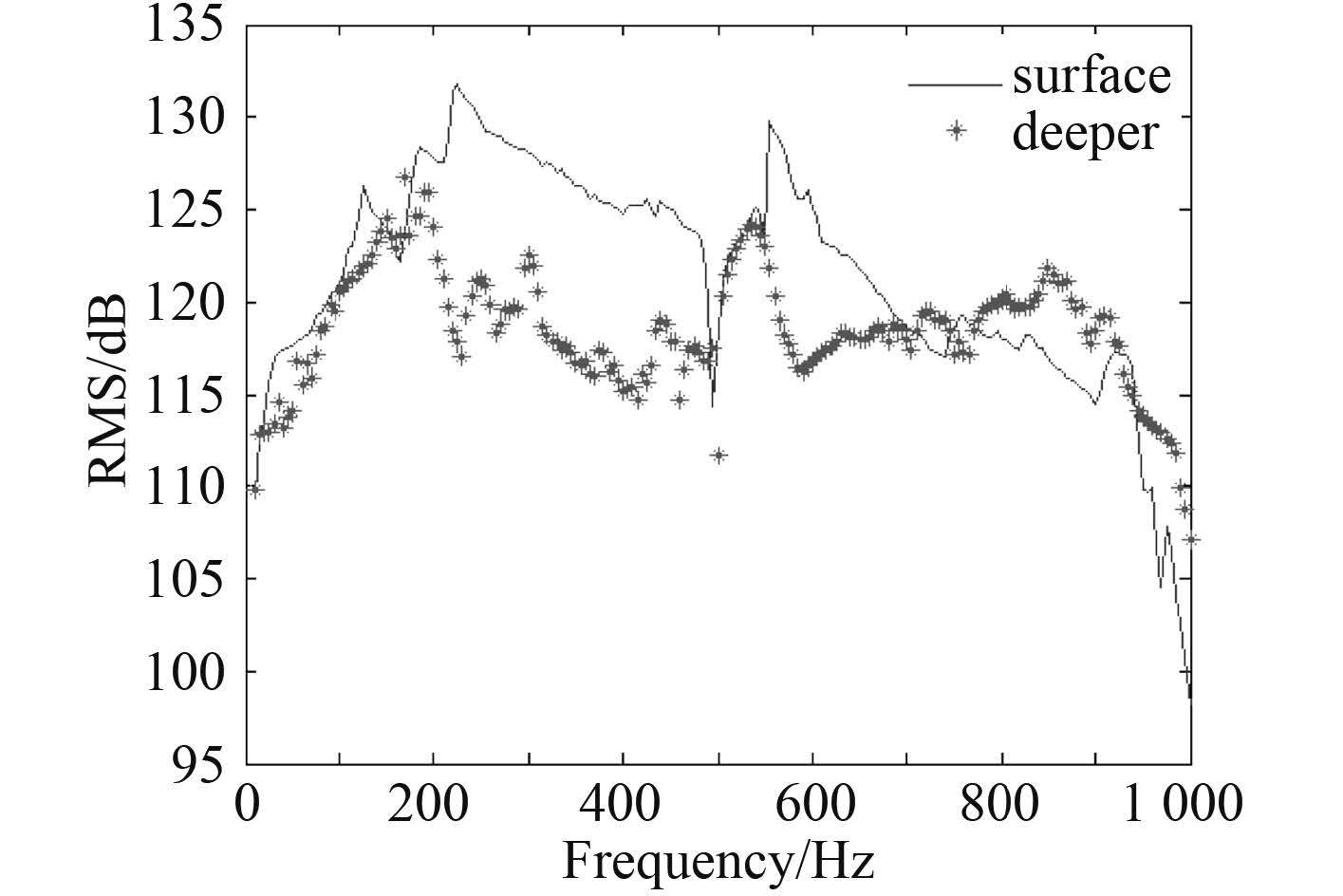
图 11 给出了围壳近水面(深度约 5 m)和水下 10 m 时的声压级计算结果,结合图 8 初始工况计算结果可知:相比于初始工况,深度 5 m 和 10 m 下的声压级均较小,其中围壳接近水面工况高于深度 10 m 处的噪声级,说明随着潜深的增加,围壳噪声级存在逐渐降低的趋势。
|
图 11 不同深度下的测点声压级 Fig. 11 SPL of the different depth conditions |
通过对不同状态下围壳周围流场信息及辐射噪声数值仿真,可以得到如下结论:
流速升高,可以引起围壳结构周围流体脉动压力及辐射噪声的升高;围壳高度增加低频段辐射噪声相对较高,围壳纵向长度增加可以提高中频段辐射噪声量值,且随着围壳高度和长度的增加,引起的共振频率升高;随着潜深的增加,围壳噪声级存在逐渐降低的趋势。
本文的数值计算及相应结论为更深层次流激围壳噪声特性研究提供了相关思路,当进行围壳结构设计以及航行时,应该兼顾使用效果及噪声水平,合理选择机动过程、合理设计围壳结构,从而达到通过优化实际作战及工程建造来进行合理减振降噪的目的。
| [1] | 侯本龙. 围壳结构流激振动噪声特性研究[D]. 哈尔滨:哈尔滨工程大学, 2011. |
| [2] | 聂毅, 余雄庆. 翼面隐身结构优化设计[J]. 南京航空航天大学学报 , 2008, 40 (4) :465–468. |
| [3] | 郑杨. 围壳结构声辐射机理研究[D]. 哈尔滨:哈尔滨工程大学, 2009. |
| [4] | 江文成. 潜艇流噪声与流固耦合作用下流激噪声的数值模拟[D]. 上海:上海交通大学, 2013. |
| [5] | OLSON L G, BATHE K J. A study of displacement-based fluid finite elements for calculating frequencies of fluid and fluid-structure systems[J]. Nuclear engineering and design , 1983, 76 (2) :137–151. DOI:10.1016/0029-5493(83)90130-9 |
| [6] | PETYT M, LEA J, KOOPMANN G H. A finite element method for determining the acoustic modes of irregular shaped cavities[J]. Journal of sound and vibration , 1976, 45 (4) :495–502. DOI:10.1016/0022-460X(76)90730-6 |
| [7] | 王福军. 计算流体力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004 . |
| [8] | SANDBERG G, GÖRANSSON P. A symmetric finite element formulation for acoustic fluid-structure interaction analysis[J]. Journal of sound and vibration , 1988, 123 (3) :507–515. DOI:10.1016/S0022-460X(88)80166-4 |
| [9] | 杜波, 黄建伟, 陈源. 潜艇指挥室围壳顶部型线构型[J]. 船海工程 , 2007, 36 (2) :107–110. |
| [10] | BREBBIA C A. The boundary element method for engineers[M]. New York: Halstead Press, 1978 . |
 2016, Vol. 38
2016, Vol. 38
