2. 中国人民解放军 91960 部队, 广东 汕头 515000
2. No. 91960 Unit of PLA, Shantou 515000, China
目前世界范围内对潜艇通信主要采用甚低频和超低频通信方式,甚低频通信的调制方式主要采用 MSK 方式,该方式是20世纪70年代就提出的甚低频调制方式,但是该方式抗噪声和干扰能力不强,不能确保对潜艇指挥通信的连续和不间断。时频调制的 MFSK 是 IEEE 于20世纪末提出的一种新的调制方式,具有相位连续、包络恒定,频谱利用率高,特别是要求传输信号能量集中时,该方式比 MSK 更为优越,目前已应用到无线通信抗干扰的一些领域,本文对 MFSK 与传统的 MSK 甚低频通信的性能进行分析,并用实例进行比较。
1 甚低频 MSK 与 MFSK 性能仿真根据文献[1-2],在信息速率相等的条件下,MSK 的误码率与 QPSK(OQPSK)的误码率相等,也与 BPSK 的误码率相等。MSK 的误比特率公式为:
| $ {P_e} = \frac{1}{{\sqrt {2\pi } }}\int\limits_{\sqrt {\frac{{2{E_b}}}{{{n_0}}}} }^\infty {{e^{ - {{{x^2}} \mathord{\left/ {\vphantom {{{x^2}} 2}} \right. } 2}}}{\text{d}}x} = Erfc\left( {\sqrt {\frac{{2{E_b}}}{{{n_0}}}} } \right)\text{。} $ | (1) |
由于 4 个比特组成一个 16 进制的数字,所以MSK的误数字率[3-4]
| $ {P_z} = 1 - {\left( {1 - {P_e}} \right)^4} \approx 4{P_e}\text{。} $ | (2) |
用式(1)计算 MSK 的误码率,用式(2)计算 MSK 的误数字率。式(1)只能用数值方法积分。把该式写成如下形式[5-6]:
| $ \begin{array}{l} {P_e} = \displaystyle\frac{1}{{\sqrt {2\pi } }}\left( {\int\limits_0^\infty {{e^{ - {{{x^2}} \mathord{\left/ {\vphantom {{{x^2}} 2}} \right. } 2}}}{\text{d}}x} - \int\limits_0^{\sqrt {{{2{E_b}} \mathord{\left/ {\vphantom {{2{E_b}} {{n_0}}}} \right. } {{n_0}}}} } {{e^{ - {{{x^2}} \mathord{\left/ {\vphantom {{{x^2}} 2}} \right. } 2}}}{\text{d}}x} } \right) = \\[15pt] 0.5 - \displaystyle\frac{1}{{\sqrt {2\pi } }}\int\limits_0^{\sqrt {{{2{E_b}} \mathord{\left/ {\vphantom {{2{E_b}} {{n_0}}}} \right. } {{n_0}}}} } {{e^{ - {{{x^2}} \mathord{\left/ {\vphantom {{{x^2}} 2}} \right. } 2}}}{\text{d}}x}\text{。} \end{array} $ | (3) |
上式中第2项的积分上、下限都有限,故可以比较容易地进行数值积分。给定信噪比数值 Eb/n0,就可以计算出相应的误码率。计算结果表明,误比特率等于 10-4 和 10-3,需要的每比特信噪比大致等于 8.39 dB 和 6.8 dB。误数字率等于 10-4 和 10-3,需要的每比特信噪比大致等于 9.14 dB 和 7.78 dB。8.39 dB 这个数值与文献中的数值基本一致,可见这里的数值计算正确。计算结果曲线如图 1 所示。图中 x 轴所标的数字是相关器输出的信噪比,即${P_s}/{P_n} = {E_b}/{n_0}$;y 轴所标的是错误概率。图中示出2条曲线,一条是误码率(误比特率)曲线,另一条是误数字率曲线。
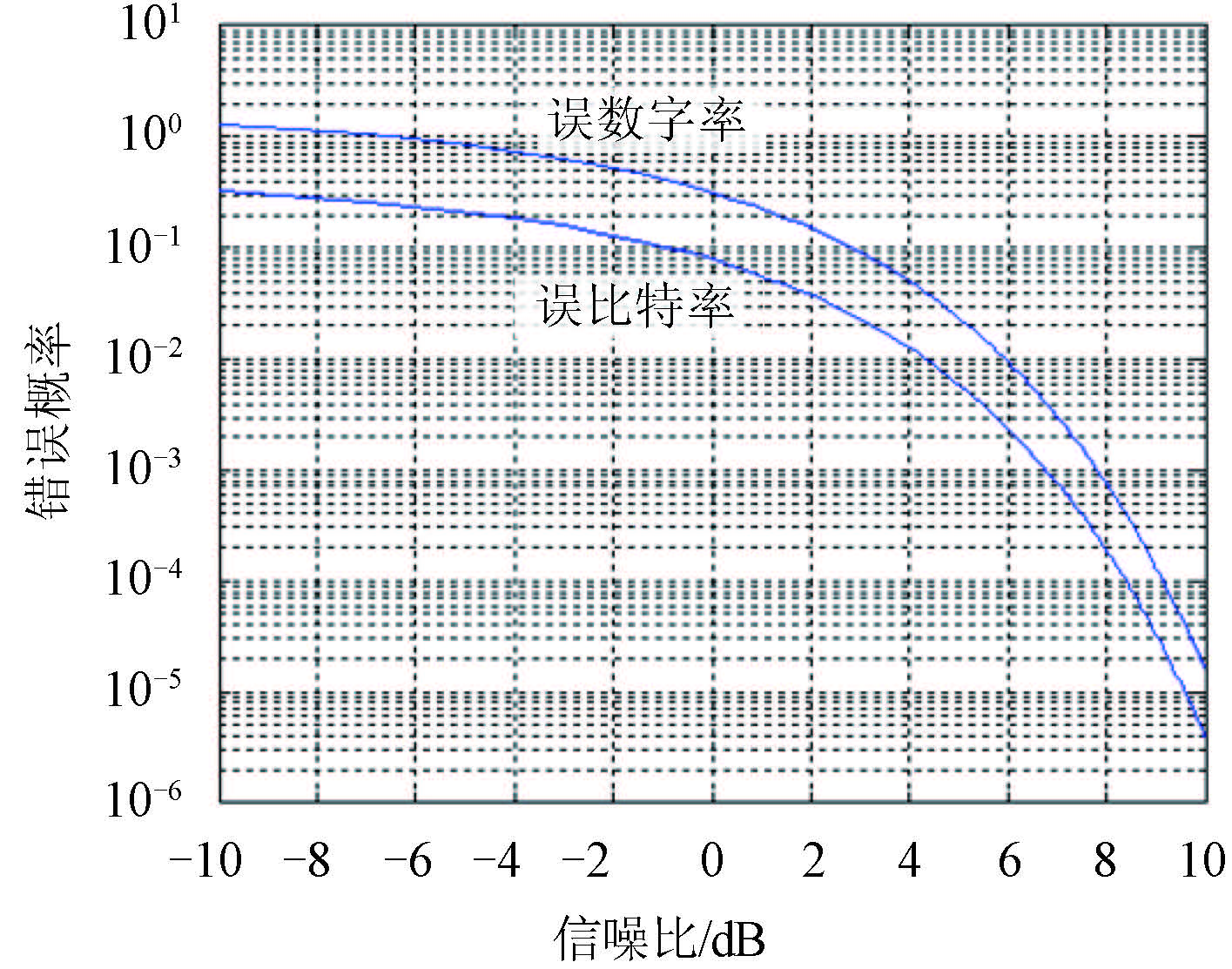
|
图 1 MSK 误码率与信噪比的关系曲线 Fig. 1 The relationship between MSK error rate and SNR |
从图 1 看出,当误码率低于 10-3~10-4 后,误码率随信噪比的增大而迅速降低,如误码率从 10-4 降至 10-5,需要增加的信噪比小于 1 dB。因此,在信息速率相等的条件下,无论是相干还是非相干 16 FSK,其误数字率均显著低于 MSK。
2 甚低频 MSK 与 MFSK 应用分析研究了 MSK 和 MFSK 的误码性能,得知在相同信息速率条件下,16 FSK 的误数字率优于 MSK 的误数字率,或者说在在相同信息速率和误数字率条件下,16 FSK 所需的发信功率小于 MSK 所需的发信功率。这是 16 FSK 调制解调体制本身拥有的优点。对于具体的甚低频通信,由于信道通频带窄,16 FSK 的信息速率必然低于 MSK 的信息速率,因此 16 FSK 所需的发信功率将进一步低于 MSK 所需的发信功率,或者在相同的发信功率下 16 FSK 的通信距离、通信深度和可靠性将高于 MSK 的通信距离、通信深度和可靠性。这是用降低通信速度换取通信距离、通信深度和通信可靠性。这在实际工作中是需要的,如在某些任务中通信距离很远,或接收区域干扰很高。
以一个 15 kHz 的甚低频信道为例,其频带宽度大致等于 55.34 Hz。根据上面的讨论,这个信道允许传输大致 75 bit/s的 MSK 调制的信号。假定在这信道内传输 50 bit/s的 MSK 信号,那么码元(比特)持续时间等于 20 ms。
在这信道内,16 FSK 的相邻频率间的最小间格频率 $ \Delta {f_{\min }} = 3.2 \ {\rm Hz} $。假定调制指数等于 1,则既可以用相干方法接收,也可以用最佳非相干方法接收。此时码元持续时间等于 312.5 ms,每比特的持续时间等于 78.125 ms。信息速率等于 12.8 bit/s。假定调制指数等于 0.5,则码元持续时间缩短为 156.25 ms,信息速率增至 25.6 bit/s;在此条件下只能用相干方法接收。
假定 QMSK 表示给定误数字率条件下 MSK 需要的信噪比。由于$ {E_b} \!=\! {P_s}{T_b} $,所以 MSK 需要的发信功率[7-9]
| $ {P_{s,MSK}} = {Q_{MSK}}{n_0}/{T_{b,MSK}} \text{。}$ | (4) |
式中$ {T_{b,MSK}} $ 为 MSK 的码元持续时间,n0 为信道的噪声功率谱密度。对于 16 FSK,其所需发信功率的公式形式同(4)。这样可得出给定误数字率条件下两种调制方式所需发信功率的比
| $ \frac{{{P_{s,16FSK}}}}{{{P_{S,msk}}}} = \frac{{{Q_{16FSK}}}}{{{Q_{MSK}}}}\frac{{{T_{b,MSK}}}}{{{T_{b,16FSK}}}} \text{。} $ | (5) |
公式右边第1项是调制解调本身带来的好处,第2项是降低通信速率换来的好处。上面已经得到误数字率 10-3 和 10-4 条件下 MSK 和 16 FSK 需要的(见表 1)。根据式(5)可以计算相干和非相干 16 FSK 和 MSK 所需通信功率的比值(见表 3)
|
|
表 1 信息速率不同条件下所需发信功率的比值 Tab.1 The ratio of transmitting power under different information rate |
表 1 的数据表明,当 MSK 的信息速率等于 50 bit/s,而 16 FSK 的信息速率等于 12.8 bit/s 时,16 FSK 所需发信功率相干接收约低 8 dB,最佳非相干接收约低 7 dB;信息速率等于 25.6 bit/s 时,16 FSK 只能相干接收,所需发信功率约低 5 dB。甚低频低端的地面上传播衰减大致为 3 dB/1 000 km 左右,所以在功率相等的条件下 12.8 bit/s 速率的 16 FSK 的通信距离可以比 50 bit/s 速率的 MSK 增加 2 000~3 000 km。甚低频低端电磁波在海水中的衰减大约每米 4~5 dB,因此在相同通信距离条件下,12.8 bit/s 速率的 16 FSK 的通信深度比 50 bit/s 速率的 MSK 深 1~2 m。从相干 16 FSK 的误码率和最佳非相干 16 FSK 的误码率看出,在低误码率条件下,误码率降低一个数量级所需增大的信噪比不到 1 dB。总的结论是:采用较低速率的 16 FSK 比采用 MSK 在通信距离、深度和可靠性方面都有很大的好处,这在实际的对潜通信中很有必要。
3 结 语对甚低频通信的 16 FSK 和 MSK 方式从误码率、发信功率等多方面进行比较分析,得出了采用 16 FSK 通信制式,可以用其本身的优点及降低通信速率换取通信距离、深度和质量的结论,为对潜通信的大深度、远距离的调制选型评估提供了科学、合理的理论支撑。
| [1] | 潘威炎. 长波超长波极长波传播[M]. 成都: 电子科技大学出版社, 2004 . |
| [2] | TRANTER W H, SHANMUGAN K S, RAPPAPORT T S, et al. Principles of communication systems simulation with wireless applications[M]. New York: Pearson Education, 2004 . |
| [3] |
孟庆辉, 王永斌, 赵志礼. 潜艇周围影响超低频通信的电磁噪声来源及特征分析[J]. 舰船科学技术 , 2009, 31 (11) :66–69.
MENG Qing-hui, WANG Yong-bin, ZHAO Zhi-li. The source and characteristics of extremely low frequency noise affecting communications around the submarine[J]. Ship Science and Technology , 2009, 31 (11) :66–69. |
| [4] |
李光明, 宋裕农, 蔡广友. 甚低频通信信道建模与仿真[J]. 通信技术 , 2010, 43 (6) :41–42.
LI Guang-ming, SONG Yu-nong, CAI Guang-you. Modeling and simulation of VLF channel[J]. Communications Technology , 2010, 43 (6) :41–42. |
| [5] |
张俊昌, 曹海鹏, 谢家祥. 甚低频对潜通信数据压缩编码技术研究[J]. 通信技术 , 2008, 41 (12) :262–264.
ZHANG Jun-chang, CAO Hai-peng, XIE Jia-xiang. Research of data compress and encoding technique in VLF communication for submarine[J]. Communications Technology , 2008, 41 (12) :262–264. |
| [6] |
张文娟, 王永斌, 付天晖. 甚低频/低频通信中大气噪声仿真研究[J]. 舰船电子工程 , 2006, 26 (6) :123–126.
ZHANG Wen-juan, WANG Yong-bin, FU Tian-hui. Simulation study on atmospheric noise in VLF/LF communication[J]. Ship Electronic Engineering , 2006, 26 (6) :123–126. |
| [7] |
付贞, 温东, 姜波, 等. 甚低频大气噪声中的MSK通信系统仿真[J]. 舰船电子工程 , 2010, 30 (1) :98–101.
FU Zhen, WEN Dong, JIANG Bo, et al. Simulation of MSK communication system in VLF atmospheric noise[J]. Ship Electronic Engineering , 2010, 30 (1) :98–101. |
| [8] |
任席闯, 左丽芬, 李树明, 等. 基于GIS的超低频通信服务区的预测[J]. 舰船科学技术 , 2013, 35 (4) :117–119.
REN Xi-chuang, ZUO Li-fen, LI Shu-ming, et al. The prediction of SLF communication coverage based on GIS[J]. Ship Science and Technology , 2013, 35 (4) :117–119. |
| [9] | MALLIK R K, GOGOI A K. An optimum detector for coherent M-ary signaling in the presence of impulsive noise[C]//Proceedings of the 2000 IEEE international conference on personal wireless communications. Hyderabad:IEEE, 2000:363-367. |
 2016, Vol. 38
2016, Vol. 38
