2. 中国舰船研究设计中心, 湖北 武汉 430064
2. China Ship Research and Design Center, Wuhan 430064, China
频率选择表面是一种周期性单元构成的复合结构材料,对于照射到这种材料上的电磁波而言,其具有空间滤波特性,包括低通、高通、带通和带阻滤波特性。上述特性导致其被广泛应用于宽带通信,雷达系统及天线技术[1-3]。
目前,用于分析频率选择表面的传输特性,可以采用的电磁仿真工具包括有限元方法、有限差分法以及矩量法等。尽管这些仿真软件能够精确对频率选择表面的传输特性进行仿真计算,但是这些方法需要消耗较长的计算时间,而且设计者在使用这些工具进行频率选择表面结构设计时,无法对周期单元的内在设计规律进行较好的掌握,导致周期单元的设计过程十分漫长。而频率选择表面等效电路模型方法[5]能够有效克服上述问题,可以利用简单的仿真模型非常快速对一定结构的频率选择表面的传输特性进行计算,虽然这种简易模型的计算精度无法达到电磁仿真软件的计算精度,但是能够使设计者非常快速地掌握各尺寸参数对频选表面传输特性的影响规律。
利用本文提出的小型频率选择表面结构设计方法及等效电路模型,能够更加直观地掌握频选表面的设计规律。目前,该等效电路模型设计方法将在多层频率选择表面的设计过程中开展应用。
1 等效模型方法与电磁仿真计算不同,等效电路模型为频率选择表面传输特性的计算提供了一种简易的计算方法,这种方法首先将电磁波照射到频率选择表面的耦合过程等效为一种传输线模型,然后利用传输线分析方法将频率选择表面周期单元结构内的不同子结构等效为集总参数电容或电感的串并联。该模型首先由 Markowitz 和 LEE[5]提出,给出了电磁波垂直照射频率选择表面时,周期性水平长金属线和垂直长金属线在不同极化电磁波照射下的集总参数等效模型。
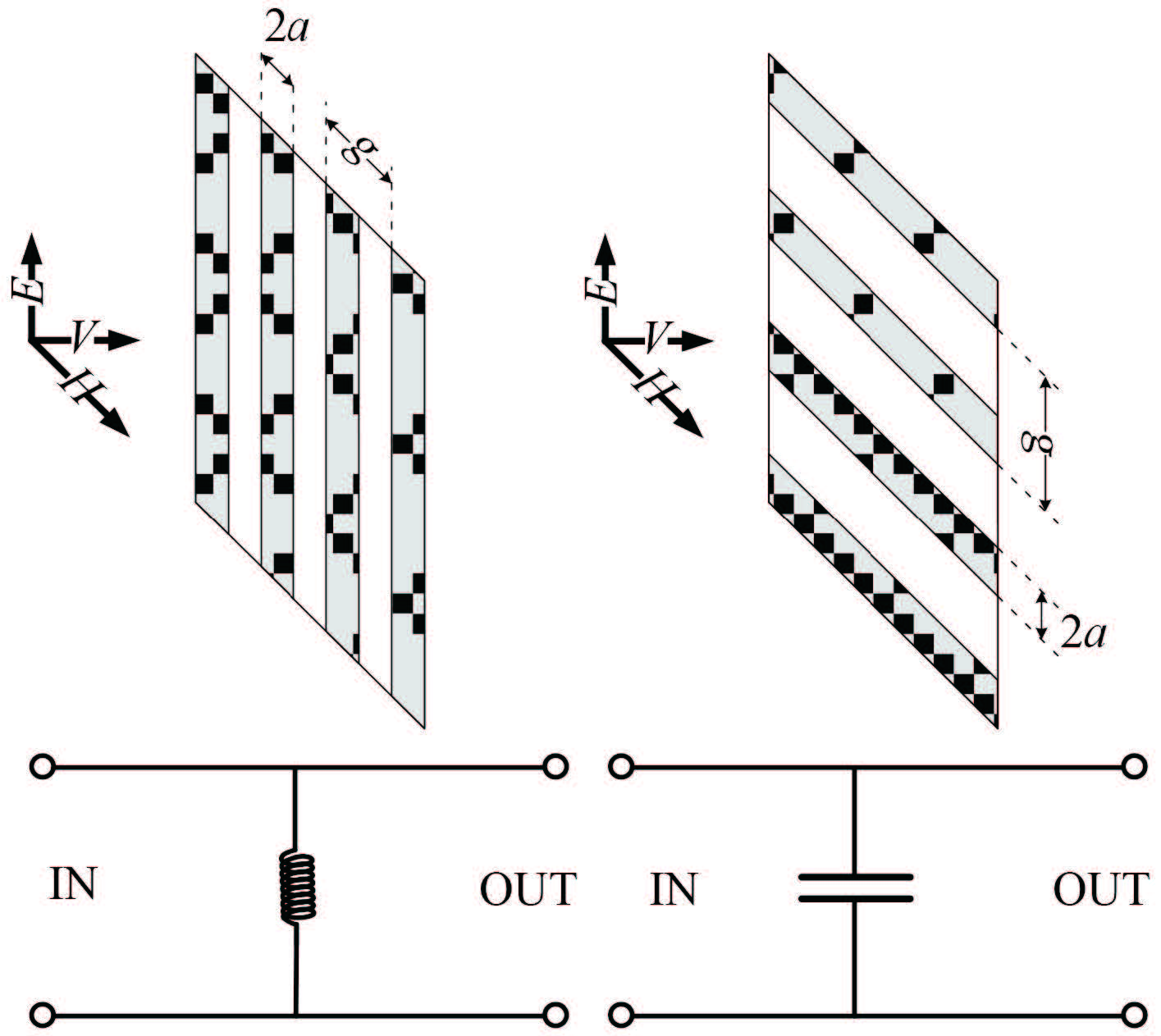
采用传输线分析方法对电磁波与频率选择表面相互作用进行分析可知,该作用过程可以等效为集总电容、电感对传输线能量进行耦合的过程。例如,对于周期性金属细线构成的无限大平面,当该平面厚度相对于波长较小时,对于不同极化方向的垂直入射电磁波而言,这些带线的等效电路分别为电感和电容,取决于电场方向是否与带线平行,如图 1所示。Markowitz 给出了其周期性金属线结构的并联电感或并联电容值的大小(取决于电场是否与带线平行)。
|
图 1 不同极化方式下周期性长带线的等效集总参数模型 Fig. 1 The equivalent lumped parameter model of periodic strapline under different polarization |
归一化并联电感值为:
| $ \begin{array}{l} {X_{TE}}{ = ^{w.L}}{/_{{Z_o}}} = \\[10pt] \displaystyle\frac{{p.\cos (\theta )}}{\lambda }.({\rm ln}({\rm cosec}\pi w/2p)) + G(p,w,\lambda ,\theta ))\text{;} \end{array} $ | (1) |
归一化并联电容值为:
| $ \begin{array}{l} {B_{TE}}{ = ^{w.C}}{/_{{Y_o}}} = \\[10pt] \displaystyle\frac{{4.p.\sec (\theta )}}{\lambda }.({\rm ln}({\rm cosec}(\pi g/2p)) + G(p,w,\lambda ,\theta ))\text{。} \end{array} $ | (2) |
其中G为修正系数。
| $ \begin{array}{l}\textstyle G(p,w,\lambda ,\theta ) = \frac{{0.5{{(1 - {\beta ^2})}^2}\left[{\left( {1 - \frac{{{\beta ^2}}}{4}} \right)({A_{1 + }} + {A_{1 - }}) + 4{\beta ^2}{A_{1 + }}{A_{1 - }}} \right]}}{{\left( {1 - \frac{{{\beta ^2}}}{4}} \right) + {\beta ^2}\left( {1 + \frac{{{\beta ^2}}}{2} - \frac{{{\beta ^4}}}{8}} \right)({A_{1 + }} + {A_{1 - }}) + 2{\beta ^6}{A_{1 + }}{A_{1 - }}}}\\[5pt] \textstyle {A_{1 \pm }} = \frac{1}{{\sqrt {{{\left( {\frac{{p\sin \theta }}{\lambda } \pm 1} \right)}^2} - \frac{{{p^2}}}{{{\lambda ^2}}}} }} - 1 \\ \beta = \sin (0.5\pi w/p)\text{。} \end{array} $ | (3) |
需要注意的是,上述表达式适用于频率选择表面的第一栅瓣频率以下频段范围。同理,可以采用 p(1 + sinθ) < λ 的条件来判断结构旁瓣的抑制效果,其中 p 为周期单元尺寸,λ 为电磁波波长,θ 为电磁波入射角,当周期单元尺寸远小于波长时,其栅瓣抑制效果较好,上述表达式的适用频率范围也更广。
已有的研究中,频选材料结构有方环、双方环、三极型等多种周期单元[6-8],但这些频选周期单元的单元尺寸较大,性能存在诸多缺陷,如栅瓣、斜入射条件传输系数恶化等。本文针对一种新的基于多面耦合原理的小型化频率选择表面周期单元,周期约为波长的数十分之一,相对应地设计其等效电路模型。
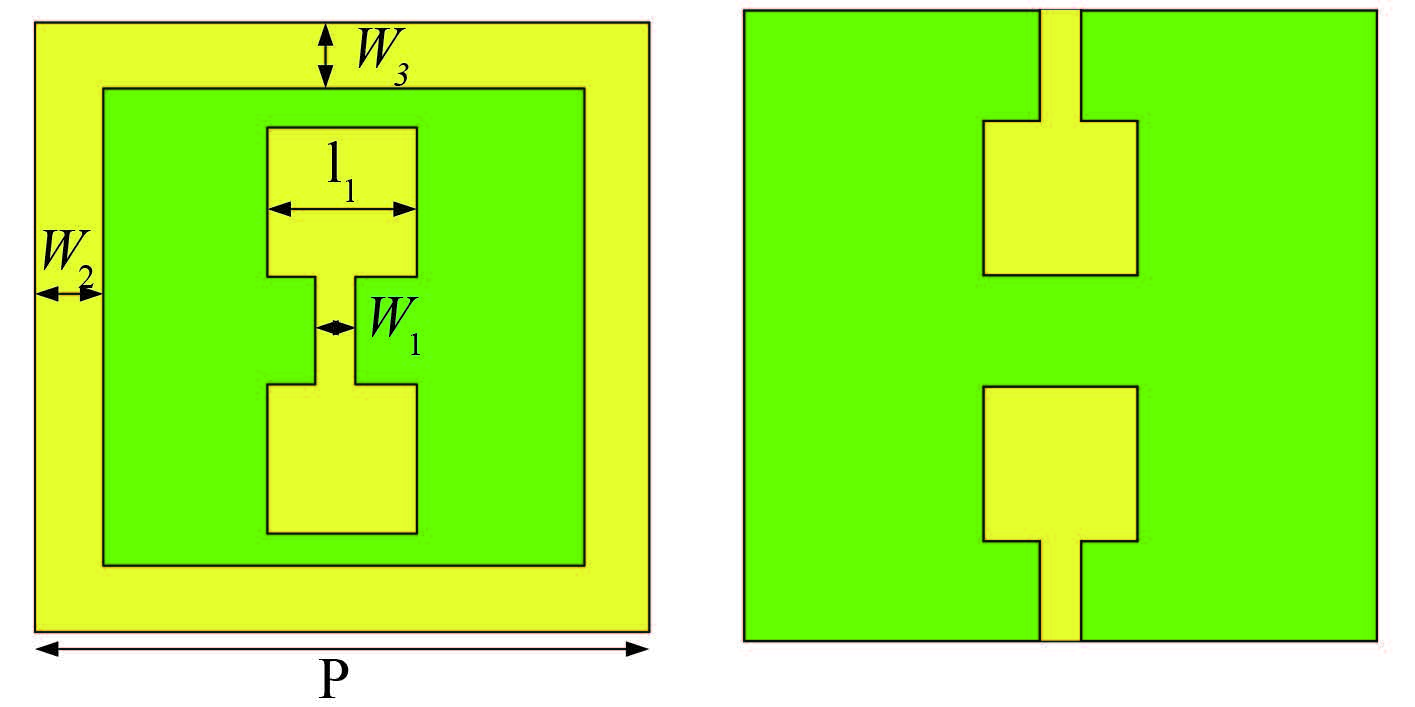
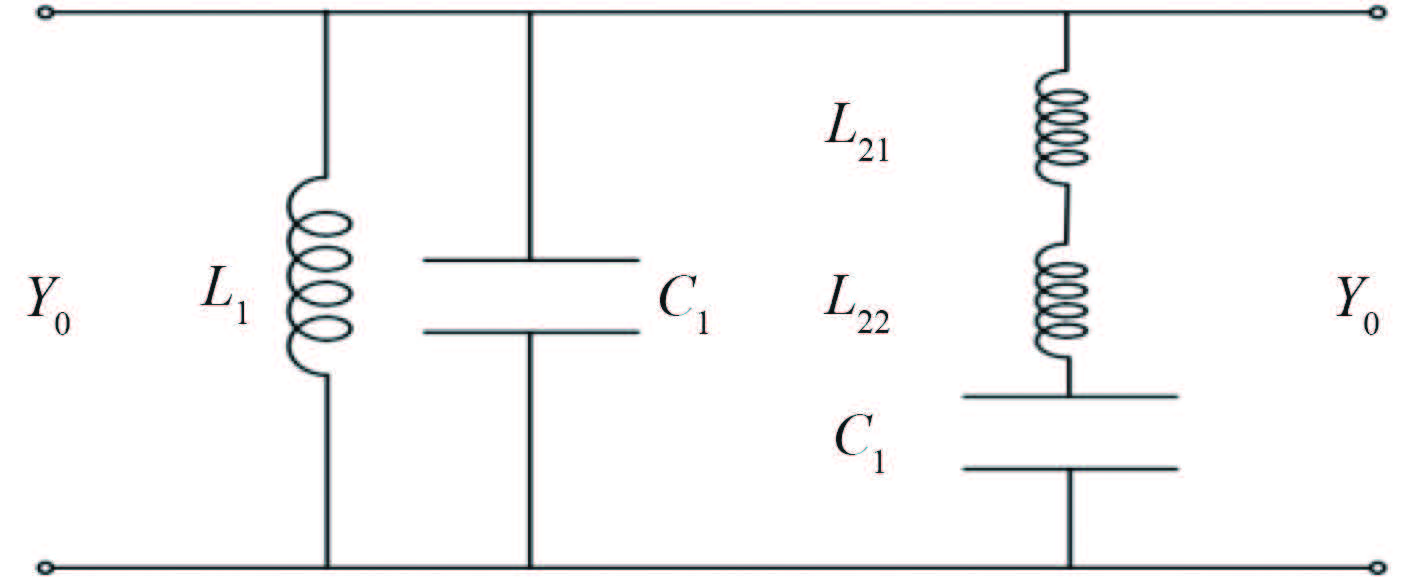
2 小型化周期单元的等效模型基于多面互耦合原理的小单元频选周期单元如图 2 所示。首先对该结构进行分解,顶层金属贴片可等效为电感 L1,贴片缝隙可等效为电容 C1,上下层贴片间耦合、顶层贴片与四周金属框之间的耦合可等效为 C2,L12,L22 构成的谐振支路。单元结构的等效模型如图 3所示,从图中可看出,该小型化周期单元能够分解成 5 个集总参数元件的并联谐振回路。
|
图 2 一种基于多面互耦合原理的小型化频率选择表面周期单元结构 Fig. 2 Miniaturization frequency selective surface cycle unit structure based on the principle of polyhedral mutual coupling |
|
图 3 小型化周期单元的传输线等效模型 Fig. 3 The equivalent transmission line model of miniaturization cycle unit structure |
再利用式(4)和式(5)计算上述各子结构的集总参数元件值,计算结果如下:
| $ \begin{array}{l} {L_1} = \displaystyle\frac{{P - 2{w_3}}}{P} \cdot \displaystyle\frac{{\lambda \cdot F\left( {P,2{w_2},\lambda } \right) \cdot {Z_0}}}{{2\pi \cdot C}}\text{,}\\ {L_{21}} = \displaystyle\frac{{P - 2{w_3} - 2{l_1}}}{P} \cdot \displaystyle\frac{{\lambda \cdot F\left( {P,{w_1},\lambda } \right) \cdot {Z_0}}}{{2\pi \cdot C}}\text{,}\\ {L_{22}} = \displaystyle\frac{{2{l_1}}}{P} \cdot \displaystyle\frac{{\lambda \cdot F\left( {P,{l_1},\lambda } \right) \cdot {Z_0}}}{{2\pi \cdot C}}\text{,}\\ {C_1} = \displaystyle\frac{{P - 2{w_2}}}{{2P}} \cdot \displaystyle\frac{{\lambda \cdot F\left( {P,P - 2{w_3},\lambda } \right)}}{{2\pi \cdot C \cdot {Z_0}}}\text{,}\\ {C_2} = \displaystyle\frac{{l_1^2 \cdot {\varepsilon _0} \cdot {\varepsilon _r}}}{{2 \cdot h}}\text{。} \end{array} $ | (4) |
其中,
| $ F(P,{D_1},\lambda) = \frac{P}{\lambda } \cdot \cos d(\theta) \cdot (\text{log}\left( {\frac{1}{{\sin \left( {\frac{{\pi \cdot D}}{{2P}}} \right)}}} \right) + G)\text{。} $ | (5) |
计算可知,频率选择表面谐振频率为:
| $ \textstyle {f_0} = \frac{{\sqrt {(({L_1} \cdot {C_2} + {L_2} \cdot {C_2} + {L_1} \cdot {C_1} - \sqrt {C_2^2 \cdot {{\left( {{L_1} + {L_2}} \right)}^2} + L_1^2 \cdot C_1^2 + 2{C_1}{C_2}{L_1}\left( {{L_1} - {L_2}} \right)} } }}{{2{C_1}{C_2}{L_1}{L_2}}}\text{。} $ | (6) |
保持整个单元尺寸以及其他结构尺寸不变的前提下,同时改变 W2 和 W3 宽度,使其分别为 0.1 mm,0.2 mm,0.4 mm,0.5 mm,0.8 mm,1.6 mm,分别利用 HFSS 仿真软件以及前述等效模型对频率选择表面的谐振频率进行仿真。由图 4 可知,两者计算结果的较为一致。

|
图 4 W2 和 W3 变化时,全波仿真及等效电路模型计算结果对比 Fig. 4 Result of simulation and equivalent circuit model while the W2 and W3 is variable |
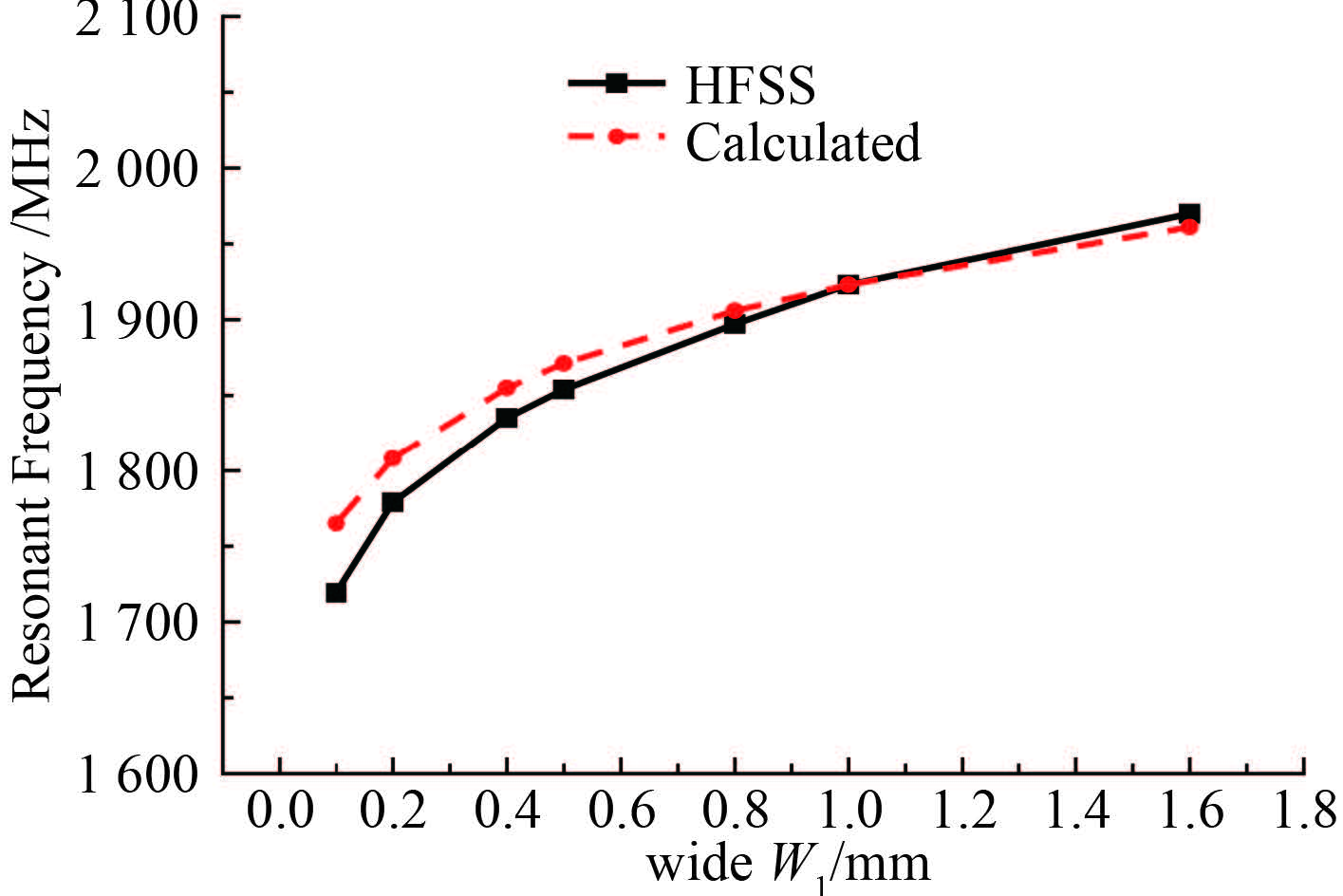
图 5 给出的是单独改变 W1,保持其他参数不变时,计算和仿真结果的对比,从图中可以看出,当 W1 较大时,计算与仿真结果还能够较好吻合,随着 W1 的减小,两者的差异逐渐明显,可见上述等效电路模型对于过细的线型结构电感值的计算略有误差。且谐振频率随 W1 的变化呈现较强非线性特性,在 W1 较小时尤为明显。
|
图 5 W1变化时,全波仿真及等效电路模型计算结果对比 Fig. 5 Result of simulation and equivalent circuit model while the W1 is variable |
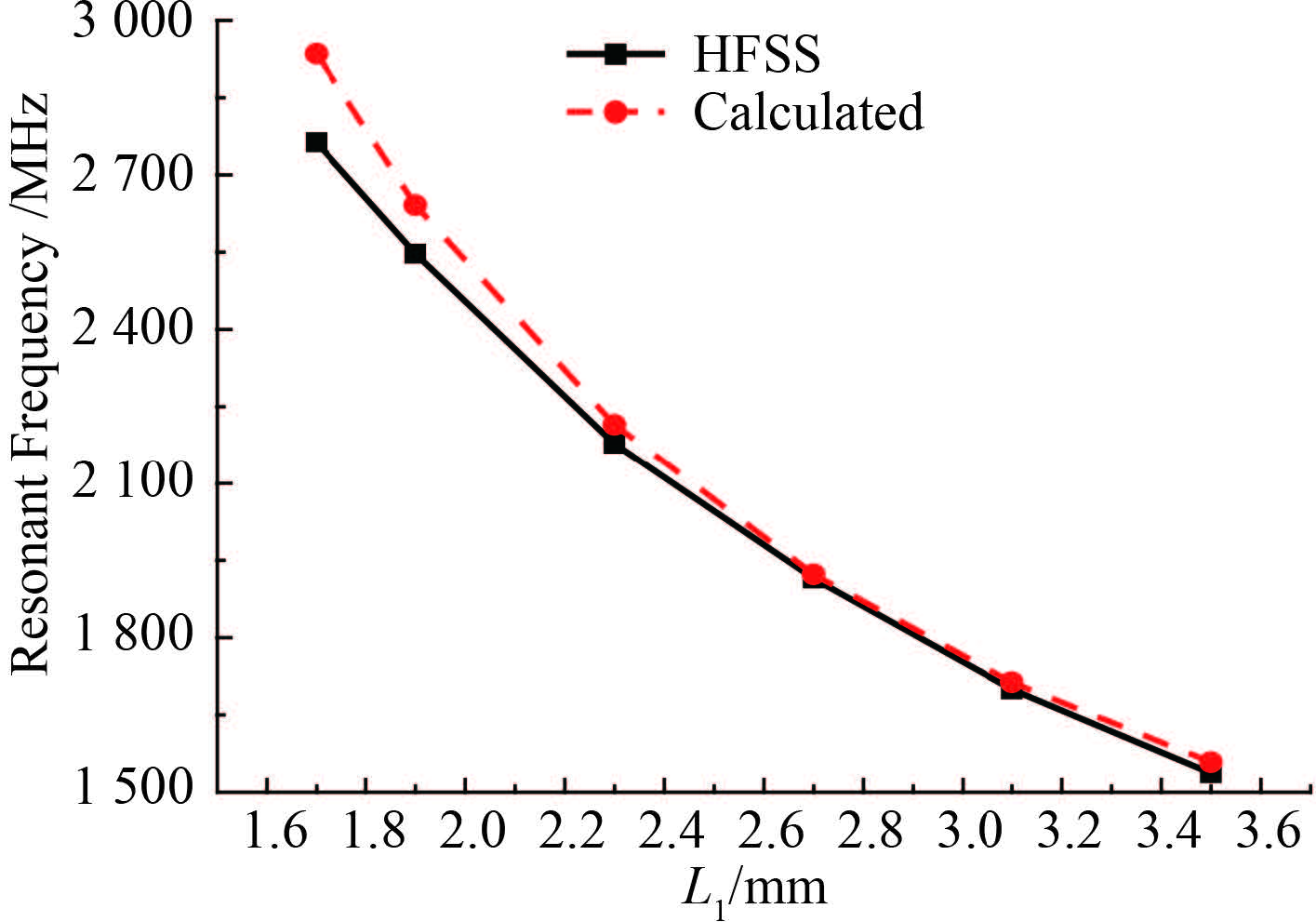
图 6 给出的是仅改变 L1 的大小,保持整个单元结构其他参数不变时的对比结果。可见,计算与仿真结果也能够较好吻合,且频率选择表面的谐振频率随着 L1 的变化快速变化。当 L1 从 1.6 mm 变为 3.5 mm 时,频选结构的谐振频率从 3 GHz 下降为 1.5 GHz。
|
图 6 L1变化时,全波仿真及等效电路模型计算结果对比 Fig. 6 Result of simulation and equivalent circuit model while the L1 is variable |
本文给出了一种小单元频率选择表面的传输线等效模型,研究发现该传输线等效模型能够较准确地对频率选择表面的谐振频率进行计算。通过该模型建立结构与模型的参数化关联,可以准确判断频选表面各尺寸参数对整个频选传输特性的影响规律,进而为频选材料的结构设计提供手段。
| [1] | MUNK B A. Frequency selective surfaces-theory and design[M]. New York: John Wiley and Sons Inc, 2000 . |
| [2] | MITTRA R, CHAN C H, CWIK T. Techniques for analyzing frequency selective surfaces-a review[J]. Proceedings of the IEEE , 1988, 76 (12) :1593–1615. DOI:10.1109/5.16352 |
| [3] | BARDI I, REMSKI R, PERRY D, et al. Plane wave scattering from frequency-selective surfaces by the finite-element method[J]. IEEE Transactions on Magnetics , 2002, 38 (2) :641–644. DOI:10.1109/20.996167 |
| [4] | LANGLEY R J, PARKER E A. Equivalent circuit model for arrays of square loops[J]. Electronics Letters , 1982, 18 (7) :294–296. DOI:10.1049/el:19820201 |
| [5] | LEE C K, LANGLEY R J. Equivalent-circuit models for frequency-selective surfaces at oblique angles of incidence[J]. IEEE Proceedings H-microwaves, Antennas and Propagation , 1985, 132 (6) :395–399. DOI:10.1049/ip-h-2.1985.0070 |
| [6] | LI Z, PAPALAMBROS P Y, VOLAKIS J L. Frequency selective surface design by integrating optimisation algorithms with fast full wave numerical methods[J]. IEE Proceedings-microwaves, Antennas and Propagation , 2002, 149 (3) :175–180. DOI:10.1049/ip-map:20020357 |
| [7] | RAHMAT-SAMⅡ Y, MICHIELSSEN E. Electromagnetic optimization by genetic algorithms:wiley series in microwave and optical engineering[M]. Hoboken, NJ, USA: Wiley-Interscience, 1999 . |
| [8] | MARCUWITZ N. Waveguide handbook[M]. New York: McGraw-Hill, 1951 . |
 2016, Vol. 38
2016, Vol. 38
