工程实际应用中,高精度导航系统需要精准的时空和方向基准作保证,进而对寻北装置的寻北精度和快速性指标提出了越来越高的要求[1-3]。捷联式惯性导航系统(SINS)以其快速启动和不可或缺的“自主性”优势,已在空天和航海等领域中广泛使用[2-6]。
捷联惯性导航系统常采用 Kalman 滤波方法进行寻北,因此,分析寻北 Kalman 滤波器的运行机制以及 SINS 和系统运行环境中噪声信号特性对滤波器运行的作用机理,得到关于滤波模型各状态的全面信息是必要的,能够为改进寻北方案和误差模型提供重要依据[4-7]。目前,已经有许多研究人员对 Kalman 滤波器的运行机制进行了深入研究[5-6],而由于噪声信号特性随不同应用具有特殊性,往往需要开展针对性研究。
文献 [8-11] 指出,SINS 测量输出信号中,随机游走噪声是影响其寻北精度的主要因素,使其成为缩短寻北时间的主要约束量。文献 [8] 得出,在导弹方位自瞄准中,降低角随机游走噪声系数或延长系统自瞄准时间可以有效提高自瞄准精度。文献 [12] 根据实验测试得出恒速偏频激光陀螺寻北仪的寻北精度与激光陀螺的角随机游走噪声系数成正比,和总寻北时间的平方根成反比。系统运行环境中噪声信号对 Kalman 滤波运行的作用主要体现为观测噪声[13-14]。文献 [15] 研究了观测噪声对 Kalman 滤波估计精度的影响。
根据可查阅的公开文献,随机游走噪声对系统寻北性能影响的结论,大都依据噪声特性[8]或重复实验测试[12]给出,尚未有从其在寻北 Kalman 滤波器中传播机理角度进行分析的研究成果发表;文献 [15] 仅通过人工离散取值对观测噪声的选取进行优化。
为更全面地分析噪声信号的影响,本文提出一种基于随机理论计算得到噪声特性与寻北 Kalman 滤波器估计差协方差矩阵之间解析式的方法,进而提取误差协方差矩阵对角线元素以表示滤波状态误差方差的滤波估计值与噪声信号系数的解析关系,即可对噪声信号对系统寻北精度和快速性的影响进行分析。该方法的独特优点是仅需要 Kalman 滤波器模型,利于在 Kalman 滤波器工程实现前进行预先理论分析和优化所设计的滤波模型[16-18]。然后,根据所采用的基于随机理论的方法,利用旋转式寻北系统进行寻北精度和快速性的详细计算,验证所采用方法的有效性。
1 基于随机理论的解析分析方法为直观地描述所关心 SINS 寻北滤波状态的估计收敛特性,得到寻北误差和相关变量之间的解析式是最有效的解决方案。考虑到误差协方差矩阵真正反映了寻北滤波状态的精度和快速性的量化值,利用误差协方差矩阵的分析方法可以直观地对寻北滤波状态的这 2 项指标进行分析[16-19]。
1.1 误差协方差矩阵的解析式连续系统 Kalman 滤波的矩阵 Riccati 方程表示为[18]:
| $ {\bf{\dot {P}}} = {FP} + {P}{{F}^{\text{T}}} + {GQ}{{G}^{\rm T}} - {P}{{H}^{\rm T}}{{R}^{ - 1}}{HP} $ | (1) |
式(1)是误差协方差矩阵 P 的非线性方程;对于高阶线性系统,一般难以通过求解上述矩阵 Riccati 方程得到 P 的显式解析式。然而,在观测噪声 R 与系统噪声 Q 不相关的假设下,可以单独分析二者对系统寻北精度和快速性的影响。利用导航计算机实际工程实现的寻北 Kalman 滤波器为离散形式,令采样计算周期为 ts,下面分别给出二者单独作用下 P 的解析式。
在无观测修正,不考虑 Kalman 滤波器的初始参数条件下,有离散化随机可控制性(Stochastic Controllablity,SC)方程[18]:
| $ \begin{array}{l} {{\bf{P}}_{SC}}\left( {k{t_s}} \right) = \\ [10pt] \displaystyle\sum\limits_{i = 0}^{k - 1} {{{\varPhi }}\left( {k{t_s},i{t_s}} \right){G}\left( {i{t_s}} \right){Q}\left( {i{t_s}} \right){{G}^{\text{T}}}\left( {i{t_s}} \right){{{\varPhi }}^{\rm T}}\left( {k{t_s},i{t_s}} \right)} \text{。} \end{array} $ | (2) |
式中:Φ(t,τ)为系统矩阵 F 的状态转移矩阵;该式表示系统噪声激励所引入的误差。
在无系统噪声和初始参数完全未知条件下,离散化随机可观测性(Stochastic Observablity,SO)方程[18]:
| $ \begin{array}{l} {{P}_{SO}}\left( {k{t_s}} \right) = \\ [6pt] \displaystyle\sum\limits_{i = 0}^k {{{{\varPhi }}^{\rm T}}\!\!\left( {i{t_s},k{t_s}} \right){{H}^{\text{T}}}\!\!\left( {i{t_s}} \right){{R}^{ - 1}}\left( {i{t_s}} \right){H}\left( {i{t_s}} \right){{\varPhi }}\left( {i{t_s},k{t_s}} \right)} \text{。} \end{array} $ | (3) |
该式表示由观测修正带来的误差抑制作用。
建立 Kalman 滤波模型后,若已知观测噪声 R 与系统噪声 Q 的统计特性,即可根据式(2)和式(3)获取噪声信号激励下的误差协方差矩阵 P 的解析表达式。
1.2 寻北 Kalman 滤波模型的建立本文以文献 [20] 中采用的单轴旋转式寻北系统为验证平台,选取姿态误差 ${\varphi ^n} = {\left[{\begin{array}{*{20}{c}} {{\phi _N}} & {{\phi _E}} & {{\phi _D}} \end{array}} \right]^{\text{T}}}$,北向速度误差 δvN,东向速度误差 δvE,b 系下陀螺零偏 ${\bf{\varepsilon }}_g^b$、b 系下 x 轴加速度计零偏 $\nabla _{ax}^b$ 和 b 系下 y 轴加速度计零偏 $\nabla _{ay}^b$ 作为估计状态,则系统状态向量为:
| $ {\bf{X}} = {\left[{\begin{array}{*{20}{c}} {{\phi _N}} \!\!\! & \!\!\! {{\phi _E}} \!\!\! & \!\!\! {{\phi _D}} \!\!\! & \!\!\! {\delta {v_N}} \!\!\! & \!\!\! {\delta {v_E}} \! & \! {\varepsilon _{gx}^b} \!\!\! & \!\!\! {\varepsilon _{gy}^b} \!\!\! & \!\!\! {\varepsilon _{gz}^b} \!\!\! & \!\!\! {\nabla _{ax}^b} \! & \! {\nabla _{ay}^b} \end{array}} \right]^{\text{T}}} \text{。} $ | (4) |
根据文献 [14] 可建立以下导航系下 φ 形式静基座寻北 Kalman 滤波器系统模型:
| $ {\bf{\dot {X}}}\left( t \right) = {F}\left( t \right){X}\left( t \right) + {G}\left( t \right){u}\left( t \right),{u}\left( t \right) \sim N\left( {0,{Q}} \right) $ | (5) |
其中:状态矩阵 F(t),系统噪声传播矩阵 G(t)详见文献 [20],且 Q 可写成:
| $ {Q} = \left[{\begin{array}{*{20}{c}} {n_{grw}^2{I_{3 \times 3}}} & {{0_{3 \times 2}}} & {{0_{3 \times 3}}} & {{0_{3 \times 2}}}\\ [6pt] {{0_{2 \times 3}}} & {n_a^2{I_{2 \times 2}}} & {{0_{2 \times 3}}} & {{0_{2 \times 2}}}\\ [6pt] {{0_{3 \times 3}}} & {{0_{3 \times 2}}} & {n_{gbrw}^2{I_{3 \times 3}}} & {{0_{3 \times 2}}}\\ [6pt] {{0_{2 \times 3}}} & {{0_{2 \times 2}}} & {{0_{2 \times 3}}} & {n_{abrw}^2{I_{2 \times 2}}} \end{array}} \right] \text{。} $ | (6) |
式中:ngrw 和 ngbrw 分别为陀螺测量输出中角随机游走噪声系数和角速率随机游走噪声系数;na 和 nabrw 分别为加速度计测量输出中相应的随机游走噪声系数。
静基座寻北 Kalman 滤波器观测量确定为北向速度误差和东向速度误差,则观测模型写成:
| $ {z}\left( t \right) = \left[{\begin{array}{*{20}{c}} {\delta {v_N}}\\ [6pt] {\delta {v_E}} \end{array}} \right] = {H}\left( t \right){X}\left( t \right){\bf{ + \upsilon }}\left( t \right), {\bf{\upsilon }}\left( t \right) \sim N\left( {0,{R}} \right) \text{。} $ | (7) |
在北向和东向速度观测噪声系数相等假设下,R 可表示为:
| $ {R} = \left[{\begin{array}{*{20}{c}} {r_v^2} & 0\\ [10pt] 0 & {r_v^2} \end{array}} \right] \text{。} $ | (8) |
结合文献 [16-17] 所采用分析方法的思路,利用其具有直观线性代数特性、不需要单调繁重的仿真实验的优点,随机可控制性和随机可观测性方程正是连接误差协方差矩阵分析和所设计寻北 Kalman 滤波模型各状态的收敛精度和快速性的有效途径。
从寻北 Kalman 滤波实际实现的角度,以下 2 点需要考虑:
1)在 IMU 器件的零偏可观情况下,一般寻北 Kalman 滤波模型均将零偏状态进行扩展,则不可避免地增加滤波模型的维数,意味着本文所研究的滤波模型是一个高阶线性系统。当寻北过程中 IMU 位置保持固定时,系统矩阵 F(t)是常值;然而,当寻北过程中改变 IMU 位置以改善系统滤波状态的可观测度时,系统矩阵是时变的,导致基于随机理论进行误差协方差矩阵分析时,计算量非常大;
2)基于随机理论的误差协方差矩阵分析方法在 SINS 对准中的成功应用成果仅有文献 [16-17](为得到解析表达式使用了简化的三维或四维模型,降低了解析式的准确度)。
因此,如何将随机理论扩展应用到高阶线性时变系统成为亟待解决的问题。
2 实验结果及分析为验证所提出的基于随机理论的解析分析方法的有效性,利用 1.2 节中给出的验证模型进行计算。本文中符号运算均采用 Mathematica 7.0 软件来实现。
方位角误差 φD 的估计精度是寻北系统应用中一个非常关键的状态参数,误差协方差矩阵 P 的第 3 个对角线元素 P(3,3)(t)可以用来表示其估计误差方差[16-17]。
2.1 系统噪声影响分析下面分析在不同转动条件下,随机游走噪声对寻北系统性能的影响。为了区分,以 P 的上标表示寻北系统采用的不同旋转方案,则 P0 表示转台转速为 0,而 P1 表示转台恒速转动。不失一般性,假定寻北系统中 ${{C}}_{{b_0}}^n = {{{I}}_{3 \times 3}}$。
根据式(2)进行计算,令 ${\Delta _1} = {\omega _{ie}}\cos L$,${\Delta _2} = \omega _{ie}^2\sin \left( {2L} \right)$,${\Delta _3} = {\omega _{ie}}\sin L$,t = kts,忽略小量的高阶乘积,有
| $ \begin{aligned} P_{\left( {3,3} \right)}^0\left( t \right) = & n_{grw}^2\left( {t + \frac{1}{3}{\Delta _1}^2{t^3} + \frac{1}{{80}}{\Delta _2}^2{t^5}} \right)+ \\ & n_{gbrw}^2\left( {\frac{1}{3}{t^3} + \displaystyle\frac{1}{{20}}{\Delta _1}^2{t^5} + \frac{1}{{1008}}{\Delta _2}^2{t^7}} \right) \text{,} \end{aligned} $ | (9) |
| $ P_{\left( {3,3} \right)}^1\left( t \right) \!=\! n_{grw}^2\left( {t + \frac{1}{3}{\Delta _1}{t^3} \!+\! \frac{1}{{80}}{\Delta _2}^2{t^5}} \right)\\ \!+\! \frac{{n_{gbrw}^2}}{{480\varOmega _C^7}}\left( \begin{array}{l} 160\varOmega _C^7{t^3} \!+\! 80\omega _{ie}^2\varOmega _C^3\left( {6 \!+\! \varOmega _C^2{t^2}} \right)t \!+\! 6{\Delta _2}^2\varOmega _C^{}\left( {40 \!+\! \varOmega _C^4{t^4}} \right)t\\ \!+\! \omega _{ie}^2\left( \begin{array}{l} 80\varOmega _C^{}\cos \left( {2L} \right)t\left( \begin{array}{l} 6\varOmega _C^2 \!+\! \varOmega _C^4{t^4}\\ \!-\! 12{\Delta _1}^2\cos \left( {\varOmega _C^{}t} \right) \end{array} \right)\\ \!+\! 160{\cos ^2}L\sin \left( {\varOmega _C^{}t} \right)\left( \begin{array}{l} \varOmega _C^2{\Delta _3}\left( {12 \!+\! \varOmega _C^2{t^2}} \right)t\\ \!+\! 6\cos \left( {\varOmega _C^{}t} \right)\left( \begin{array}{l} \varOmega _C^3 \!+\! \omega _{ie}^2\varOmega _C^{}\\ \!+\! 3{\Delta _3}\varOmega _C^2 \end{array} \right)t\\ \!+\! 3\left( {\varOmega _C^{} \!+\! {\Delta _3}} \right)\left( \begin{array}{l} \!-\! 4\varOmega _C^{} \!-\! 6{\Delta _3}\\ \!+\! \varOmega _C^2{t^2}{\Delta _3} \end{array} \right) \end{array} \right) \end{array} \right) \end{array} \right) \text{。} $ | (10) |
式中:ΩC 为转台转速;ωie 为地球自转角速率;L 为当地地理纬度。
根据上述 2 式,可明显看出:随机游走噪声是方位角误差 φD 估计精度的主要影响因素。
比较不同转台旋转方案下陀螺随机游走噪声对方位角误差 φD 影响随时间的变化,可得出以下结论:
1)旋转调制对陀螺角随机游走噪声对方位角误差的影响没有抑制效果;
2)旋转调制对角速率随机游走噪声对方位角误差的影响有抑制效果。
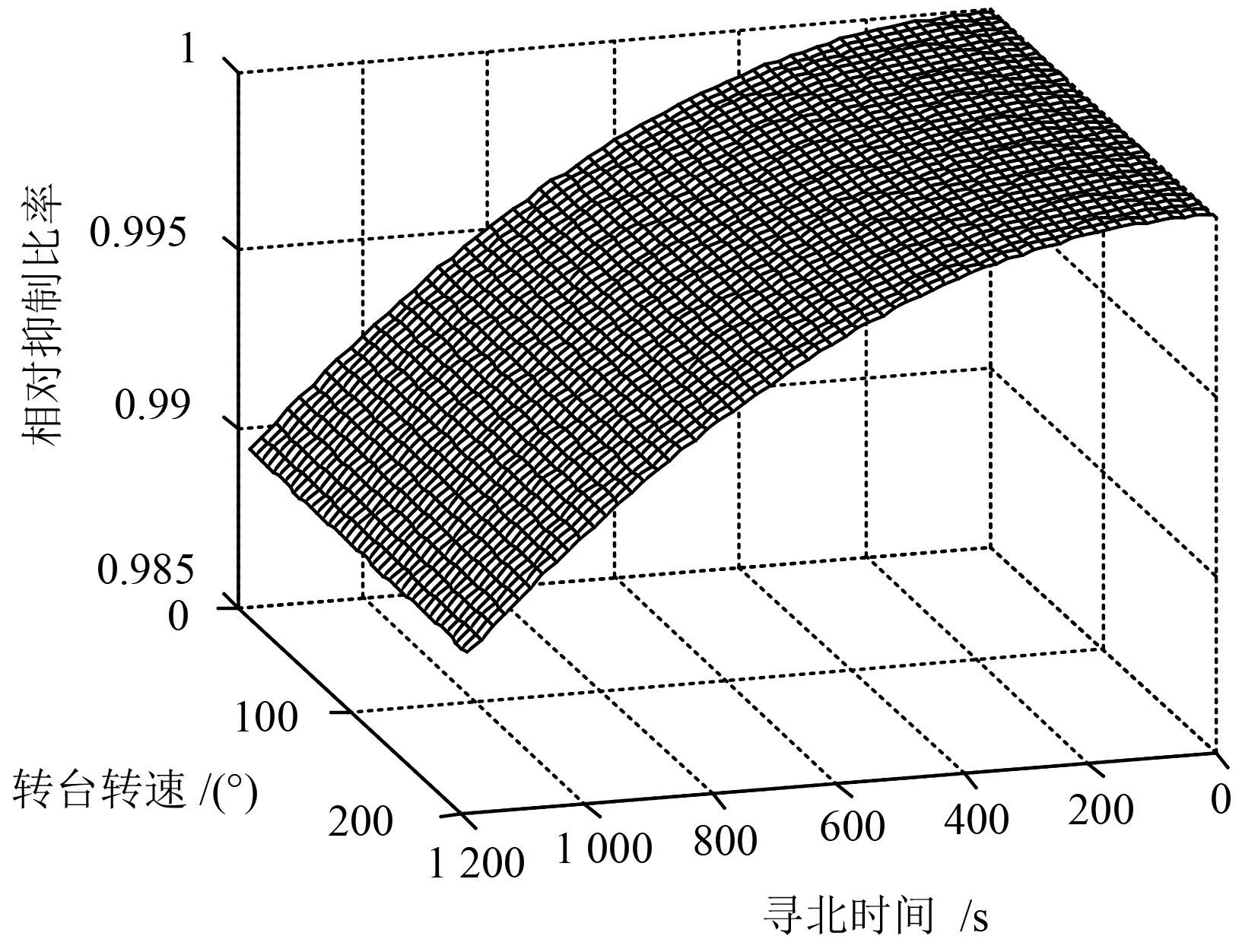
为更直观地观察旋转调制对角速率随机游走噪声对方位角误差影响的抑制效果,图 1 给出了转台转动情况下陀螺角速率随机游走噪声对方位角误差作用分量与转台转速为 0 时其作用分量的比值。
|
图 1 旋转调制对陀螺角速率随机游走噪声对方位角误差作用分量的相对抑制比率 Fig. 1 Attenuation ratio of gyro angular rate random walk noise influence on azimuth error under different turntable rate(> 0)compared to zero turntable rate |
由图 1 可见,旋转调制对陀螺角速率随机游走噪声对方位角误差影响的抑制作用随时间变化缓慢;在寻北快速性指标的要求下,旋转调制抑制陀螺角速率随机游走噪声对方位角估计精度的提高影响较小。
上述结论与已公开的研究成果一致[13-14, 21],说明基于随机理论的解析方法的有效性,用于分析寻北系统的适用性。
2.2 观测噪声影响分析相对于系统噪声影响分析,观测噪声影响分析计算量大大增加。为简化验证计算,不失一般性,式(3)中除观测噪声系数之外的其他影响变量都将赋予一个确定数值,见表 1。
|
|
表 1 影响变量数值设定 Tab.1 Set values of the influencing variables |
根据式(3),利用表 1中参数取值,令 t = kts = 600 s,可以得到采用 1.2 节给出的验证模型时方位角误差标准差与观测噪声标准差之间关系的解析表达式为:
| $ \sqrt {P_{\left( {3,3} \right)}^{}\left( t \right)} = {\rm{0}}{\rm{.01448427}}{r_\nu } \text{。} $ |
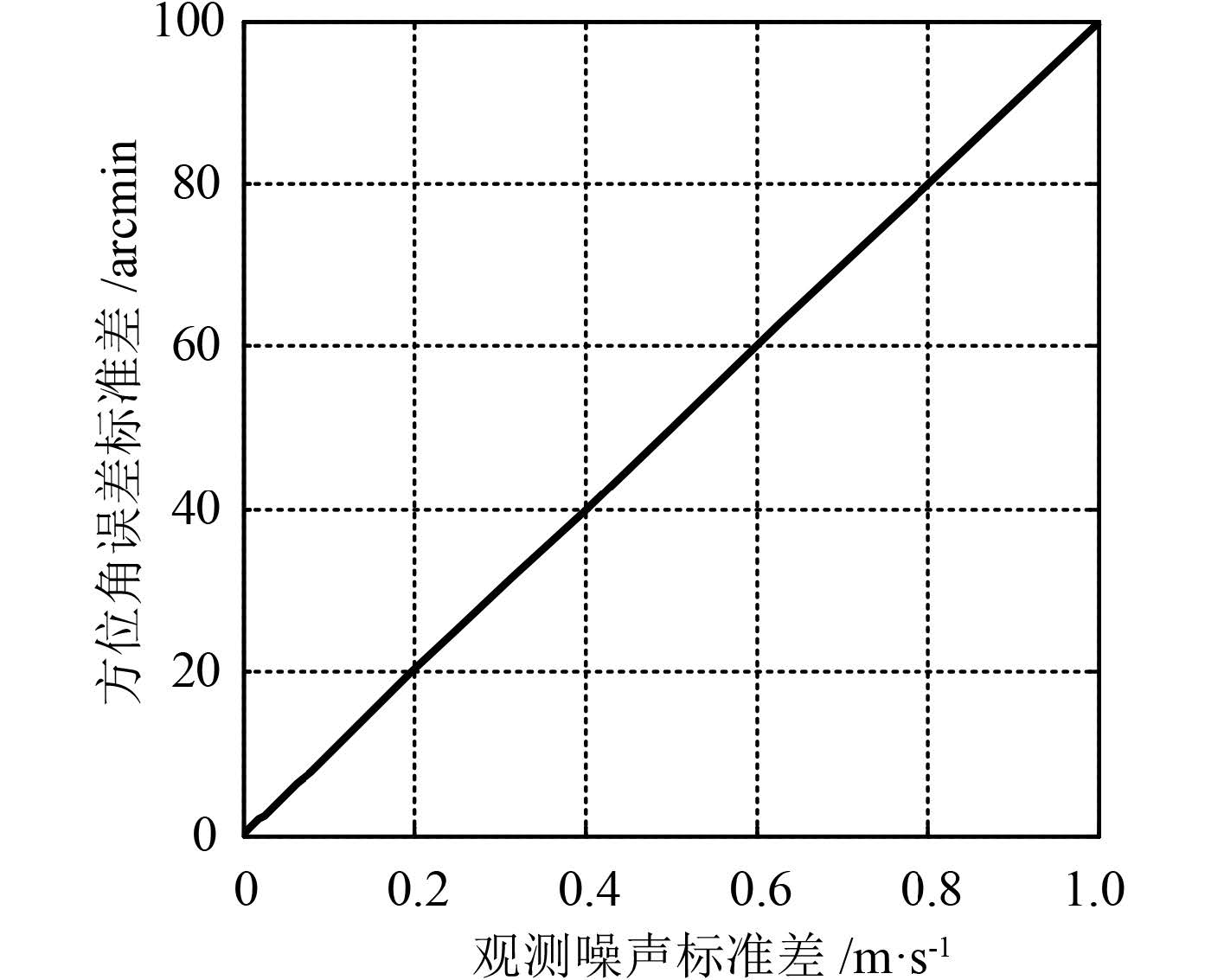
采用 1.2 节给出的验证模型寻北结束时方位角误差标准差与观测噪声标准差之间的关系曲线如图 2 所示。观测噪声标准差的取值范围为 0.000 1 ~ 1 m/s。
|
图 2 寻北结束时方位角误差标准差与观测噪声标准差之间的关系曲线 Fig. 2 Standard deviation curve between azimuth error and measurement noise after north-filtering |
由解析式(11)和图 2 可见,利用基于随机理论的解析方法能够得到所关心状态与影响变量之间的简洁解析表达式,有利于对系统性能进行深入分析。同时,根据图 2,当转台转速确定时,采用 1.2 节给出的验证模型寻北结束时方位角误差标准差与观测噪声标准差在理论上成正比。
3 结 语Kalman 滤波在捷联惯性导航系统的初始对准和标定等各个环节广泛应用。为了能够更全面地深入研究 SINS 和系统运行环境中噪声信号特性对滤波器运行的作用机理,得到关于滤波模型各状态的全面信息,本文利用随机可控制性和随机可观测性得到滤波噪声在寻北 Kalman 滤波器影响作用的解析表达式,利用单轴旋转式寻北系统对所提出的基于随机理论的解析分析方法进行了计算验证。根据详细验证结果可见,基于随机理论的解析分析方法适用于寻北系统,分析结论与已公开研究结论一致,并且利用该方法还能够得到更全面的系统性能分析结果,具有较高的理论参考价值。
| [1] | EL-OSERY A, BRUDER S, LAUGHLIN D. High-accuracy heading determination[C]//Proceedings of the 8th international Conference on System of Systems Engineering. Maui, Hawaii, USA:IEEE, 2013:308-313. |
| [2] | PESHEKHONOV V G. Gyroscopic navigation systems:current status and prospects[J]. Gyroscopy and Navigation , 2011, 2 (3) :111–118. DOI:10.1134/S2075108711030096 |
| [3] | GIBSON C, FLUECKIGER K, HOPKINS R, et al. Demonstrating practical inertial navigation:the beginnings and beyond[C]//Proceedings of AIAA Guidance, Navigation, and Control (GNC) Conference. Boston, MA:American Institute of Aeronautics and Astronautics, 2013:5122. |
| [4] | LEE M H, PARK W C, LEE K S, et al. Observability analysis techniques on inertial navigation systems[J]. Journal of System Design and Dynamics , 2012, 6 (1) :28–44. DOI:10.1299/jsdd.6.28 |
| [5] | GREWAL M S, HENDERSON V D, MIYASAKO R S. Application of kalman filtering to the calibration and alignment of inertial navigation systems[J]. IEEE Transactions on Automatic Control , 1991, 36 (1) :4–13. |
| [6] | GREWAL M S, ANDREWS A P. Applications of Kalman filtering in aerospace 1960 to the present[J]. IEEE Control Systems , 2010, 30 (3) :69–78. DOI:10.1109/MCS.2010.936465 |
| [7] | LU S L, XIE L, CHEN J B. Reduced-order Kalman filter for RLG SINS initial alignment[C]//Proceedings of 2008 Chinese Control and Decision Conference. Yantai, China:IEEE, 2008:3675-3680. |
| [8] |
杨俊峰, 司文杰. 陀螺随机游走对导弹自瞄准精度的影响[J]. 航天控制 , 2012, 30 (5) :21–24.
YANG Jun-feng, SI Wen-jie. The effect of gyro random walk during the process of initial alignment of missile[J]. Aerospace Control , 2012, 30 (5) :21–24. |
| [9] | ALBO M, BRONSHTEYN B. North finding device, system and method:US, 8151475[P]. 2012-04-10. |
| [10] | LI Z K. Gyrocompass modeling and simulation system (GMSS) and method thereof:US, 20130179134 A1[P]. 2013-07-11. |
| [11] |
高贤志. 陀螺角度随机游走误差对旋转惯导系统的影响[J]. 舰船科学技术 , 2014, 36 (9) :122–124,135.
GAO Xian-zhi. Research on the influence of rotation inertial navigation due to gyro angle random walk error[J]. Ship Science and Technology , 2014, 36 (9) :122–124,135. |
| [12] |
黄宗升, 秦石乔, 王省书, 等. 恒速偏频激光陀螺寻北仪的研究[J]. 弹箭与制导学报 , 2007, 27 (5) :65–67.
HUANG Zong-sheng, QIN Shi-qiao, WANG Xing-shu, et al. The study on north-finder based on constant rate biased RLG[J]. Journal of Projectiles, Rockets, Missiles and Guidance , 2007, 27 (5) :65–67. |
| [13] | GROVES P D. Principles of GNSS, inertial, and multisensor integrated navigation systems[M]. 2nd ed. Boston, London UK: Artech House, 2008 : 140 -153. |
| [14] | ROGERS R M. Applied mathematics in integrated navigation systems[M]. 2nd ed. Reston, VA: American Institute of Aeronautics and Astronautics, Inc, 2006 : 132 -161. |
| [15] |
程向红, 郑梅. 捷联惯导系统初始对准中Kalman参数优化方法[J]. 中国惯性技术学报 , 2006, 14 (4) :12–17.
CHENG Xiang-hong, ZHENG Mei. Optimization on Kalman filter parameters of SINS during initial alignment[J]. Journal of Chinese Inertial Technology , 2006, 14 (4) :12–17. |
| [16] | BAR-ITZHACK I Y, PORAT B. Azimuth observability enhancement during inertial navigation system in-flight alignment[J]. Journal of Guidance, Control, and Dynamics , 1980, 3 (4) :337–344. DOI:10.2514/3.55999 |
| [17] | PORAT B, BAR-ITZHACK I Y. Effect of acceleration switching during INS in-flight alignment[J]. Journal of Guidance, Control, and Dynamics , 1981, 4 (4) :385–389. DOI:10.2514/3.19744 |
| [18] | GELB A. Applied optimal estimation[M]. 16th ed. Cambridge, Massachusetts, USA: MIT Press, 2001 : 92 -154. |
| [19] |
杨晓霞, 阴玉梅. 可观测度的探讨及其在捷联惯导系统可观测性分析中的应用[J]. 中国惯性技术学报 , 2012, 20 (4) :405–409.
YANG Xiao-xia, YIN Yu-mei. Discussions on observability and its applications in SINS[J]. Journal of Chinese Inertial Technology , 2012, 20 (4) :405–409. |
| [20] | YU H P, ZHU H, GAO D Y, et al. A stationary north-finding scheme for an azimuth rotational IMU utilizing a linear state equality constraint[J]. Sensors , 2015, 15 (2) :4368–4387. DOI:10.3390/s150204368 |
| [21] | BRITTING K R. Effects of azimuth rotation on gyrocompass systems[C]//Proceedings of the 34th Annual Meeting of the Institute of Navigation. Arlington, TX, USA:ION, 1978:1-13. |
 2016, Vol. 38
2016, Vol. 38
