混响是影响主动声呐工作性能的重要干扰因素之一,混响的预报对声呐的使用和设计有着重要意义。对混响信号仿真的研究主要包括混响强度仿真[1-3]和混响时间序列仿真。当声呐系统所采用的信号处理方法主要依赖能量时,常用混响强度对其进行估计和评价。随着声呐系统的发展,如多波束和复杂相干信号处理技术的应用,就需要对混响时间序列进行仿真。混响时间序列仿真的方法主要有 2 种,一种是根据混响信号的概率分布,仿真所需分布的混响信号[4-6];另一种是以点散射模型为基础的仿真方法,即通过计算散射体或通过网格划分海底为小散射元的散射信号在接收点的叠加得到混响信号,很多文献中混响仿真方法都是以此模型为基础的改进和扩展[7-13],该方法能够比较准确地仿真混响信号,但由于海洋中存在大量散射体,在混响仿真时存在计算量大的问题。一般来说,同一时期的 GPU 其浮点运算能力和内存带宽要比 CPU 高一个数量级左右,并且显卡厂商 NVIDIA 推出的运算平台 CUDA 简单易用,使得科研工作者能够把更多的精力放在算法上,将已有算法进行简单的修改就可以得到十分可观的加速比,因此使用 GPU 并行计算非常适合科学计算。基于这个问题,采用 GPU 运算的方法则能很好地解决由计算量大引起的运算时间长的缺点,这样就能快速准确地仿真混响信号。
1 海底混响信号模型在浅海近程,由于海底的一次散射对海底混响的贡献最大,因此对海底混响信号模型的建立,也只考虑海底 1 次散射,共 4 类声线,声线如图 1 所示。
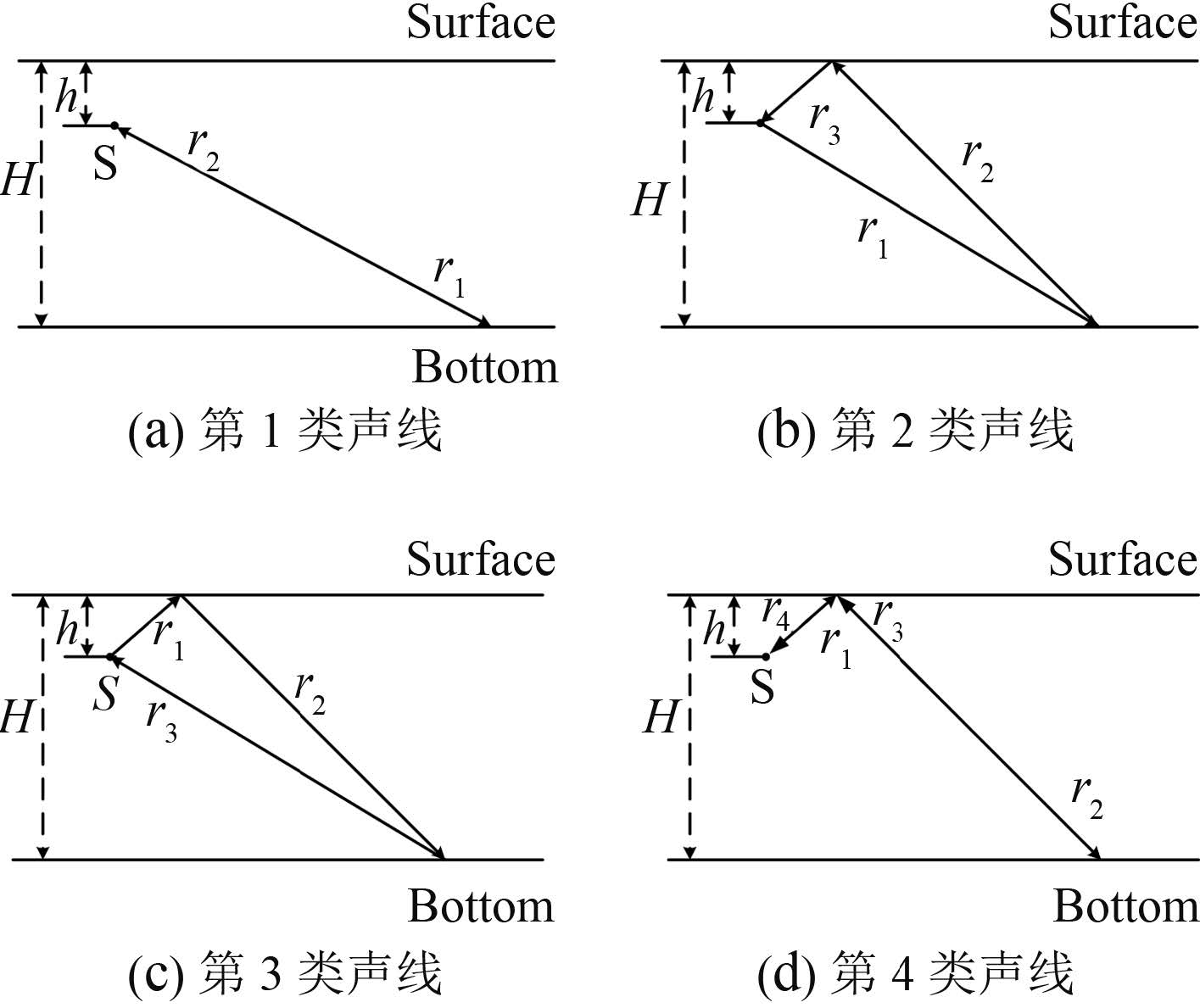
|
图 1 声线示意图 Fig. 1 Schematic plan of sound ray |
混响信号模型不考虑海面的散射;海水均匀、无吸收、恒定声速;入射声波及散射声波按球面波扩张。海底水平,海水深度为 H,声源与接收水听器合置且声源到海面的距离为 h,恒定声速为 c,海面反射系数为 m。海底散射单元的大小依据海底散射系数空间相关半径选取,海底的声压散射系数幅值和相位在此空间相关半径之内为同一数值,而在此空间相关半径之外,则为服从相同分布的其他数值。
粗糙海底散射强度由 Lambert 定律确定,声强 Ii 为入射波以掠射角 θi 入射到粗糙单位面元上,各方向上的散射声强度为:
| $ {I_s} = \mu \sin {\theta _i}\sin {\theta _s}{I_i}\text{。} $ | (1) |
式中:μ 为比例常数;θs 为散射掠射角。
由于声强与声压幅值的平方成比例,则散射声压幅值为:
| $ {P_s} = \mu {\rm{'}}\sqrt {\sin {\theta _i}\sin {\theta _s}} \cdot {P_i}\text{。} $ | (2) |
式中:μ' 为比例常数;Pi 和 Ps 分别为入射声压幅值和散射声压幅值。
根据混响的统计特性:混响的瞬时幅值为正态分布;瞬时相位为(0~2π)均匀分布,令海底声压散射系数为:
| $ {S_p} = \mu _p^{'}\sqrt {\sin {\theta _i}\sin {\theta _s}} \cdot {e^{j\phi }}\text{。} $ | (3) |
式中:μ'p 服从高斯分布 N(a,σ2)(a 为均值,σ 为方差),φ 服从(0~2π)均匀分布。
1)第 1 类声线 tk 时刻混响信号
若发射信号为脉宽为 τ 的窄带脉冲信号 s(t),tk 时刻散射声的散射区域为一同心圆环,将散射区域依据海底散射系数相关半径划分为 N1 个散射元,各散射元散射系数的幅值相互独立,且皆服从相同高斯分布,相位也相互独立并服从(0~2π)均匀分布,因此散射信号在接收点迭加后为:
| $ \begin{array}{l} {p_1}({t_k}) = \sum\limits_{l = 1}^{{N_1}} {\frac{{s(t - {t_k})}}{{{r_1}}}} {s_{{p_l}}}{\rm d}A\frac{1}{{{r_1}}} =\\ \displaystyle \frac{{s(t - {t_k})}}{{{r_1}^2}} \cdot {\rm d}A \cdot \sqrt {\sin {\theta _{{i_1}}}\sin {\theta _{{s_1}}}} \cdot \displaystyle\sum\limits_{l = 1}^{{N_1}} {\mu _{{p_l}}^{'}} {e^{j{\phi _l}}}\text{。} \end{array} $ | (4) |
由于声源与接收水听器合置,因此 sin(θi1)=sin(θs1)=(H - h)/r1,式(4)可化为:
| $ {p_1}({t_k}) = \frac{{s(t - {t_k})}}{{{r_{\rm{1}}}^{\rm{2}}}} \cdot \frac{{{{H - h}}}}{{{r_1}}}dA \cdot \sum\limits_{l = 1}^{{N_1}} {\mu _{{p_l}}^{'}} {e^{j{\phi _l}}}\text{。} $ | (5) |
2)第 2 类声线 tk 时刻混响信号
同理,tk 时刻此类声线的海底散射元为 N2,则第 2 类声线的混响信号为:
| $ \begin{array}{l} {p_2}({t_k}) \!\!=\!\! \displaystyle\frac{{m \!\cdot\! s(t - {t_k})}}{{{r_1} \!\cdot\! ({r_2} + {r_3})}} \!\cdot\! dA \!\cdot\!\! \sqrt {\sin {\theta _{{i_2}}}\sin {\theta _{{s_2}}}} \displaystyle\sum\limits_{l = 1}^{{N_2}} {\mu _{{p_l}}^{'}} {e^{j{\phi _l}}}\text{。} \end{array} $ | (6) |
式中:tk=(r1+r2+r3)/c;sin(θi2)=(H - h)/r1;其他参数同前。
3)第 3 类声线 tk 时刻混响信号
同理,tk 时刻此类声线的海底散射元为N3,则第 2 类声线的混响信号为:
| $ \begin{array}{l} {p_{\rm{3}}}({t_k}) \!\!=\!\! \displaystyle\frac{{m \cdot s(t - {t_k})}}{{{r_1} \!\cdot\! ({r_2} + {r_3})}} \!\cdot\! dA \!\cdot\!\! \sqrt {\sin {\theta _{{i_{\rm{3}}}}}\sin {\theta _{{s_{\rm{3}}}}}} \displaystyle\sum\limits_{l = 1}^{{N_{\rm{3}}}} {\mu _{{p_l}}^{'}} {e^{j{\phi _l}}}\text{。} \end{array} $ | (7) |
式中:tk=(r1+r2+r3)/c;sin(θi3)= (H+h)/(r2+r3);sin(θs3)=(H-h)/r1,其他参数同前。
4)第 4 类声线 tk 时刻混响信号
同理,tk 时刻此类声线的海底散射元为 N4,则第 2 类声线的混响信号为:
| $ \begin{array}{l} {p_{\rm{4}}}({t_k}) \!\!=\!\! \displaystyle\frac{{{m^{\rm{2}}} \!\cdot\! s(t - {t_k})}}{{{{({r_2} \!+\! {r_3})}^{\rm{2}}}}} \!\cdot\! dA \!\cdot\!\! \sqrt {\sin {\theta _{{i_{\rm{4}}}}}\sin {\theta _{{s_{\rm{4}}}}}} \displaystyle\sum\limits_{l = 1}^{{N_{\rm{4}}}} {\mu _{{p_l}}^{'}} {e^{j{\phi _l}}}\text{。} \end{array} $ | (8) |
式中:tk=2(r2+r3)/c;sin(θi4)= sin(θs4)= (H+h)/(r2+r3);其他参数同前。
将这四类声线的混响信号按时间累加即得总混响信号。
2 基于 GPU 的快速计算方法CPU 为提高分支指令的处理速度,其很多部件都用于做分支预测,以及在分支预测错误的时候修正和恢复算术逻辑单元的结果,这将大大增加器件的复杂度,使其更侧重于灵活高效的处理速度而非计算能力。相比之下,GPU 在设计之初就定位于大量数据的并行计算,发展到现在已经具有非常强大的计算能力,其核心如图 2 所示。以市面上最强桌面 CPU—Intel Core i7 5960 X 来说,它具有 8 个核心 16 个线程,默认频率 3.3 GHz,配合 AVX2 指令集其运算能力可以达到 422 Gflop/s,其内存带宽大约为 68 GB/s;而同一时期的最强桌面 GPU—GTX TITAN X 具有 3 072 个 CUDA 核心,默认频率 1 006 MHz,配合 FMA 指令集其运算能力可以达到 6 181 Gflop/s,其内存带宽大约为 336 GB/s,并且 1 台计算机中可以搭配多个 GPU,由此可见 GPU 并行计算的巨大优势。
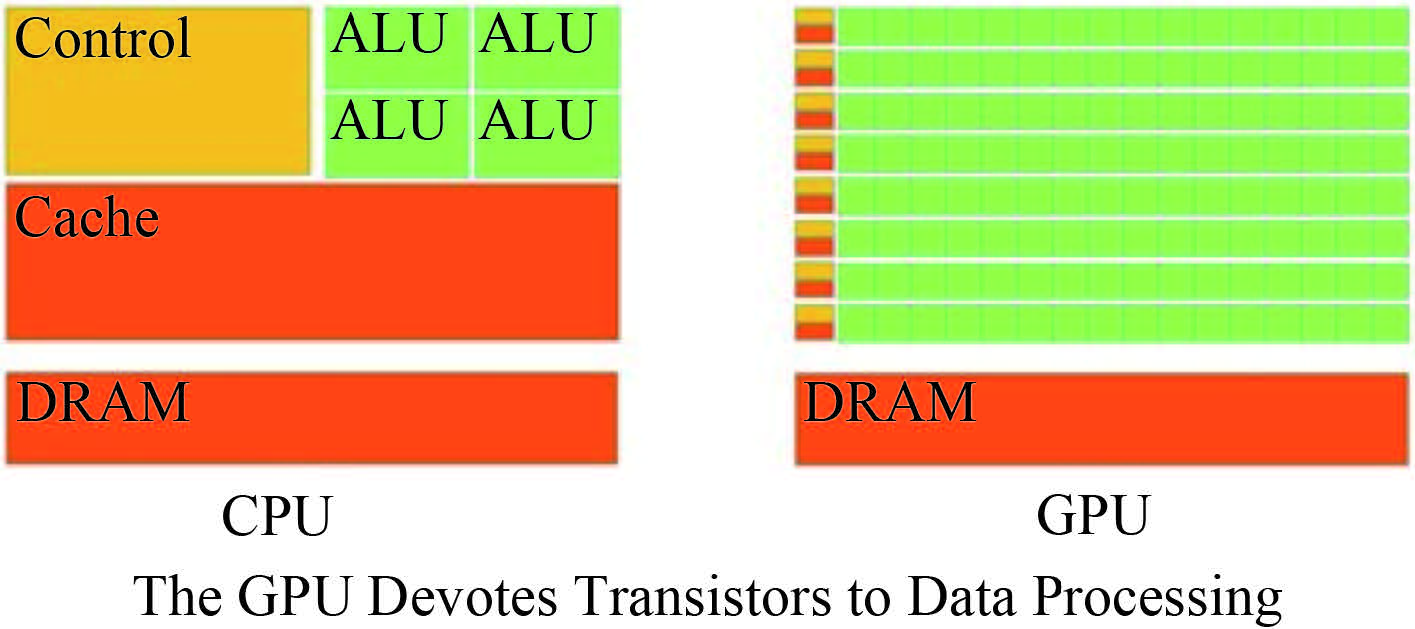
|
图 2 CPU 与 GPU 运算单元示意图 Fig. 2 Schematic plan of CPU and GPU arithmetic element |
CUDA(Compute Unified Device Architecture)是显卡厂商 NVIDIA 推出的运算平台,在 CUDA 的架构下,程序分为 host 端和 device 端 2 个部分。Host 端是指在 CPU 上执行的部分,而 device 端则是在 GPU 上执行的部分。Device 端的程序又称为“kernel”。通常 host 端程序会将数据准备好后,复制到显卡的内存中,再由显示芯片执行 device 端程序,完成后再由 host 端程序将结果从显卡的内存中取回。
基于此原理,将仿真混响信号的程序进行 GPU 编译,流程如图 3 所示。
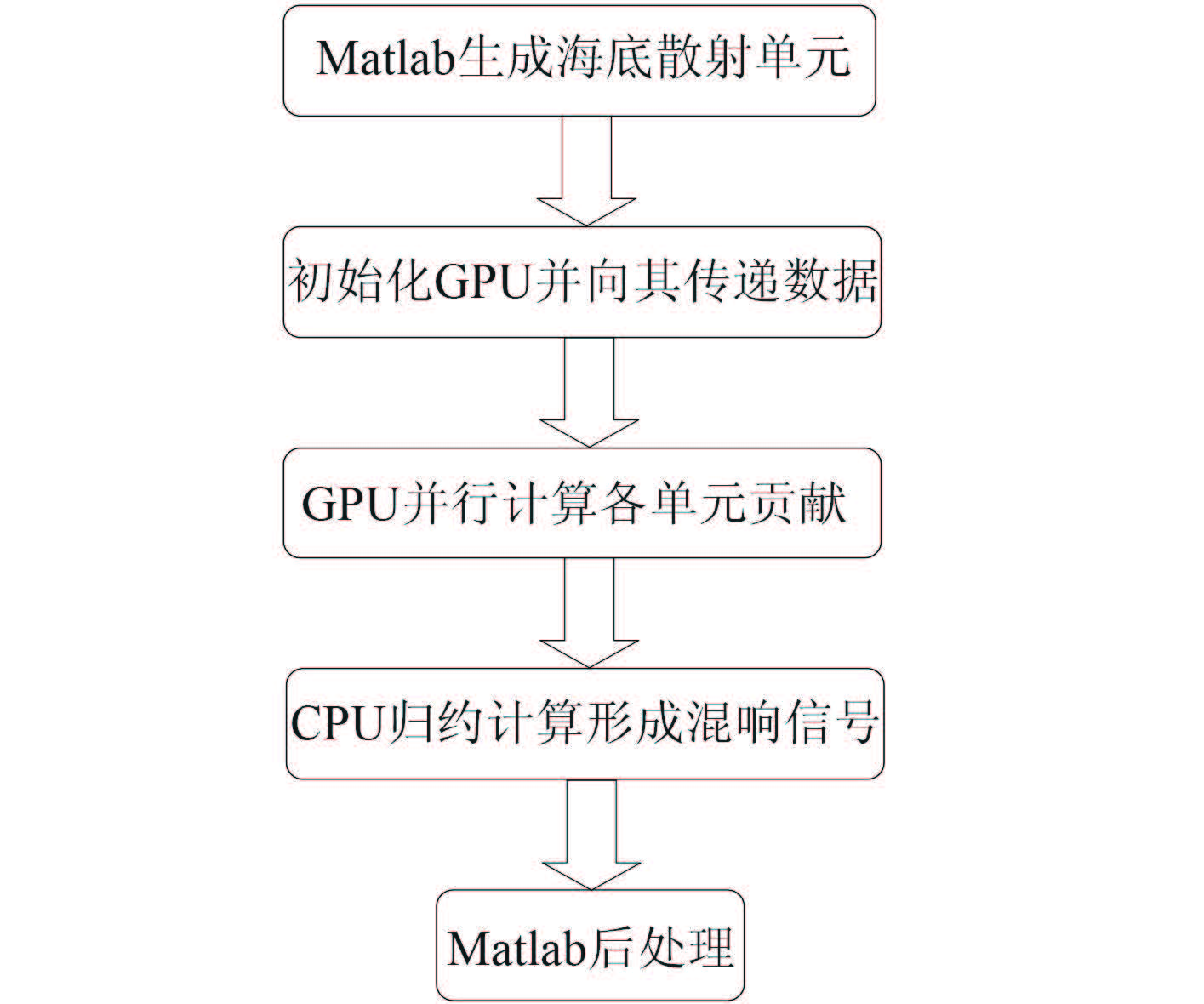
|
图 3 海底混响信号 GPU 运算流程图 Fig. 3 Flow chart of reverberation signal calculation by using GPU |
同样仿真 1.1 s 的海底混响信号,用 GPU 进行运算与用 CPU 进行运算的时间对比如表 1 所示。由表 1 可看出,运用 GPU 进行运算能极大幅度提高运算速度,减少运算时间,这为以后混响信号的实时演示验证提供一条途径。
|
|
表 1 CPU 与 GPU 运算时间对比 Tab.1 The comparison of operation time between Cpu and Gpu |
当发射信号为 20 kHz 的 CW 信号,幅值为 1 V,脉宽 τ = 5 ms,水中声速 c=1 500 ms,海深 50 m,海面反射系数 m = 0.9,收发换能器距水面 5 m 时,仿真得到如图 4 所示的混响信号波形。
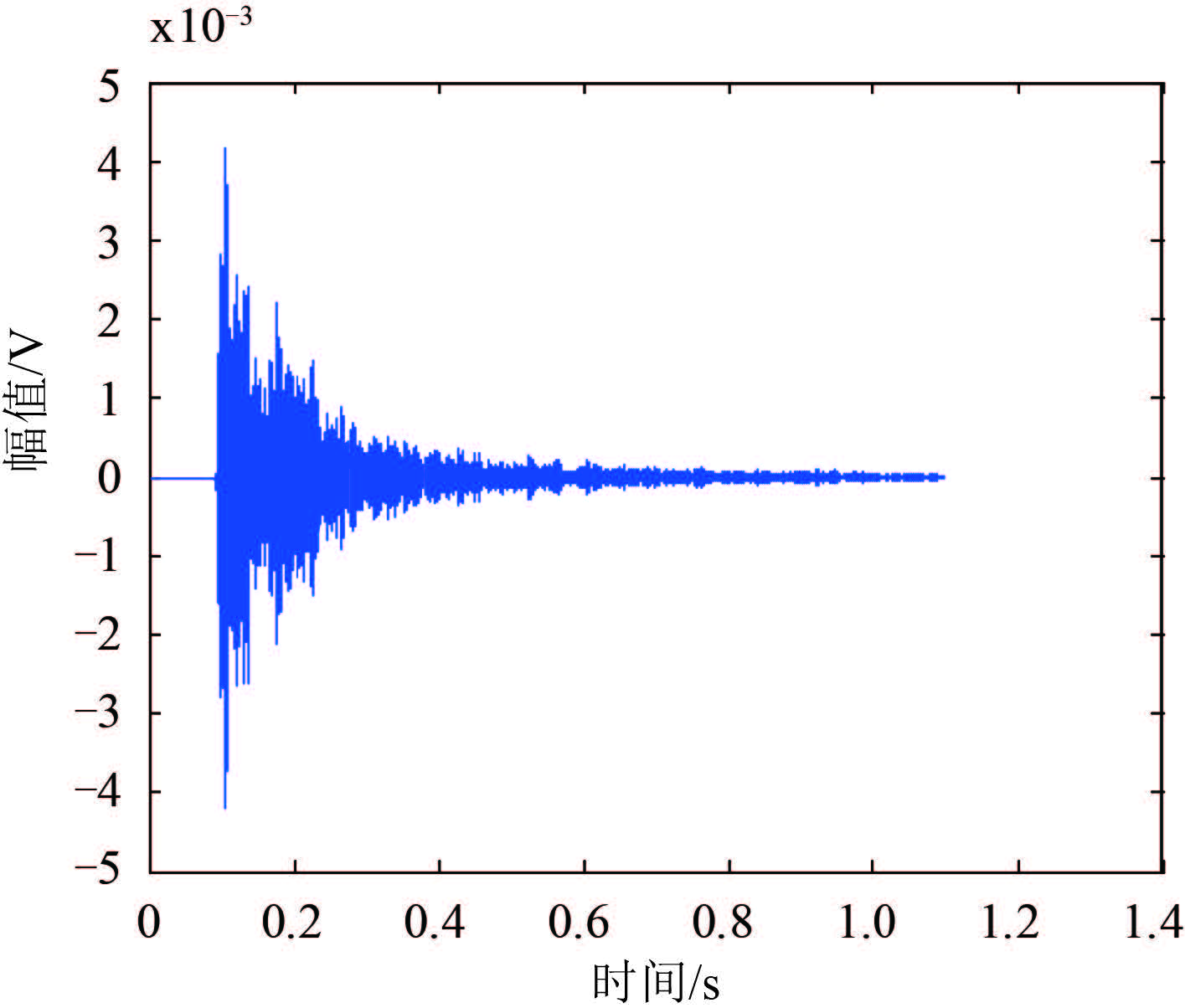
|
图 4 仿真混响信号波形图 Fig. 4 The simulation oscillogram of reverberation signal |
取 0.15 s 处的一段混响信号进行频数统计,并用直方图表示,这种直方图可以估计总体的概率密度,而为便于观察,可提取直方图高度是频率组距的情况的包络,用曲线形式近似反映样本总体的概率密度。用此方法对此段仿真信号得到的样本分布形式进行估计,并分别对用 K 分布和瑞利分布曲线拟合与仿真样本数据统计得到的结果进行比较,如图 5 所示。

|
图 5 混响信号包络统计概率 Fig. 5 The statistical probability of reverberation signal envelope |
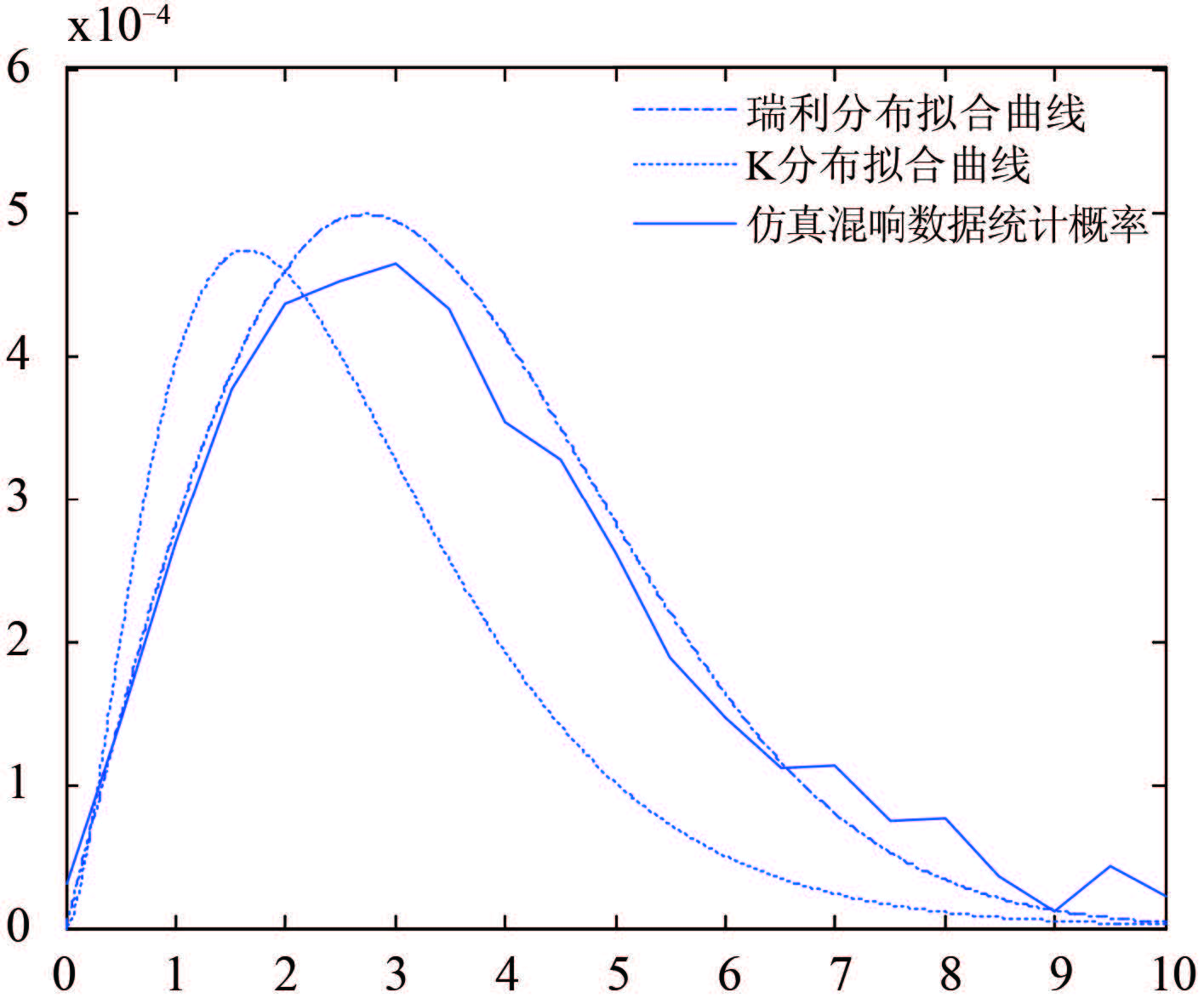
同样的方法对 0.5 s 处的一段混响信号进行处理,得到的结果如图 6 所示。
|
图 6 混响信号包络统计概率 Fig. 6 The statistical probability of reverberation signal envelope |
由图 5 可知,当在近程时,各个散射单元散射声信号叠加后形成的混响信号的包络趋于 K 分布,与传统理论中混响信号的包络呈瑞利分布不相符,这是由于传统理论中,只有当散射波的数量足够多时,其混响信号的包络才会服从瑞利分布,而在近程,散射单元的个数较少,不满足大数定理,因此会有此现象产生。而图 6 则说明在相对远程处,散射单元的个数增多,满足大数定理,则此时混响信号的包络就会趋于瑞利分布而非呈 K 分布。进而验证混响信号的合理性。
4 结 语根据混响产生的物理机理,以射线声学为基础,用 Lambert 散射定律计算海底反向散射强度,采用单元散射模型建立海底混响信号模型。通过对仿真混响信号的处理分析,在散射点较少时,混响信号包络更接近于 K 分布,而随着散射点的增多,混响信号的包络接近于瑞利分布,符合混响信号的一般统计特性,验证了混响信号模型的合理性。由于 GPU 相比于 CPU 具有更高的浮点运算能力和内存带宽,因此采用 GPU 进行计算,能快速仿真出混响信号,达到高效的目的,为今后混响信号的实时演示验证提供一条可供选择的途径。
| [1] | 姚万军, 蔡志明. 浅海混响的建模与预报[J]. 海军工程大学学报 , 2009, 21 (2) :88–91. |
| [2] | 袁骏, 肖卉, 张明敏, 等. 双基地声呐海底混响面元划分与建模[J]. 探测与控制学报 , 2009, 31 (4) :1–4. |
| [3] | 张明辉. 三维环境海洋混响强度衰减规律研究[D]. 哈尔滨:哈尔滨工程大学, 2005:5-7. |
| [4] | 方世良. 海洋混响信号的序贯仿真[J]. 声学技术 , 1996, 15 (3) :101–104. |
| [5] | ABRAHAM D A, LYONS A P. Reverberation envelope statistics and their dependence on sonar bandwidth and scattering patch size[J]. IEEE journal of Oceanic Engineering , 2004, 29 (1) :126–137. DOI:10.1109/JOE.2004.824039 |
| [6] | ABRAHAM D A, LYONS A P. Simulation of non-rayleigh reverberation and clutter[J]. IEEE Journal of Oceanic Engineering , 2004, 29 (2) :347–362. DOI:10.1109/JOE.2004.828202 |
| [7] | 蔡平, 梁国龙, 葛凤翔, 等. 界面混响信号的仿真研究[J]. 哈尔滨工程大学学报 , 2000, 21 (4) :31–35. |
| [8] | 陈文剑, 孙辉, 朱建军, 等. 基于分数阶傅里叶变换混响抑制的目标回波检测方法[J]. 声学学报 , 2009, 34 (5) :408–415. |
| [9] | 郭熙业, 苏绍璟, 王跃科. 海底混响统计建模与仿真方法研究[J]. 兵工学报 , 2009, 30 (7) :940–944. |
| [10] | 郭熙业, 苏绍璟, 王跃科. 基于射线理论的海底混响建模研究[J]. 声学技术 , 2009, 28 (3) :203–207. |
| [11] | 姚万军, 蔡志明. 基于简正波的浅海混响序列仿真[J]. 声学技术 , 2009, 28 (1) :25–28. |
| [12] | 姚万军, 蔡志明, 卫红凯. 浅海混响建模的声束跟踪理论[J]. 声学学报 , 2009, 34 (3) :223–228. |
| [13] | ZHANG M H, SUN H, CHEN W J. Simulation model of bottom reverberation signals for horizontal bistatic receiving array[C]//Proceedings of 2008 IEEE International ultrasonics symposium. Beijing:IEEE, 2008:1437-1440. |
| [14] | ABRAHAM D A, LYONS A P. Exponential scattering and K-distributed reverberation[C]//Proceedings of 2001 MTS/IEEE Conference and Exhibition. Honolulu, HI:IEEE, 2001, 3:1622-1628. |
 2016, Vol. 38
2016, Vol. 38
