近年来,随着新型稀土永磁材料的出现,以及电机技术、控制技术和精密制造等技术的发展,电动技术得到了突破,许多国家开展了电力传动装置取代液压传动装置的研究,其中将电动伺服舵机取代液压舵机作为重要研究内容,用以降低操舵噪声[1-2]。
电动伺服舵机与液压舵机相比,结构组成有很大的不同,将采用操控性更好的伺服电机和高效、高可靠性的减速器,组成简单,无复杂的油源、阀组、管路等[3-5]。
由于原理、组成发生了变化,电动伺服舵机的操纵性能相对液压舵机也有所不同,为掌握这种性能,本文针对所提出的一种电动伺服舵机方案开展研究,以掌握其操纵性能。
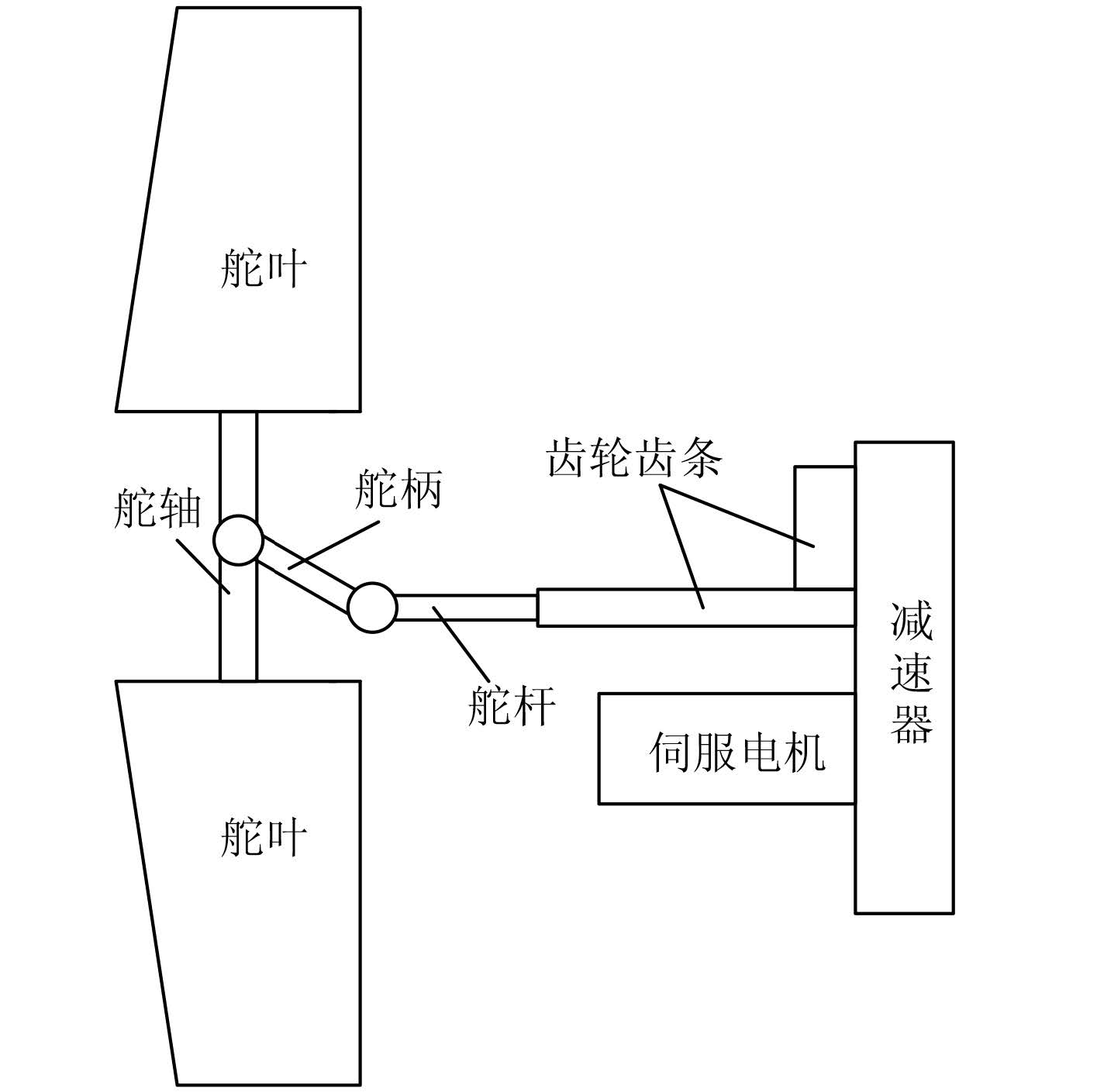
1 船用电动舵机方案图 1 所示为船用电动舵机示意图,伺服舵机主要由伺服电机和减速器及其控制器组成,伺服电机通过减速器减速后带动齿轮齿条机构,转换为直线运动,从而推拉舵杆、舵柄,使舵叶转动,改变船舶的航向。
|
图 1 电动伺服舵机示意图 Fig. 1 Schematic of the electro-servo rudder actuator |
该伺服舵机的主要性能指标如表 1 所示。
|
|
表 1 伺服舵机主要性能指标 Tab.1 Main performance values of the servo rudder actuator |
为达到上述指标,伺服电机选择了直流力矩电机,减速器为谐波齿轮减速器[6-7]。其主要参数如表 2 所示。
|
|
表 2 电动伺服舵机的基本配置 Tab.2 Basic configuration of the electro-servo rudder actuator |
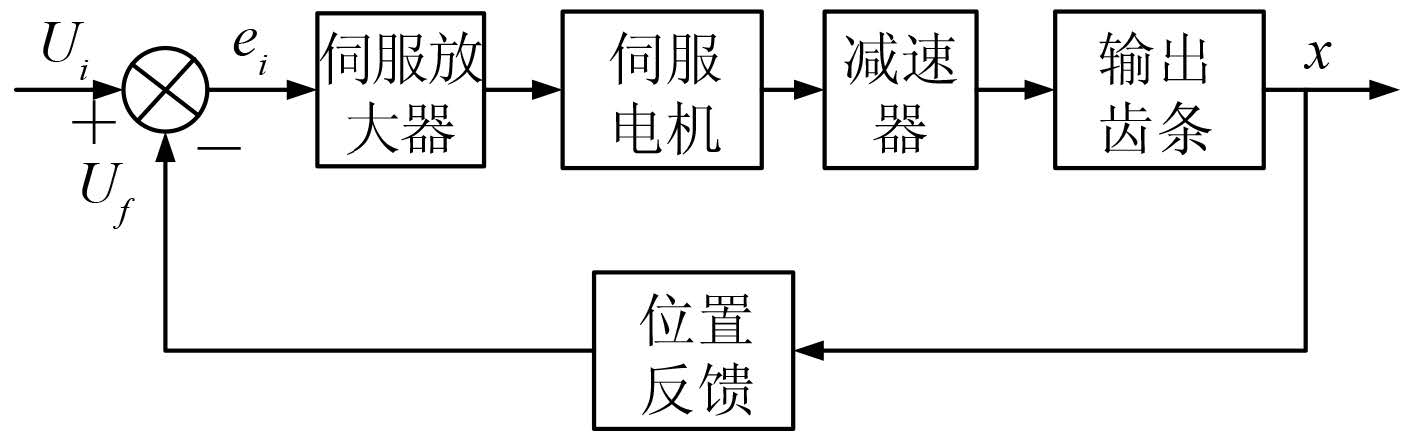
电动伺服舵机的控制框图如图 2 所示,本质上来说是一个位置控制系统,检测到的位置信号反馈给伺服放大器,其值与给定信号的差值用来控制伺服电机的转角,最终使舵叶转至目标角度。
|
图 2 电动伺服舵机控制框图 Fig. 2 Control diagram of the electro-servo rudder actuator |
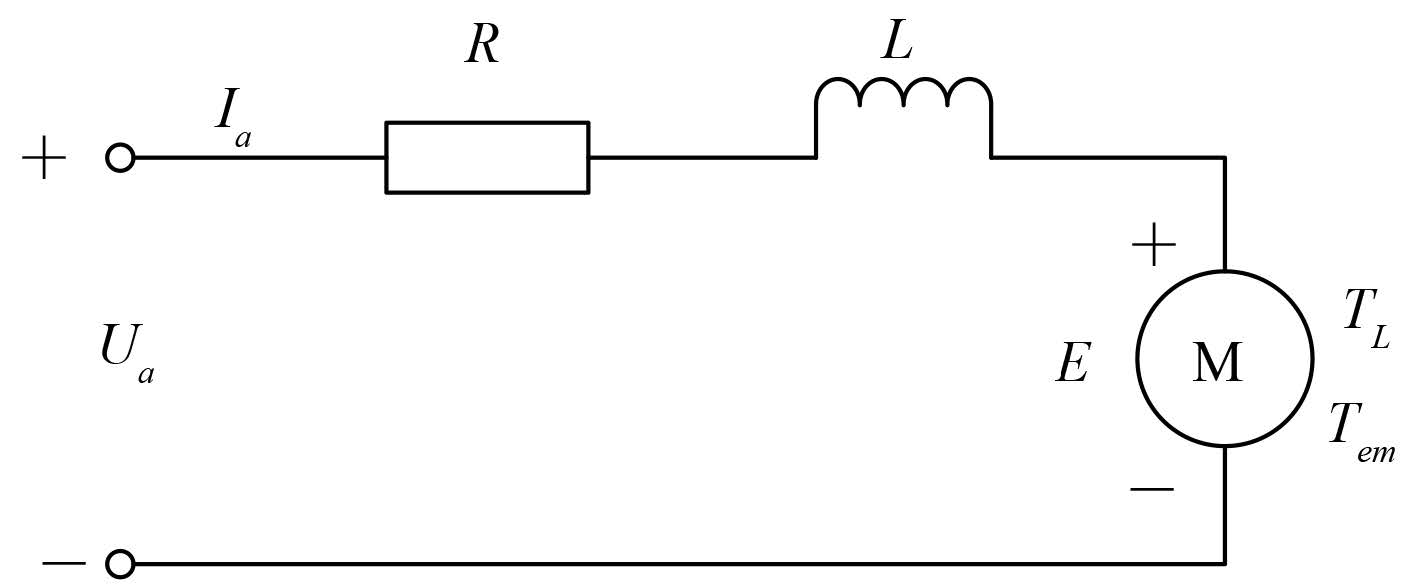
伺服电机的等效电路如图 3 所示。伺服电机电枢回路的微分方程如式(1)~ 式(4)所示:
| $ {U_{{a}}} = R{I_{{a}}} + L\frac{{{\text{d}}{I_{{a}}}}}{{{\text{d}}t}} + E\text{,} $ | (1) |
| $ E = {C_{{e}}}n\text{,} $ | (2) |
| $ {T_{{{em}}}} - {T_{{L}}} = \frac{{G{D^2}{\text{d}}n}}{{375{\text{d}}t}}\text{,} $ | (3) |
| $ {T_{{{em}}}} = {C_{{T}}}{I_{{a}}}\text{。} $ | (4) |
|
图 3 伺服电机等效电路 Fig. 3 Equivalent circuit of the servo electric motor |
式(1)为假定电流连续时的主电路电势方程,式(2)为额定励磁下的感应电动势,式(3)为忽略空载转矩的牛顿动力学定律,式(4)为额定励磁下的电磁转矩。
定义以下时间常数:
电枢回路电磁时间常数 ${T_{\text{l}}} = \displaystyle \frac{L}{R}$;
电力拖动系统的机电时间常数 ${T_{{m}}} = \displaystyle \frac{{G{D^2}R}}{{375{C_{{e}}}{C_{{T}}}}}$。
Tl 和 Tm 分别表示电气惯性与机械惯性的影响。代入式(1)~ 式(4)整理可得式(5)和式(6):
| $ {U_{{a}}} - E = R({I_{{a}}} + {T_{\text{l}}}\frac{{{\text{d}}{I_{{a}}}}}{{{\text{d}}t}})\text{,} $ | (5) |
| $ {I_{{a}}} - {I_{{{aL}}}} = \frac{{{T_{{m}}}}}{R}\frac{{{\text{d}}E}}{{{\text{d}}t}}\text{,} $ | (6) |
式中 IaL 为负载电流,其值为:
| $ {I_{{{aL}}}} = \frac{{{T_{{L}}}}}{{{C_{{T}}}}}\text{。} $ | (7) |
对式(5)和式(6)进行拉式变换,得到电压与电流间的传递函数为:
| $ \frac{{{I_{{a}}}\left( {\text{s}} \right)}}{{U\left( {\text{s}} \right) - E\left( {\text{s}} \right)}} = \frac{{1/R}}{{{T_1}{\text{s}} + 1}}\text{,} $ | (8) |
电流与电动势间的传递函数为:
| $ \frac{{E\left( {\text{s}} \right)}}{{{I_a}\left( {\text{s}} \right) - {I_{{{aL}}}}\left( {\text{s}} \right)}} = \frac{R}{{{T_{{m}}}{\text{s}}}}\text{。} $ | (9) |
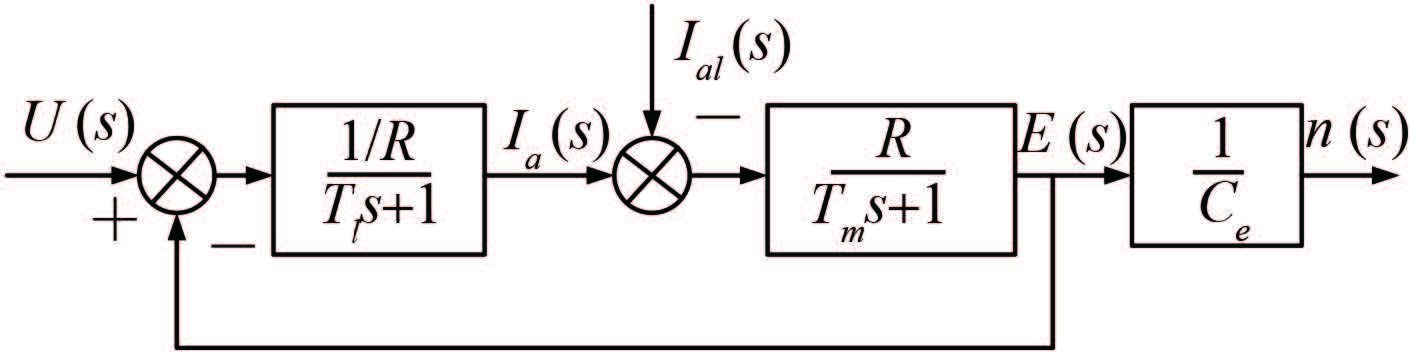
由式(8)和式(9)可得到直流伺服电机的动态结构如图 4 所示。
|
图 4 伺服电机动态模型 Fig. 4 Dynamic model of the servo electric motor |
其中:U(s)为输入的控制量;IaL(s)为扰动的输入。
当电机空载时(IaL = 0),即扰动为 0,简化图 4 得到电机系统空载时的等效结构如图 5 所示,此时电机等效为一个 2 阶环节的传递函数。
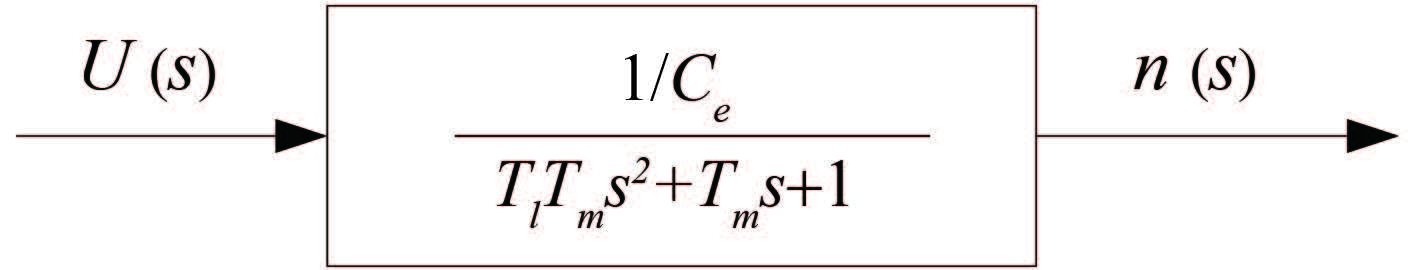
|
图 5 伺服电机简化模型 Fig. 5 Simplified model of the servo electric motor |
谐波齿轮的动态模型可等效为图 6。

|
图 6 谐波齿轮动态模型 Fig. 6 Dynamic model of the harmonic gear |
图中,Ke 为谐波齿轮减速器的刚度系数;Ja 为负载折算至谐波齿轮减速器的转动惯量;B 为阻尼系数;θ 为输出角度。
其中折算至谐波齿轮减速器的转动惯量 Ja 为:
| $ {J_{{a}}} = {{\rm{J}}_{{x}}} + \frac{{{J_1}}}{{j_1^2}} + \frac{{{J_L}}}{{j_L^2}} + m\frac{{{{\rm{v}}^2}}}{{{\rm{\omega }}_{{x}}^2}}\text{。} $ | (10) |
式中:Jx 为谐波齿轮减速器轴上的转动惯量;J1 为中间传动轴上的转动惯量;j1为谐波齿轮减速器与中间传动轴之间的速比;JL 为负载的转动惯量;jL 为谐波齿轮减速器与负载之间的速比;m 为负载的质量;v 为负载的直线运动速度;ωx 为谐波齿轮减速器的转速。
2.1.3 负载模型电动伺服舵机的负载包括舵叶、舵杆、舵柄及附连水质量等,可将其等效为图 7 所示的模型,模型中 m,B1,K 分别为负载等效质量、阻尼及刚度,经计算及参照经验公式,m 为 6 000 kg,B1 为 0.1,K 为 1E 13。

|
图 7 负载等效模型 Fig. 7 Load equivalent model |
完成上述建模后,为了更便于调整仿真参数,查看仿真结果,将上述模型作为后台,采用 Matlab Simulink 软件编制了仿真的图形用户界面(见图 8),在仿真界面中,可直观修改各期器件的参数,并得到时域和频域的仿真结果[8]。
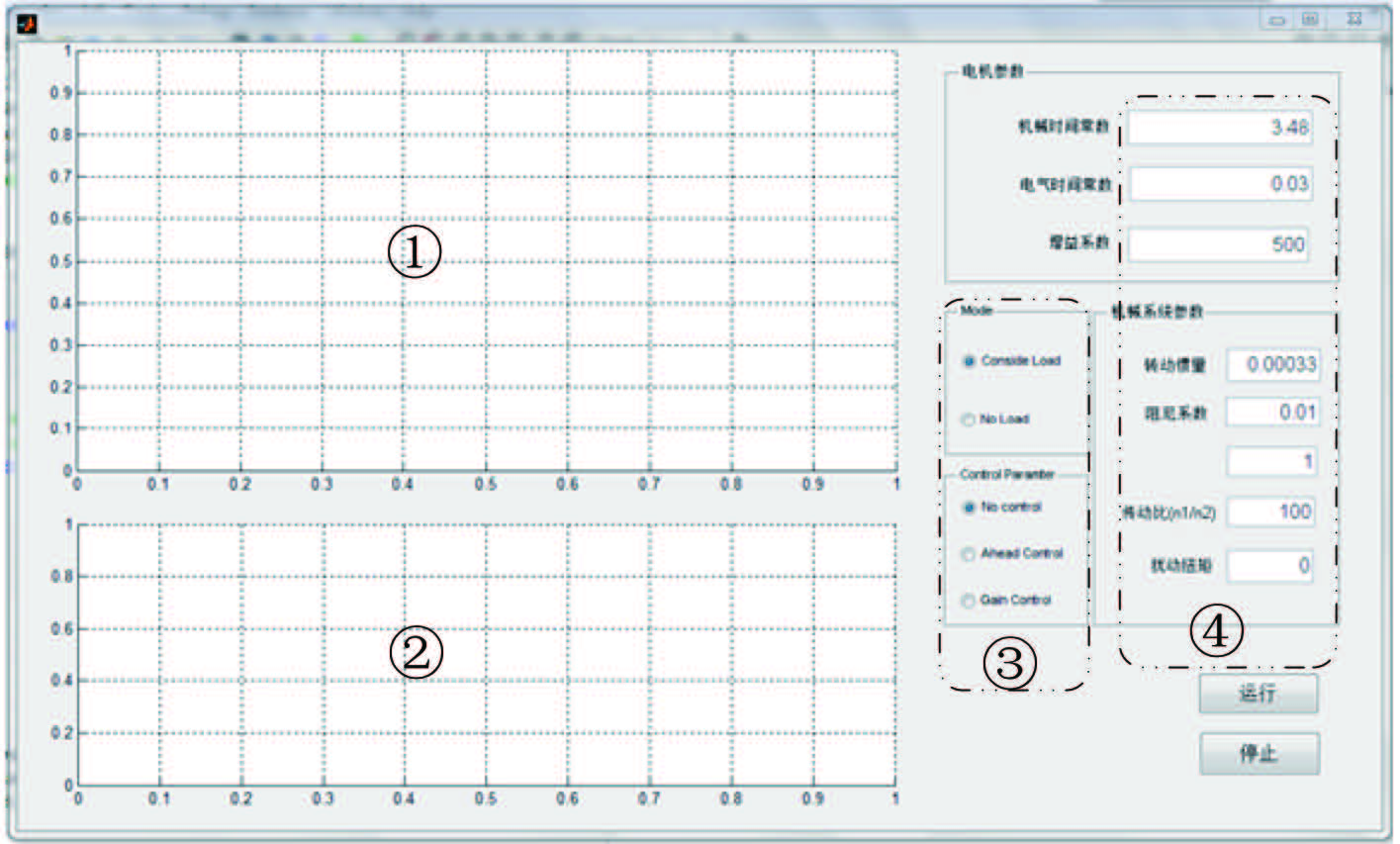
|
图 8 仿真界面 Fig. 8 Simulation interface |
图 8 中,①为波特图显示区,显示系统的幅值与相位的对数曲线图;②为时域波形显示区,在显示波特图的同时反映系统时域信号波形;③为操作选择区,主要有两类操作,第 1 类模式选择,考虑负载效应问题,目前是分别考虑空载与带负载时的情形,前者不考虑机械负载,仅分析驱动电机的特性,后者可按实际情况考虑电机驱动负载时的机电系统特性;第 2 类为控制选择,主要考虑控制器对整个系统的影响,目前分别考虑无附加控制、带前馈控制、以及带增益控制这 3 种不同的情况;④为参数输入区,可根据实际仿真的配置方案输入相应的参数,以满足仿真要求。
在该仿真软件中,可根据设计方案中给出的典型配置输入电机、减速器参数,或根据实际选型所获得的参数输入,也同样可得到仿真结果。
2.2.2 仿真结果基于上述模型和图形界面,对该电动舵机在空载、带载、前馈控制、增益控制等各种模式下的操纵响应进行仿真(如图 9 所示为带负载增益控制下的系统响应)。
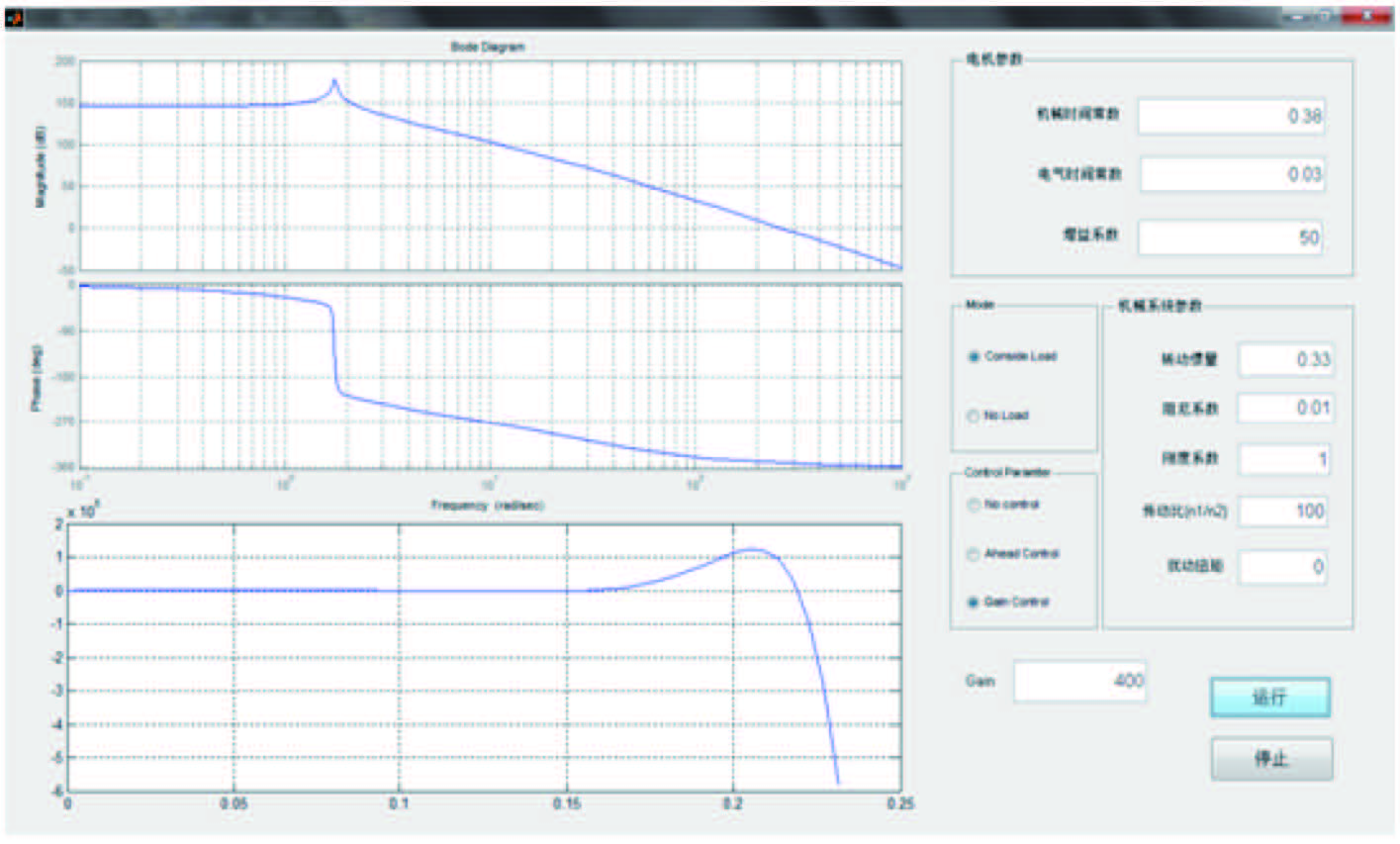
|
图 9 带负载增益控制下的系统响应 Fig. 9 System response with load under gain control |
根据仿真结果,对系统的操纵性能进行分析如下:
1)影响系统稳定性的因素主要有阻尼、刚度等参数,在电动伺服舵机中,选用常用的直流力矩电机和谐波齿轮,系统的幅值裕度可达到 5 dB,相位裕度可达到 45°,满足稳定性的条件。
2)对于电动伺服舵机,影响精度的主要因素有伺服电机、谐波齿轮的刚度系数等,当刚度系数越大时,稳态误差越小,精度越高,对于直流力矩电机和谐波齿轮构成的电动伺服舵机,操舵舵角的稳态误差可控制在 0.2°(对应齿条直线位移为 0.2 mm),可满足舵系统这个大惯性系统的操作要求。
3)响应快是电动伺服系统的特点之一,影响其频响的主要因素有电机的电磁时间常数、机电时间常数、转动惯量、谐波齿轮的转动惯量等,根据本系统选择的元件类型,舵机的频响可大于 10 Hz。而负载为大惯性系统,其固有频率小于 1 Hz,因此电动伺服舵机的相应性能可满足操舵的需求。
综上,以直流力矩电机和谐波齿轮为主构成的电动伺服舵机的稳定性、精度和响应均可满足操纵要求。
3 结 语电动伺服舵机由于组成简单、维护方便、噪声低等特点,正逐渐在船舶上得以应用,取代液压舵机。本文针对所提出的一种电动伺服舵机方案开展了操纵性能的研究,建立了该舵机的仿真模型,编制了图形用户仿真界面,仿真结果表明,该电动舵机性能可满足船舶的操纵要求。
| [1] |
谢俊超, 肖清, 花靖. 船用新型电动舵机可行性研究[J]. 舰船科学技术 , 2013, 35 (10) :78–81.
XIE Jun-chao, XIAO Qing, HUA Jing. Research on the new marine electro-mechanical actuator feasibility[J]. Ship Science and Technology , 2013, 35 (10) :78–81. |
| [2] |
张阳阳, 邢继峰, 彭利坤, 等. 电动舵机用电动缸滚珠丝杠振动特性[J]. 舰船科学技术 , 2013, 35 (12) :29–31.
ZHANG Yang-yang, XING Ji-feng, PENG Li-kun, et al. Ball screw vibration characteristic of electric cylinder used in electric helm[J]. Ship Science and Technology , 2013, 35 (12) :29–31. |
| [3] |
王灿, 马瑞卿, 谭博, 等. 直流电动舵机伺服作动系统研制[J]. 微特电机 , 2008, 36 (10) :25–27.
WANG Can, MA Rui-qing, TAN Bo, et al. Design of DC electric steering engine servo actuator system[J]. Small & Special Electrical Machines , 2008, 36 (10) :25–27. |
| [4] |
李福瑞, 李擎, 夏嵩. 直流电动舵伺服系统设计与研究[J]. 北京信息科技大学学报 , 2010, 25 (1) :42–45.
LI Fu-rui, LI Qing, XIA Song. Design and research of DC electric rudder servo system[J]. Journal of Beijing Information Science and Technology University , 2010, 25 (1) :42–45. |
| [5] |
张新华. 完全双余度电动舵机系统的研究与设计[J]. 微电机 , 2006, 39 (2) :32–34.
ZHANG Xin-hua. A research and design of entire dual redundancy electro-mechanical actuator[J]. Micromotors , 2006, 39 (2) :32–34. |
| [6] |
董超奎, 段强. 微型无刷直流电动机在电动操舵系统中的应用[J]. 微电机 , 2006, 39 (6) :22–25.
DONG Chao-kui, DUAN Qiang. Application of micro brushless DC motor on elector rudder system[J]. Micromotors , 2006, 39 (6) :22–25. |
| [7] |
王建军, 杨宏源, 白会彦. 谐波齿轮传动在伺服机构中的应用与计算[J]. 战术导弹控制技术 , 2003 (1) :43–47.
WANG Jian-jun, YANG Hong-yuan, BAI Hui-yan. Computation and application of harmonic gear drive in a servo system[J]. Control Technology of Tactical Missile , 2003 (1) :43–47. |
| [8] |
霍学亮, 任光, 张均东, 等. 基于Simulink的船舶舵机系统的建模与动态仿真[J]. 大连海事大学学报 , 2007, 33 (S) :74–76.
HUO Xue-liang, REN Guang, ZHANG Jun-dong, et al. Modeling and dynamic simulation of steering gear system of ship based on Simulink[J]. Journal of Dalian maritime university , 2007, 33 (S) :74–76. |
 2016, Vol. 38
2016, Vol. 38
