2. 中国船舶科学研究中心, 江苏 无锡, 214082
2. China Ship Scientific Research Center, Wuxi 214082, China
船舶在海上作业过程中发生故障而无法自行回港时,通常的救援方式主要有拖带救援和装载救援。当故障船损毁严重不具备长距离拖带条件或急需在海上进行应急维修时,只能依靠大吨位的半潜船进行海上的应急装载救援。半潜船是专门从事海上运输海洋平台、舰艇、龙门吊、预制桥梁构件等大型设备的特种海运工程船,具有甲板开阔、载重量大、可下潜装载的特点。
陈志强等[1]针对海洋工程中常见的半潜船开展研究,通过数值方法分析半潜船的附加质量与振动性能。刘汉明等[2-5]针对故障船的运动规律进行研究,建立了风、浪、流联合作用下的水面失事船舶运动的计算模型,同时针对浮筒打捞沉船的运动计算问题进行研究,考虑了影响沉船上浮运动的因素,建立沉船上浮运动的计算模型,通过对模型进行数值求解,得到沉船上浮运动在各个时刻的参数值。何国明[6-7]针对沉船的上浮运动开展分析,同时研究了浮筒的浮力膨胀对沉船打捞的影响,分析沉船打捞过程的系统运动特性。祝传刚等[8]提出了工程化搜救方案辅助设计的思想,并根据系统设计目标,对搜救辅助决策系统的整体架构、系统模块进行了详细的设计。任凯等[9]针对半潜式起重船在失事舰船救援方面的应用进行研究,分析半潜式起重船救援受损船的适用条件、人员组织以及安全保障要求,分析国外操作中的具体方法与成功经验。总结研究现状,当前针对半潜船装载故障船的研究相对较少,针对装载时两船相对运动特性的研究有待深入开展。
应用半潜船在海上进行故障船的救援装载,应首先对两船在一定海洋环境下的运动响应进行研究,根据研究结果分析装载作业的可行性,并制定海上装载方位、程序和危机处置预案等合理的方案。论文以 20 000 吨级半潜船与 3 000 吨级故障船为研究对象,应用数值分析软件 AQWA,对两船的运动响应进行数值模拟研究。
1 基本理论对于不可压缩的理想流体,在无旋流场中,速度势满足拉普拉斯方程,解出速度势,根据方程 $\mathop V\limits^ \to = \nabla \phi$,求解得出速度分布,由拉格朗日方程得到船体表面的压力分布[10-12]。
一阶波浪力的速度势为:
| $ \phi = \varphi {e^{ - i\omega t}} = [({\varphi _{_I}} + {\varphi _{_d}}) + \sum\limits_{j = 1}^6 {{\varphi _{_j}}{x_{_j}}}]{e^{ - i\omega t}}\text{,} $ | (1) |
式中:ω 为规则波频率;φI 为入射势;φd 为绕射势;φj 为六自由度运动方向的速度势(j=1~6)。
入射势为:
| $ {\varphi _{_I}}{e^{ - i\omega t}} = \displaystyle \tfrac{{ - ig\zeta ch[k(d + z)]{e^{ik(X\cos \theta + Y\sin \theta )}}{e^{ - i\omega t}}}}{{\omega ch(kd)}} \text{。} $ | (2) |
式中:k 为波数,由 ω2 = gkth(kd)求得;d 为水深;ζ 为入射波幅。
解得一阶波浪力速度势后,压力分布由伯努利方程求得:
| $ P = - \rho \frac{{\partial \varphi }}{{\partial t}}\text{,} $ | (3) |
沿船体的湿表面积分得到一阶波浪力如下:
| $ {F_j} = - \int\limits_s {P{n_j}{\rm d}s} = - \int\limits_s {i\omega \rho ({\varphi _I} + {\varphi _d})} {n_j}{\rm d}s \text{。} $ | (4) |
AQWA-LINE 通过数值求解以下运动方程,分别计算得出半潜船和故障船在规则波作用下的运动响应幅值算子(RAO):
| $ Ms(\omega )\ddot X + Ma(\omega )\ddot X + C(\omega )\dot X + Ks(\omega )X = F(\omega ) \text{。} $ | (5) |
式中:Ms 为结构质量;Ma 为水动力附加质量;C 为系统线性阻尼;Ks 为系统总刚度;ω为波频;F 为系统所受到的波浪力;X 为幅值响应算子(RAO)。
2 数值模拟模型及工况 2.1 数值模拟模型按照某型 20 000 吨级半潜船与 3 000 吨级故障船的主体线型建立数值模拟模型。半潜船长 156 m,船宽 36 m,型深 10 m;故障船长 75 m,船宽 8.4 m,型深 8 m。按照两船的型线特征及设备布置,明确数值模拟模型的重心位置,数值模拟模型如图 1 所示。

|
图 1 数值模拟模型 Fig. 1 Numerical simulation model |
根据半潜船甲板上绞车的布置情况,在数值模拟模型上对故障船施加约束,半潜船与故障船通过 4 根系缆连接,系缆长 35.5 m,张力为 15 t。在故障船上与半潜船的甲板面上分别设定 4 个监测点,监测点的分布如图 2 所示。

|
图 2 半潜船与故障船的监测点分布图 Fig. 2 Distribution of monitoring points |
数值计算的环境工况,基于开阔海域充分发展的海浪,选用 JONSWAP 谱,该波浪谱式为:
| $ \begin{aligned} {{S}_{\xi }}(\omega )= & 487\left[1-0.287\ln \gamma \right]\frac{H_{s}^{2}}{T_{p}^{4}{{\omega }^{5}}} \\ & \exp \left\{ -\frac{1948}{{{({{T}_{p}}\omega )}^{4}}} \right\}{{\gamma }^{\exp \left[-\frac{{{(0.159\omega {{T}_{p}}-1)}^{2}}}{2{{\sigma }^{2}}} \right]}}\text{。} \\ \end{aligned} $ | (6) |
式中:σ 为峰形参数,当 ω ≤ ωp 时,取 0.07;当 ω > ωp 时,取 0.09,谱峰提升因子 γ 取 3.0。适用装载的最大海况为 3 级上限,取有义波高 Hs = 1.25 m。
浪向考虑顶浪、横浪、斜浪 3 个主要的来浪方向;风选用 NPD 谱,风向的设定与浪向一致,10 m 高度处的平均风速为 10.7 m/s;流速为 1 m/s,方向与风向、浪向一致。环境工况参数见表 1。
|
|
表 1 环境工况参数 Tab.1 Environmental criteria |
基于实际的船型建立数值模拟系统,考虑设定 3 级海况下的风浪流环境参数,应用 AQWA-DRIFT 开展 3 h 不规则波作用下的时域计算,得出半潜船与故障船在装载过程中的运动响应,并对比随着半潜船的起浮,故障船底部与半潜船甲板的间距从 3 m 接近至 2 m 过程中两船的运动响应变化规律。
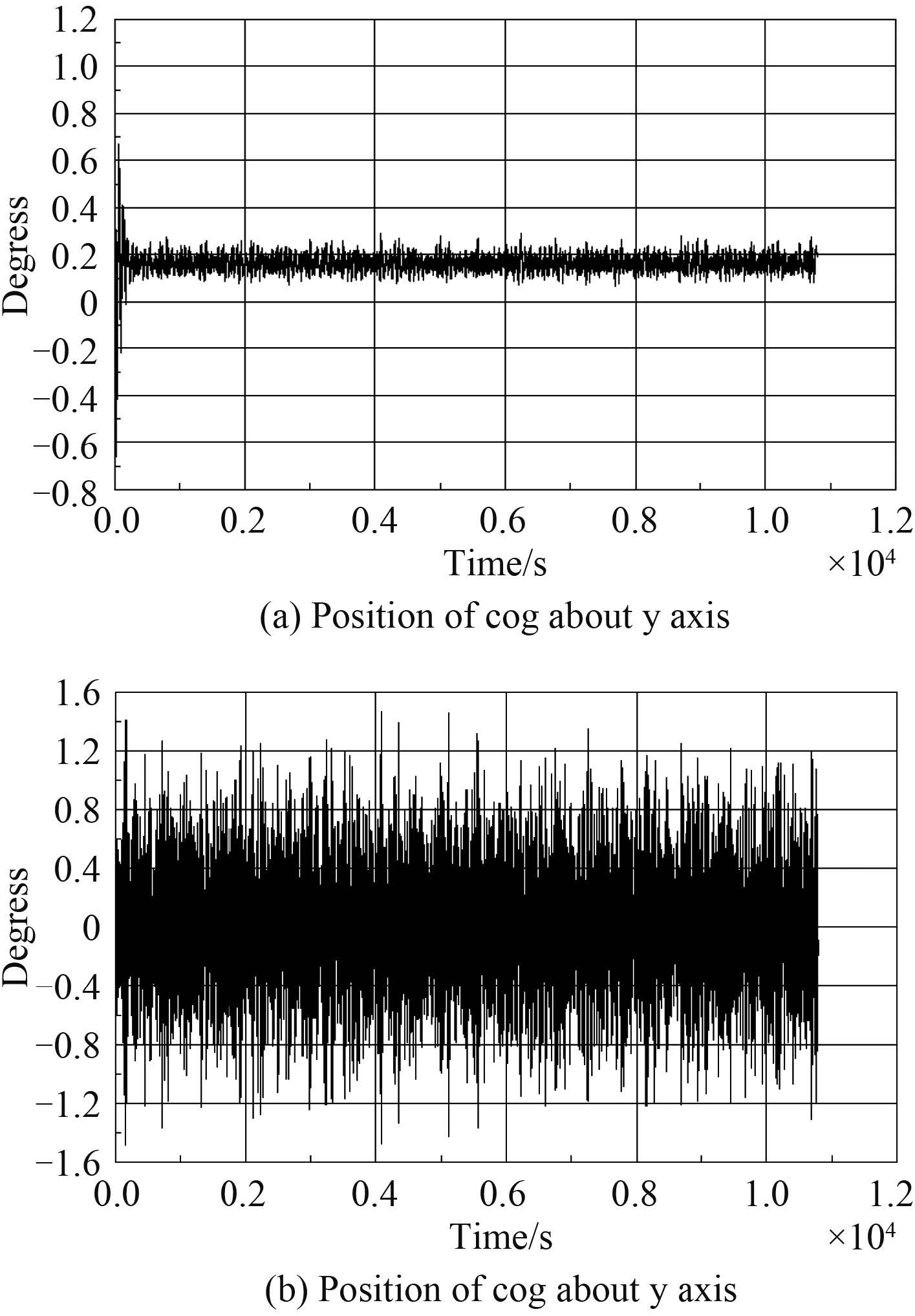
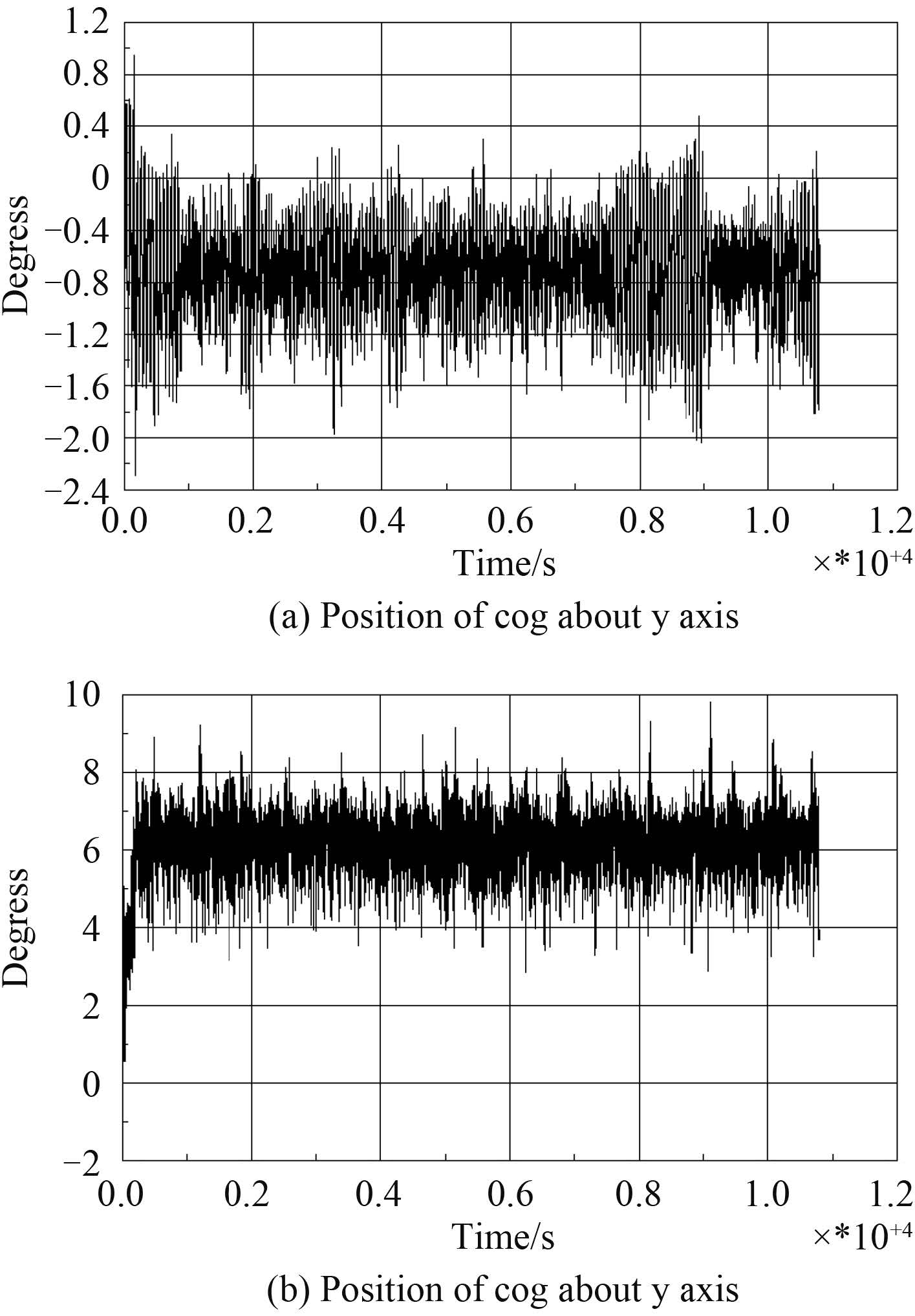
3 数值分析 3.1 两船运动响应特性针对两船的运动响应开展分析,图 3 和图 4 为半潜船起浮前,即两船 3 m 间距时的运动响应结果,图 3所示为顶浪状态下的两船纵摇运动时历曲线,图 4 所示为横浪状态下的两船横摇运动时历曲线,横坐标为 3 h 的时间历程,s;纵坐标为运动响应,(°)。
|
图 3 半潜船和故障船纵摇时历曲线(顶浪 180°) Fig. 3 Time-history curve of the two ships pitch motion(wave incidence 180°) |
|
图 4 半潜船和故障船横摇时历曲线(横浪 90°) Fig. 4 Time-history curve of the two ships roll motion(wave incidence 90°) |
改变半潜船的吃水深度,模拟半潜船上浮至距离故障船底部 2 m 的状态进行数值计算,可以得到规律类似的时历曲线,并对半潜船与故障船的运动响应最大值进行统计,结果如表 2 和表 3 所示。
|
|
表 2 半潜船和故障船运动响应最大值(半潜船起浮前) Tab.2 Maximum value of the two ships motion responses(before floating) |
|
|
表 3 半潜船和故障船运动响应最大值(半潜船起浮后) Tab.3 Maximum value of the two ships motion responses(after floating) |
对比半潜船起浮前后不同间距下两船各自的运动响应,得到规律:顶浪作业下,故障船的横荡、垂荡、横摇及首摇运动均很小,两船的运动响应主要体现在纵荡与纵摇,随着半潜船的上浮,故障船的纵荡运动响应减小,纵摇角的最大值增大;横浪作业下,半潜船与故障船的运动响应主要体现在横荡和横摇,随着横浪的不断作用,两船产生方向上的偏移,发生纵荡、首摇运动,同时随着半潜船的上浮,故障船的纵荡幅度减小,而首摇角增大;斜浪作业下,半潜船与故障船在横向与纵向均产生运动,随着半潜船的上浮,两船六自由度的运动响应数值均增大,且在斜浪作用下,故障船的纵摇运动较为突出。
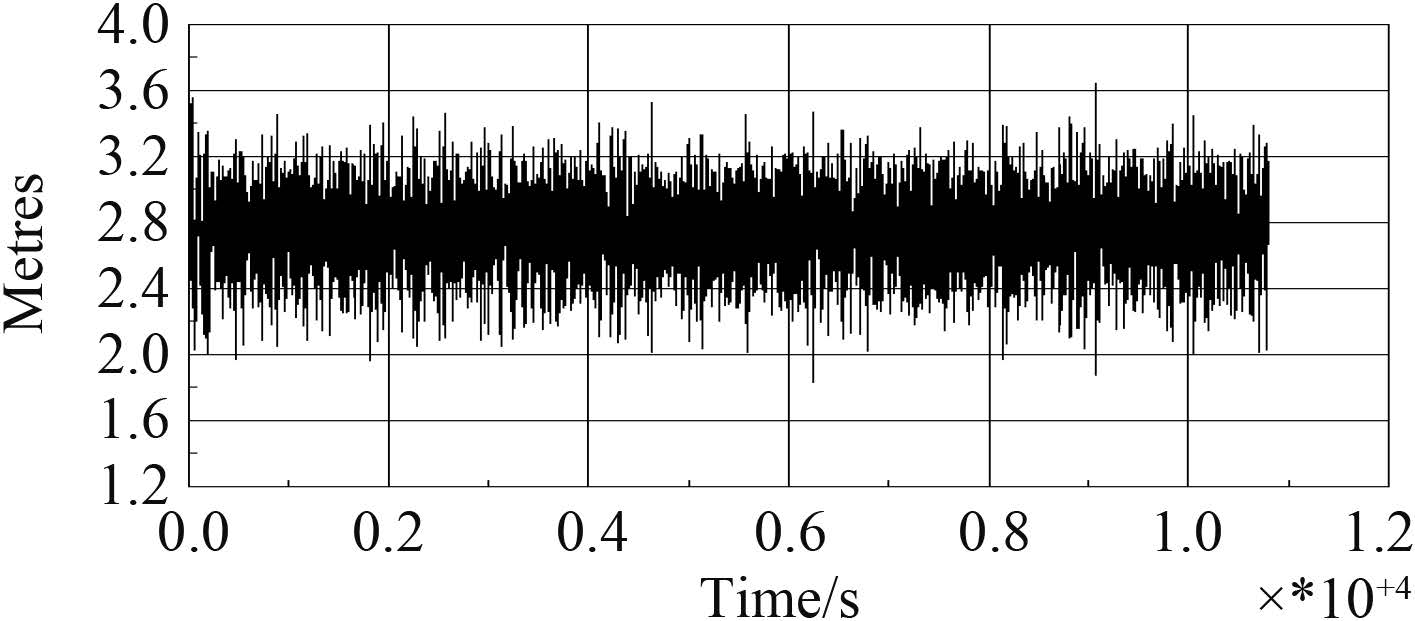
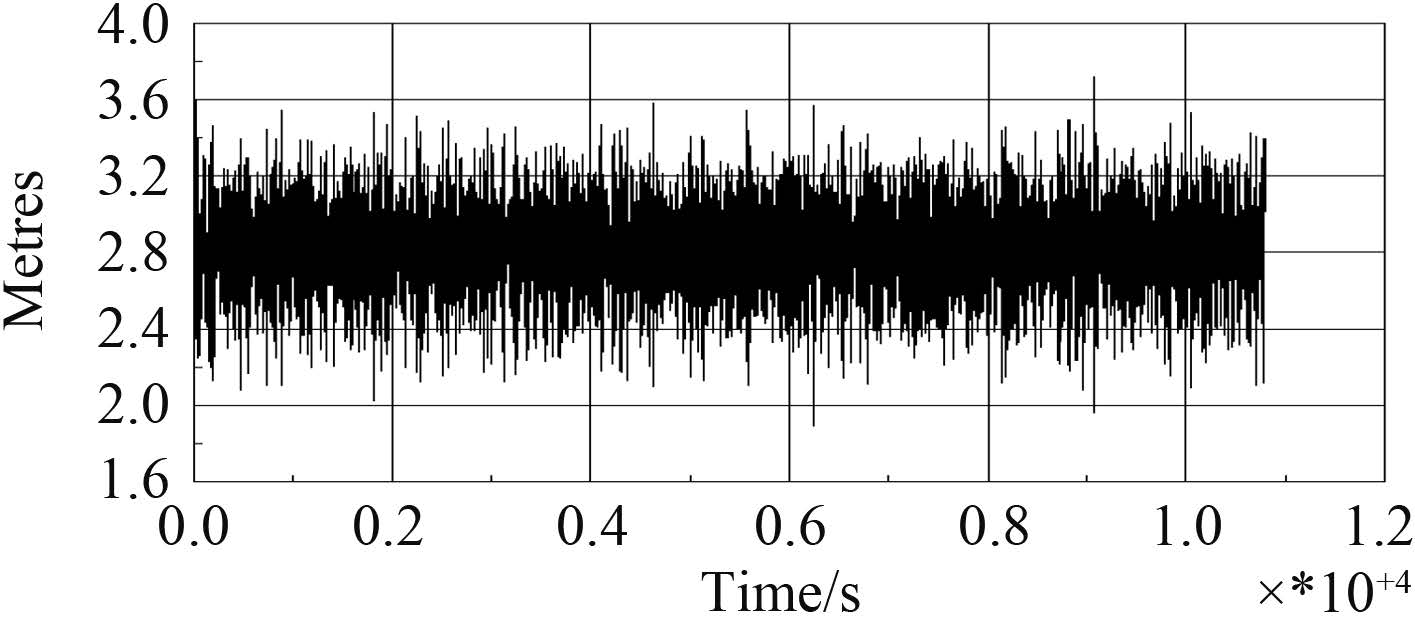
3.2 装载作业系统特性基于数值模拟计算,得到各监测点的垂向、横向及纵向间距的时历规律,举例两船 3 m 间距的作业状态,图 5 与图 6 分别为横浪时 2# 监测点与 3# 监测点的垂向间距变化时历曲线。
|
图 5 故障船与半潜船甲板的 2#监测点垂向间距变化时历曲线(横浪 90°) Fig. 5 Time-history curve of the vertical spacing between 2# monitoring points on two ships(wave incidence 90°) |
|
图 6 故障船与半潜船甲板的 3#监测点纵向间距变化时历曲线(横浪 90°) Fig. 6 Time-history curve of the vertical spacing between 3# monitoring points on two ships(wave incidence 90°) |
分析半潜船起浮前后,半潜船与故障船的相对升沉运动、相对横向偏移及相对纵向偏移,最大值的统计结果参见表 4 与表 5。
|
|
表 4 半潜船与故障船相对运动统计结果(半潜船起浮前) Tab.4 Statistical results of relative motions(before floating) |
|
|
表 5 半潜船与故障船相对运动统计结果(半潜船起浮后) Tab.5 Statistical results of relative motions(after floating) |
对比半潜船起浮前后不同间距下的两船相对运动,得到规律:迎浪条件下,两船相对升沉运动的幅度较小,随着半潜船起浮,两船的距离接近,相对升沉的幅度增大;在横浪条件下,相对横向偏移较小,随着两船距离的接近,横向偏移的幅度增大;对于斜浪条件,两船的相对纵向偏移较小,半潜船起浮过程中两船的距离接近,对纵向偏移增大。
4 结 语论文应用数值计算的方法,分析半潜船与故障船的运动响应特性,针对装载的方案提出 3 点结论:
1)装载方案实施时,两船均处于顶浪的状态为佳;
2)随着半潜船的起浮装载,半潜船的甲板与故障船的距离逐渐接近,两船的相对运动幅值均增加,因此在实际的装载过程中需要加强对故障船装载作业的位置控制,辅以防撞与减震等措施;
3)考虑到两船相对横向偏移较大,对装载过程的影响较大,建议在设计中加装横向的牵引装置,对故障船的横向运动加以约束,提高装载坐墩的效率。
论文针对半潜船装载故障船的水动力特性开展研究,应用数值模拟方法,建立两船系统的数值模型,分析两船的运动响应特性,研究结果对实际装载方案的制定与优化具有参考价值。论文重点开展运动特性方面的分析,相关的半潜船装载故障船的受力特性可以在后续的工作中开展深入研究。
| [1] |
陈志强, 周力. 半潜船振动特性[J]. 舰船科学技术 , 2014, 36 (6) :31–37.
CHEN Zhi-qiang, ZHOU Li. Vibration characteristics analysisof semi-submerged ship[J]. Ship Science and Technology , 2014, 36 (6) :31–37. |
| [2] |
刘汉明, 卢镇. 沉船上浮运动实域计算与分析[J]. 救捞与潜水 , 1998 (1) :6–12.
LIU Han-ming, LU Zhen. Investigation and analysis of the sunken ship floating motion in time domain[J]. Salvage and Diving , 1998 (1) :6–12. |
| [3] |
刘汉明. 浮筒打捞沉船上浮过程的稳性研究[D]. 武汉:海军工程学院, 1991.
LIU Han-ming. Stability study on the buoy floatation process of salvaging a sunken ship[D]. Wuhan:Naval University of Engineering, 1991. |
| [4] |
刘汉明, 苗兰森, 臧海鹏. 风、流、浪联合作用下的水面失事难船漂流运动仿真模型研究[C]//第四届中国国际救捞论坛论文汇编. 海南博鳌:中国航海学会, 2007:86-89.
LIU Han-ming, MIAO Lan-shen, ZANG Hai-peng. Research on the drift movement imitating models of surface wrecking ship under united effect of wind, flow and wave[C]//Proceedings of the 4th C.I.R.S.C. Boao Hainan:China Institute of Navigation, 2007:86-89. |
| [5] |
刘汉明. 打捞力区间估算的沉船打捞起浮方案设计方法研究[C]//救捞专业委员会1993年学术交流会论文集. 厦门:中国航海学会, 1993.
LIU Han-ming. Research on the salvage force interval estimation of wreck salvage plan design method[C]//Proceedings of the China international rescue and salvage conference. Xiamen:China Institute of Navigation, 1993. |
| [6] |
何国明. 沉船上浮运动分析[J]. 救捞与潜水 , 1996 .
HE Guo-ming. Analysis of the sunken ship floating motion[J]. Salvage and Diving , 1996 . |
| [7] |
何国明. 论浮筒的浮力膨胀对沉船打捞的影响[J]. 救捞与潜水 , 1996 .
HE Guo-ming. Study on the buoy expansion effects on the wreck removal[J]. Salvage and Diving , 1996 . |
| [8] |
祝传刚, 刘汉明, 臧海鹏, 等. 海上失事船舶搜寻救助辅助决策系统设计[C]//救捞专业委员会2006年学术交流会论文集. 昆明:中国航海学会, 2006.
ZHU Chuan-gang, LIU Han-ming, ZANG Hai-peng, et al. Auxiliary design system of maritime search and rescue[C]//Proceedings of the China international rescue and salvage conference. Kunming:China Institute of Navigation, 2006. |
| [9] |
任凯, 程智斌. 半潜式起重船在受损舰船援救中的应用[C]//救捞专业委员会2005年学术交流会论文集. 长江三峡:中国航海学会, 2005.
REN Kai, CHENG Zhi-bin. The application of heavy lift using in wreckage warship salvage[C]//Proceedings of the China international Rescue and Salvage conference. Three Gorges of Yangtze River:China Institute of Navigation, 2005. |
| [10] |
夏国泽.
船舶流体力学[M]. 武汉: 华中科技大学出版社, 2003 .
XIA Guo-ze. Ship hydrodynamics[M]. Wuhan: Huazhong University of Science and Technology Press, 2003 . |
| [11] |
戴遗山, 段文洋.
船舶在波浪中运动的势流理论[M]. 北京: 国防工业出版社, 2008 .
DAI Yi-shan, DUAN Wen-yang. Potential flow theory of ship motions in waves[M]. Beijing: National Defend Industry Press, 2008 . |
| [12] | MOLIN B. Hydrodynamique des structures offshore[M]. Beijing: National Defend Industry Press, 2012 . |
 2016, Vol. 38
2016, Vol. 38
