2. 船舶振动噪声重点实验室, 湖北 武汉 430033
2. National Key Laboratory on Ship Vibration & Noise, Wuhan 430033, China
为控制军事舰艇的振动和噪声,提高其主要技术指标隐身性能,舰艇上的动力机械往往大量采用各型隔振装置[1],目前舰船上使用的隔振器主要有橡胶类隔振器、金属弹簧隔振器、钢丝绳隔振器和气囊隔振器等。
气囊隔振器是一种性能优良的隔振元件,它的固有频率低[2],通常小于 5 Hz。因此与金属弹簧隔振器、钢丝绳隔振器、橡胶隔振器等其他形式的隔振器相比,气囊隔振器的隔振性能更好。
橡胶隔振器是应用最为广泛的一类隔振器,它具有结构紧凑、工艺性好、成本低等优点,橡胶的内部阻尼较大,对于抑制共振振幅和减弱冲击引起的振动有显著效果[3]。
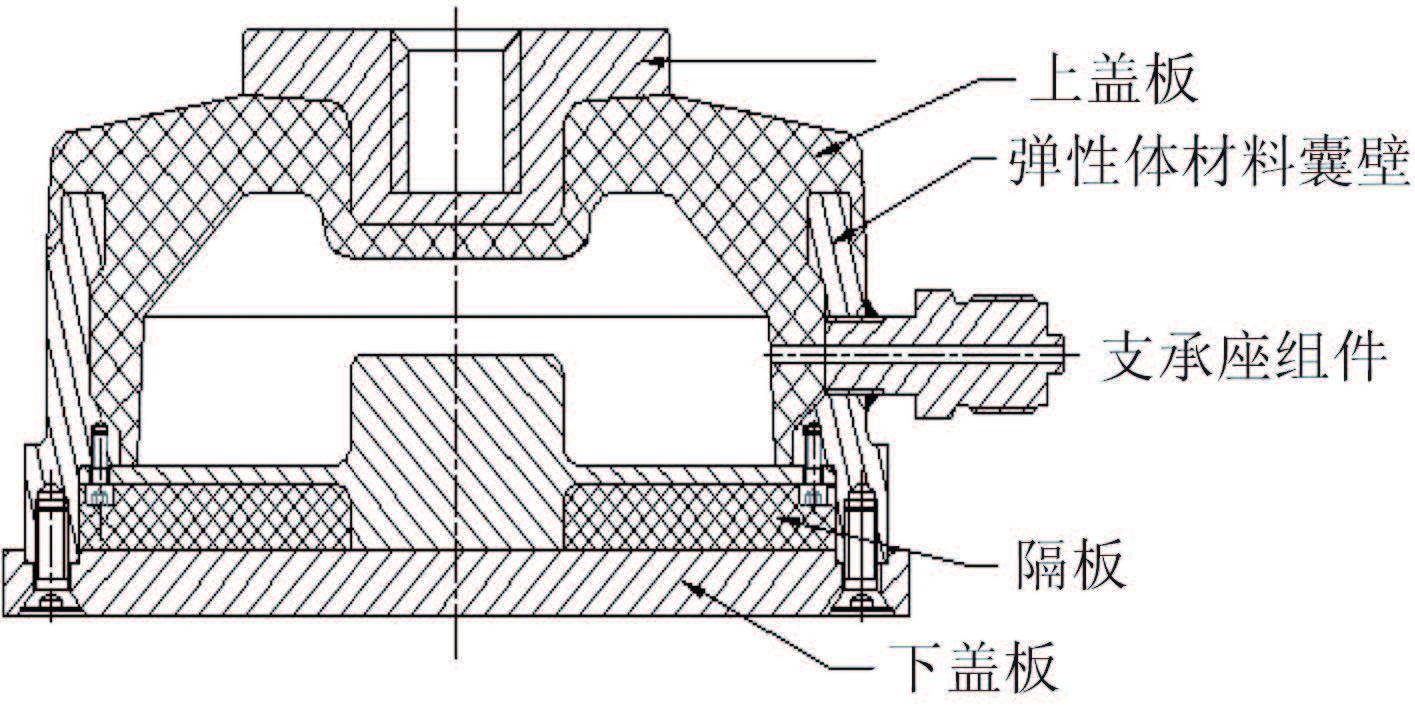
本文将研究一种复合式气囊隔振器,其结构和实物如图 1 和图 2 所示,这种隔振器由上盖板、支承座组件、隔板、下盖板和弹性体囊壁所构成,隔板起到了密封作用,金属件和弹性体硫化粘结在一起。在充气或不充气的情况下,这种复合式气囊隔振器都可以工作。
|
图 1 复合式气囊隔振器结构图 Fig. 1 Schematic diagram of the complex air spring |

|
图 2 复合式气囊隔振器实物图 Fig. 2 Complex air spring |
本文将研究这种隔振器垂向静态特性的计算方法,并用有限元计算和实验方法验证计算方法的正确性。
1 垂向静态特性计算研究这种隔振器的垂向刚度由弹性体囊壁和气囊两部分构成,由于气囊上盖板移动时,弹性体囊壁和气囊在垂向共位移[4],即轴向位移量相同,所以弹性体囊壁和气囊是并联的关系,隔振器的垂向静刚度为
| $k = {k_k} + {k_t}.$ | (1) |
式中:kk 为气囊的静刚度;kt 为弹性体囊壁的静刚度。因此隔振器的刚度可以分解为囊壁刚度和气囊刚度两部分进行研究。
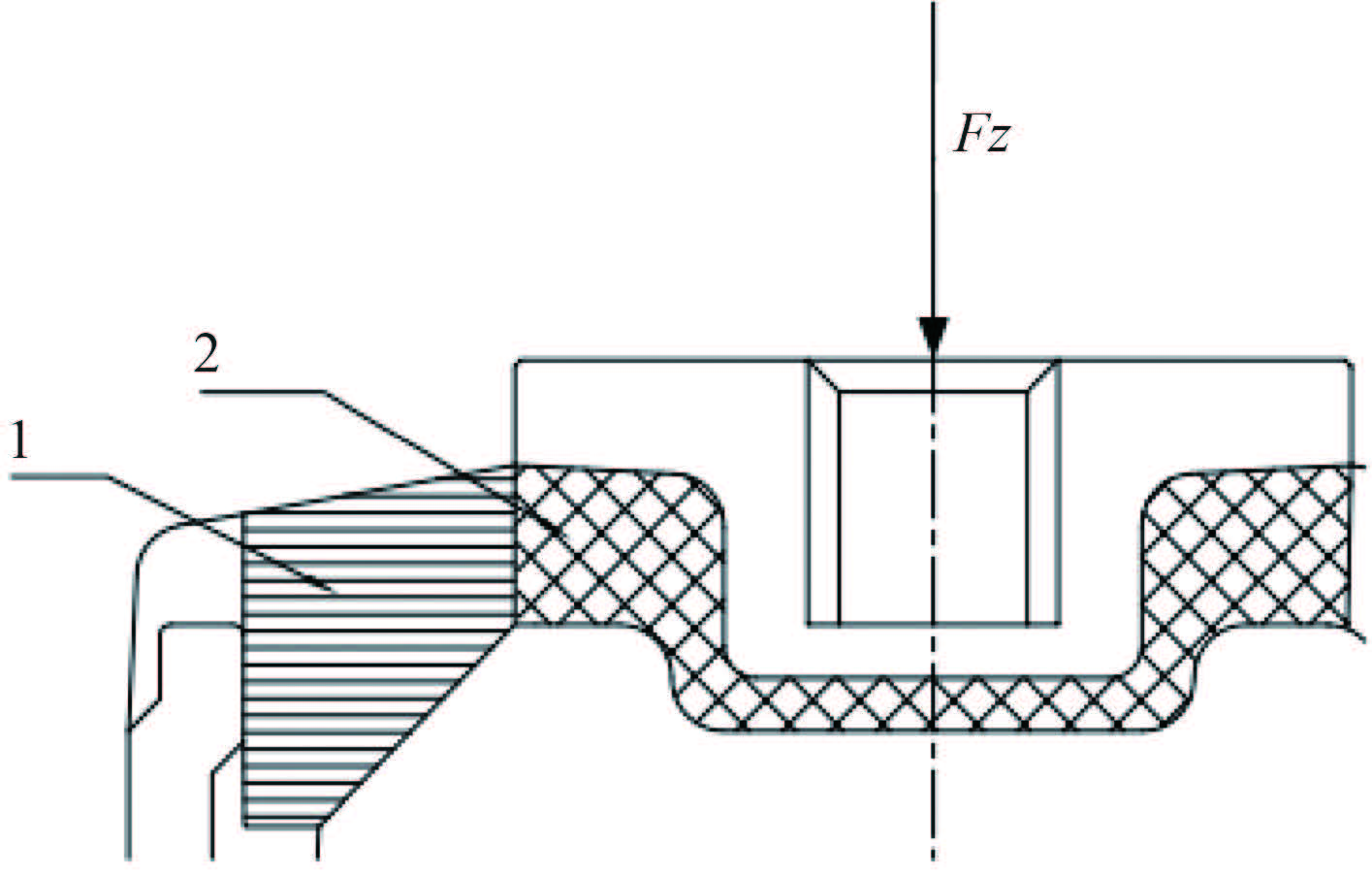
1.1 弹性体囊壁的垂向静刚度计算如图 3 所示,上盖板与弹性体 2 硫化粘结在一起,且由弹性体材料的近似不可压缩性可知,当弹性体囊壁受到垂向力 FZ 时,盖板和弹性体 2 会整体下移,弹性体 2 几乎不会发生形变,可以将弹性体 2 假定属于盖板,这样弹性体 2 和弹性体 1 可以看作是粘合在一起的两部分,当弹性体囊壁受到垂向力 FZ 时,隔振器受力部分为弹性体 1。
|
图 3 隔振器局部图 Fig. 3 A part of complex air spring |
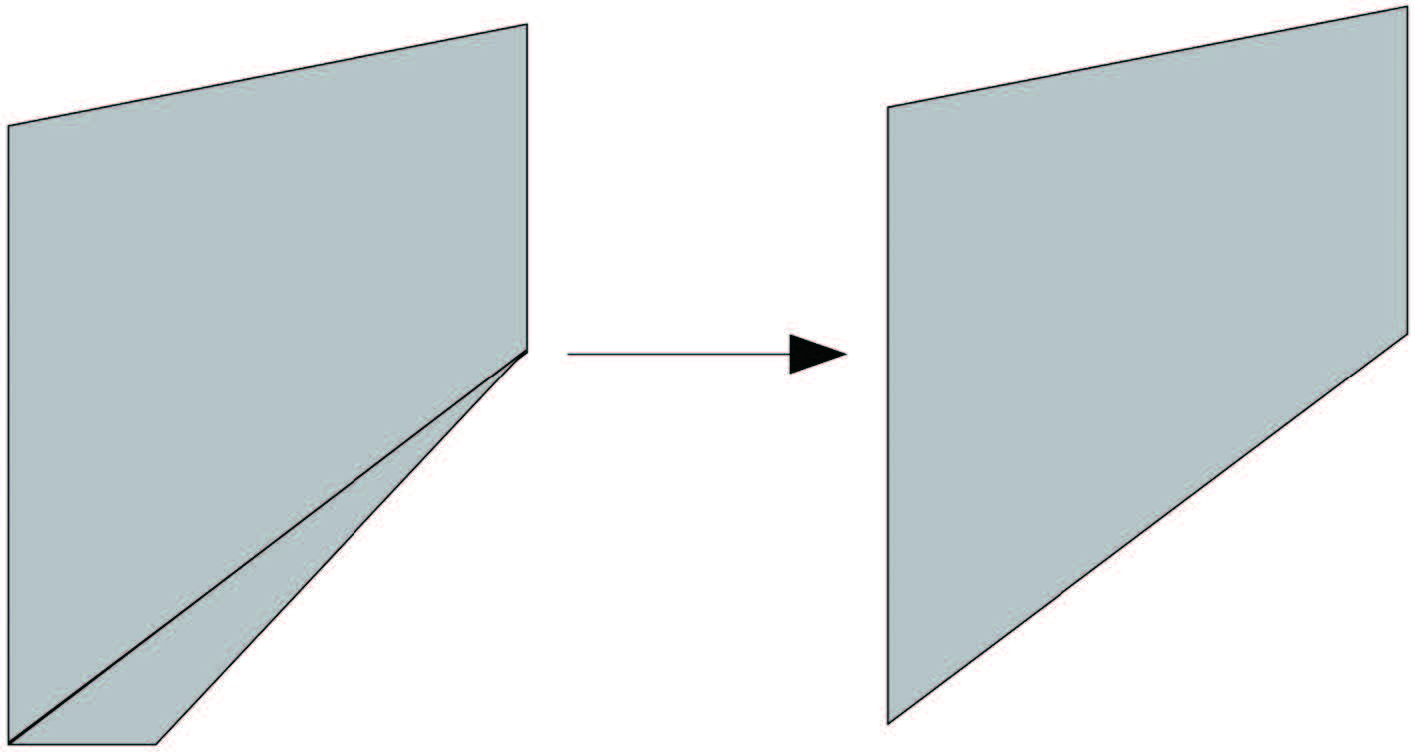
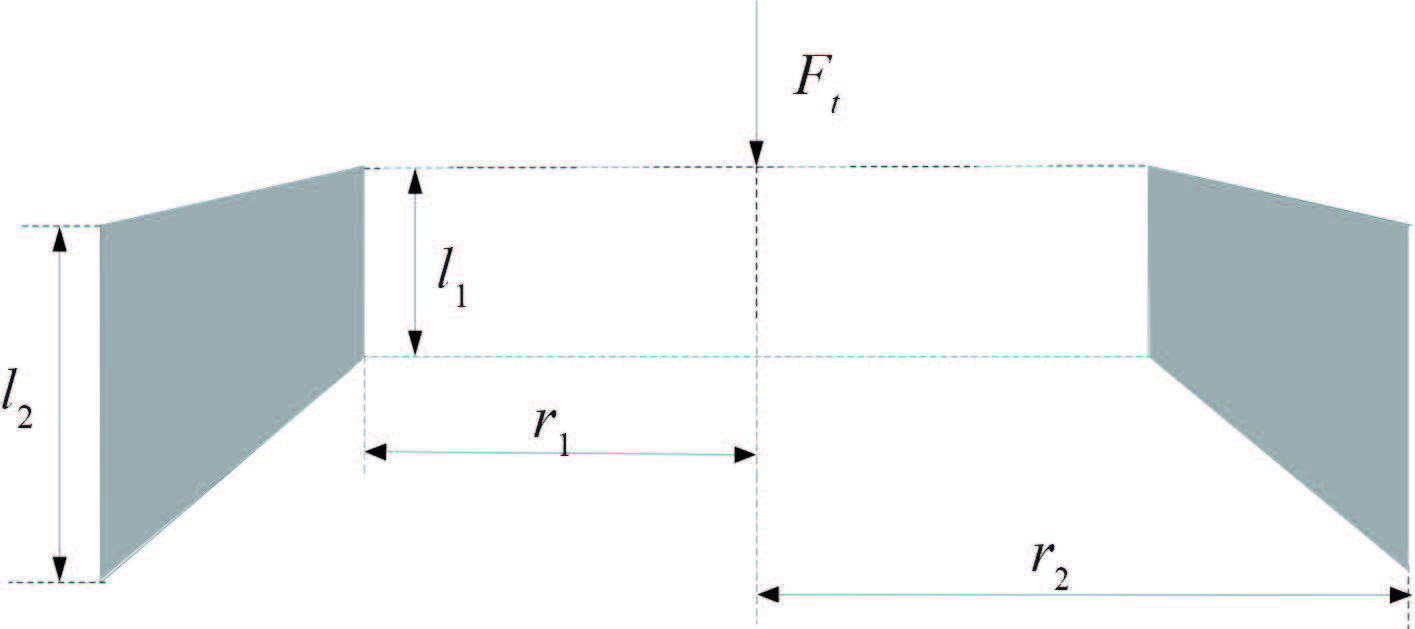
为简化计算可将弹性体 1 做如图 4 所示的简化,所省去的弹性体较小,对计算影响不大,于是可得到如图 5 所示的计算模型。这种弹性体的受力为剪切型,根据剪切型隔振器垂向刚度的计算公式可得弹性体的垂向静刚度为[5]
| ${k_t} = \frac{{2{G_{ap}}({l_2}{r_1} - {l_1}{r_2})}}{{({r_2} - {r_1}){\rm{ln}}\frac{{{l_2}{r_1}}}{{{l_1}{r_2}}}}}.$ | (2) |
|
图 4 弹性体受力部分简化图 Fig. 4 The simplified diagram of elastic body on load |
|
图 5 弹性体计算模型 Fig. 5 Calculation model of elastic body |
其中 Gap 为弹性体的表观剪切模量。
对于同一种材料不同结构的隔振器而言,虽然隔振器弹性部件的物理性能不会由于外表形状而改变,但隔振器的结构形状却会影响隔振器的刚度性能[6]。因此,对于确定结构的隔振器,弹性体的剪切模量不再是 G,而是表观剪切模量 Gap,两者的关系为
| ${G_{ap}} = m \times G.$ | (3) |
式中 m 为形状系数,本文研究的这种弹性体的形状系数可按如下公式计算[7]
| $m = 1 + \frac{1}{3}\frac{{{{({r_2} - {r_1})}^2}}}{{{l_1}{l_2}}}.$ | (4) |
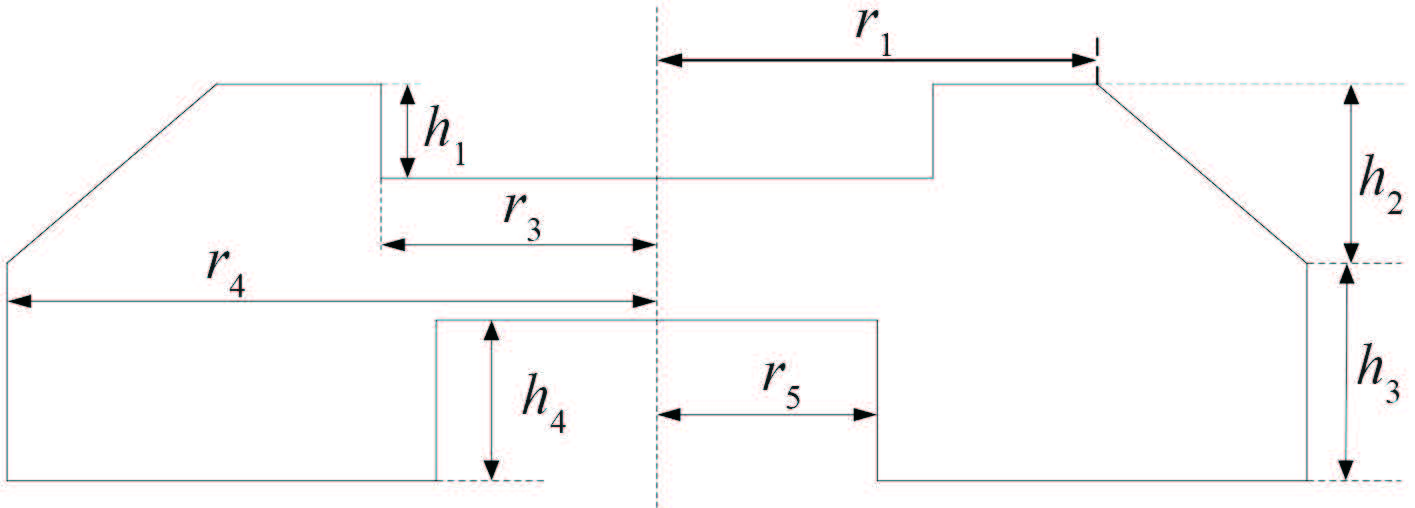
气囊的计算模型如图 6 所示。
|
图 6 气囊的计算模型 Fig. 6 Calculation model of air cavity |
气囊的轴向反力可用下面的公式来表示:
| ${F_k} = P{A_{eff}}.$ | (5) |
式中:P 为内部气体表压;Aeff 为气囊的有效面积。
如果在负载的作用下,隔振器盖板产生一个很小的位移 dZ,则负载对气囊做的功为 FkdZ,而压力的功为 PdV,不考虑能量的损耗,根据虚位移原理可以得到
| ${F_k}dZ + P{\rm{d}}V = 0.$ | (6) |
结合式(5)可得到
| ${A_{eff}} = \frac{{{F_k}}}{P} = - \frac{{{\rm{d}}V}}{{{\rm{d}}Z}}{\rm{.}}$ | (7) |
其中 V 为气囊的容积。
由气囊的结构图可以看出气囊的初始容积为
| ${V_0} = \frac{\pi }{3}{h_2}(r_4^2 + r_1^2 + {r_1}{r_4}) - \pi r_3^2{h_1} + \pi r_4^2{h_3} - \pi r_5^2{h_4}.$ | (8) |
当隔振器上盖板向下移动 Z 的距离时,气囊随之被压缩,h2 减小 Z 的距离,则气囊的容积为
| $V = \frac{{\pi ({h_2} - Z)}}{3}(r_4^2 + r_1^2 + {r_1}{r_4}) - \pi r_3^2{h_1} + \pi r_4^2{h_3} - \pi r_5^2{h_4}.$ | (9) |
将式(9)代入式(7)可得
| ${A_{eff}} = \frac{\pi }{3}(r_4^2 + r_1^2 + {r_1}{r_4}).$ | (10) |
根据理想气体热力学方程,对于气囊内部的封闭气体有
| $(P + {P_a}){V^n} = ({P_0} + {P_a})V_0^n{\rm{.}}$ | (11) |
式中:P,V 分别为气囊气体表压和容积;P0,V0 分别为表压和体积的初始状态值;Pa 为大气压力;n 为气体多变指数,其值取决于气囊隔振器变形的速度。当气囊的振动频率 $f < 0.2$ Hz时,气体的变化过程可视为等温过程,$n \approx 1$;当 $f \geqslant 0.2$ Hz时,气体变化过程可视为绝热过程,$n \approx $1.3 ~ 1.4。
所以气囊的内部气压、气囊轴向反力为
| $P = ({P_0} + {P_a}){(\frac{{{V_0}}}{V})^n} - {P_a}{\rm{.}}$ | (12) |
| ${F_k} = P(Z){A_{eff}}(Z).$ | (13) |
气囊的垂向刚度为
| ${k_k} = \frac{{{\rm{d}}{F_k}}}{{{\rm{d}}Z}} = n\frac{{(P + {P_a})}}{V}{A_{eff}}^2{\rm{.}}$ | (14) |
本文研究的静态特性可视作等温过程,n 取 1。
1.3 隔振器的垂向静刚度由以上的研究可得该型隔振器在不充气情况下的垂向静刚度为
| $k = {k_t} = \frac{{2\pi {G_{ap}}({l_2}{r_1} - {l_1}{r_2})}}{{({r_2} - {r_1}){\rm{ln}}\frac{{{l_2}{r_1}}}{{{l_1}{r_2}}}}}.$ | (15) |
在充气情况下的垂向静刚度为
| $k = {k_t} = \frac{{2\pi {G_{ap}}({l_2}{r_1} - {l_1}{r_2})}}{{({r_2} - {r_1}){\rm{ln}}\frac{{{l_2}{r_1}}}{{{l_1}{r_2}}}}}{\rm{.}}$ | (16) |
本文所研究的复合式气囊隔振器的弹性体囊壁采用聚氨酯材料,其剪切模量为 2.88 MPa,结构尺寸如表 1 所示。
|
|
表 1 复合式气囊隔振器结构尺寸 Tab.1 Structure dimension of complex air spring |
计算隔振器在不充气和充气 0.51 MPa 时的垂向静刚度,经计算在不充气时的垂向静刚度为 533 N/mm,在充气 0.51 MPa 时的垂向静刚度为 646 N/mm。
2 仿真分析 2.1 隔振器聚氨酯弹性体材料特性在 Marc 有限元软件中对橡胶类材料的处理有多种本构模型,较为常见的有:Mooney-Rivilin 模型,Ogden 模型。对于聚氨酯材料使用 Ogden 模型进行材料模拟较为准确 Ogden 应变能密度函数的表达式为[8]
| $W = \sum\limits_{i = 1}^N {\frac{{{\mu _i}}}{{{\alpha _i}}}} \left( {\lambda _1^{{\alpha _i}} + \lambda _2^{{\alpha _i}} + \lambda _3^{{\alpha _i}}} \right) + \sum\limits_{i = 1}^N {\frac{1}{{{D_i}}}} {\left( {J - 1 - R} \right)^i}.$ | (17) |
其中 αi,μi,Di 和 R 同温度有关,可以看作是材料参数,数值由试验确定;J=λ1λ2λ3,为变形后与变形前的体积比,幂指数 αi 是能拟合完全非线性试验数据的任意实数。
将聚氨酯单轴拉伸的名义应变 - 名义应力数据输入到 Marc 的材料拟合功能模块中,得到聚氨酯材料在 Ogden 模型下的材料参数,并用拟合的材料常数定义隔振器模型的聚氨酯材料。
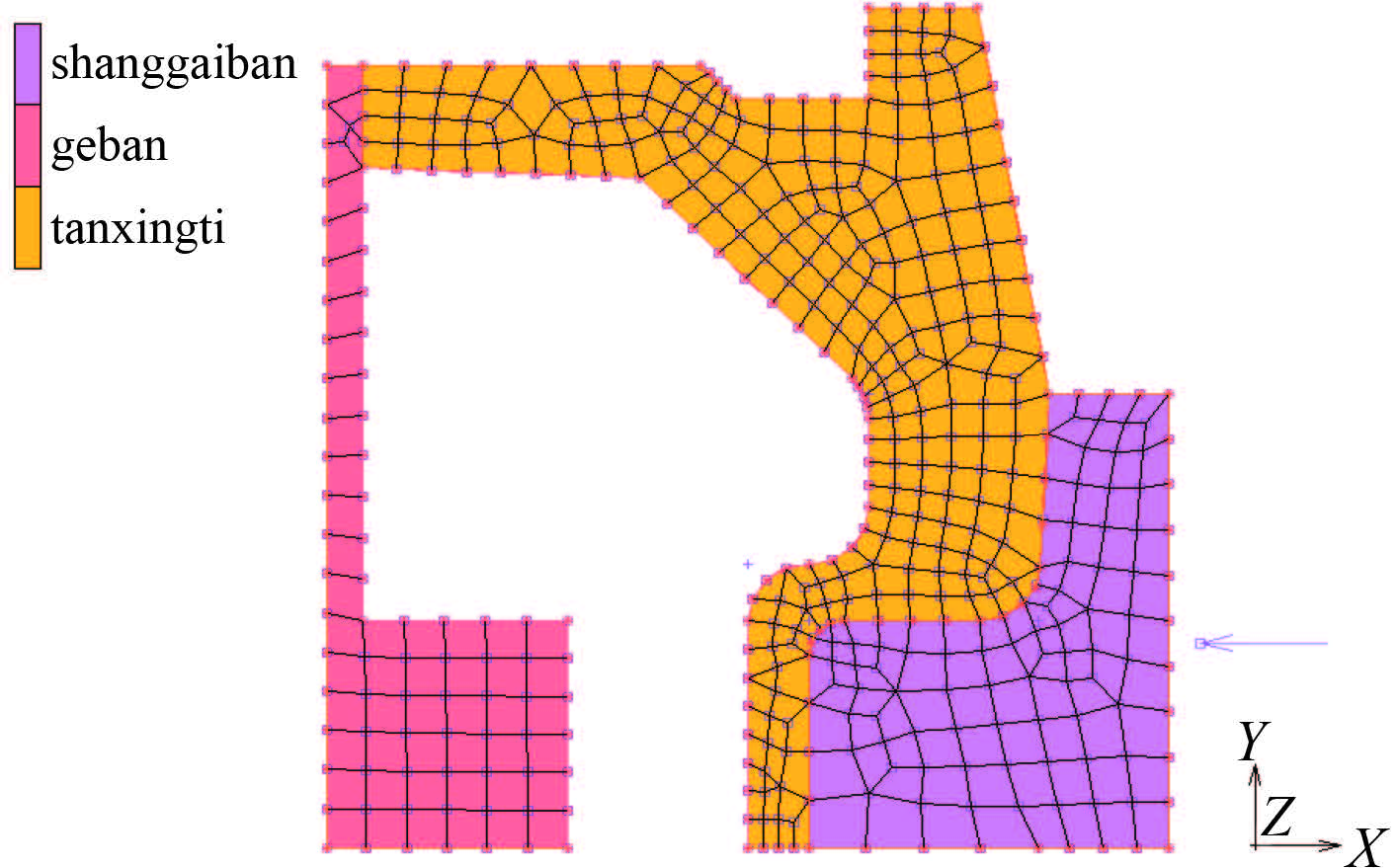
2.2 有限元模型建立本文分析研究的复合式气囊隔振器具有轴对称性以及垂向力的轴对称性,对于垂向特性的计算,可取隔振器的一个轴对称面作为计算模型进行轴对称分析。隔振器发生垂向位移时,气囊容积会发生变化,因此气压将发生变化,需要对气体进行适当的模拟。非线性有限元软件 Marc 中的 Cavity 单元,可以通过施加 Mass 和 Press 载荷模拟气体的变化。在垂向特性计算时,为方便对上盖板进行位移约束,在上盖板上设置刚性线和控制点,在仿真计算时对上盖板做 X 向位移,通过求得垂向力来获得垂向特性。隔振器离散后有节点 486 个,单元 375 个离散模型如 图 7 所示。
|
图 7 隔振器的有限元模型 Fig. 7 Finite element model of air spring |
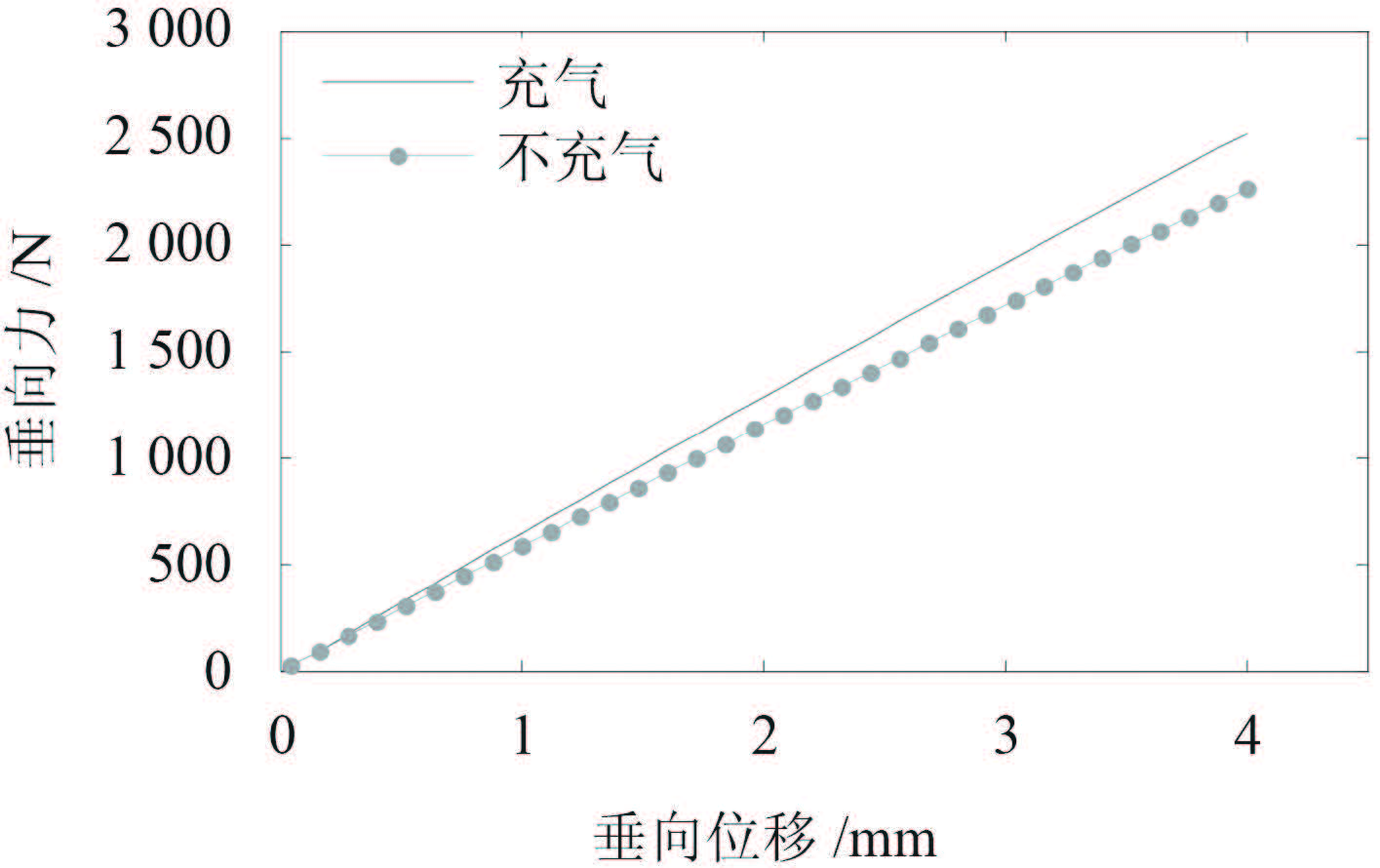
有限元计算的垂向静态特性如图 8 所示,经计算隔振器在不充气时的垂向静刚度为 565 N/mm,在充气压力为 0.51 MPa 时的垂向静刚度为 626 N/mm。
|
图 8 垂向静态特性有限元计算结果 Fig. 8 Vertical static properties of finite element analysis |
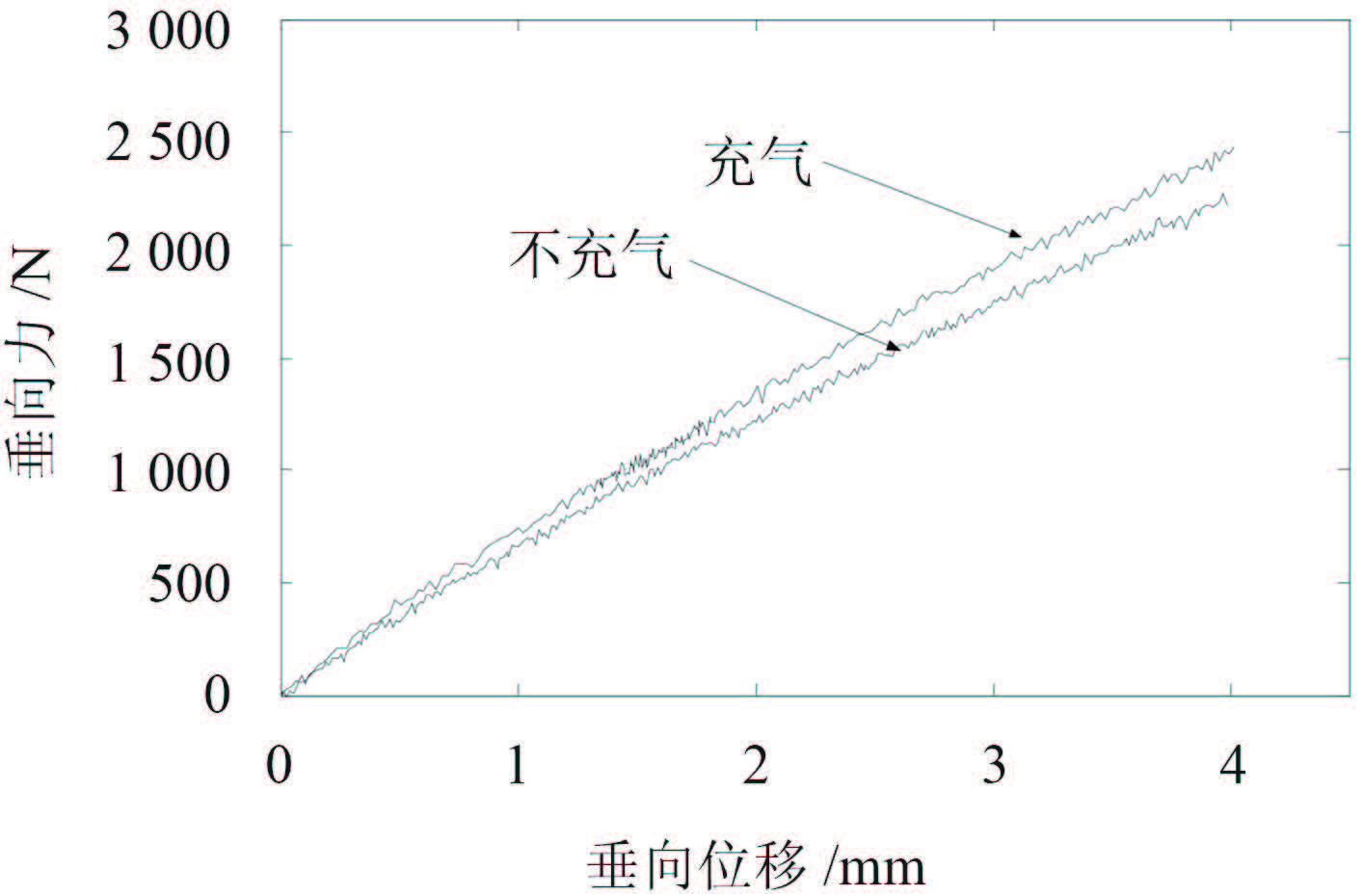
为验证隔振器静态特性计算方法的有效性,在 MTS 810 型通用液压伺服试验机上对复合式气囊隔振器进行了不充气和充气 0.51 MPa 下的垂向静态特性的实验,由实验结果求得在不充气时的静刚度为 543 N/mm,在充气 0.51 MPa 时的静刚度为 608 N/mm。实验结果如图 9 所示。
|
图 9 垂向静态特性实验结果 Fig. 9 Vertical static properties of experimental measurement |
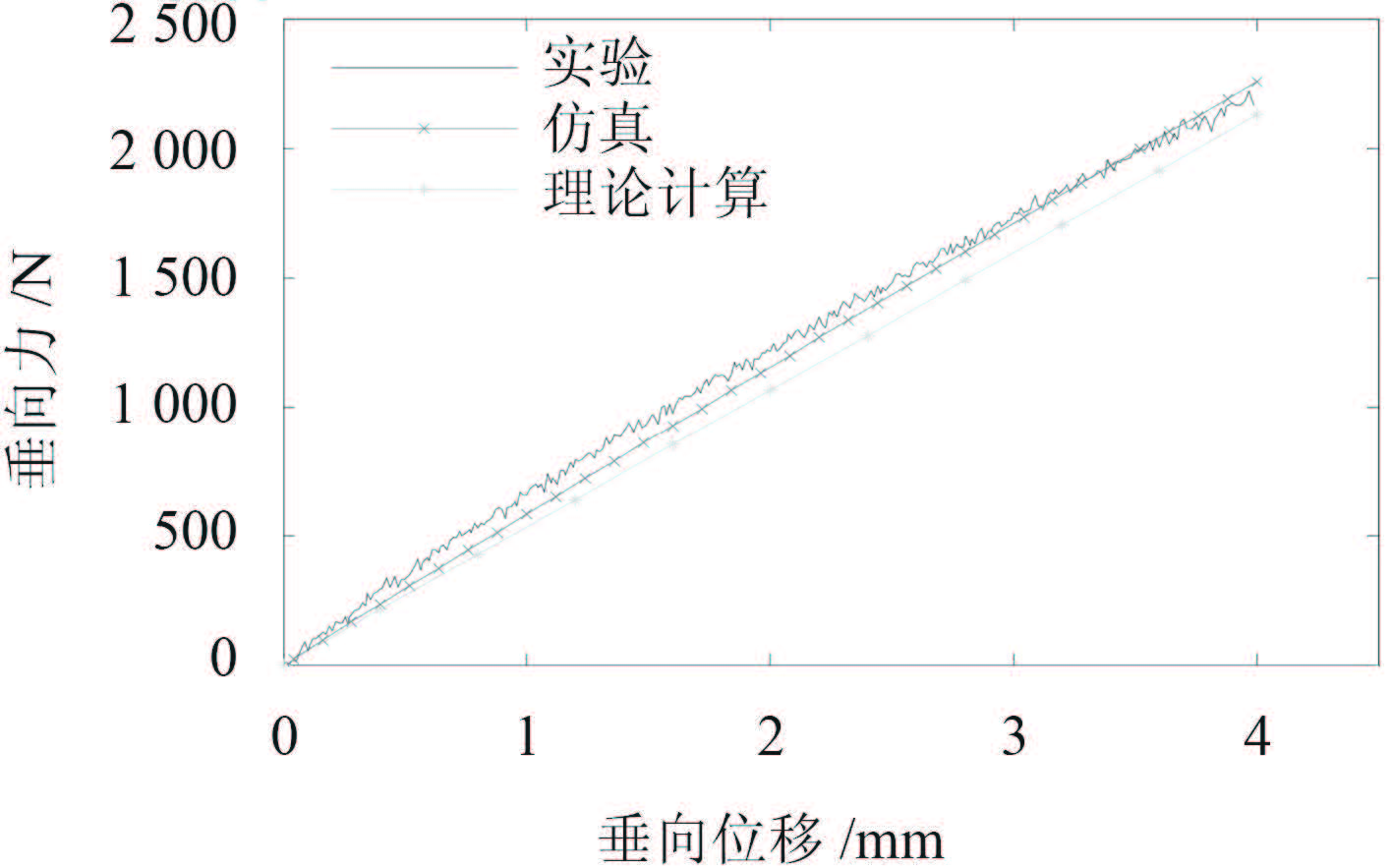
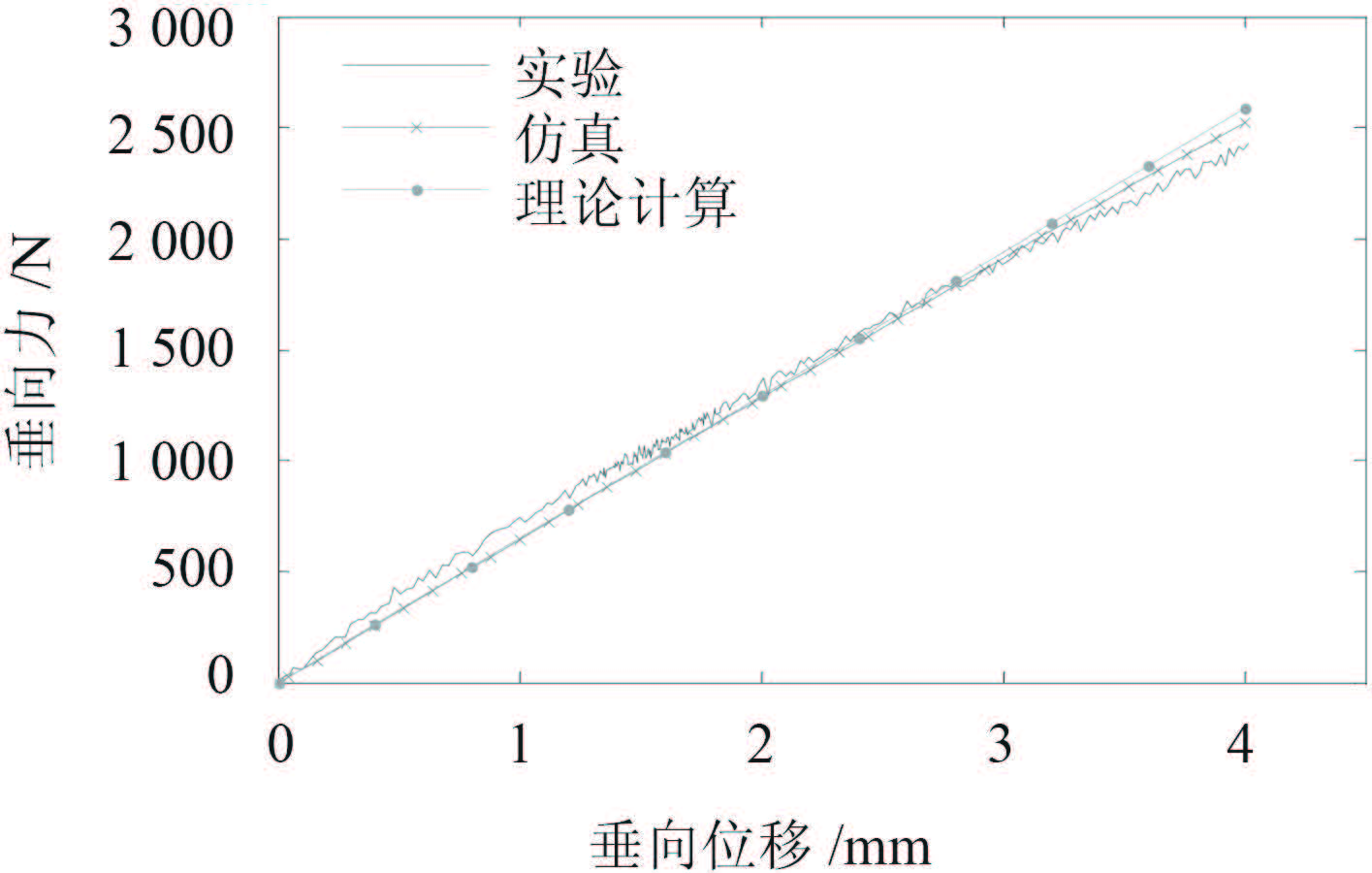
静态特性计算和仿真、实验结果对比如图 10 ~ 图 11 所示。将理论计算和仿真计算结果分别和实验结果作比较,并得到其相对误差,其结果见表 2。
|
图 10 不充气时隔振器垂向静态特性 Fig. 10 Vertical static properties of complex air spring in not inflation situation |
|
图 11 充气时隔振器垂向静态特性 Fig. 11 Vertical static properties of complex air spring in inflation situation |
|
|
表 2 隔振器垂向静刚比较 Tab.2 Comparisonof vertical static properties of air spring |
理论计算与仿真计算、实验测得的静刚度的相对误差都在 10% 以内。
图 10 和图 11 的结果分析说明,本文所研究的复合式气囊隔振器垂向静态特性的计算方法有效,可以用于该类隔振器垂向静态特性的计算。
5 结 语本文通过理论计算和有限元仿真的方法研究了复合式气囊隔振器的垂向静态特性,并与实验结果进行比较,得到以下结论:
1)轴系横向振动模态频率对轴承刚度、基座刚度存在敏感区,轴系设计时可根据模态频率对刚度的敏感情况适当调整轴承刚度和基座刚度;
2)轴系横向振动存在的部分稳定模态频率,不随轴承刚度、基座刚度变化,若该阶模态频率为振动控制对象,改变轴系支撑刚度难以达到优化模态频率的控制目标;
3)对于 4#轴承,强基座刚度、弱轴承刚度,有利于降低螺旋桨横向激励力通过轴系向 4#轴承的传递;
4)对于舱内油润滑轴承,轴承刚度、基座刚度改变对螺旋桨激励通过轴系向 4#轴承的传递影响较小,轴系横向振动控制设计时可忽略。
| [1] | 朱石坚, 何琳. 船舶减振降噪技术与工程设计[M]. 北京: 科学出版社, 2002 . |
| [2] |
赵应龙, 吕志强, 何琳. JYQN舰用气囊隔振器研究[J]. 舰船科学技术 , 2006, 28 (S2) :89–92.
ZHAO Ying-long, LV Zhi-qiang, HE Lin. Study of pneumatic vibration isolator of type JYQN[J]. Ship Science and Technology , 2006, 28 (S2) :89–92. |
| [3] |
吴恒亮, 代会军. 橡胶隔振器设计开发研究[J]. 噪声与振动控制 , 2009, 29 (1) :114–116.
WU Heng-liang, DAI Hui-jun. Application of finite element analysis in design and development of rubber isolators[J]. Noise and Vibration Control , 2009, 29 (1) :114–116. |
| [4] | 师汉民, 黄其柏. 机械振动系统[M].版本. 武汉: 华中科技大学出版社, 2013 . |
| [5] | 严济宽. 机械振动隔离技术[M]. 上海: 上海科学技术文献出版社, 1985 . |
| [6] | 刘柏峰. 聚氨酯隔振器性能分析与试验研究[D]. 武汉:海军工程大学, 2010. |
| [7] | 户原春彦. 防振橡胶及其应用[M]. 北京: 中国铁道出版社, 1982 . |
| [8] | OGDEN R W. Non-linear elastic deformations[M]. Chichester, UK: Ellis Horwood, 1984 . |
 2016, Vol. 38
2016, Vol. 38
