水下航行器的空间运动本质上是刚体的三维空间运动。结构合理、性能优良的操纵装置将极大地影响航行器的运动特性。分离式尾升降舵的左、右舵由各自的液缸驱动,两舵可按各自的指令转动。当一舷尾升降舵发生事故后,在采取降速、操纵首升降舵等挽回措施的同时,可以操纵另一舷的尾升降舵进行挽回。同时在正常航行时,可以用分离式尾升降舵的左、右舵转差动舵角,产生横倾力矩,对航行器的横倾进行控制。首升降舵安装在航行器的的首部,可有效改善水下航行器的操纵性能,减少高速航行的水下航行器噪声。
本文针对高维多输入具有强非线性且高度耦合的分离式尾舵和收放式首舵水下航行器操纵控制系统,研究基于非线性鲁棒滑模控制方法的自动操纵控制方案。在水下航行器六自由度空间运动方程[1]基础之上,提出非线性鲁棒滑模控制算法。将所设计的滑模控制器与水下航行器动态相连接,构成闭环系统,数值仿真结果验证所提出的算法可以有效解决分离式尾舵且首舵收回状态下的水下航行器的操纵控制问题。
1 分离式尾舵水下航行器在首舵收回时的数学模型水下航行器水下运动是多姿态的三维空间运动,对分离式尾舵收放式首舵操纵控制技术进行研究,通过计算机仿真要对其进行比较准确的描述和对运动状态及控制效果进行动态仿真研究,其关键技术是建立仿真数学模型。
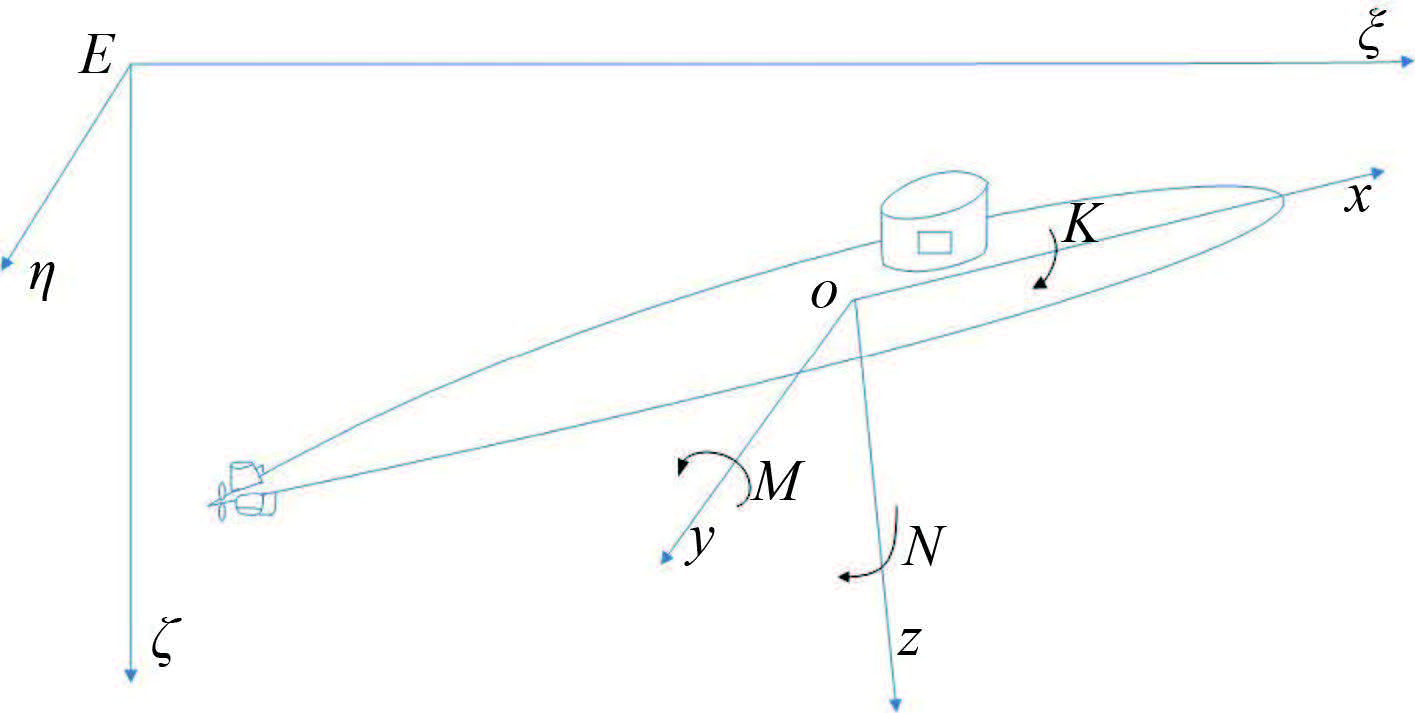
为完整地描述水下航行器的动力学与运动学特性,需要建立定系和动系 2 个坐标系。定系 E-ξηζ 是坐标系原点固定于水面上或水中某一定点的右手直面坐标系。Eζ 轴正向指向地心,Eξ 和 Eη 轴在同一水平面内,Eξ 轴正向为水下航行器的基准方向,Eη 轴正向按右手系确定;动系 o-xyz 是固定于水下航行器上的右手直角坐标系。xoz 平面与中纵剖面相重合,xoy 平面与基面相平行,yoz 平面与中横剖面平行。ox 轴向船首为正,oz 轴向下为正,oy 轴向以右舷为正。上述关系如图 1 和图 2 所示。
|
图 1 固定坐标系和随船坐标系 Fig. 1 The fixed coordinate system and ship coordinate system |
|
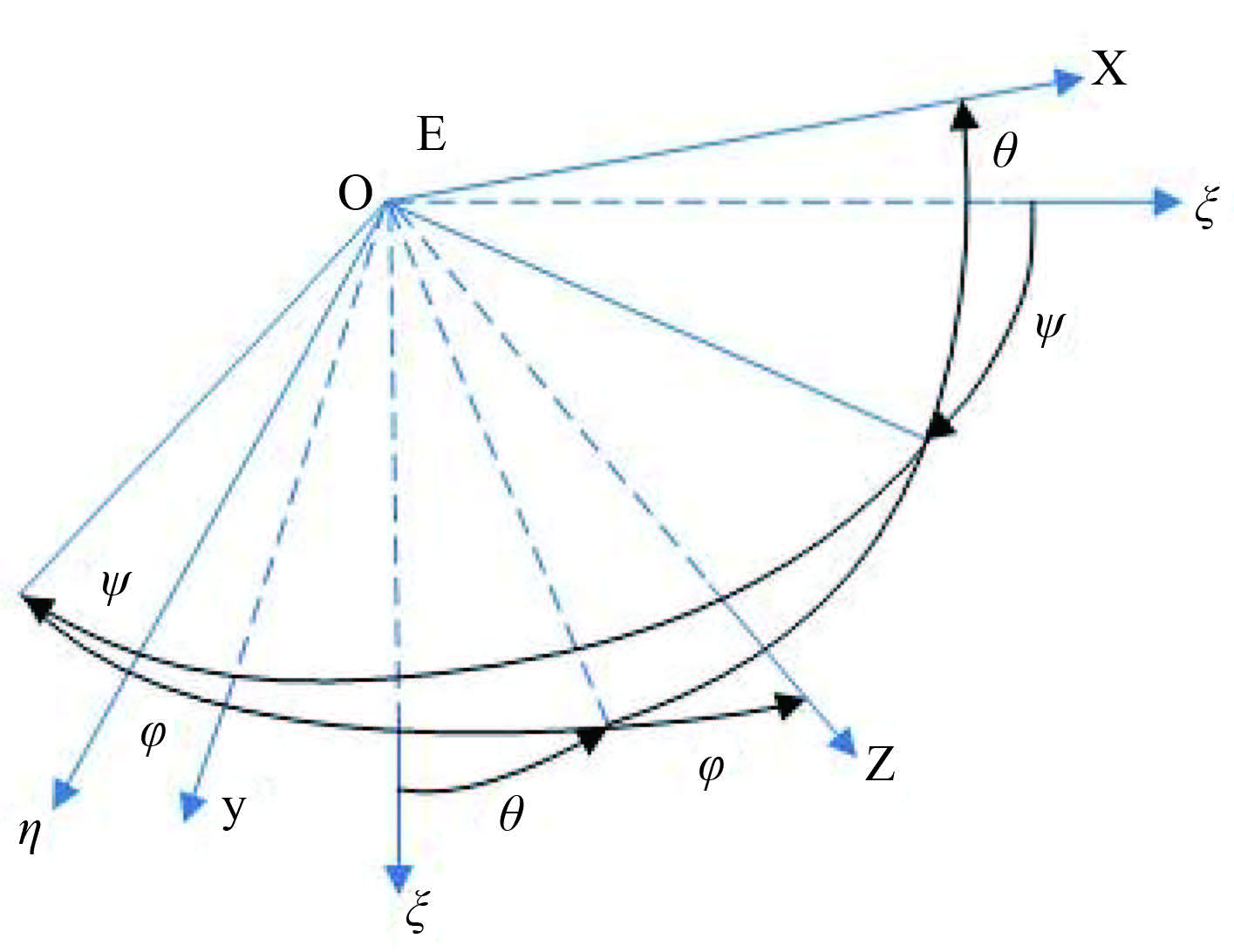
图 2 欧拉角 Fig. 2 Euler angles |
水下航行器的空间位置和姿态由动系原点在定系中的坐标值[ξ0,η0,ζ0]T 和动系相对于定系的 3 个欧拉角 ξ2 = [φ,θ,ψ]T 来描述。φ,θ,ψ 分别为水下航行器的横倾角、纵倾角和偏航角。
因此水下航行器在水中的六自由度的一般运动由状态向量 ${{x}} = {[{{{x}}_1}^{\text{T}},{{{x}}_2}^{\text{T}}]^{\text{T}}}$ 来描述:${{{x}}_1} = {[u,v,w,p,q,r]^{\text{T}}}$,x1 中各量分别为水下航行器的纵向速度、横向速度、垂向速度、横倾角速度、纵倾角速度和回转角速度;${{{x}}_{\bf{2}}} = {[\varphi ,\theta ,\psi ,{\xi _o},{\eta _o},{\zeta _o}]^{\text{T}}}$,x2 中各量分别为水下航行器的横倾角、纵倾角、首向角以及在定系中的位置坐标。
由上可知,x1 描述了水下航行器相对于动系的平动速度和旋转速度,而 x2 则描述了其相对于定系的位置和姿态。
水下航行器在动系和定系的平动速度之间存在如下的坐标变换 T1:
| $\frac{\text{d}}{\text{d}t}{{[{{\xi }_{o}},{{\eta }_{o}},{{\zeta }_{o}}]}^{\text{T}}}={{T}_{1}}\left[ \begin{matrix} u \\ v \\ w \\ \end{matrix} \right],$ |
其中
| ${{T}_{1}}={{T}_{1}}(\varphi ,\theta ,\psi )=\left[ \begin{matrix} \cos \psi \cos \theta & -\sin \psi \cos \varphi +\cos \psi \sin \theta \sin \varphi & \sin \psi \sin \varphi +\cos \psi \sin \theta \cos \varphi \\ \sin \psi \cos \theta & \cos \psi \cos \varphi +\sin \psi \sin \theta \sin \varphi & -\cos \psi \sin \theta +\sin \psi \sin \theta \cos \theta \\ -\sin \theta & \cos \theta \sin \varphi & \cos \theta \cos \varphi \\ \end{matrix} \right],$ |
注意到 T1-1 = T1T,故 T1 正交。
水下航行器在动系和定系中的旋转速度之间有如下坐标变换 T2:
| $\frac{\text{d}}{\text{d}t}{{[\varphi ,\theta ,\psi ]}^{\text{T}}}={{T}_{2}}\left[ \begin{matrix} p \\ q \\ r \\ \end{matrix} \right],$ |
其中
| ${{T}_{2}}=\left[ \begin{matrix} 1 & \sin \varphi \tan \theta & \cos \varphi \tan \theta \\ 0 & \cos \varphi & -\sin \varphi \\ 0 & \frac{\sin \varphi }{\cos \theta } & \frac{\cos \varphi }{\cos \theta } \\ \end{matrix} \right]\circ $ |
若要使 T2 有界,需要有 ${\text{|}}\theta {\text{| < }}\frac{\pi }{{\text{2}}}$,且 T2-1 ≠ T2T,因此 T2 不正交。
本论文使用的运动仿真数学模型见参考文献[1]中潜艇六自由度空间运动方程。
水下航行器运动关系式如下:
| $\begin{aligned} & {{U}^{2}}={{u}^{2}}+{{w}^{2}}+{{v}^{2}}\text{,} \\ & {{{\dot{\xi }}}_{0}}=u\cos \psi \cos \theta +v(\cos \psi \sin \theta \sin \phi -\sin \psi \cos \phi )+ \\ & \quad \quad w(\cos \psi \sin \theta \cos \phi +\sin \psi \sin \phi )\text{,} \\ & {{{\dot{\eta }}}_{0}}=u\sin \psi \cos \theta +v(\sin \psi \sin \theta \sin \phi +\cos \psi \cos \phi )+ \\ & \quad \quad w(\sin \psi \sin \theta \cos \phi -\cos \psi \sin \phi )\text{,} \\ & {{{\dot{\zeta }}}_{0}}=-u\sin \theta +v\cos \theta \sin \phi +w\cos \theta \cos \phi \text{,} \\ & \dot{\phi }=p+q\tan \theta \sin \phi +r\tan \theta \cos \phi \text{,} \\ \end{aligned}$ |
| $\begin{aligned} & \dot{\theta }=q\cos \phi -r\sin \phi \text{,} \qquad\qquad\qquad\qquad\quad\\ & \dot{\psi }={}^{\displaystyle(q\sin \phi +r\cos \phi )}\!\!\diagup\!\!{}_{\cos \theta }\; \text{,}\qquad\qquad\qquad\qquad\quad\\ \end{aligned}$ |
在本研究中将上述围壳舵水下航行器动力学模型中的首舵舵角恒设为 0,以此表述首舵收回时的水下航行器动态。尽管首舵设定为 0 和首舵完全收回时的动态有差异,而该影响会反映在水下航行器的其他水动力系数的相应改变上,然而这种水动力系数值的变化不大,影响较小,因此将首舵舵角恒设为 0 的近似处理方式合理。本研究中的仿真和控制器设计均基于该假设。
2 非线性鲁棒滑模控制算法水下航行器在水下的空间运动具有 6 个自由度,包括沿轴向的 3 个线位移和绕轴的 3 个角位移。可以通过方向舵、首尾升降舵、均衡水箱和发动机等设备来实施水下航行器操纵。但每种操纵动作都会对水下航行器运动的各个自由度产生不同程度的影响,水下航行器将产生明显的升沉运动,严重影响水下航行器的战斗使命。滑模控制方法的优点在于可以采用不准确的数学模型,可以计入不确定干扰作用的影响,同时还可以用来消除非线性和耦合的影响。因此用滑模控制方法来设计水下航行器定深定向运动状态下的运动控制器较为合适。
基于系统的状态变量定义系统的滑模面如下:
| $C £ \tilde x = C\tilde x.$ |
式中:$\tilde x = x - {x_d}$ 为状态跟踪误差;C 为由已知系数构成的合适维数的矩阵。
对于滑模面的定义来说,必须保证:当 $\sigma(\tilde x)\to 0$ 时有状态跟踪误差 $\tilde x \to 0$。
水下航行器功能子系统的动态模型可描述为:
| $\dot{x}=Ax+{{B}_{{}}}{{u}_{{}}}+\delta f\circ $ |
其中 δf 应该解释为一个非线性函数,它刻画了子系统的外干扰与未建模动态。那么反馈控制算法将包含 2 个部分:
| $u=\hat{u}+\bar{u},$ |
其中名义控制部分为
| $\hat{u}=-Kx\circ $ |
这里的 K 为反馈增益矩阵。
将上述表达式代入系统动态方程得到闭环动态为:
| $\begin{align} & \dot{x}={{A}_{c}}x+B\bar{u}+\delta f, \\ & {{A}_{c}}=A-BK\circ \\ \end{align}$ |
因此反馈增益矩阵 K 可以通过极点配置方法来确定。
经推导非线性鲁棒滑模控制算法为:
| $u=\hat{u}+\bar{u}=-Kx+{{(CB)}^{-1}}[C{{\dot{x}}_{d}}-C\delta \hat{f}-\eta \text{sgn}(\sigma )]$ |
其中 C 为滑模面的系数矩阵。
为消除上面所示的滑模控制算法的抖动,引入边界层控制。将上式中的符号函数 sgn(δ)替换为具有滑模面边界层厚度 φ 的双曲正切函数 $\tan h(\frac{\sigma }{\varphi })$。
因此引入边界层厚度 φ 的非线性鲁棒滑模控制算法为:
| $\begin{array}{l} u = \hat u + \bar u= - { K}x + {({ CB})^{ - 1}}[{ C}{{\dot x}_d} -{ C} \delta \hat f - \eta \tanh (\frac{\sigma }{\phi })] \end{array}$ |
综上所述,非线性鲁棒滑模控制算法为:
| $u=\left\{ \begin{array}{*{35}{l}} -Kx+{{(CB)}^{-1}}[C{{{\dot{x}}}_{d}}-C\delta \hat{f}-\eta \text{sgn}(\sigma )] \\ \text{discontinuousversion}, \\ -Kx+{{(CB)}^{-1}}[C{{{\dot{x}}}_{d}}-C\delta \hat{f}-\eta \tanh (\frac{\sigma }{\varphi })] \\ \text{continuousversion} \\ \end{array} \right.$ |
由于滑模控制器设计时对系统的数学模型要求比较宽松,也就是说对系统摄动或外部干扰的要求并不苛刻,这样在水下航行器运动控制系统设计时模型的处理就方便多了,特别是各耦合项和非线性项均可以归入不可测干扰内,从而多变量系统的设计问题就可以分解为各个相对独立的功能子系统的控制设计问题了,各子系统的控制算法如下:
水下航行器航向控制子系统的控制算法可以写为:
| ${{\delta }_{r}}=\left\{ \begin{array}{*{35}{l}} -{{k}_{1}}v-{{k}_{2}}r+{{(hB)}^{-1}}[{{h}_{2}}{{{\dot{r}}}_{d}}+{{h}_{3}}{{r}_{d}}-h\delta \hat{f}-\eta \text{sgn}(\sigma )] \\ \text{discontinuousversion} \\ -{{k}_{1}}v-{{k}_{2}}r+{{(hB)}^{-1}}[{{h}_{2}}{{{\dot{r}}}_{d}}+{{h}_{3}}{{r}_{d}}-h\delta \hat{f}-\eta \tanh (\frac{\sigma }{\varphi })] \\ \text{continuousversion}. \\ \end{array} \right.$ |
水下航行器横倾控制子系统的控制算法可以写为:
| ${{\delta }_{2}}=\left\{ \begin{array}{*{35}{l}} -{{k}_{1}}p-{{k}_{2}}\varphi +{{(hB)}^{-1}}[-h\delta \hat{f}-\eta \text{sgn}(\sigma )] \\ \text{discontinuousversion} \\ -{{k}_{1}}p-{{k}_{2}}\varphi +{{(hB)}^{-1}}[-h\delta \hat{f}-\eta \tanh (\frac{\sigma }{\varphi })] \\ \text{continuousversion}. \\ \end{array} \right.$ |
水下航行器潜浮控制子系统的控制算法可以写为:
| $\left[ \begin{array}{*{35}{l}} {{\delta }_{1}} \\ {{\delta }_{b}} \\ \end{array} \right]=\left\{ \begin{array}{*{35}{l}} -Kx+{{(CB)}^{-1}}[C{{{\dot{x}}}_{d}}-C\delta \hat{f}-\eta \text{sgn}(\sigma )] \\ \text{discontinuousversion} \\ -Kx+{{(CB)}^{-1}}[C{{{\dot{x}}}_{d}}-C\delta \hat{f}-\eta \tanh (\frac{\sigma }{\varphi })] \\ \text{continuousversion}. \\ \end{array} \right.$ |
应用所提出的非线性鲁棒滑模控制器,在 Matlab 与 Simulink 环境中进行仿真。
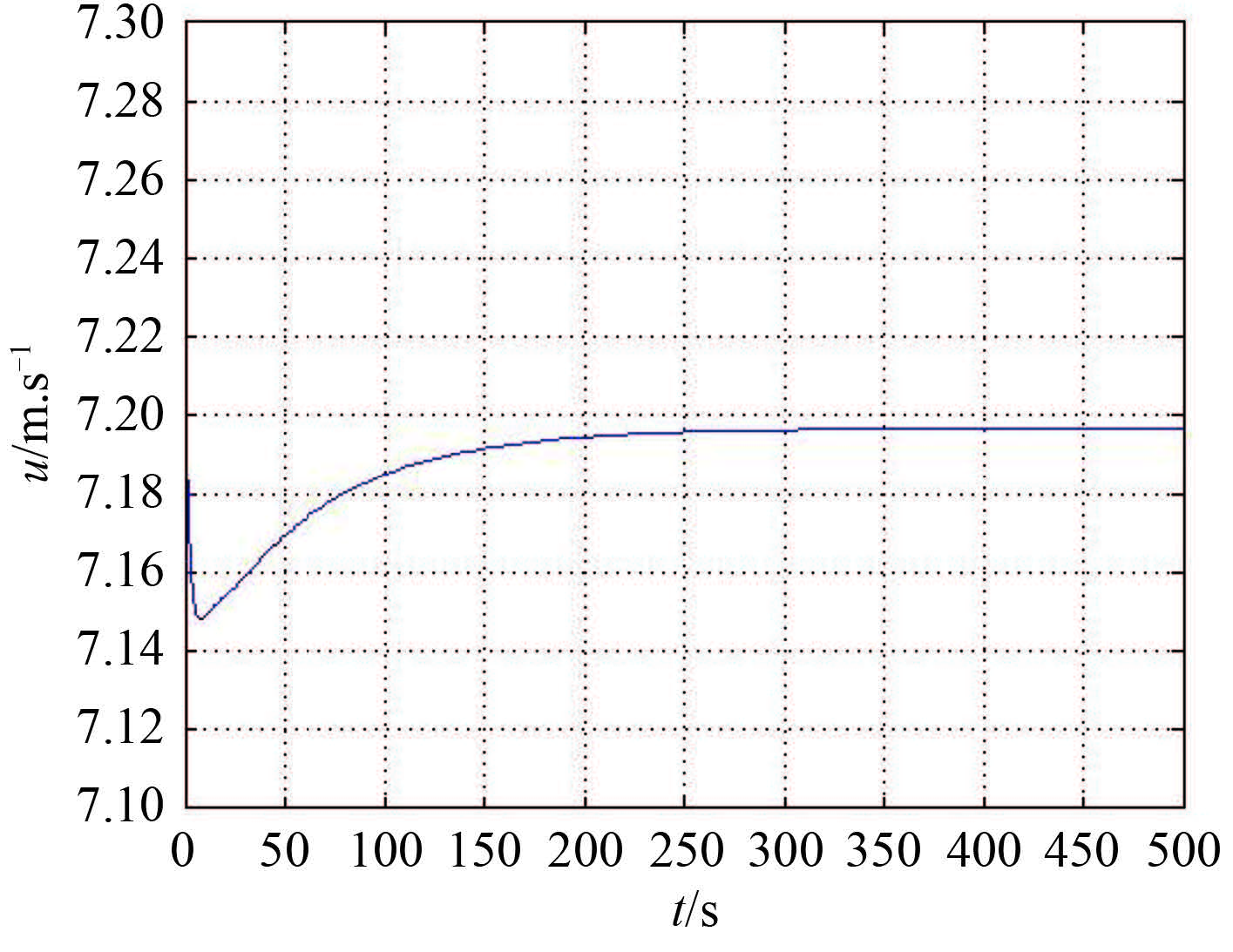
假设水下航行器的基准航速 u0 = 14 kn,水下航行器的初始深度为 100 m,水下航行器在初始时刻横倾角为 3°,转首角速度为 0.5°/s。滑模控制器的切换增益设为 η = 0.01,边界层厚度设为 φ = 0.1。应用所提出的非线性鲁棒滑模控制器,在 Matlab 与 Simulink 环境中进行仿真。图 3 ~ 图 11 给出了水下航行器定深直航过程中的状态曲线。
|
图 3 纵向速度历时曲线 Fig. 3 The curve of Longitudinal velocity |
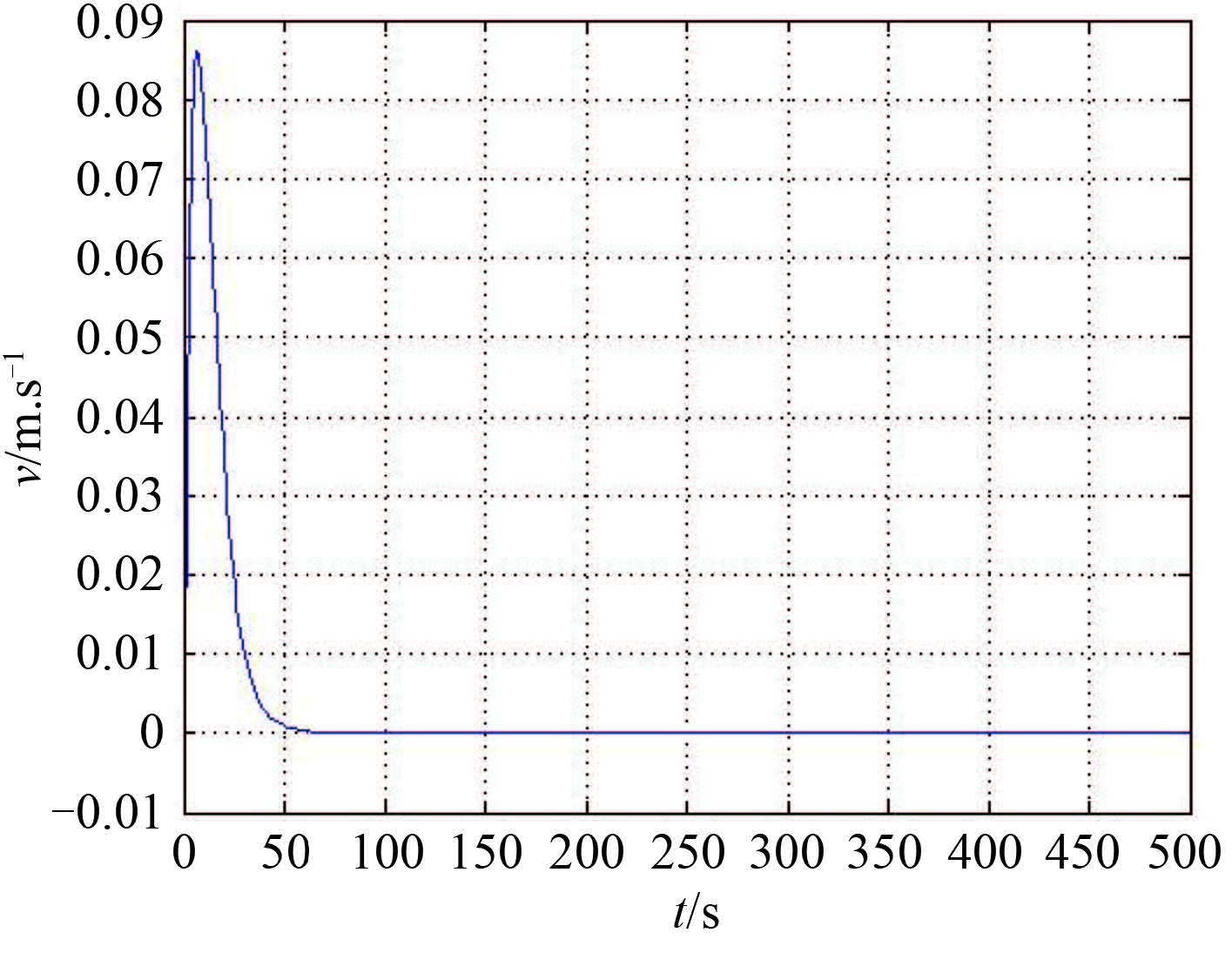
|
图 4 横向速度历时曲线 Fig. 4 The curve of transverse velocity |
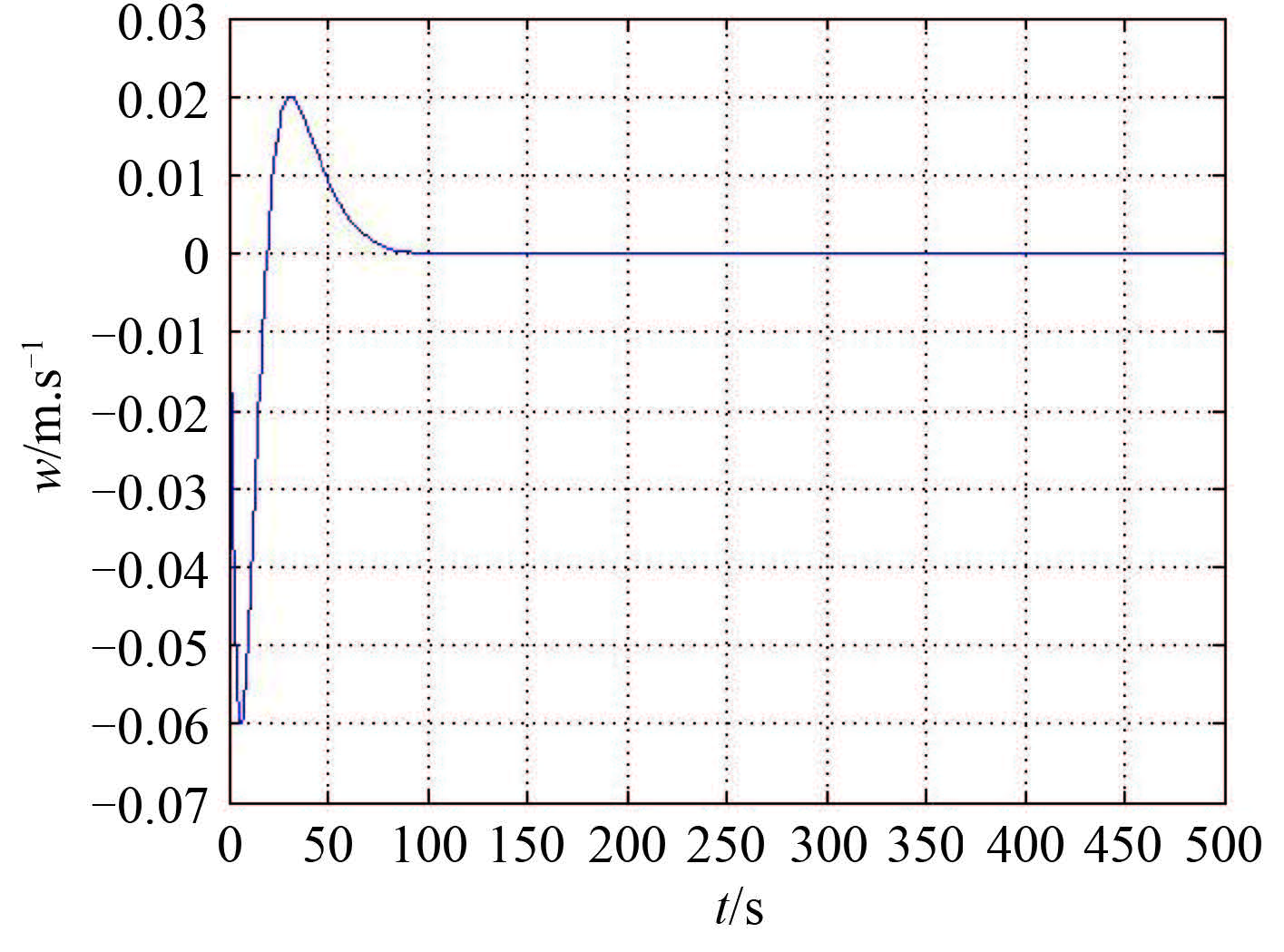
|
图 5 垂向速度历时曲线 Fig. 5 The curve of vertical velocity |

|
图 6 横倾角历时曲线 Fig. 6 The curve of heeling angle |
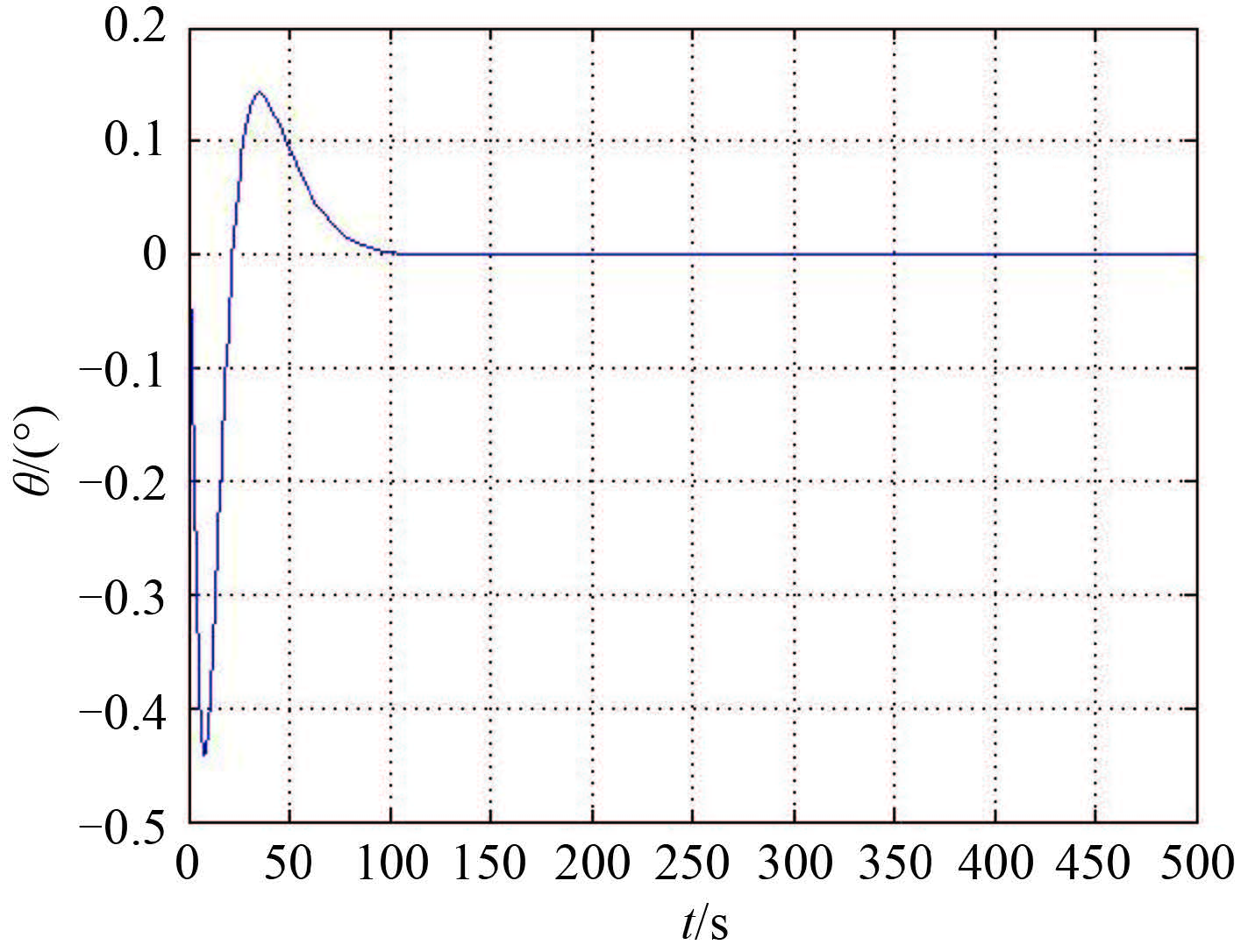
|
图 7 纵倾角历时曲线 Fig. 7 The curve of trim angle |
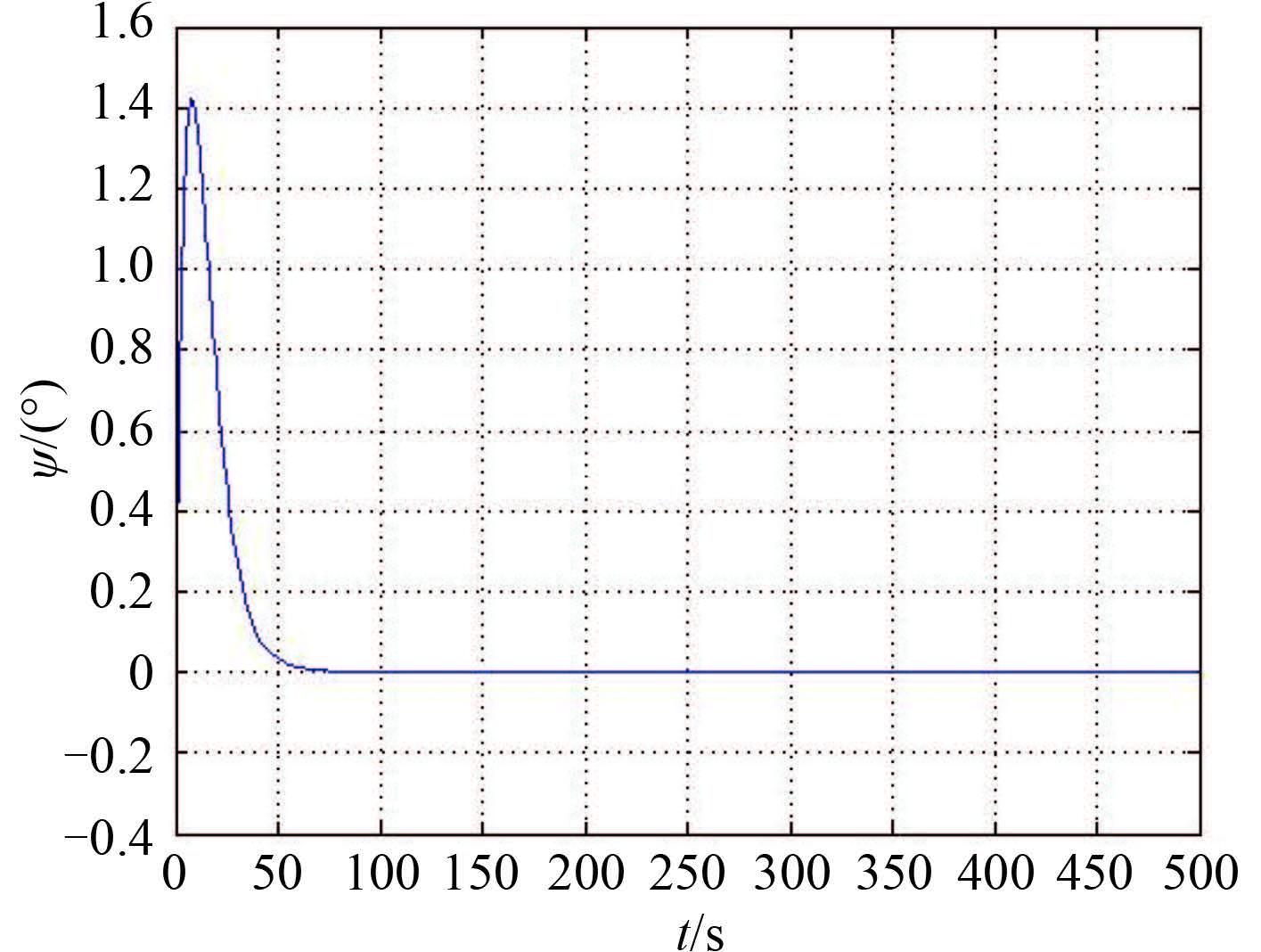
|
图 8 首向角历时曲线 Fig. 8 The curve of heading angle |
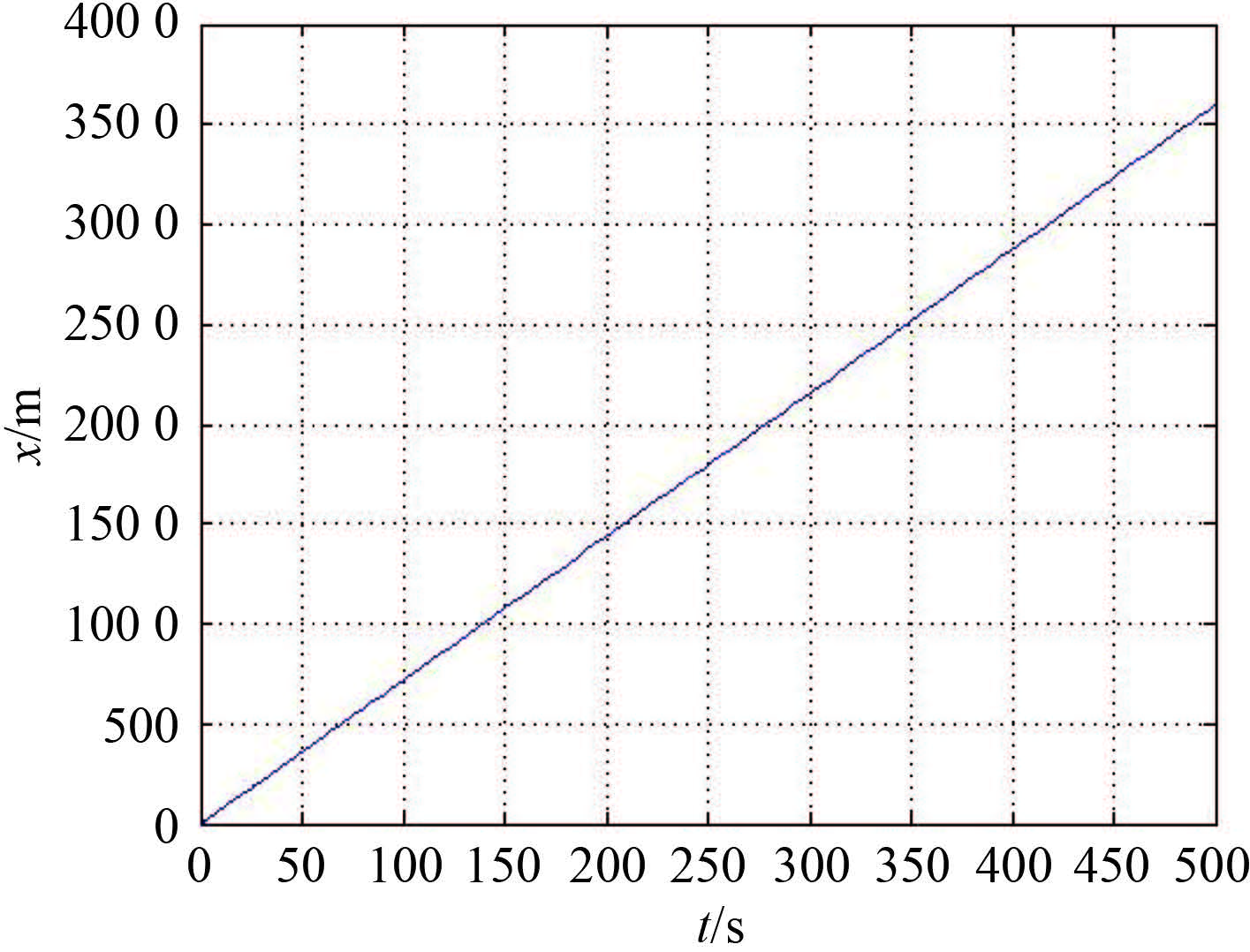
|
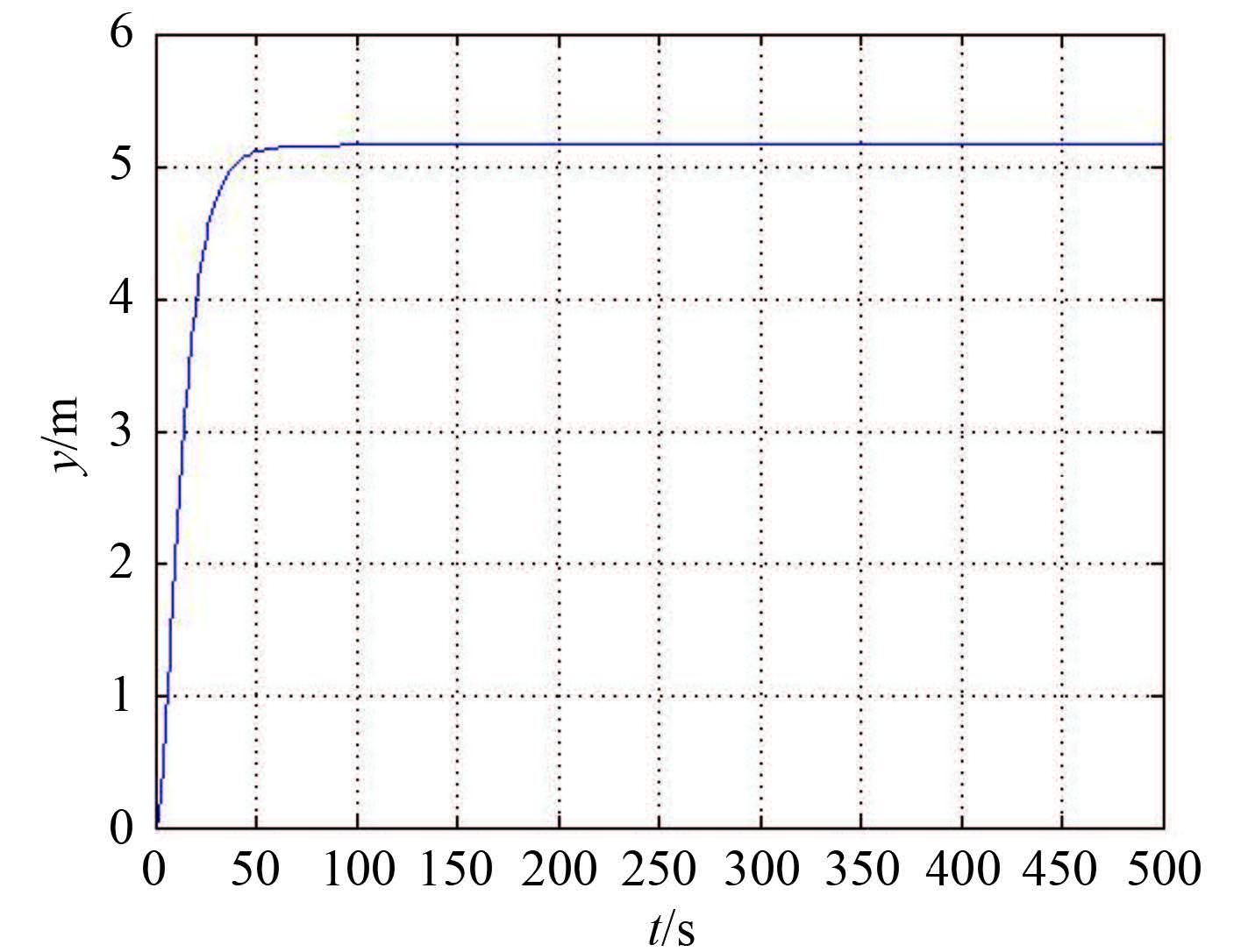
图 9 纵向位移历时曲线 Fig. 9 The curve of longitudinal displacement |
|
图 10 横向位移历时曲线 Fig. 10 The curve of lateral displacement |
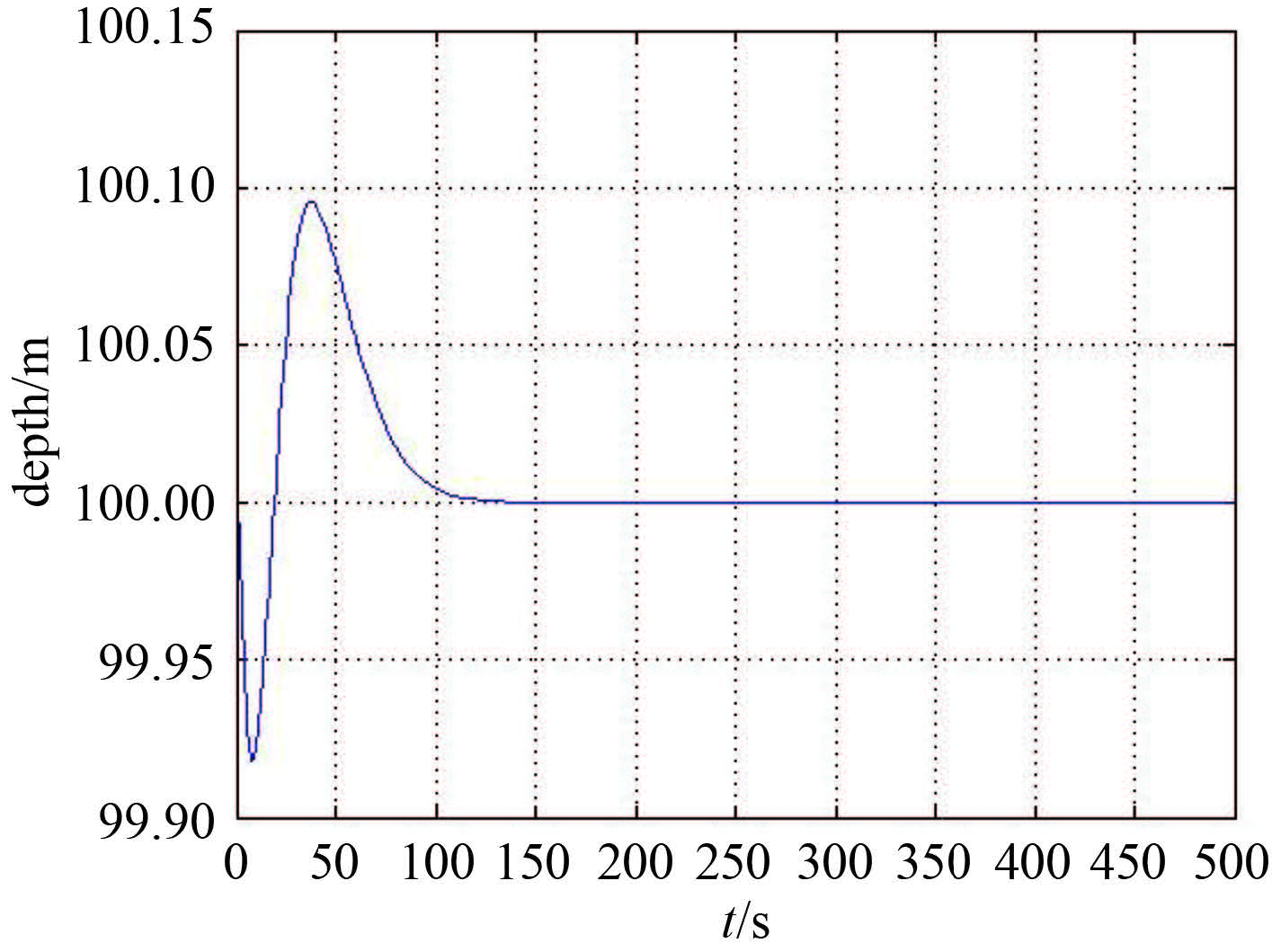
由图 11可知,在经过较短的时间后,水下航行器深度恢复到初始深度,转首角速度稳定在 0°/s,并保持定深航行。
|
图 11 深度历时曲线 Fig. 11 The curve of depth |
基于水下航行器空间运动数学模型,针对分离式尾舵且首舵收回情况下的水下航行器动态过程中存在的强耦合和非线性特点,研究了非线性鲁棒滑模控制方法的自动操纵控制方案。基于 Matlab 数值计算软件,设计完整的空间运动六自由度水下航行器动力学模型仿真模块。对水下航行器在分离式尾舵且首舵收回状态下的操纵控制方案进行仿真试验。数值仿真结果验证了该设计方法的有效性,设计出的分离式尾舵且首舵收回情况下的水下航行器操纵控制系统能够实现水下航行器的定深直航,控制效果良好。
| [1] | 施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995 : 78 -181. |
| [2] | 金鸿章, 姚绪梁. 船舶控制原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2002 : 149 -164. |
| [3] |
张瑾, 连琏, 葛彤. 潜艇近水面运动鲁棒控制及仿真研究[J]. 海洋工程 , 2006, 24 (4) :32–37.
ZHANG Jin, LIAN Lian, GE Tong. Robust control and simulation of near-surface submarine[J]. The Ocean Engineering , 2006, 24 (4) :32–37. |
| [4] |
王薇. 非线性系统的滑模控制研究[D]. 青岛:中国海洋大学, 2005:13-31.
WANG Wei. The sliding mode control of nonlinear systems[D]. Qingdao:Ocean University of China, 2005:13-31. |
| [5] | 田宏奇. 滑模控制理论及其应用[M]. 武汉: 武汉出版社, 1995 . |
| [6] | ZHAO Wen-jie, LIU Ji-zhen. An improved method of sliding mode control with boundary layer[J]. Journal of System Simulation , 2005, 17 (1) :156–158. |
| [7] |
金鸿章, 罗延明, 肖真, 等. 抑制滑模抖振的新型饱和函数法研究[J]. 哈尔滨工程大学学报 , 2007, 28 (3) :288–291.
JIN Hong-zhang, LUO Yan-ming, XIAO Zhen, et al. Investigation of a novel method of saturation function for chattering reduction of sliding mode control[J]. Journal of Harbin Engineering University , 2007, 28 (3) :288–291. |
| [8] | 李殿璞. 船舶运动与建模[M]. 哈尔滨: 哈尔滨工程大学出版社, 2005 : 214 -230. |
| [9] | 魏巍. Matlab控制工程工具箱技术手册[M]. 北京: 国防工业出版社, 2004 : 1 -4. |
| [10] | 于浩洋, 初红霞, 王希凤, 等. Matlab实用教程-控制系统仿真与应用[M]. 北京: 化学工业出版社, 2009 : 12 -14. |
 2016, Vol. 38
2016, Vol. 38
