2. 水下信息与控制重点实验室, 陕西 西安 710077
2. Science and Technology on Underwater Information and Control Laboratory, Xi'an 710077, China
在采用冷凝器的水下航行器动力系统中,由于没有尾气排放,系统与外界只有热量交换而无物质交换,做功后的乏汽必须经冷凝器冷凝成水后才能供给系统作为循环工质使用,而布置在冷凝器上的小通道是动力系统与外界交换热量的最主要部件。小通道换热能力的高低直接影响着冷凝器乃至于整个水下航行器的航行性能。因此在采用冷凝器的水下航行器的工程设计上,关于小通道内蒸汽冷凝换热特性的计算分析是必不可少的一环[1-2]。
小通道的概念主要应用在具有高换热效率的紧凑型换热器上,小通道内的冷凝换热过程主要在传统工业电子设备的热管,紧凑式换热器以及冷藏冷冻等领域研究[3-4]。
通过查阅国内外文献资料发现,众多学者针对传统工业上使用的小通道内的冷凝换热特性进行了大量的研究[5-8]。但是针对水下航行器这一特殊的结构限制,其小通道当量直径为 4.4~8.9 mm,而且通道内需要冷凝换热的是具有高热通量高流速的过热水蒸汽,在这一特殊使用环境内的小通道蒸汽冷凝换热特性方面的研究则较少。
因此针对水下航行器用小通道蒸汽的冷凝换热研究具有工程价值和理论意义。本文将建立矩形小通道冷凝换热过程的数理模型,对其进行仿真计算,以获得矩形小通道内的流动换热特性,为水下航行器的工程应用提供理论支持与数据支撑。
1 蒸汽凝结换热模型本文针对矩形直通道中蒸汽凝结换热特性进行理论建模研究。在建立模型方程时,根据工质的状态变化把整个过程分为过热蒸汽段、气液两相段(饱和段)及过冷水段 3 段。通过干度判断沿程工质状态,结合其物性变化,对每个阶段的传热传质分别求解。
1.1 凝结换热模型小通道是冷凝器中的重要结构部件,在建模的过程中要考虑冷凝器的结构特性,由于水下航行器用冷凝器特殊的使用环境,在冷凝器圆周布置有矩形冷却通道。小流径通道除了外管壁为与冷却水直接接触的换热壁面外,两边的端壁也是换热壁面。
建立计算模型时首先假设:
1)冷却通道间壁认为是强化传热肋片,在计算时考虑翅片效率;
2)通道外部的冷却水温度为常温;
3)小通道内流动为稳态流动;
4)内管壁视为绝热,不计导热及散热损失的影响。
5)不考虑重力的影响。
根据上述假设,考察如图 1 所示的控制体,微元段长度为 dx,微元段进口质量流量为 ${{{\dot m}}_{{in}}}$,微元段出口质量流量为 ${{{\dot m}}_{{out}}}$,微元段进口蒸汽温度为 ${T_{cd}}$,外管壁温度为 ${T_w}$,外部冷却水温度为 ${T_{sw}}$,内管壁视为绝热。
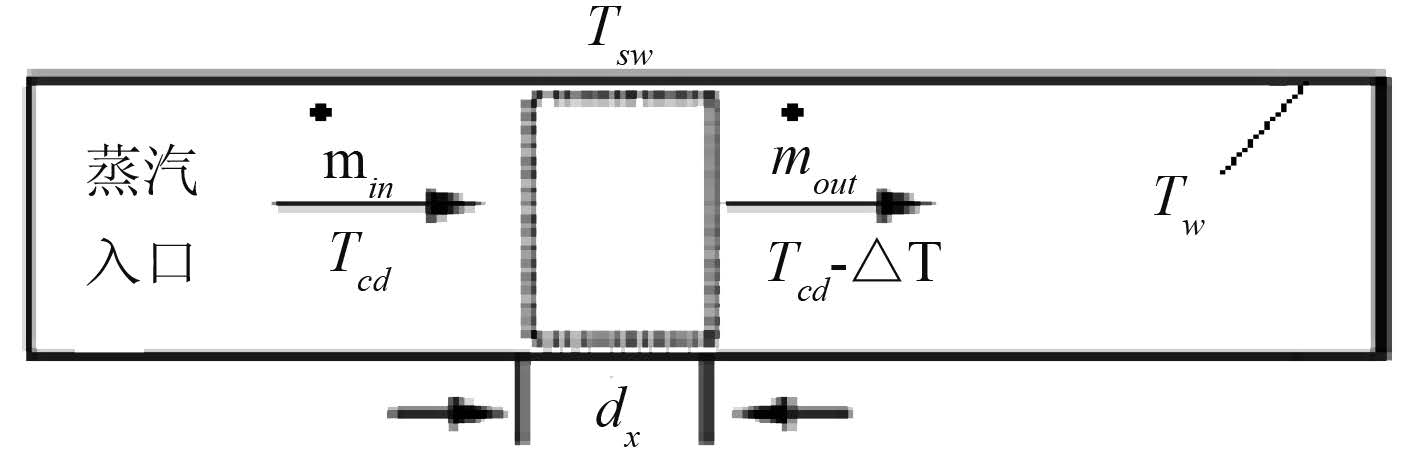
|
图 1 换热过程简化模型示意图 Fig. 1 The simplified model for heat transfer process |
根据热力学第一定律可知:热力系总能量的增量等于加入热力系的能量总和与热力系输出的能量总和之差[9],即
| $\delta Q=dE+({{e}_{2}}\delta {{m}_{2}}-{{e}_{1}}\delta {{m}_{1}})+\delta {{W}_{\text{out}}}$ | (1) |
式中:Q 为热力系从外界吸收的热量;E 为热力系具有的能量;e1,e2 为流入、流出热力系的微元每千克能量;$\delta {m_1}$,$\delta {{{m}}_2}$ 为流入流出热力系的微元质量;$\delta {W_{{out}}}$ 为微元段对外界做出的功;
将热力学第一定律用于矩形小通道内的蒸汽流动换热过程可得,蒸汽与冷凝壁面的对流换热一般过程换热模型如下:
| ${{\dot{m}}_{in}}\text{d}H-{{h}_{cd}}({{T}_{w}}-{{T}_{cd}})\text{zd}l=0\text{,}$ | (2) |
式中:${\dot m_{in}}$ 为通道入口蒸汽质量流量;H 为蒸汽焓值;${h_{cd}}$ 为蒸汽与壁面对流换热系数;${T_{cd}}$ 为蒸汽温度;z 为冷却通道宽度;${\text{d}}l$ 为计算微元段通道长度,对矩形直通道而言,dl = dx;
不同通道间壁面也参与换热,因此本论文所研究的小流径通道间壁要按强化传热肋片考虑,在蒸汽与冷凝壁面的对流换热方程(2)中要加入传热肋片效率这一影响因素,因此适用于本论文的过热蒸汽与冷凝壁面的对流换热过程方程式如下:
| ${{\dot{m}}_{in}}\text{d}H-{{h}_{cd}}({{T}_{w}}-{{T}_{cd}})(y+2z{{\eta }_{f}})\text{d}l=0,$ | (3) |
式中:y 为冷却通道高度;${\eta _{_f}}$ 为冷却通道两侧强化传热肋片效率。
其中,在冷却通道的计算过程中采用冷却通道两侧强化传热肋片效率 ${\eta _f}$ 计算公式为:
| ${{\eta }_{f}}=\frac{\text{th}({{m}_{cd}}h)}{{{m}_{cd}}h}\text{,}$ | (4) |
| ${{m}_{cd}}=\sqrt{\frac{2{{\varsigma }_{cd}}}{{{\lambda }_{cd}}{{\sigma }_{cd}}}},$ | (5) |
式中:th 为双曲正切函数;${m_{cd}}$ 为翅片参数;${\lambda _{cd}}$ 为材料的导热系数;${\sigma _{cd}}$ 为冷却通道间壁厚度;${h_{cd}}$ 为蒸汽与壁面的流换热系数;h 为肋片高度。
而冷凝壁面与外部冷却水的对流换热过程:
| ${{\dot{m}}_{in}}\text{d}H-{{h}_{0}}(z+{{\sigma }_{cd}})({{T}_{sw}}-{{T}_{w}})\text{d}x=0\text{,}$ | (6) |
其中 ${h_0}$ 为外部冷却水与冷凝壁面的对流换热系数。
经整理可得冷却通道内蒸汽焓值函数的微分方程为:
| $\frac{\text{d}H}{\text{d}x}=\frac{{{h}_{cd}}({{T}_{sw}}-{{T}_{cd}})(z+2y{{\eta }_{f}})}{{{{\dot{m}}}_{in}}+\frac{{{h}_{cd}}{{{\dot{m}}}_{in}}}{{{h}_{0}}(z+{{\sigma }_{cd}})}(z+2y{{\eta }_{f}})}\circ $ | (7) |
蒸汽在矩形小通道管内凝结换热过程,按照蒸汽的状态把整个过程分为过热蒸汽段、气液两相段及过冷水段 3 段。假设冷却水侧的温度不变。
1)在过热区和过冷区
过热蒸汽的对流换热系数:
| ${{h}_{cd}}=\frac{Nu\cdot {{\lambda }_{cd}}}{{{d}_{ecd}}},$ | (8) |
式中:${h_{cd}}$ 为蒸汽的导热系数;${d_{ecd}}$ 为流体管路的当量直径;$Nu$ 为努赛尔数,表征壁面上流体的无量纲温度;
$Nu$ 数可用采用对流传热理论中的特征数方式(实验关联式)来表示:
| $Nu=C\text{Re}_{m}^{a}\underset{m}{\overset{b}{\mathop{Pr}}}\,$ | (9) |
2)在两相区
由于两相区为气相液相互相掺混流动,其传热特性及其复杂,目前主要通过从层流液膜厚度出发的 Nusselt 理论计算关系式和以大量实验数据为基础进而总结出的实验关联计算式来分别进行研究。
①Nusselt 计算关系式
Nusselt 提出了纯净蒸汽层流膜状凝结的分析解,对于水平管上的层流膜状凝结,其平均表面传热系数的计算式为[10]:
| ${{h}_{H}}=0.875{{\left[ \frac{gr\rho _{\text{l}}^{\text{2}}\lambda _{\text{l}}^{\text{3}}}{{{\eta }_{\text{l}}}d({{T}_{\text{s}}}-{{T}_{\text{w}}})} \right]}^{0.25}}\circ $ | (10) |
式中:g 为重力加速度;r 为汽化潜热;ρl 为液相密度;λl 为液相导热系数;d 为水平管直径;ηl 为液相动力粘度;Tw 为壁面温度;Ts 为蒸汽饱和温度。
②Akers-Rosson 实验关联计算式
在研究气液两相区域蒸汽凝结传热的过程中,前人总结大量实验数据得到的一些关联式具有一定的认可度,可使用 Akers 和 Rosson 的关联式[11],得到两相区平均对流传热系数为:
| ${{h}_{cd}}=0.026\ 5\frac{{{\lambda }_{cd}}}{d{{e}_{cd}}}R{{e}_{eq}}^{0.8}P{{r}_{m}}^{1/3}\circ $ | (11) |
式中 $R{e_{eq}}$ 为当量雷诺数,使用该式时要求 Reeq>50 000。
而通道内平均对流换热系数:
| $h=\frac{\sum\limits_{{}}^{{}}{{{h}_{i}}}}{N}\circ $ | (12) |
式中:${h_i}$ 为通道内各微段对流换热系数;N 为微元段数。
1.4 压力求解模型计算微元段的压力降主要由摩擦阻力压力降、加速压力降和局部阻力组成。在冷凝过程中,加速压力降和局部阻力相对摩擦压降很小可忽略不计,因此只考虑摩擦压降。
1)过热段和过冷段摩擦阻力压力降
过热段和过冷段,为单相对流换热过程,其摩擦阻力压降的计算目前已经相对准确,可采用达西(Darcy)公式来计算:
摩擦阻力压力降 $\Delta {P_{cd}}$ 可表示为:
| $\Delta {{p}_{cd}}=\lambda \frac{l}{d}\frac{\rho {{V}^{2}}}{2},$ | (13) |
则通道内过热段和过冷段摩擦阻力压力降 $\Delta {P_{cd}}$ 的计算公式为:
| $\Delta {{P}_{cd}}={{f}_{cd}}\frac{{{L}_{cd}}^{\prime }}{d{{e}_{cd}}}\frac{{{\rho }_{\text{m}}}{{u}_{cd,m}}^{2}}{2}\circ $ | (14) |
式中:${f_{cd}}$ 为流体摩擦阻力系数;${L_{cd}}^\prime $ 为冷却通道长度;${u_{cd,m}}$ 为流体的流速。
其中摩擦阻力系数 ${f_{cd}}$ 计算公式采用 Blasius 关联式:
| ${{f}_{cd}}=\left\{ \begin{array}{*{35}{l}} 16/R{{e}_{cd,m}}, & 0<R{{e}_{cd,m}}<2\ 500; \\ 0.079R{{e}_{cd,m}}^{-0.25}, & 2\ 500<R{{e}_{cd,m}}<20\ 000; \\ 0.046R{{e}_{cd,m}}^{-0.2}, & R{{e}_{cd,m}}>20\ 000 \\ \end{array} \right.$ | (15) |
2)对于饱和段即凝结段摩擦阻力压降
两相流体的摩擦阻力压力目前尚无精确的计算公式,可参考文献中的摩擦阻力压降公式来求取[4]:
| $\Delta {{P}_{sa}}=4{{f}_{cd}}^{\prime }\frac{{{L}_{cd}}^{\prime }}{d{{e}_{cd}}^{3}}\frac{R{{e}_{eq}}^{2}{{\mu }_{l}}^{2}}{2{{\rho }_{l}}}\circ $ | (16) |
式中:${\mu _l}$ 为饱和水动力粘度系数;${\rho _l}$ 为饱和水密度。
其中摩擦阻力系数 ${f_{cd}}^\prime $ 采用 C-Y.Yang 和 R.L.Webb 推荐的摩擦因子关联式[12]:
| ${{f}_{cd}}^{\prime }=0.043\ 5R{{e}_{eq}}^{0.12}{{f}_{cd}}\circ $ | (17) |
根据前节所述的冷凝器内小通道冷凝换热模型,编制仿真过程的计算流程。由于过热蒸汽在流动过程中逐渐由气相转变为液相,而在单相区和两相区需要分别采用不同的经验关联式进行计算,故在计算流程中需要判断进入两相区和进入液相区的时刻,然后根据不同区域的求解模型进行求解。
2.2 仿真模型对比根据小通道内蒸汽冷凝换热一维仿真计算模型,使用 Matlab 软件的 Simulink 工具箱编制仿真计算程序。
1)不同区域模型参数的选取
在第 1 节的对流换热模型中,过热段和过冷段模型中计算对流换热系数的换热关联式(9)中的参数 C,n,m 根据实验经验可选择不同的数值。
① 目前应用比较普遍的是 Dittus 和 Boelter 总结的实验关联式:
| $Nu=0.023R{{e}^{0.8}}Pr0.3,$ | (18) |
参数 C 取 0.023,n 取 0.8,m 取 0.3(加热流体时 m 取 0.4,其余参数取值不变)。式(19)适用范围为 104<Re<1.2 <105,管长与管径比值 ≥ 60。
② Debray.F 等[12]于 2001 年提出了单相换热实验关联式:
| $Nu=0.059\ 3R{{e}^{3/4}}P{{r}^{1/3}}\circ $ | (19) |
参数 C 取 0.059 3,n 取 3/4,m 取 1/3。其适用范围为 3 000<Re <105。
两相区的换热计算经验关联式主要有:
Nusselt 计算关系式
| ${{h}_{cd}}=0.875{{\left[ \frac{gr\rho _{cd}^{\text{2}}\lambda _{cd}^{\text{3}}}{{{\eta }_{cd}}{{d}_{ecd}}({{t}_{\text{s}}}-{{t}_{\text{w}}})} \right]}^{0.25}};$ | (20) |
Akers-Rosson 实验关联式
| ${{h}_{cd}}=0.026\ 5\frac{{{\lambda }_{cd}}}{d{{e}_{cd}}}R{{e}_{eq}}^{0.8}P{{r}_{m}}^{1/3}\circ $ | (21) |
仿真时可选取不同的计算关联式进行仿真计算并对比分析。
2)不同模型的计算式仿真对比
为针对同一工况参数下,选取不同的计算模型参数进行仿真计算,其中:模型 1 过热区和过冷区采用式(18),两相区采用式(20);模型 2 过热区和过冷区采用式(19),两相区采用式(20);模型 3 过热区和过冷区采用式(18),两相区采用式(21);模型 4 过热区和过冷区采用式(19),两相区采用式(21)。
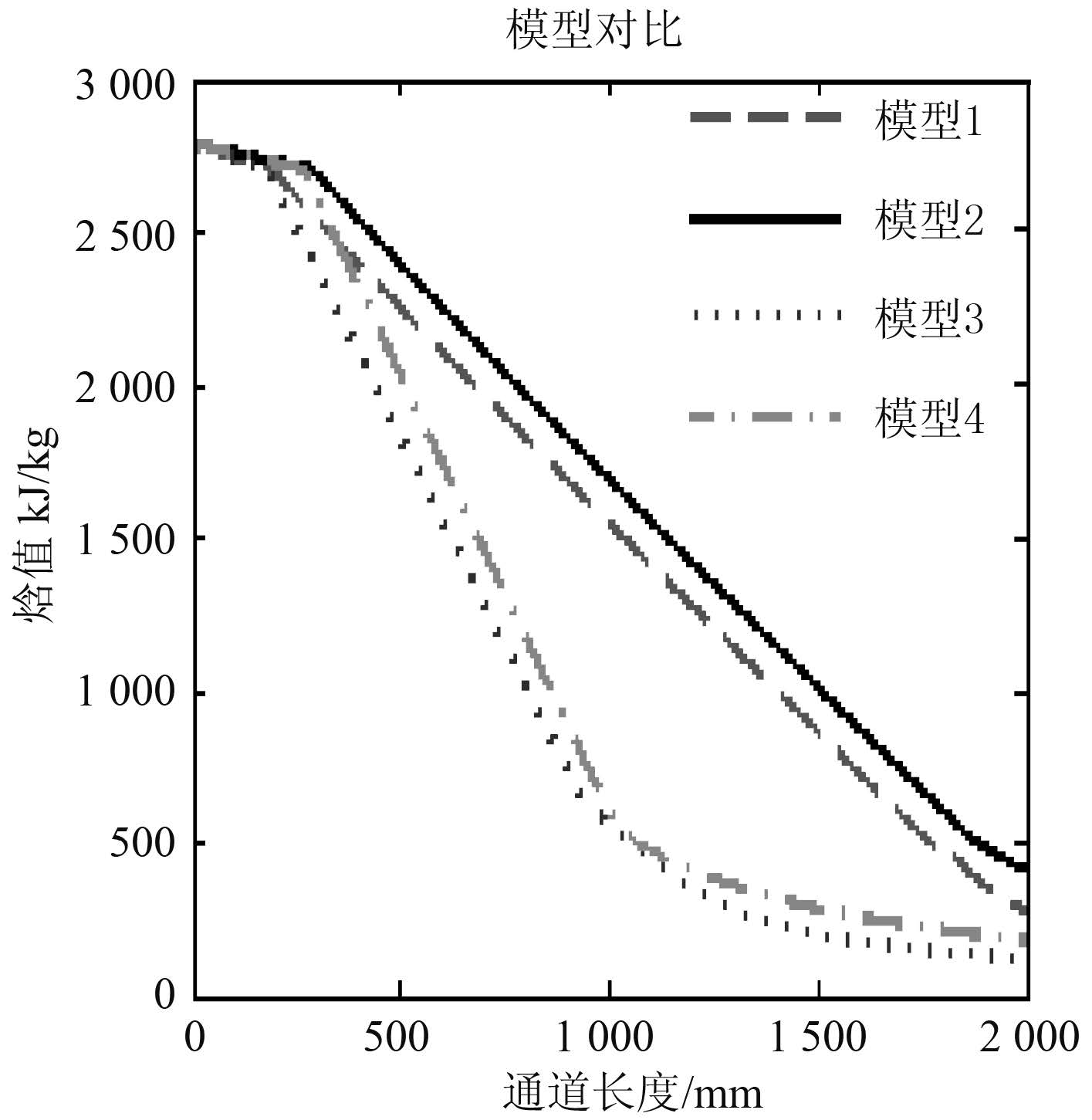
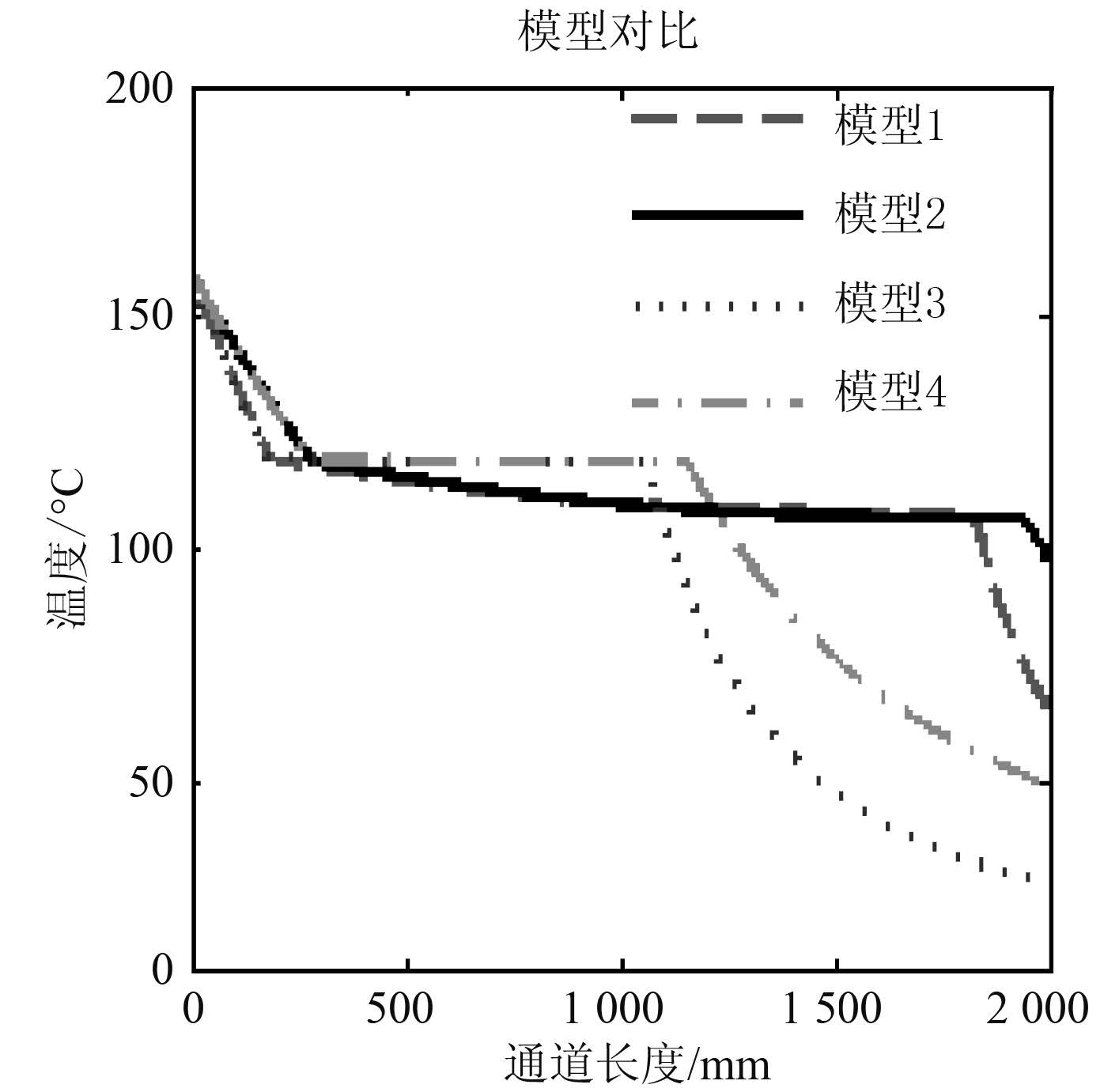
图 2从不同模型计算式的仿真结果图中可看到,在过热区和过冷区即单相对流换热区,不同模型的变化趋势基本一致。在两相换热区,模型间差别比较大,尤其是在相同蒸汽入口条件下,蒸汽完全冷凝点所在位置(即在温度对比图 3 中曲线第 2 个拐点位置),Nusselt 计算式和 Akers-Rosson 实验关联式差别比较大,从图中可知,在两相区采用式(21)Akers-Rosson 实验关联式得到的蒸汽完全冷凝点位置在距进口 1 050 mm 处附近,而采用 Nusselt 计算式(20)仿真得到的蒸汽完全冷凝点则延后至距进口 1 800 mm 处附近。
|
图 2 沿程焓值对比 Fig. 2 Enthalpy value contrast |
|
图 3 沿程温度对比 Fig. 3 Temperature contrast |
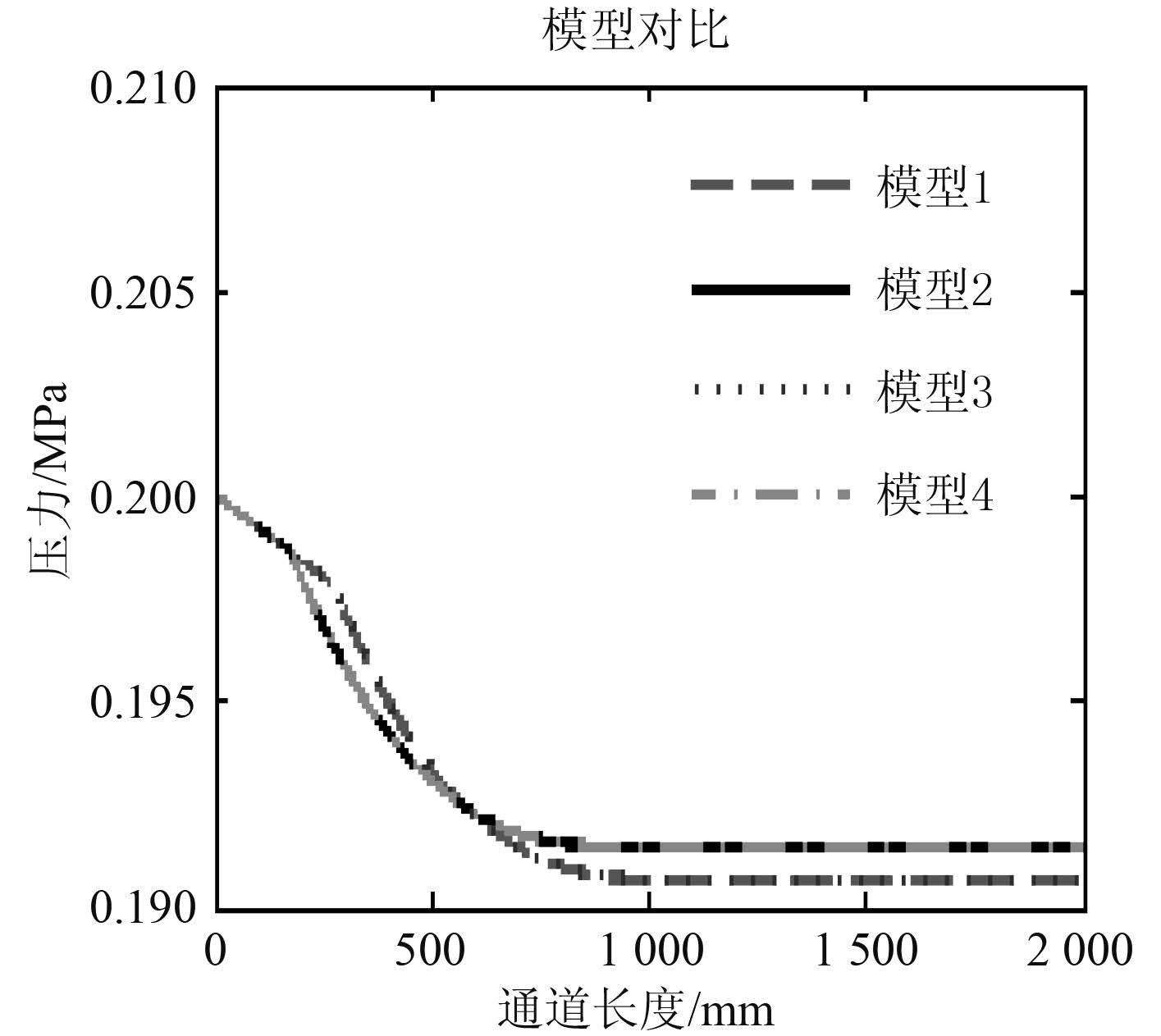
图 4针对小通道内的蒸汽凝结换热特性进行实验研究,通过实验验证所建立的凝结换热模型。根据冷凝器的使用环境和结构特点,设计了小通道冷凝换热实验系统,搭建了小通道冷凝换热实验台,并且对小通道内的蒸汽温度参数进行了实验数据的采集。
|
图 4 沿程压力对比 Fig. 4 Pressure contrast |
通过测量蒸汽和冷却水的流量、进出口的温度、进出口的压力、小通道空间中心处的温度值以及蒸汽空间中心处的压力值,可以获得蒸汽空间内沿流动方向的温度分布、压力分布,以及冷却水空间内沿流动方向的温度分布
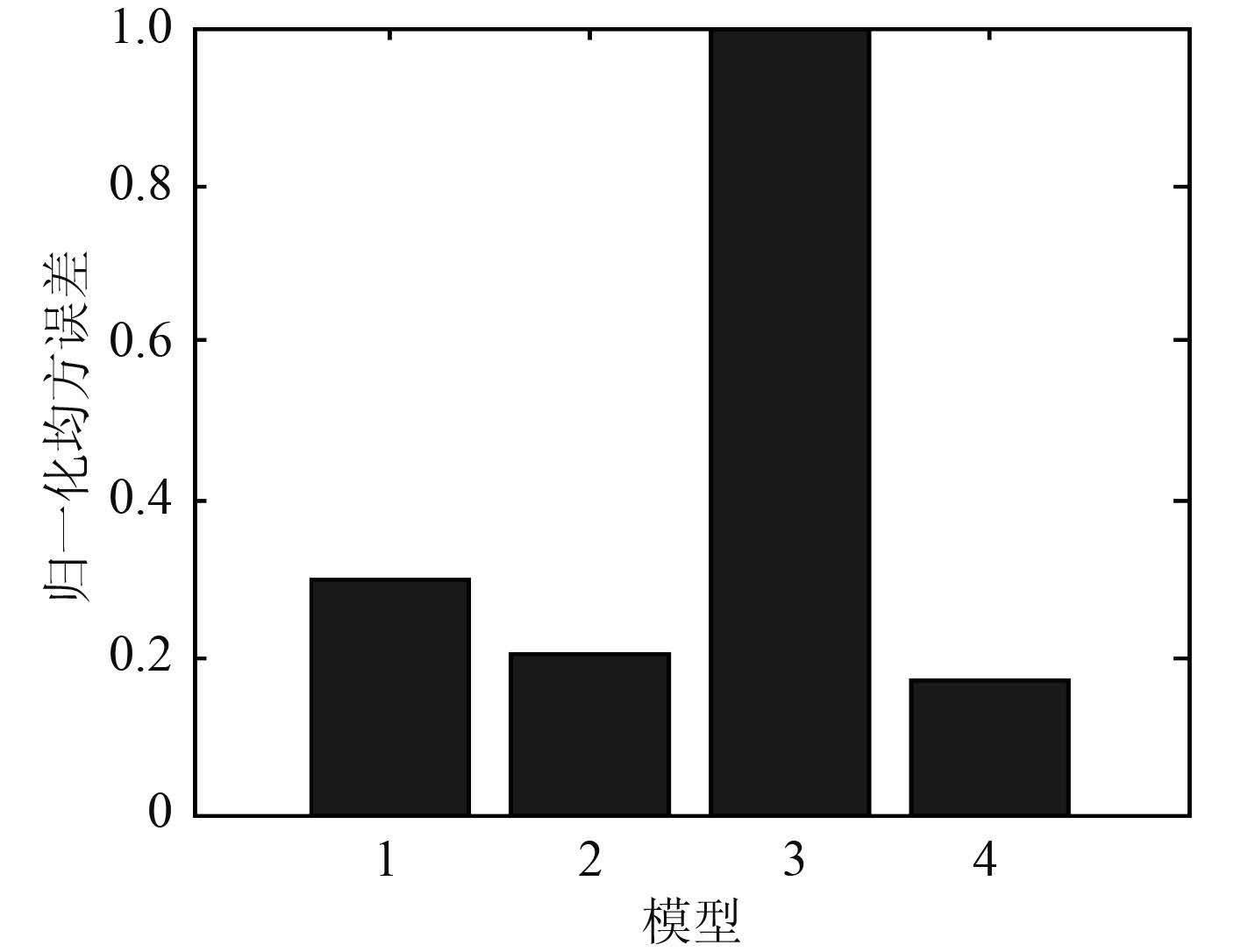
根据实验测得的温度数据对 4 组模型进行仿真计算对比,得到的结论如下:
从不同模型与实验值的对比图可知,从趋势上看,模型 3 和 模型 4 与实验结果最为接近。尤其在蒸汽通道后段,两相区向过冷区的转变点,相比于模型 1 和 模型 2,模型 3 和 模型 4 与实验值更为吻合。
从模型仿真值与对应实验点处值的误差百分比可知,与实验值进行对比,模型 4 的误差在 3%~– 30% 之间,而模型 3 的误差值在 2%~– 60%,虽然模型 2 的误差值在 20%~– 10%,在这 4 组模型中误差振幅最小,但是从归一化的均方误差来看,模型 4 的归一化均方误差值最小,在 4 组模型中与实验值拟合最好。
图 5-图 9因此,可采用模型 4 对水下航行器用小通道内蒸汽冷凝换热特性进行设计计算。
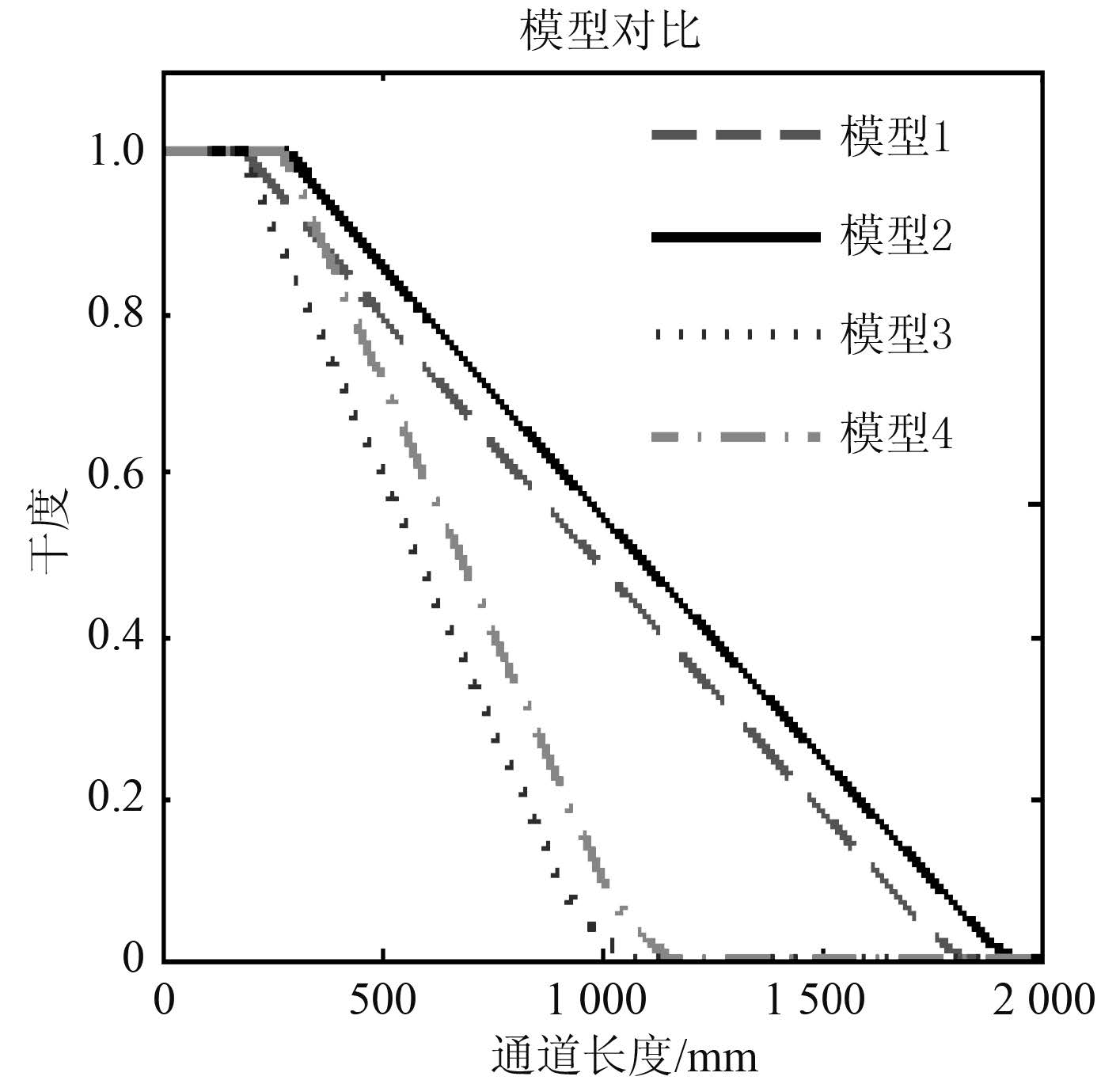
|
图 5 沿程干度对比 Fig. 5 Dry degree contrast |
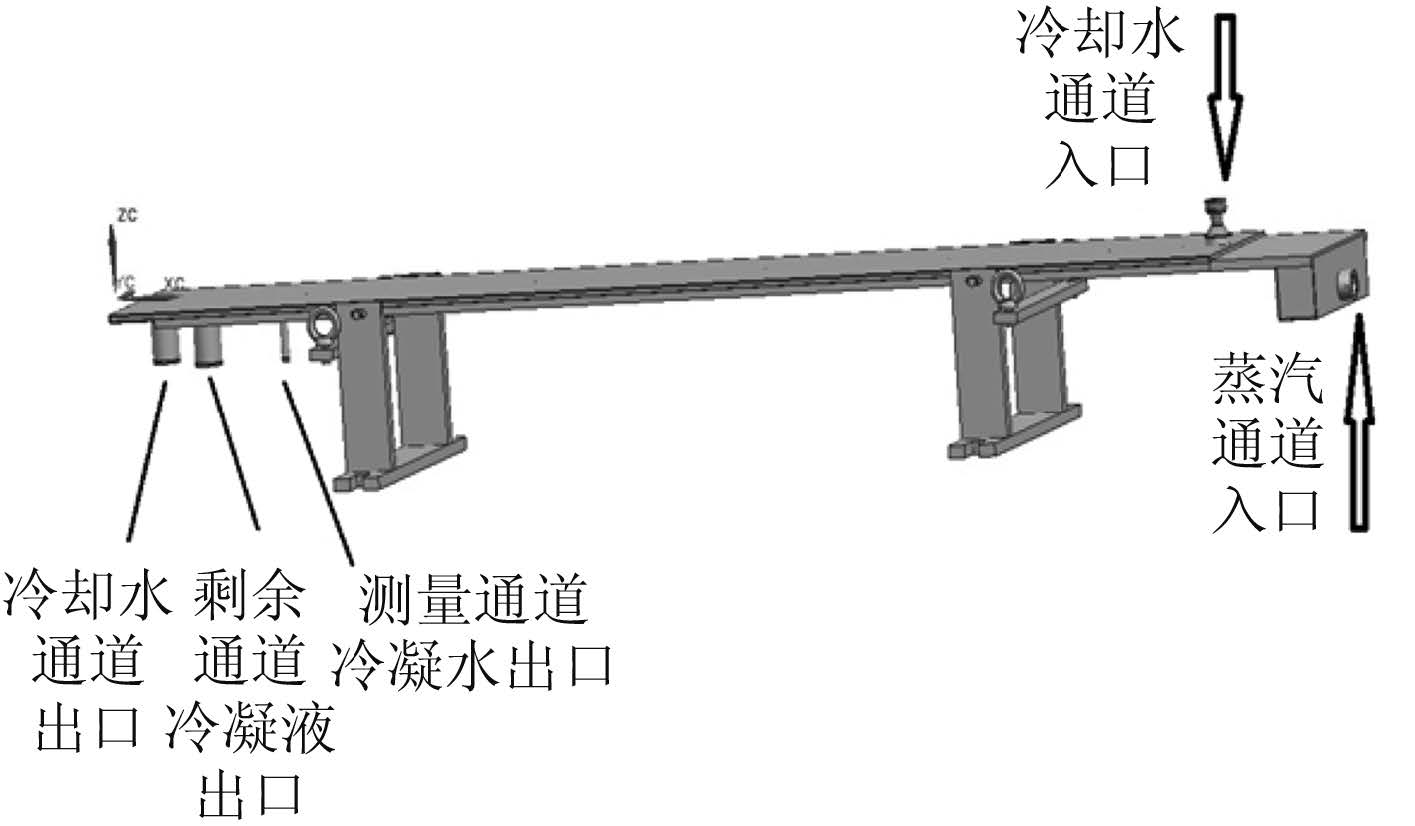
|
图 6 小通道冷凝换热装置三维图 Fig. 6 Small channel condensation heat exchange device |
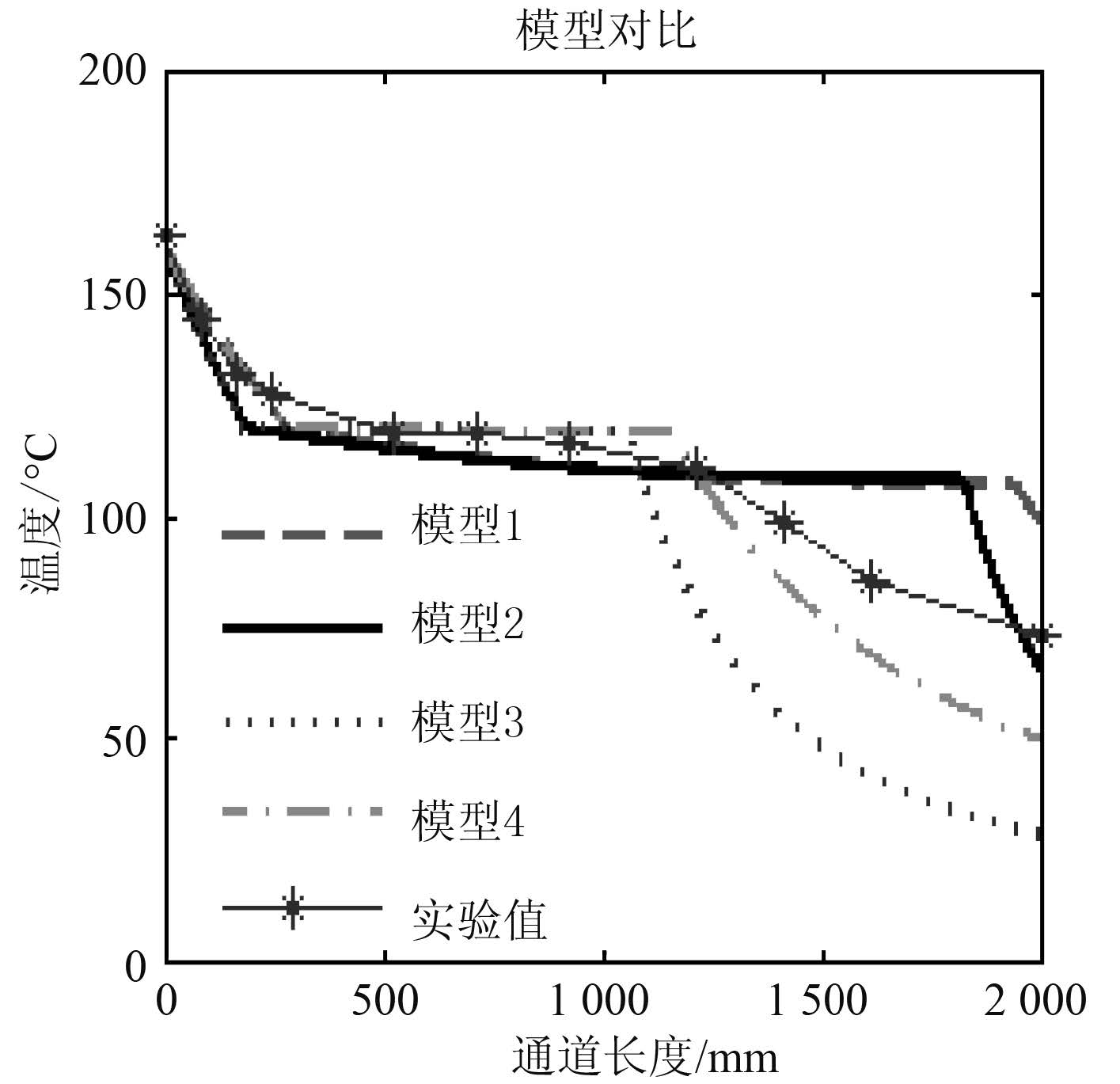
|
图 7 不同模型与实验值对比图 Fig. 7 Comparison of model and experimental results |
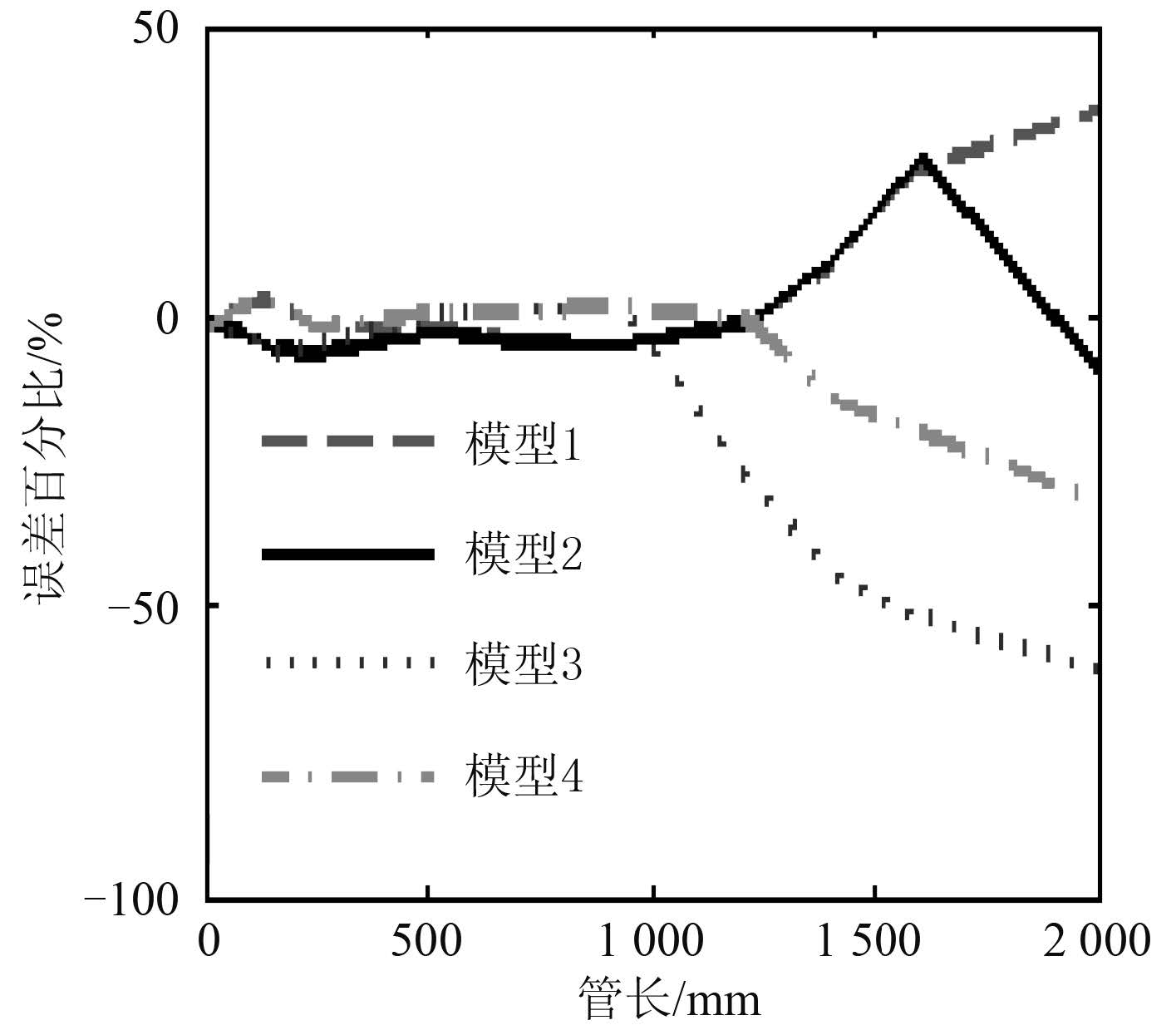
|
图 8 不同模型误差趋势图 Fig. 8 Error trend of models |
|
图 9 不同模型归一化均方误差 Fig. 9 Normalized mean square error |
根据水下航行器的结构特性,其内部用于换热的冷凝器中冷却通道为螺旋状矩形管,在航行器内外壳体之间狭小空间布置冷凝器的换热通道,根据水下航行器壳体强度计算并综合其他部件的结构尺寸,小通道在高度方向上的尺寸基本确定为 5 mm。在宽度方向上,结合水下航行器壳体直径限制以及结构强度设计要求,在宽度方向的选取值一般在 4~8 mm 之间。
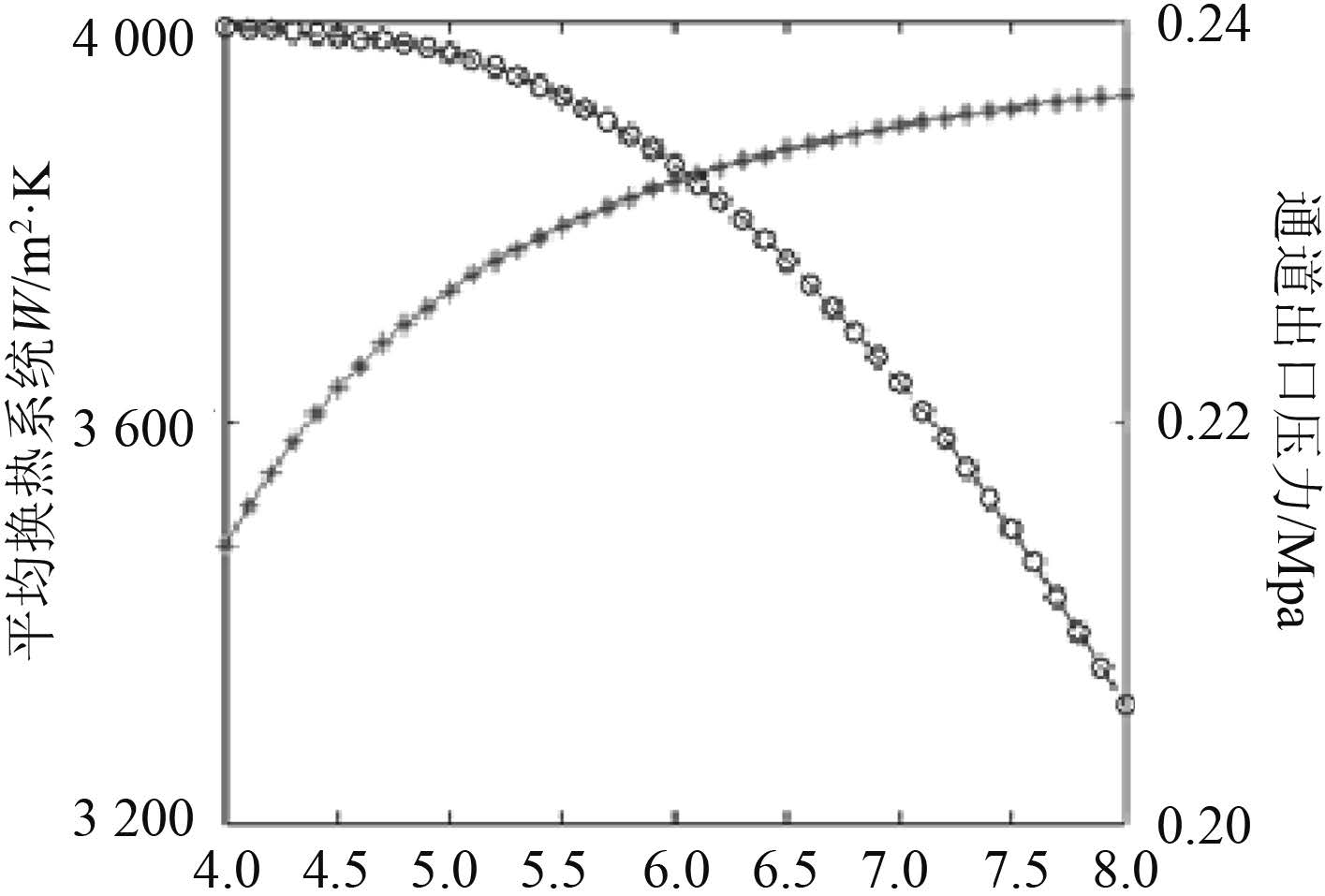
采用模型 4 对水下航行器中的小通道不同截面尺寸进行流动换热能力的计算分析,得到结果如图 10 所示。
|
图 10 通道截面宽度参数对换热系数和出口压力的影响 Fig. 10 The effect of width on the heat transfer coefficient and outlet pressure |
从图 10 可看出,随着通道截面宽度的增加,通道内平均换热系数的下降和通道出口压力的增大有一个相对平衡点,即在通道截面宽度为 6 mm 左右(6.03 mm)的时候,通道内的蒸汽凝结换热过程具有较大的平均换热系数和较小的压力损失。
综合考虑,在水下航行器的工程设计上,选取 5 mm × 6 mm 尺寸的通道具有较好的流动换热效果。
3 结 语根据建立的水下航行器用冷凝器中小流径通道的凝结换热模型,进行仿真计算,结合实验数据对比,得到适用于水下航行器的小通道内蒸汽凝结换热模型参数。即在单相区采用 D-B 实验关联计算式,在两相区采用 A-R 实验关联计算式。并根据得到的模型参数,进行水下航行器的小通道截面尺寸计算设计,得到在水下航行器用小通道中采用 5 mm × 6 mm 截面尺寸具有较好的流动换热效果。
采用模型 4 中的计算式以及 5 mm × 6 mm 截面尺寸对水下航行器用小通道的工程设计具有重要的参考价值。
| [1] |
查志武, 史小锋, 钱志博.
鱼雷热动力技术[M]. 北京: 国防工业出版社, 2006 .
ZHA Zhi-wu, SHI Xiao-feng, QIAN Zhi-bo. Technique of torpedo thermal power[M]. Beijing: National Defence Industry Press, 2006 . |
| [2] |
郝保安, 孙起.
水下制导武器[M]. 北京: 国防工业出版社, 2014 .
HAO Bao-an, SUN Qi. Underwater guided weapons[M]. Beijing: National Defence Industry Press, 2014 . |
| [3] |
章熙民, 任泽霈, 梅飞鸣.
传热学[M]. 北京: 中国建筑工业出版社, 2007 .
ZHANG Xi-min, REN Ze-pei, MEI Fei-ming. Heat transfer[M]. Beijing: China Architecture & Building Press, 2007 . |
| [4] |
朱晓红, 李海东, 张卫东. 船用膜式螺旋管换热器传热和流动特性研究[J]. 舰船科学技术 , 2015, 37 (8) :165–168.
ZHU Xiao-hong, LI Hai-dong, ZHANG Wei-dong. Numerical studies on heat transfer and flow of membrane spiral-tube marine heat exchanger[J]. Ship Science and Technology , 2015, 37 (8) :165–168. |
| [5] | ZHAO T S, BI Q C. Pressure drop characteristics of gas-liquid two-phase flow in vertical miniature triangular channels[J]. International Journal of Heat and Mass Transfer , 2001, 44 (13) :2523–2534. DOI:10.1016/S0017-9310(00)00282-9 |
| [6] |
李冠球. 板式换热器传热传质实验与理论研究[D]. 杭州:浙江大学, 2012.
LI Guan-qiu. Experimental and theoretical investigation of heat and mass transfer in plate heat exchanger[D]. Hangzhou:Zhejiang University, 2012. |
| [7] |
吴嘉峰. 微通道流动冷凝流型和传热机理的研究[D]. 南京:东南大学, 2009.
WU Jia-feng. The research of flow pattern and heat transfer mechanism of micro channel flow[D]. Nanjing:Southeast University, 2009. |
| [8] |
杨玉顺.
工程热力学[M]. 北京: 机械工业出版社, 2009 .
YANG Yu-shun. Engineering thermodynamics[M]. Beijing: China Machine Industry Press, 2009 . |
| [9] |
杨世铭, 陶文铨.
传热学[M]. 北京: 高等教育出版社, 2010 .
YANG Shi-ming, TAO Wen-quan. Heat transfer theory[M]. Beijing: Higher Education Press, 2010 . |
| [10] | AKERS W W, DEANS H A, CROSSER O K. Condensation heat transfer within horizontal tubes[J]. Chemical Engineering Progress Symposium Series , 1959, 55 (29) :171–176. |
| [11] | DEBRAY F, FRANC J P, MAITRE T, et al. Mesure des coefficients de transfert thermique par convection forcée en mini-canaux[J]. Mécanique & Industries , 2001, 2 (5) :443–454. |
 2016, Vol. 38
2016, Vol. 38
