系统辨识与自航模试验相结合的系统辨识方法在近年来得到广泛研究,用以对海洋运载器进行动力学建模。近几十年以来,提出了多种系统辨识算法,传统的辨识方法包括最小二乘法、卡尔曼滤波法、预报误差法等。然而,对初值的依赖性是这些传统方法的一大缺陷,并限制了其应用。因此,一些不依赖于初值的新型辨识方法得以提出,包括频域辨识法、人工神经网络和支持向量机(Support Vector Machines,SVM)。
支持向量机首先由 Vapnik 于 20 世纪 90 年代提出,它基于结构风险最小化原则,主要用于处理小样本问题,在解决分类和回归问题方面具有良好性能,已在模式识别、控制应用和系统辨识等领域得到广泛应用。罗伟林等[1]首先使用最小二乘支持向量机(Least Square SVM,LS-SVM)对船舶操纵运动进行辨识建模,对 Abkowitz 模型中的水动力导数进行辨识,随后张心光等[2]使用 ε-SVM 完成了相同的工作,徐锋等[3]使用最小二乘支持向量机对水下航行器的非线性动力学进行了辨识建模研究。
虽然支持向量机通常用来处理离线的批处理问题,但实际上也可用于处理参数的在线辨识问题。常用的在线算法包括增量式最小二乘支持向量机和滑动窗模式的最小二乘支持向量机。由于最小二乘支持向量机的求解可以转换为线性方程组,在线最小二乘支持向量机可以通过核函数矩阵的转换进行推导。徐锋等使用增量式最小二乘法对船舶和水下航行器的水动力导数进行辨识[4-5],刘胜等[6]使用滑动窗模式的最小二乘支持向量机对船舶横摇运动进行建模。
本文以 MARIUS AUV 为研究对象,使用增量式最小二乘支持向量机对其水动力导数进行在线辨识。首先,通过约束模试验和经验公式对其数学模型中的水动力导数进行计算,基于这些水动力导数进行操纵运动仿真以获取样本数据。然后,基于积分型辨识样本结构构造输入输出样本对。最后,对最小二乘支持向量机进行推导,并用来对样本数据进行分析和水动力导数的在线辨识。
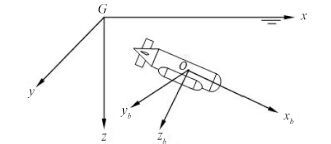
1 MARIUS AUV 的操纵运动数学模型为描述水下航行器的运动特征,需要建立 2 个参考坐标系。一个是惯性坐标系 G-xyz,另一个是运动坐标系 O-xbybzb。2 个坐标系如图 1 所示。
|
图 1 水下航行器的坐标系统 Fig. 1 Coordinate systems for underwater vehicles in maneuvering motion |
通常情况下,需要考虑水下航行器的六自由度运动,但在弱机动条件下,水下航行器的六自由度运动可以分解为水平面运动和垂直面运动。本文仅考虑水平面运动。基于刚体动力学,水面运动的动力学方程可表示为:
| $ \left\{ \begin{array}{l} m(\dot u-vr-{y_G}\dot r-{x_G}{r^2}) = {X_H} + {X_P}{\rm{ + }}{X_{\delta r}} \text{,} \\[5pt] m(\dot v + ur + {x_G}\dot r-{y_G}{r^2}) = {Y_H} + {Y_P} + {Y_{\delta r}} \text{,} \\[5pt] {I_z}\dot r \!+\! m\left[{{x_G}(\dot v \!+\! ur) \!-\!{y_G}(\dot u-vr)} \right] \!=\! {N_H} \!+ \!{N_P}\! + \!{N_{\delta r}} \text{。} \end{array} \right. $ | (1) |
其中:m 为水下航行器的质量;Iz 为惯性矩;xG,yG为重心坐标;XH,YH,NH 为作用于艇体的流体动力和力矩;XP,YP,NP 为螺旋桨的推力和力矩;
其运动方程可表示为:
| $ \left\{ \begin{array}{l} \dot x = u\cos \psi + v\sin \psi \text{,} \\[5pt] \dot y = v\cos \psi-u\sin \psi \text{,} \\[5pt] \dot \psi = r \text{。} \end{array} \right. $ | (2) |
式中:Ψ 为首摇角。
流体动力和力矩通过泰勒级数展开,对 MARIUS AUV,流体动力和力矩 XH,YH,NH 可表述如下[8]:
| $ \begin{array}{l} {X_H} \!\!=\!\! \displaystyle\frac{\rho }{2}{L^3}{{X{'}}_{\dot u}}\dot u \!\!+\!\! \displaystyle\frac{\rho }{2}{L^2}\left( {{{X{'}}_{uu}}{u^2} \!\!+\!\! {{X{'}}_{vv}}{v^2}} \right) \!+\! \displaystyle\frac{\rho }{2}{L^4}{{X{'}}_{rr}}{r^2}{\rm{ \!\!+\!\! }}\displaystyle\frac{\rho }{2}{L^3}{{X{'}}_{vr}}vr \text{,} \\[10pt] {Y_H} \!\! = \!\! \displaystyle\frac{\rho }{2}{L^3}{{Y{'}}_r}ur \!\! + \!\! \displaystyle\frac{\rho }{2}{L^2}{{Y{'}}_v}uv + \displaystyle\frac{\rho }{{2u}}{L^5}{{Y{'}}_{rrr}}{r^3} +\displaystyle \frac{\rho }{2}{L^4}{{Y{'}}_{r\left| r \right|}}r\left| r \right| + \\[10pt] \;\;\;\;\;\;\; \displaystyle\frac{\rho }{2}{L^2}{{Y{'}}_{v\left| v \right|}}v\left| v \right| + \displaystyle\frac{\rho }{2}{L^3}{{Y{'}}_{\dot v}}\dot v + \displaystyle\frac{\rho }{2}{L^4}{Y_{\dot r}}^\prime \dot r \text{,} \\[10pt] {N_H} \!\! = \!\! \displaystyle\frac{\rho }{2}{L^4}{{N{'}}_r}ur \! + \! \displaystyle\frac{\rho }{2}{L^3}{{N{'}}_v}uv \! + \! \displaystyle\frac{\rho }{{2u}}{L^6}{{N{'}}_{rrr}}{r^3} + \displaystyle\frac{\rho }{2}{L^5}{{N{'}}_{r\left| r \right|}}r\left| r \right| + \\[10pt] \;\;\;\;\;\;\;\; \displaystyle\frac{\rho }{2}{L^3}{{N{'}}_{v\left| v \right|}}v\left| v \right| + \displaystyle\frac{\rho }{2}{L^4}{{N{'}}_{\dot v}}\dot v + \displaystyle\frac{\rho }{2}{L^5}{{N{'}}_{\dot r}}\dot r \text{。} \end{array} $ | (3) |
舵力和力矩可表述如下[8]:
| $ \begin{aligned} {X_{\delta r}} = & \frac{\rho }{2}{L^2}{u^2}{X{'}_{\delta r\delta r}}\delta _r^2\;{Y_{\delta r}} = \\ & \frac{\rho }{2}{L^2}{u^2}{Y{'}_{\delta r}}\delta _r^{}\;{N_{\delta r}} \!=\! \frac{\rho }{2}{L^2}{u^2}{N{'}_{\delta r}}\delta _r^{} \text{,} \end{aligned} $ | (4) |
基于文献 [8],螺旋桨的推力模型如下:
| $ {X_p} = \frac{1}{2}\rho {L^2}{u^2}{X{'}_p} \text{。} $ | (5) |
式中:
为执行操纵运动仿真,需要获取所有的水动力导数。文献 [8] 基于约束模试验给出了部分水动力导数,剩余的水动力导数包括 Y'r|r| 和 N'r|r| 可通过经验公式估算。基于文献 [9] 给出的估算公式计算如下:
| $ {Y{'}_{r\left| r \right|}} =-\frac{{{F_2}}}{{{L^2}{F_0}}}{Y{'}_{v\left| v \right|}},\;\;{N{'}_{r\left| r \right|}} =-\frac{{{F_3}}}{{{L^2}{F_2}}}{Y{'}_{v\left| v \right|}} \text{。} $ | (6) |
式中:F0,F2和 F3分别为纵剖面关于 Z 轴的 0 阶、2 阶和,3 阶静矩;L 为艇体长度。
MARIUS AUV 的物理参数和水动力导数分别如表 1 和表 2 所示。
|
|
表 1 MARIUS AUV 的物理参数 Tab.1 Physical parameters of MARIUS vehicle |
|
|
表 2 MARIUS AUV 的水动力导数(×10-5) Tab.2 Hydrodynamic derivatives of MARIUS AUV(×10-5) |
支持向量机包括标准型和改进型,最小二乘支持向量机即是改进型的一种。在本节将通过核函数矩阵的递推对增量式最小二乘支持向量机进行推导。
对于给定的输入输出样本集[x,y],最小二乘支持向量机可以转化为求解以下线性方程组[1-3]:
| $ \left[\begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\overrightarrow 1 \\ {\overrightarrow 1 ^{\rm{T}}}\;\;\;\varOmega + {C^{-1}}I \end{array} \right]\left[\begin{array}{l} b\\ \alpha \end{array} \right] = \left[\begin{array}{l} \overrightarrow 0 \\ y \end{array} \right] \text{。} $ | (7) |
式中:
在求解式(7)后,可得到回归公式如下:
| $ y(x) = \sum\limits_{i = 1}^n {{\alpha _i}K} ({x_i},x) + b \text{。} $ | (8) |
对于参数辨识问题,通常采用线性核函数,即 K(x,x')=(x·x')。
对于增量式最小二乘支持向量机,辨识样本随着时间递增。随着时间的更新,每次增加在样本集{x,y}中加入一个新的样本。因此,样本集可以表示为时间步 t 的函数,即{x(t),y(t)},其中,x(t)=[x1,x2,…,xt],y(t)=[y1,y2,…,yt],核函数矩阵 Ω、拉格朗日乘数 α 和偏置 b 均可表示为时间 t 的函数,可表述如下:
| $ \begin{aligned} { \varOmega} (i,j) = & K({x_i},{x_j}),\;\;i,j = 1,2,\cdots ,t,\;\;\;\alpha (t) = \\ & {({\alpha _1},{\alpha _2},\cdots {\alpha _t})^{]rm T}},\;\;\;b(t) = {b_t}\text{。} \end{aligned} $ |
重写式(8)如下:
| $ y(x,t) = \sum\limits_{i = 1}^t {{\alpha _i}(t)K({x_i},x)} + b(t) \text{,} $ | (9) |
假设Γ(t)=Ω/t+C-1I,同时考虑到 e 也随着时间变化,式(7)可表示为:
| $ \left[\begin{gathered} 0\;\;\;\;\;\;\;\;e(t) \hfill \\ e{(t)^{\text{T}}}\;\;\Gamma (t) \hfill \\ \end{gathered} \right]\left[\begin{gathered} b(t) \hfill \\ \alpha (t) \hfill \\ \end{gathered} \right] = \left[\begin{gathered} \;\;\overrightarrow 0 \hfill \\ y(t) \hfill \\ \end{gathered} \right] \text{,} $ | (10) |
从式(10)可得到:
| $ {e^{\text{T}}}\alpha (t) = 0 \text{,} $ | (11) |
| $ eb(t) + \varGamma (t)\alpha (t) = y(t) \text{,} $ | (12) |
假设 P(t)=Γ(t)-1,并在式(12)两端同乘以 eTP(t),可以得到:
| $ {e^{\text{T}}}P(t)eb(t) + {e^{\text{T}}}\alpha (t) = {e^{\text{T}}}U(t)y(t) \text{,} $ | (13) |
把式(11)代入式(13)得到:
| $ {e^{\text{T}}}P(t)eb(t) = {e^{\text{T}}}U(t)y(t) \text{,} $ | (14) |
求解式(14)得到:
| $ b(t) = \frac{{{e^{\text{T}}}P(t)y(t)}}{{{e^{\text{T}}}P(t)e}} \text{,} $ | (15) |
把式(15)代入式(12),可得到:
| $ \alpha \left( t \right) = P\left( t \right)\left( {y\left( t \right)-\frac{{e{e^{\text{T}}}P\left( t \right)y\left( t \right)}}{{{e^{\text{T}}}P\left( t \right)e}}} \right) \text{。} $ | (16) |
从式(15)和式(16)不难发现,增量式最小二乘支持向量机的求解关键在于求解 P(t)。如果样本数目足够大,通过求解的逆矩阵以求解 P(t)的难度较大。因此,必须通过矩阵转换理论对 P(t)的求解进行转换。
在 t 时刻,核函数矩阵式 t×t 方阵,表示如下:
| $ {\textstyle{{\varGamma}} \left( t \right) \!\! = \!\! {{{\varOmega}} _t} + {{{C}}^{-1}}I \!\! = \!\! \left[\begin{gathered} k\!\!\left( {{x_1},\!\!{x_1}} \right) \!\!+\!\! {1 \mathord{\left/ {\vphantom {1 {C\; \cdots \;\;\;\;\;\;\;k\left( {{x_t},\;{x_1}} \right)}}} \right. } {C\;\; \cdots \;\;\;k\left( {{x_t},\;{x_1}} \right)}} \hfill \\ \;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\; \vdots \hfill \\ \;k\left( {{x_1},\;{x_1}} \right)\;\;\;\; \cdots \;k\left( {{x_t},\!\!{x_t}} \right) \!\!+\!\! {1 \mathord{\left/ {\vphantom {1 C}} \right. } C} \hfill \\ \end{gathered} \right] \text{,}} $ | (17) |
在时间步 t+1,新样本(xt+1,yt+1)加入样本集,样本数目变为 t+1。因此,Γ(t)变为
| $ {{\varGamma}} \left( {t + 1} \right) = {{{\varOmega}} _{t + 1}} + {{{C}}^{-1}}I = \left[\begin{gathered} k\left( {{x_1},\;{x_1}} \right) + {1 \mathord{\left/ {\vphantom {1 {C\;\; \cdots \;\;\;\;\;\;\;\;k\left( {{x_t},\;{x_1}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k\left( {{x_{t + 1}},\;{x_1}} \right)}}} \right. } {C\;\; \cdots \;\;\;\;\;\;\;\;k\left( {{x_t},\;{x_1}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k\left( {{x_{t + 1}},\;{x_1}} \right)}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \hfill \\ \;\;\;\;k\left( {{x_1},\;{x_1}} \right)\;\;\;\;\;\;\; \cdots \;\;\;\;k\left( {{x_t},\;{x_t}} \right) + {1 \mathord{\left/ {\vphantom {1 {C\;}}} \right. } {C\;}}\;\;\;\;\;\;\;\;\;\;k\left( {{x_{t + 1}},\;{x_t}} \right) \hfill \\ \;\;\;k\left( {{x_1},\;{x_{t + 1}}} \right)\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;k\left( {{x_t},\;{x_{t + 1}}} \right)\;\;\;\;\;\;k\left( {{x_{t + 1}},\;{x_{t + 1}}} \right) + {1 \mathord{\left/ {\vphantom {1 {C\;}}} \right. } {C\;}}\; \hfill \\ \end{gathered} \right] \text{。} $ | (18) |
对比Γ(t)和Γ(t+1),可表示如下:
| $ \varGamma \left( {t + 1} \right) = \left[\begin{gathered} \varGamma \left( t \right)\;\;\;\;\;\;\;\;\;\;W\left( {t + 1} \right) \\ W{\left( {t + 1} \right)^{\rm T}}\;\;\;w\left( {t + 1} \right) \\ \end{gathered} \right]\text{。} $ | (19) |
式中:
对于矩阵 A,如果它可表示为
| $ \begin{aligned} {A} = & {\left[\begin{array}{l} {A_{11}}\;\;E\\ {E^{\rm T}}\;\;d \end{array} \right]^{-1}} = \left[\begin{array}{l} {A_{11}}\;\;0\\ 0\;\;\;\; 0 \end{array} \right] + \left[\begin{array}{l} A_{11}^{-1}{A_{12}}\times\\ \;\;-I \end{array} \right]\\[5pt] & {\left( {d-{E^{\rm T}}A_{11}^{-1}E} \right)^{-1}}\left[{{E^{\rm T}}A_{11}^{-1}\;\;-I} \right] \text{。} \end{aligned} $ | (20) |
结合式(19)和式(20),P(t+1)可以求解如下:
| $ \begin{array}{l} P\left( {t + 1} \right) = \Gamma {\left( {t + 1} \right)^{-1}} = \\ \quad\quad\,{\left[\begin{array}{l} \;\;\;\Gamma \left( t \right)\;\;\;\;\;\;\;\;\;W\left( {t + 1} \right)\\[10pt] W{\left( {t + 1} \right)^T}\;\;\;\;\;w\left( {t + 1} \right) \end{array} \right]^{-1}} \!\!= \left[\begin{array}{l} \Gamma {\left( t \right)^{-1}}\;\;0\\ \;\;\;\;0\;\;\;\;\;0 \end{array} \right] +\\ \quad\,\,\begin{array}{l} \left. {\left[{\begin{array}{*{20}{c}} {\Gamma {{\left( t \right)}^{-1}}W\left( {t + 1} \right)}\\[10pt] {-I} \end{array}} \right.} \right]\left[{w\left( {t + 1} \right)-W{{\left( {t + 1} \right)}^{\rm{T}}}} \right.\\[10pt] \,\,\left. {\Gamma {{\left( t \right)}^{-1}}W\left( {t + 1} \right)} \right]\left[{W{{\left( {t + 1} \right)}^T}\Gamma {{\left( t \right)}^{-1}}-I} \right]\text{。} \end{array} \end{array} $ | (21) |
总结以上推导过程,增量式最小二乘支持向量机算法可表示如下:
步骤 1 设置初始样本数目,t 必须大于 2;
步骤 2 计算 P(t),b(t) 和 α(t),更新时间步 t 到 t+1;
步骤 3 采集新样本(xt+1,yt+1),使用式(21)计算;
步骤 4 基于式(15)和式(16)计算 bt+1和 αt+1;
步骤 5 更新时间步 t 到 t+1,重复步骤 3。
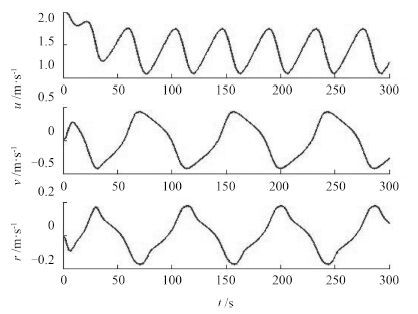
3 结果和分析 3.1 操纵运动仿真为验证提出的参数辨识算法,使用 4 阶龙格库塔法进行 10°/10° Z 形试验的操纵运动仿真。仿真时间步长设置为 0.1 s,仿真时间为 300 s。仿真结果如图 2 所示。
|
图 2 10°/10°Z 形仿真试验 Fig. 2 10°/10° zigzag test in horizontal plane |
设置采样间隔为 0.5 s,可以得到 601 个样本。基于积分型辨识样本结构,可以得到 600 个样本对。输入输出样本对可表示如下[7]:
| $\text{纵向运动}:\text{ }\left\{ \begin{matrix} \text{输入}:\left\{ \begin{matrix} {{u}_{k}}\left| {{u}_{k}} \right|+{{u}_{k+1}}\left| {{u}_{k+1}} \right|,v_{k}^{2}+v_{k+1}^{2},r_{k}^{2}+r_{k+1}^{2},{{v}_{k}}{{r}_{k}}+{{v}_{k+1}}{{r}_{k+1}}, \\ \delta _{r,k+1}^{2}u_{k+1}^{2}+\delta _{r,k+1}^{2}u_{k+1}^{2},\ 1/{{u}_{k+1}}-{{u}_{k+1}}-1/{{u}_{k}}{{u}_{k}} \\ \end{matrix} \right. \\ \text{输出}:\left\{ {{u}_{k+1}}-{{u}_{k}} \right\} \\ \end{matrix} \right.$ |
| $ \text{横向云动}{\text{:}} \left\{ \!\! \begin{gathered} \text{输入}{\text{:}}\left\{ \begin{gathered} {u_k}{r_k} + {u_{k + 1}}{r_{k + 1}},{u_k}{v_k} + {u_{k + 1}}{v_{k + 1}},r_k^3 + r_{k + 1}^3,{r_k}\left| {{r_k}} \right| + {r_{k + 1}}\left| {{r_{k + 1}}} \right|,\hfill \\ {v_k}\left| {{v_k}} \right| + {v_{k + 1}}\left| {{v_{k + 1}}} \right|,{\delta _{r,k}}u_k^2 + {\delta _{r,k + 1}}u_{k + 1}^2 \hfill \\ \end{gathered} \right\} \hfill \\ \text{输出}{\text{:}}\left\{ {{v_{k + 1}}-{v_k}} \right\} \hfill \\ \end{gathered} \right. \text{;} $ |
| $ \text{摇首运动}{\text{:}}\left\{ \!\!\begin{gathered} \text{输入}{\text{:}}\left\{ \begin{gathered} {u_k}{r_k} + {u_{k + 1}}{r_{k + 1}},{u_k}{v_k} + {u_{k + 1}}{v_{k + 1}},r_k^3 + r_{k + 1}^3,{r_k}\left| {{r_k}} \right| + {r_{k + 1}}\left| {{r_{k + 1}}} \right|,\hfill \\ {v_k}\left| {{v_k}} \right| + {v_{k + 1}}\left| {{v_{k + 1}}} \right|,{\delta _{r,k}}u_k^2 + {\delta _{r,k + 1}}u_{k + 1}^2 \hfill \\ \end{gathered} \right\} \hfill \\ \text{输出}{\text{:}}\left\{ {{r_{k + 1}}-{r_k}} \right\} \hfill \\ \end{gathered} \right. \text{;} $ |
基于参数的可辨识性理论[10],惯性水动力导数不参与辨识,可通过理论计算和约束模试验得到。因此,共有 17 个水动力导数参数辨识。
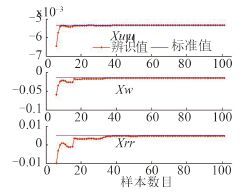
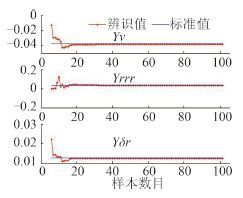
考虑到增量式最小二乘支持向量机在处理小样本数据方面的优越性,从 600 个样本对中等间隔选取 100 个样本对作为辨识样本。在辨识过程中,设置初始样本数目为 5,图 3~图 8 给出了各水动力导数的在线辨识结果。从图中可以看出,当样本数目超过 20 时,所有的水动力导数已经基本收敛于试验值。
|
图 3 Xu∣u∣, Xvv, Xrr 的在线辨识结果 Fig. 3 On-line identification results of Xu∣u∣, Xvv, Xrr |
|
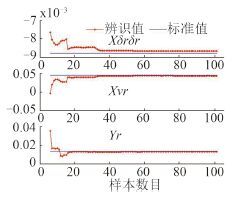
图 4 Xδrδr, Xvr, Yr 的在线辨识结果 Fig. 4 On-line identification results of Xδrδr, Xvr, Yr |
|
图 5 Yv, Yrrr, Yδr 的在线辨识结果 Fig. 5 On-line identification results of Yv, Yrrr, Yδr |
|
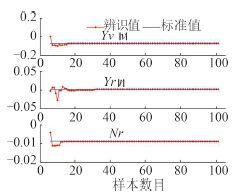
图 6 Yv∣v∣, Xr∣r∣, Nr 的在线辨识结果 Fig. 6 On-line identification results of Yv∣v∣, Xr∣r∣, Nr |
|
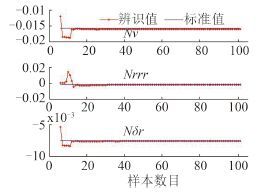
图 7 Nv, Nrrr, Nδr 的在线辨识结果 Fig. 7 On-line identification results of Nv, Nrrr, Nδr |
|
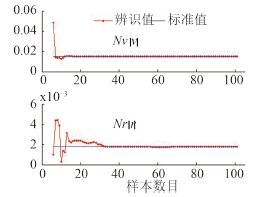
图 8 Nv∣v∣, Nr∣r∣的在线辨识结果 Fig. 8 On-line identification results of Nv∣v∣, Nr∣r∣ |
本文以 MARIUS AUV 为研究对象,对其水平面操纵运动中的水动力导数进行了在线辨识。使用新型的积分型辨识样本结构进行了样本对的构造,辨识得到的水动力导数均能很好的收敛于试验值。这表明所提出的增量式最小二乘支持向量机和积分型辨识样本结构的有效性。本方法可应用于水下航行器操纵运动的精确建模。
| [1] | LUO Wei-lin, ZOU Zao-jian. Identification of response models of ship maneuvering motion using support vector machines[J]. Journal of Ship Mechanics , 2007, 11 (6) :832–838. |
| [2] | ZHANG Xin-guang, ZOU Zao-jian. Identification of Abkowitz model for ship manoeuvring motion using ε-support vector regression[J]. Journal of Ship Mechanics , 2011, 23 (3) :353–360. |
| [3] | XU Feng, ZOU Zao-jian, YIN Jian-chuan, et al. Identification modeling of underwater vehicles' nonlinear dynamics based on support vector machines[J]. Ocean Engineering , 2013, 67 :68–76. DOI:10.1016/j.oceaneng.2013.02.006 |
| [4] | XU Feng, ZOU Zao-jian, YIN Jian-chuan. On-line modeling of ship maneuvering motion based on support vector machines[J]. Journal of Ship Mechanics , 2012, 16 (3) :218–225. |
| [5] | XU Feng, ZOU Zao-jian, YIN Jian-chuan. On-line modeling of AUV's maneuvering motion in diving plane based on SVM[C].//Proceedings of the Twenty-second (2012) International Offshore and Polar Engineering Conference, 2012, (6) 17-22. |
| [6] | 刘胜, 杨震. 船舶横摇运动实时在线预报方法[J]. 电机与控制学报 , 2011, 15 (10) :82–8794. |
| [7] | XU Feng, CHEN Qing, ZOU Zao-jian, et al. Modeling of underwater vehicles' maneuvering motion by using integral sample structure for identification[J]. Journal of Ship Hydrodynamics , 2013, 18 (3) :211–220. |
| [8] | SILVESTRE C, PASCOAL A. Control of an AUV in the vertical and horizontal planes:system design and tests at sea[J]. Transactions of the Institute of Measurement and Control , 1997, 19 (3) :126–138. DOI:10.1177/014233129701900303 |
| [9] | 施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995 . |
| [10] | 罗伟林, 李铁山, 邹早建. 船舶操纵运动建模中的参数可辨识性问题[J]. 大连海事大学学报 , 2009, 35 (4) :1–3. |
 2016, Vol. 38
2016, Vol. 38
