对于民用船舶,振动与噪声直接影响到船员的舒适性及机械设备的疲劳寿命,对于军用舰船或潜艇,则直接影响到隐蔽性和作战性能。隔振是降低机械设备通过基座传递结构噪声的主要手段,舰船、潜艇等的动力机械设备大多是通过弹性支撑,如金属橡胶隔振器安装在弹性甲板或柔性梁板等非刚性基础上,以对振源激励向柔性基础结构的传递进行隔离。传统隔振分析中常把甲板等安装基础视作刚体[1],但实际上基础的刚度和质量均有限,这样的简化会一定程度上影响到隔振设计和效果,特别是在基础板耦合共振阶段。
评价隔振效果的指标主要包括力传递率、振级落差、插入损失和功率流传递率等,其中功率流将传递力和响应集中考虑,摆脱了力传递率和振级落差在效果评估上顾此失彼的局面,因此,功率流评估方法已成为分析柔性基础隔振的重要工具[2-4]。
目前常见的对柔性基础隔振分析的方法有理论、实验和仿真等方法。童宗鹏等[5]对带泵组浮筏隔振装置的潜艇舱段建立有限元模型以分析各系统参数对隔振特性的影响,并做了舱段缩比模型水下试验验证,但该方法仅仅研究了一个特例,并未从理论上探寻柔性隔振的普遍规律;程广利等[6]对基础分别为固定刚体、悬浮刚体和漂浮刚体等情况的隔振效率进行研究,分析了 3 种情况对隔振效果的影响,但该模型并未涉及基础本身的变形及振动耦合;李玉龙等[7]运用 ADAMS 软件与有限元软件结合,仿真了柔性基础上金属橡胶隔振器的隔振情况,分析了不同参数对系统隔振性能的影响,但阻尼等计算参数或边界条件难以确定,限制了单纯的数值仿真的准确度;此外,行晓亮等[8]通过电-力-声类比方法,建立了浮筏系统理论模型,并采用了导纳形式的功率流方法对该模型进行分析。
为进一步探寻柔性基础隔振规律,建立了圆形柔性基础板-隔振器-机械设备的刚柔耦合隔振模型,根据谐波平衡原理得到系统受到简谐外激力时的基于贝塞尔函数的响应,推导出通过隔振器传入到柔性基础的功率流或基础的平均总动能,并以此为评价指标讨论了设备质量、隔振器刚度和阻尼、柔性基础刚度和阻尼等参数对隔振系统隔振能力的影响,以期为柔性基础隔振优化设计提供参考。
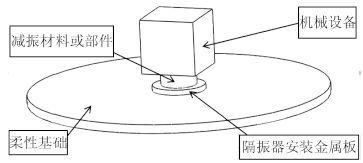
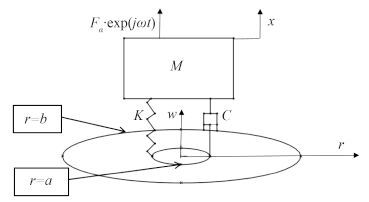
1 柔性圆板基础上隔振系统的数学模型 1.1 模型描述 图 1 是设备通过减振器安装在圆形柔性基础上的示意图,减振器通过其安装金属面板焊接或通过螺栓安装在基础板上。为对该模型进行理论分析,将其简化为图 2 所示的模型,仅考虑能自由做横向振动的底板,将其简化为内、外径为 a、b 的穿孔板,板厚为 h;由于几何、边界和激励等的对称性,横向振动的位移仅与半径 r 有关;外径处设为简支边界;考虑到减振器安装金属板刚度较大,内径处边界条件为径向转角为 0,剪力与隔振器的作用力平衡。对于振动问题,由于其振幅不大,可将减振器简化为刚度系数为 K,阻尼系数为的线性元件 C。机械设备看成集中质量 M,并有外激励
|
图 1 机械设备安装示意图 Fig. 1 Sketch map of mechanical device installation |
|
图 2 柔性基础隔振模型 Fig. 2 Model of vibration isolation system with flexible foundation |
为进一步描述和求解该模型,建立单自由度 Ox 坐标以描述机械设备 M 的运动,建立坐标系 Orw 描述柔性基础板的运动,其中
基础板振动满足振动方程:
| $ \frac{{E{h^2}}}{{12\rho (1-{\mu ^2})}}{\nabla ^4}w + \frac{{{\partial ^2}w}}{{\partial {t^2}}} = 0 \text{。} $ | (1) |
机械设备 M 的运动满足以下方程:
| $ M\ddot x{\rm{ + }}C(\dot x-\dot w(a,t)) + K(x-w(a,t)) = {F_a} \cdot {e^{j\omega t}} \text{。} $ | (2) |
隔振器的作用力为:
| $ f = {f_a}{e^{j\omega t}} = C(\dot x-\dot w(a,t)) + K(x-w(a,t)) \text{。} $ | (3) |
采用分离变量法,令
| $ {\nabla ^4}{w_a} = {k^4}{w_a} \text{,} $ | (4) |
即
| $ ({\nabla ^2} + {k^2})({\nabla ^2}-{k^2}){w_a} = 0 \text{。} $ | (5) |
因此方程(5)的解可表示为 waⅠ 和 waⅡ 的线性组合,waⅠ 和 waⅡ 分别满足下列方程:
| $ ({\nabla ^2} + {k^2}){w_a}^{\rm I} = 0 \text{,} $ | (6) |
| $ ({\nabla ^2}-{k^2}){w_a}^{{\rm I}{\rm I}} = 0 \text{。} $ | (7) |
由于基础板是圆形的,采用极坐标形式,并考虑极轴对称,将式(6)和式(7)改写成:
| $ ({{{d^2}} \over {d{r^2}}} + {1 \over r}{d \over {dr}} + {k^2}){w_a}^{\rm I} = 0 \text{,} $ | (8) |
| $ ({{{d^2}} \over {d{r^2}}} + {1 \over r}{d \over {dr}}-{k^2}){w_a}^{{\rm I}{\rm I}} = 0 \text{。} $ | (9) |
方程(8)为零阶柱贝塞尔方程,其解可表示为:
| $ {w_a}^{\rm I} = A{J_0}(kr) + B{N_0}(kr) \text{。} $ | (10) |
式中:A,B 为系数;J0(r),N0(r)分别为 0 阶柱贝塞尔函数和零阶柱诺依曼函数。
方程(9)为零阶虚宗量柱贝塞尔方程,其解可表示为:
| $ {w_a}^{ I} = G{I_0}(kr) + H{K_0}(kr) \text{。} $ | (11) |
其中,G,H 为系数;I0(r),K0(r)分别为零阶虚宗量柱贝塞尔函数和零阶虚宗量柱诺依曼函数。
wa 可表示为:
| $ {w_a}^{} = A{J_0}(kr) + B{N_0}(kr) + G{I_0}(kr) + H{K_0}(kr) \text{。} $ | (12) |
在外径 r=b 处,位移和弯矩为 0,即
| $ {w_a}(b) = 0 \text{,} $ | (13) |
| $ {M_r}\left| {_{r = b}} \right. =-D({{{d^2}{w_a}} \over {d{r^2}}} + \mu {1 \over r}{{d{w_a}} \over {dr}})\left| {_{r = b}} \right. = 0 \text{。} $ | (14) |
其中
在内径 r=a 处,径向转角为 0,横向剪力与减振器内力平衡,即
| $ {{\partial {w_a}} \over {\partial r}}\left| {_{r = a}} \right. = 0 \text{,} $ | (15) |
| $ {Q_r} =-D\frac{d}{{dr}}({\nabla ^2}{w_a}) =-{{{f_a}} \mathord{\left/ {\vphantom {{{f_a}} {2{\rm{\pi }}a}}} \right. } {2{\rm{\pi }}a}} \text{。} $ | (16) |
将式(12)代入式(13)~式(16),可得
| $ A{J_0}(kb) + B{N_0}(kb) + G{I_0}(kb) + H{K_0}(kb) = 0 \text{,} $ | (17) |
| $ \begin{array}{l} A\left[{-{k^2}{J_0}(kb)-k\displaystyle\frac{{\mu-1}}{b}{J_1}(kb)} \right]+\\ [8pt] B\left[{-{k^2}{N_0}(kb)-k\displaystyle\frac{{\mu-1}}{b}{N_1}(kb)} \right]+\\ [8pt] G\left[{{k^2}{I_0}(kb) + k \displaystyle\frac{{\mu-1}}{b}{I_1}(kb)} \right]+\\ [8pt] H\left[{{k^2}{K_0}(kb)-k\displaystyle\frac{{\mu-1}}{b}{K_1}(kb)} \right] = 0 \text{,} \end{array} $ | (18) |
| $ \begin{aligned} A\left[{-k{J_1}(ka)} \right] + & B\left[{-k{N_1}(ka)} \right] + G\left[{k{I_1}(ka)} \right] + \\ & H\left[{-k{K_1}(ka)} \right] \!\!=\!\! 0 \text{。} \end{aligned} $ | (19) |
| $ \begin{aligned} A\left[{{k^3}{J_1}(ka)} \right] + & B\left[{{k^3}{N_1}(ka)} \right] + G\left[{{k^3}{I_1}(ka)} \right] + \\ & H\left[{-{k^3}{K_1}(ka)} \right] = {f \mathord{\left/ {\vphantom {f {2\pi aD}}} \right. } {2\pi aD}} \text{。} \end{aligned} $ | (20) |
解线性方程组(17)~(20)可得 A,B,G 和 H,代入式(12)得到 wa。
记基础板内径处输入位移阻抗为:
| $ Z = {{{f_a}} \over {{w_a}(a)}} \text{。} $ | (21) |
考虑到基础板的阻尼,即 E = EI + EII
根据谐波平衡原理,由外激励为
| $ {x_a} = {{{F_a}} \over {{Z_x}}} \text{,} $ $ {Z_x} =-M{\omega ^2} + Z{{K + jC\omega } \over {Z + K + jC\omega }} \text{,} $ | (22) |
其中:
| $ {Z_x} =-M{\omega ^2} + Z{{K + jC\omega } \over {Z + K + jC\omega }} \text{。} $ | (24) |
从而求得系统在外激励
以通过隔振器传递到基础板的功率流为评价指标来评价各因素对整个系统的隔振效率的影响;但当考虑基础板阻尼时,传递到基础板的功率流并不能直接反应基础板的振动强度,为此,本文采用基础板平均总动能来衡量隔振系统的隔振效率。
2.1 传递到基础板的功率流传递到基础板的瞬时功率流为:
| $ {P_i} = f \cdot \dot w(a,t) \text{,} $ | (25) |
平均功率流为:
| $ {\bar P_i} = {1 \over T}\int_0^T {{P_i}} {\text{d}}t \text{。} $ | (26) |
其中 T=2π/
取圆板上(r,r+dr)的一个面元,则该面元质量为 2πrdr·h,其平均振动动能为:
| $ d{E_k} = {1 \over T}\int_0^T {{1 \over 2}} (2\pi rdr \cdot h\rho ){({{dw(r,t)} \over {{\text{d}}t}})^2}{\text{d}}t \text{,} $ | (27) |
则整个圆板的平均总动能为:
| $ {E_k} = \int_a^b {{\text{d}}{E_k}} \text{。} $ | (28) |
将式(12)和式(27)代入式(28)可求得基础板的平均总动能 Ek[10]。
3 频谱分析设定相关参数,并按上一节中方法求解传入基础板的功率流或基础板总动能,并对结果进行分析。
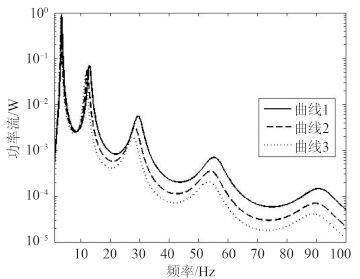
3.1 设备质量的影响图 3 是机械设备质量取值不同时得到的功率流曲线,其中曲线 1 ~ 曲线 3 对应的设备质量依次递增,从图中可以看出,功率流曲线随频率增加而发生波动,交替呈现出多个峰值与谷值,变化规律较复杂,这由柔性基础的耦合作用引起。在绝大部分频段内,随着设备质量的增加,传递到柔性基础上的功率流逐渐减小。
|
图 3 不同设备质量下的功率流曲线 Fig. 3 Power flow curves with different equipment mass |
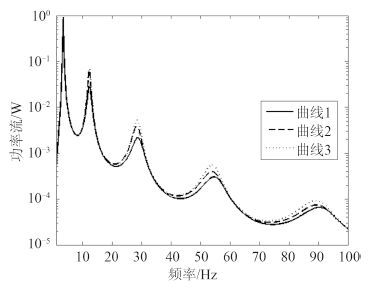
图 4 是隔振器刚度取值不同时得到的功率流曲线,其中曲线 1 ~ 曲线 3 对应的隔振器刚度依次递增,从图中可看出,在绝大部分频段内,随着隔振器刚度的增加,传递到柔性基础上的功率流逐渐增大。
|
图 4 不同隔振器刚度下的功率流曲线 Fig. 4 Power flow curves with different isolator stiffness |
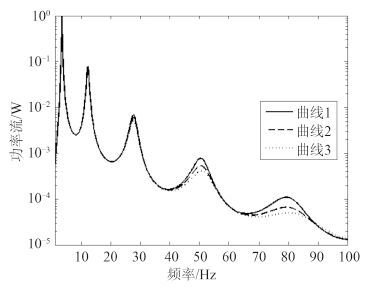
图 5 是隔振器阻尼取值不同时得到的功率流曲线,其中曲线 1、曲线 2、曲线 3 对应的隔振器阻尼依次递增。从图中可看出,阻尼主要是在共振峰值附近起作用,在非共振频段,阻尼影响不大。随着隔振器阻尼的增加,传递到柔性基础上的功率流也随之增大。
|
图 5 不同隔振器阻尼下的功率流曲线 Fig. 5 Power flow curves with different isolator damping |
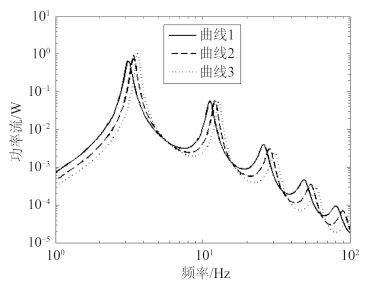
图 6 是基础板刚度取值不同时得到的功率流曲线,其中曲线 1 ~ 曲线 3 对应的基础板刚度依次递增。从图中可看出,基础板刚度对隔振系统共振频率有直接影响,基础板刚度越大,共振频率越大,反之亦然。在大部分频段,随着基础板刚度的增加,传递到柔性基础上的功率流逐渐减小,较大的基础板刚度有利于隔振设计,但需注意并非在所有频段上都如此。
|
图 6 不同基础刚度下的功率流曲线 Fig. 6 Power flow curves with different foundation stiffness |
当考虑到基础板阻尼时,由隔振器传递到基础板的能量一部分会被基础板材料阻尼消耗掉,剩下的才是基础板振动所具有的能量,因此,仅用传递到基础板的功率流来衡量隔振系统隔振效率并不准确。为了更准确描述基础板的振动强度,本文采用基础板平均总动能作为评价隔振系统效率的指标。
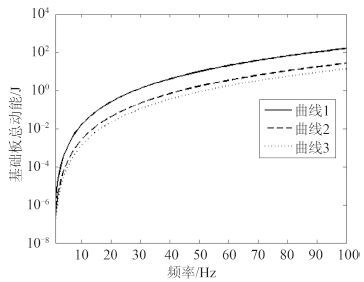
图 7 是基础板阻尼取值不同时得到的基础板平均总动能(以下简称总动能)曲线,其中曲线 1 ~ 曲线 3 对应的基础板阻尼依次递增。从图中可看出,随着振动频率的增加,总动能也随之增加。随着基础板阻尼的增加,总动能逐渐降低,可见,增大基础板阻尼有利于隔振设计。
|
图 7 不同基础阻尼下的功率流曲线 Fig. 7 Power flow curves with different foundation damping |
通过建立由柔性基础板、隔振器及机械设备组成的耦合系统的模型,并分析了设备质量、隔振器刚度及阻尼、柔性基础刚度及阻尼等参数对隔振系统隔振效率的影响,由各计算曲线分析可得以下结论:
1)机械设备的质量越大,传递到柔性基础的能量越小,对系统隔振越有利;
2)隔振器刚度越大,传递到柔性基础的能量越大,对隔振设计不利,应在保证静力要求的前提下合理降低隔振器的刚度;
3)隔振器阻尼越大,传递到柔性基础的能量越小,对系统隔振越有利,且隔振器阻尼主要在系统固有频率附近起作用,能有效抑制共振处峰值;
4)在大部分频段,基础板刚度越大,传递到柔性基础上的能量越小,适当增加基础板刚度有利于隔振设计,但并非在所有频段上都如此,因此在隔振设计时,应充分考虑外激励频率与基础板柔性的影响;
5)基础板阻尼越大,其总振动能量越小,越有利于隔振设计。
| [1] |
孙玲玲, 宋孔杰. 柴油机多支承隔振系统的功率流特性[J]. 内燃机学报 , 2003, 21 (4) :249–252.
SUN Ling-ling, SONG Kong-jie. Power flow characteristics of flexible isolation system with multiple mountings[J]. Transactions of CSICE , 2003, 21 (4) :249–252. |
| [2] |
关珊珊, 陈美霞, 陈乐佳, 等. 基于有限元动力计算的浮筏隔振系统功率流研究[J]. 舰船科学技术 , 2007, 29 (5) :132–135.
GUAN Shan-shan, CHEN Mei-xia, CHEN Le-jia, et al. Investigation of power flow in a floating raft isolating system based on finite element dynamic analysis[J]. Ship Science and Technology , 2007, 29 (5) :132–135. |
| [3] | XIONG Y P, XING J T, PRICE W G. Interactive power flow characteristics of an integrated equipment-nonlinear isolator-travelling flexible ship excited by sea waves[J]. Journal of Sound and Vibration , 2005, 287 (1/2) :245–276. |
| [4] |
邓海华. 整舱浮筏功率流测试初步分析研究[J]. 舰船科学技术 , 2006, 28 (S2) :81–85.
DENG Hai-hua. Research of power flow in the-whole-cabin-floating raft vibration isolation[J]. Ship Science and Technology , 2006, 28 (S2) :81–85. |
| [5] |
童宗鹏, 章艺, 尚国清, 等. 舱筏隔振系统水下振动特性的理论分析与试验研究[J]. 振动与冲击 , 2005, 24 (6) :71–74.
TONG Zong-peng, ZHANG Yi, SHANG Guo-qing, et al. Theoretical and experimental research on the vibration of cabin with floating raft isolation system[J]. Journal of Vibration and Shock , 2005, 24 (6) :71–74. |
| [6] |
程广利, 伍先俊, 朱石坚, 等. 船舶的不同基础状态对隔振效率的影响[J]. 舰船科学技术 , 2005, 27 (1) :21–23.
CHENG Guang-li, WU Xian-jun, ZHU Shi-jian, et al. The influences on vibration insulation efficiency for ship under some base situations[J]. Ship Science and Technology , 2005, 27 (1) :21–23. |
| [7] |
李玉龙, 白鸿柏, 何忠波, 等. 柔性基础上金属橡胶非线性隔振系统性能分析[J]. 机械科学与技术 , 2015, 34 (1) :42–46.
LI Yu-long, BAI Hong-bai, HE Zhong-bo, et al. Study on the performance of nonlinear metal-rubber isolation system on flexible base[J]. Mechanical Science and Technology for Aerospace Engineering , 2015, 34 (1) :42–46. |
| [8] |
行晓亮, 王敏庆, 宋代科. 弹性基础浮筏的导纳功率流研究[J]. 机械科学与技术 , 2005, 24 (7) :761–763.
XING Xiao-liang, WANG Min-qing, SONG Dai-ke. Study on vibration characteristic of flexible-basement floating raft vibration-isolation system[J]. Mechanical Science and Technology , 2005, 24 (7) :761–763. |
| [9] |
朱石坚, 何琳.
船舶机械振动控制[M]. 北京: 国防工业出版社, 2006 .
ZHU Shi-jian, HE Ling. Vibration control of onboard machinery[M]. Beijing: National Defense Industry Press, 2006 . |
| [10] |
杜功焕, 朱哲民, 龚秀芬.
声学基础[M]. 3版. 南京: 南京大学出版社, 2012 .
DU Gong-huan, ZHU Zhe-min, GONG Xiu-fen. Fundamentals of acoustics[M]. 3rd ed. Nanjing: Nanjing University Press, 2012 . |
 2016, Vol. 38
2016, Vol. 38
