2. 大连舰艇学院, 辽宁 大连 116018
2. Dalian Naval Academy, Dalian 116018, China
船舶摇荡预报对于舰载机安全起降等有重要意义。根据舰载机安全起降对船舶横摇、纵摇、垂荡等要求,采用极短时间预报方法找出未来一段时间内符合着舰要求的时间窗口,使指挥官能够在舰载机准备下滑或正在下滑时及时向飞行员通报船体摇荡情况,可以为舰载机起降作业提供一定的辅助决策支持 [1]。
目前在船舶摇荡预报方面,国内研究单位主要有哈尔滨工程大学、大连舰艇学院和中船重工集团第 702 研究所等单位[1]。哈尔滨工程大学采用的主要预报方法包括自回归法[2]、最小二乘法[3]、首前波法、卡尔曼滤波法、周期图法、投影寻踪法及神经网络方法[4]等,主要对船模实验摇荡数据进行预报。大连舰艇学院主要采用混沌时间序列分析方法进行预报[5]。702 研究所主要用 ARMA 模型和神经网络模型进行预报。在已查阅的国内外相关资料之中,还未发现对实船测试数据的有效预报达到 15 s 的文献和研究成果。
本文结合实测的船舶摇荡数据,采用回声状态网络方法进行连续极短期预报。
1 船舶摇荡数据的采集与分析 1.1 实验设备介绍为测量船舶的运动姿态,分别采用膜电位水平传感器、运动姿态测量产品 VM-i 进行测量[6]。
膜电位传感器通过串口将数据读入计算机,由数据采集卡自动采集,输出数据结构为:序号、横摇、纵摇。VMESENS VM-i 数据输出结构为:首摇,纵摇,横摇,X 轴磁场强度,y 轴磁场强度,Z 轴磁场强度,X 轴陀螺仪输出,Y 轴陀螺仪输出,Z 轴陀螺仪输出,X 轴加速度,Y 轴加速度,Z 轴加速度。
1.2 实验概况采用膜电位传感器和 VM-i 分别对某船和某实习训练船的摇荡情况进行测量,第 1 次测量时间从 2011 年 6 月 12 日-6 月 17 日,测量对象为某船,测量海域为黄海。第 2 次为某实习训练船出国访问时随船测量,时间从 2011 年 8 月 2 日-8 月 12 日,测量海域分别为海参崴到元山段以及元山到旅顺段[7]。

|
图 1 测姿实验现场 Fig. 1 Motion measurement equipment |
回声状态网络(ESNs) 是 2001 年由德国 Bremen 大学的 Jaeger 教授提出的一种新型的神经网络,是递归神经网络的一种,其结构与生物神经网络非常类似。2004 年 Jaeger 教授将该网络用于麦克格拉斯混沌时间序列的预测,使其预测精度提高了 2 400 倍,得到了极大的关注。
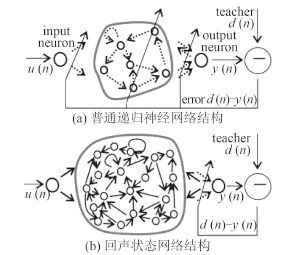
相对普通的递归神经网络,回声状态网络主要有 2 点不同:1)回声状态网络的隐层规模非常大,需要大约 30~1 000 个神经元。这些大量神经元之间进行稀疏的连接,称为“储备池”。储备池中的大量神经元可以将输入信号映射到高维空间,因此回声状态网络具有非常强的非线性处理能力。2)回声状态网络的训练过程只调整隐层到输出层的连接权值,解决了训练过程中权值之间耦合的问题,使得训练过程大大简化。
设回声状态网络包含 p 个输入单元:
| $ u(n) = {[{u_1}(n),{u_2}(n),\cdots ,{u_p}(n)]^{\rm T}}\text{,} $ |
i 个输出单元:
| $ y(n) = {[{y_1}(n),{y_2}(n),\cdots ,{y_i}(n)]^{\rm T}}\text{,} $ |
|
图 2 回声状态网络与普通递归神经网络对比 Fig. 2 Comparison of Echo state networks and normal recurrent neural networks |
则储备池神经元状态按式(1)进行更新:
| $ x(n + 1) \!=\! f(W_{res}^{in}u(n \!+\! 1) \!+\! {W_{res}}x(n) \!+\! W_{res}^{back}y(n))\text{,} $ | (1) |
其中
回声状态网络的输出方程为:
| $ y(n) = {W^{out}}x(n)\text{。} $ | (2) |
权值
首先,要找到二者的映射关系。假定训练数据 data 的长度为 m,通过滑动窗口来建立一个训练数据矩阵
在大量的实测数据中,仅选取 2 段数据进行仿真预报。第 1 段数据为某船 6 月 14 日第 27 个记录周期的横摇数据,根据实测数据可计算出三一值为 1.63°。
第 2 段数据为某实习训练船在海参崴到元山的航程中的一段纵摇数据,根据实测数据,可以计算出三一值为 0.7 °。
4.2 实测数据预处理 为了避免输入向量中各变量相差过大影响训练效果,支持向量机的训练数据样本要进行归一化处理。设
| $ \bar x = \frac{{{x_i}-{x_{\min }}}}{{{x_{\max }}-{x_{\min }}}}\text{,} $ | (3) |
使训练数据转换到
| $ {x_i} = \left( {{x_{\max }}-{x_{\min }}} \right)\bar x + {x_{\min }}\text{。} $ | (4) |
通过归一化处理,可以使船舶摇荡数据能够在有效数据空间均匀分布开。
4.3 预报效果分析
|
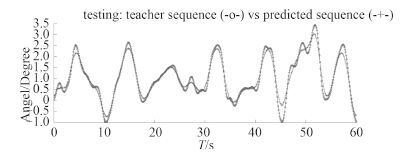
图 3 对某船横摇数据连续预报结果 Fig. 3 Continuous roll forecasting of a target ship |
|
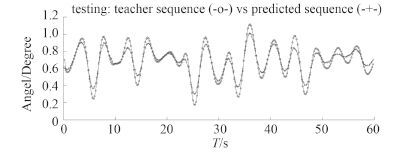
图 4 某训练船纵摇数据连续预报结果 Fig. 4 Continuous pitch forecasting of a training ship |
为了评价模型的预测性能,采用测量误差相对三一值的误差对预测效果进行评估:
| $ SMAPE = \frac{{\left| {{x_{m + i}}-x_{m + i}^ * } \right|}}{{{x_{1/3}}}}\text{。} $ | (5) |
式中:
为便于比较,本实验均对某船的横摇数据和某训练船的纵摇数据均每次向前预报 15 s,连续预报 4 次,即共预报 60 s。误差随预报长度变化如图 5 和图 6 所示。
|
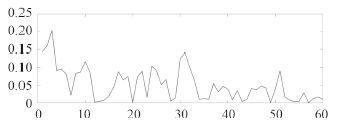
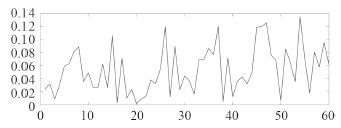
图 5 某船横摇数据预报连续 15 秒时,相对三一横摇值的误差 Fig. 5 The relative error corresponding to significant roll data of a target ship while performing 15 seconds forecasting |
|
图 6 某训练船纵摇数据连续 15 秒时,相对三一纵摇值的误差 Fig. 6 The relative error corresponding to significant pitch data of a training ship while performing 15 seconds forecasting |
结合回声状态网络(ESNs)在非线性处理方面的优势,建立了连续预报算法,该算法运算速度快,能满足实时运算的要求,兼顾了训练误差风险和实时船舶摇荡数据的变化,模型具有需要样本少、泛化能力强的优点,适用于船舶摇荡运动的在线预报。
从图 5 和图 6 可看出,连续预报 60 s 的平均相对误差低于 20%,且多数时间内相对误差低于 15%。可见,对于实船摇荡时历的预报,本文提出的回声状态网络方法的有效预报时长约为 2 个摇荡周期,基本能满足实船极短期预报的需要。
| [1] | 刘孙波, 施平安, 陈聚和. 舰船波浪中运动时域预报方法研究[J]. 广州航海学院学报 , 2014, 22 (2) :21–23. |
| [2] | 彭秀艳, 赵希人, 魏纳新, 等. 大型舰船姿态运动极短期预报的一种AR算法[J]. 船舶工程 , 2001 (5) :5–7. |
| [3] | 彭秀艳, 刘长德. 基于格型递归最小二乘算法的船舶运动极短期预报[J]. 船舶力学 , 2012, 16 (1/2) :44–51. |
| [4] | 王琳. 基于CMAC神经网络的舰船运动预报仿真研究[J]. 数学的实践与认识 , 2014, 44 (23) :160–165. |
| [5] | 刘博, 蔡烽, 石爱国. 舰船摇荡预报中的双变量局域线性多步预报法[J]. 中国航海 , 2012, 35 (2) :33–38. |
| [6] | 陈远明, 叶家玮, 张兮龙. 船舶运动的极短期预报试验[J]. 船海工程 , 2010, 39 (1) :13–15. |
| [7] | 侯建军, 常小勇, 石爱国. 舰船摇荡运动数据采集及混沌特性分析[J]. 船舶工程 , 2011, 33 (6) :25–28. |
| [8] | JAEGER H, HAAS H. Harnessing nonlinearity:predicting chaotic systems and saving energy in wireless communication[J]. Science , 2004, 304 (5667) :78–80. DOI:10.1126/science.1091277 |
| [9] | 郭嘉. 回声状态网络分类方法及其应用研究[D]. 哈尔滨:哈尔滨工业大学, 2011. |
 2016, Vol. 38
2016, Vol. 38
