近年,海军舰船越来越多地走向大洋开展训练与演习,如何能够实时掌握、显示参演兵力的演习进展以及舰船的各种状态成为了海军指挥信息系统发展中一项迫切需要解决的问题[1]。OceanInfo 三维海洋环境信息可视化平台作为一款完全自主研发的三维显示系统开发平台,基于全球构架,提供从全球范围场景到高度精细局部模型的实时可视分析工具,可灵活实现天气模拟、舰船运动实时监控与显示、舰船操纵运动仿真等多种功能,为海空兵力的实时监控提供了一个有效的解决方案。OceanInfo 平台具备强大的功能扩充性,可以通过加装外部控制设备,对舰船的操纵运动进行准确模拟,有效解决舰船操纵训练的保障问题。图 1 所示为基于 OceanInfo 平台的模拟海空演习场景,图 2 所示为舰船操纵运动的模拟训练实地场景。
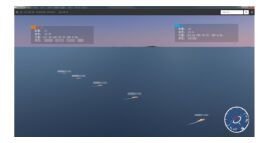
|
图 1 模拟海空演习场景 Fig. 1 Scene of military manoeuvre simulation |

|
图 2 舰船操纵运动模拟 Fig. 2 Ship steering simulation |
本文针对 OceanInfo 平台中的舰船操纵运动模型控制问题展开研究,采用易于工程实现的 PID 控制器,针对其控制参数难以确定的问题,提出一种改进的动态混沌粒子群算法进行控制器的参数整定,有效实现了平台中舰船操纵运动的混沌控制和高精度航向保持。
1 OceanInfo 平台舰船操纵运动模型 为了实现舰船操纵运动特别是航向保持运动的准确模拟,平台采用整体型的船舶数学模型,构建了多型舰船的响应型非线性船舶运动模型[2]。同时,为反映波浪对舰船操纵的影响,引入了波浪作用,根据 Bech 非线性模型[3],在平台的舰船操纵运动控制中,将浪力等效舵角与实际舵角 δ 一起进入模型,并对舰船转首角速度作比例反馈控制[4-6],令舵角 δ = Kp(r0-r),取 r0 = B·sinωt,模型的状态变量为舰船转首角速度 r 及转首角加速度
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2},}\\ {{{\dot x}_2} =-(a + e \cdot {K_p}){x_2}-(b + d \cdot {K_p}){x_1}-cx_1^3}+\\ {\;\;\;\;\; d \cdot {K_p}B\sin (\omega t) + e \cdot {K_p}B\omega \cos (\omega t) \text{。}} \end{array}} \right. $ | (1) |
式中各参数计算见参考文献[5]。
2 航向保持中的混沌问题舰船操纵运动模拟中的航向保持是平台的一项重要功能,针对高精度航向保持的要求,考察式(1)模型,发现,在波浪作用下,当船的阻尼项系数 a 和刚度项系数 b 相差不是很大时,通过反馈增量的补偿,阻尼项系数和刚度项系数是同一数量级,在给定值 r0 较小的情况下,系统将进入非线性混沌状态,即舰船在航向保持过程中会出现混沌现象[5, 7]。
以某型舰船为例,计算得到模型中的各参数,取 kp = 4.5,
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2},}\\ {{{\dot x}_2} =-0.320 \,8{x_2} + 0.2715{x_1}-4.394 \,5x_1^3}+\\ {\;\;\;\;\; 0.103 \,68\cos (0.8t) + 0.078 \,8\sin (0.8t) \text{。}} \end{array}} \right. $ | (2) |
取初值
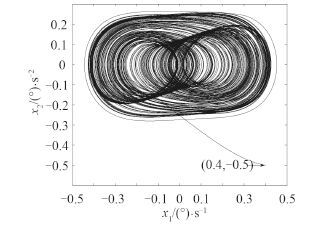
|
图 3 系统相位图 Fig. 3 Figure of system phase |
为了保证平台功能的实现,必须对航向保持中的混沌状态进行控制,使得舰船能够稳定在指定的航向上。基于 PID 控制的特点及其广泛应用[8],本文采用基于混沌系统的改进粒子群优化算法进行 PID 控制器的参数整定,实现了平台中舰船操纵运动的高精度航向保持。
3 PID 参数改进混沌粒子群优化整定 3.1 改进混沌粒子群优化算法根据大量的研究结论[9],惯性权重系数在 PSO 算法中具有重要作用,因此,本文在 PID 控制器的参数整定中首先对 PSO 算法的惯性权重系数进行非线性动态改进,令
| $ {\omega _{(t + 1) }} = {\omega _{\min }} + \frac{{({\omega _{\max }}-{\omega _{\min }})}}{{{e^{(t \times \frac{{{f_{{\rm{t}}\_{\rm{avg}}}}}}{{{f_{\max }}-{f_{\min }}}})}}}} \text{。} $ | (3) |
式中:t 为当前迭的代次数;ft avg 为 t 次迭代后种群粒子适应度值的平均值;fmax,fmin 分别为当前种群的最大和最小适应度值;ω 取值范围为 [ωmin,ωmax]。本文研究和实验表明,在一次搜索中,ω 的变化只取决于当前种群粒子的分布及适应度值情况,避免了算法过早收敛。
同时,为提高优化算法的搜索性能及效率,结合 PID 控制器的参数结构,在 PSO 算法中引入了 Lorenz 混沌序列,通过混沌序列动态地改变种群粒子的位置,进行粒子的再分布,提高算法的搜索效率。
Lorenz 系统是最早得到研究的混沌动力学系统,考察 Lorenz 方程,发现该系统恰好有 3 个状态变量 x,y,z,可对应为种群粒子位置的三维向量(即为 PID 控制器的 3 个参数),同时由于系统具有明显的混沌特征,本文选择将该系统引入优化算法,用于种群粒子在陷入局部最优后获得继续搜索的能力。当优化算法达到设定的条件(即种群粒子连续 k 次适应度值没有改善)时,产生一个三维随机向量初始值
1)初始化。设定混沌迭代步数 M,迭代步长
2)混沌扰动。根据 M 和
3)扰动结果判断。若
针对舰船操纵运动模型,对 PID 控制器的参数进行优化就是要找到恰当的数值,使得受控混沌系统的某个指标最优。PID 控制器参数的改进混沌粒子群优化算法整定流程如下:
1)种群初始化。在可行解空间内初始化种群的规模 N,种群粒子的初始位置、速度,种群中每一粒子为 PID 控制器参数构成的三维向量 x0 = [x01,x02,x03]T,设置最大演化步数 n 等参数,对种群粒子的位置、速度进行范围限制。
2)适应度值计算。根据 OceanInfo 平台采用的舰船操纵运动模型,计算种群粒子的适应值,确定种群的当前局部最优位置 pi 和全局最优位置 pg。选择 ITSE 指标作为适应度函数:
| $ ITSEF:itness{\rm{ = }}\int_0^{ + \infty } {{t^2}{e^2}\left( t \right){\rm{d}}t} \text{。} $ | (4) |
3)种群粒子更新。依据本文的改进 PSO 算法对种群粒子位置、速度、种群局部最优位置 pi 和全局最优位置 pg 进行更新,判断粒子是否陷入局部最优,采用如下的标准:
| $ {\Delta _{fi}} = \frac{{|{f_i}-{f_{pbesti}}|}}{{{f_{pbesti}}}},(i = 1,2,\cdots ,n) \text{。} $ | (5) |
式中,fi 为粒子当前适应度值;
4)终止条件判断。若优化算法满足所设定的终止条件(达到最大演化步数或受控混沌系统输出达到设计指标),停止种群演化,输出全局最优位置;反之,返回步骤2。
4 舰船混沌运动的 PID 控制研究 4.1 PID 控制器设计针对 OceanInfo 平台中航向保持要求及模型特点,采用 PID 控制器进行控制,目标是消除系统的混沌运动,同时使得舰船运动保持在指定航向上,此时,受控系统可写为:
| $ \left\{ \begin{aligned} \,{{\dot x}_1} = & {x_2},\\ \,{{\dot x}_2} = &-0.3208{x_2} + 0.2715{x_1}-4.3945x_1^3 + \\ & 0.10368\cos (0.8t) + 0.0788\sin (0.8t) + u(t),\\ \!\!\!\! u(t) & = {K_p}e(t) + {K_i}\int {e(t){\rm{d}}t + {K_d}\frac{{{\rm{d}}e(t)}}{{{\rm{d}}t}}} \text{。} \end{aligned} \right. $ | (6) |
式中:
根据式(6)所示受控系统,当控制作用为 0 时(即
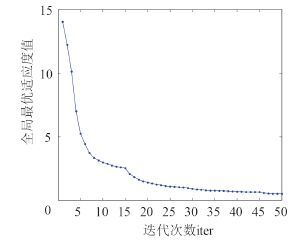
|
图 4 种群适应度值曲线 Fig. 4 Curve of fitness |
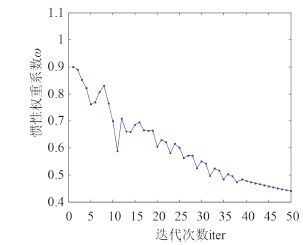
|
图 5 惯性权重系数 ω 曲线 Fig. 5 Curve of inertial weight ω |
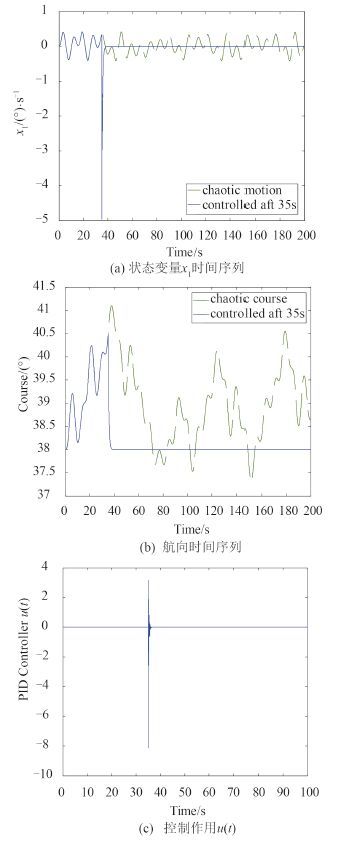
为了验证 PID 控制器优化结果的控制效果,选择在 t = 35 s 时加入 PID 控制作用,目标是控制状态变量
|
图 6 本文改进算法优化的PID控制过程 Fig. 6 Process of PID control optimized by our algorithm |
本文为了实现基于 OceanInfo 平台的模拟舰船操纵运动及航向控制功能,针对受到波浪影响情况下出现的舰船混沌运动控制,采用了 PID 控制器,并对其参数整定提出了一种易于实现的改进动态混沌粒子群优化算法,有效提高了优化算法的搜索性能。实验研究结果表明,本文所提方法在控制器参数整定上具有良好的作用效果,其整定结果控制效果明显,航向保持精度高。
| [1] |
李耀阳, 郭涛, 刘敬明. 浅议虚拟技术在海军指挥信息系统中的应用[J]. 电子测试 , 2015 (5) :141–142.
LI Yao-yang, GUO Tao, LIU Jing-ming. Application of virtual technology in the naval command information system[J]. Electronic Test , 2015 (5) :141–142. |
| [2] | 张显库. 船舶运动简捷鲁棒控制[M]. 北京: 科学出版社, 2012 . |
| [3] | BECH M I. Alternative procedure for carrying out spiral tests[C]. Scandinavian Ship Technical Symposium, Malmo, 1966. |
| [4] |
李芃, 张晓宇, 何晋, 等. 船舶运动控制中的非线性混沌及PID控制方法[J]. 舰船科学技术 , 2002, 24 (5) :36–39.
LI Peng, ZHANG Xiao-yu, HE Jin, et al. The nonlinear chaos in ship movements control and PID controlling chaos[J]. Ship Science and technology , 2002, 24 (5) :36–39. |
| [5] |
苏宁. 混沌学与船舶运动控制[D]. 大连:大连海事大学, 1996.
SU Ning. Chaos and ship steering control[D]. Dalian:Dalian Maritime University, 1996. |
| [6] |
朱璐. 船舶航向保持中的混沌及鲁棒控制[D]. 大连:大连海事大学, 2009.
ZHU Lu. Chaos in course keeping for ships and its robust control[D]. Dalian:Dalian Maritime University, 2009. |
| [7] | HUANG Q, LIU X G, LI T W, et al. On impulsive parametric perturbation control techniques for chaotic ship steering[C]//Proceedings of IEEE Chinese Guidance, Navigation and Control Conference. Yantai:IEEE, 2014:428-433. |
| [8] |
罗文广, 于滢源, 谢广明, 等. 一类切换系统的混沌行为分析及混沌控制研究[J]. 深圳大学学报(理工版) , 2013, 30 (3) :235–241.
LUO Wen-guang, YU Ying-yuan, XIE Guang-ming, et al. Chaotic behavior analysis for a type of switched systems and its chaotic control[J]. Journal of Shenzhen University Science and Engineering , 2013, 30 (3) :235–241. DOI:10.3724/SP.J.1249.2013.03235 |
| [9] |
李宁, 刘飞, 孙德宝. 基于带变异算子粒子群优化算法的约束布局优化研究[J]. 计算机学报 , 2004, 27 (7) :897–903.
LI Ning, LIU Fei, SUN De-bao. A study on the particle swarm optimization with mutation operator constrained layout optimization[J]. Chinese Journal of Computers , 2004, 27 (7) :897–903. |
 2016, Vol. 38
2016, Vol. 38
