2. 海洋石油工程股份有限公司, 天津 300461
2. Offshore Oil Engineering Co., Ltd., Tianjin 300461, China
水路运输是物流运输的重要组成部分。近年来,随着航运业的日益繁荣,港口通航密度的增加,拖航业务也逐渐进入繁忙阶段,人们对于拖航业务的重视也大大提高。一直以来,拖航作业操纵系统主要是靠船长和引航员的经验来操船,而没有一套非常全面有效的控制方式,这种操纵方式很难较精确地设定和控制拖航系统的航线,同时也可能增加了拖航航行的危险系数。因此,研究拖航作业系统的操纵性,对于保障拖航业务的安全,减少海上拖航运输事故,保证拖航作业顺利进行以及防止海洋污染有重要意义。
从 20 世纪 50 年代开始,就有国外学者对拖航作业系统的操纵性能及航向稳定性展开研究。拖航系统研究随着船舶操纵性研究的发展也在不断进步。1985 年 Bernitsas and Kekridis [1]就开始建立三自由度模型研究一系列弹性拖缆拖带系统的稳定性。1998 年 Leite等[2]研究的三自由度模型,仅需要知道船舶的主要船型系数就可以建立。2007 年 Yasukawa 等[3]对拖轮拖航系统的回转运动进行仿真,讨论了拖缆长度的影响。2013 年 Fitriadhy 和 Yasukawa [4]研究了在定常风下的拖航系统线性和非线性模型的航向稳定性。2014 年 Marco Sinibaldi 和 Gabriele Bulian [5]研究了风影响下的非线性四自由度的拖航仿真。
国内关于拖航系统的研究较少,梁康乐等[6]初步建立考虑浅水因素影响的三自由度模型,孙洪波等[7]研究了静水下的四自由度仿真。
拖航系统的航向稳定性影响拖航作业的效率、经济性和安全性,航向稳定性是拖航作业的首要前提。在现有的理论和研究基础上,建立由拖轮、拖缆、被拖船组成的拖航系统在风、浪、流影响下的六自由度操纵数学模型,然后编制仿真程序,通过数值计算对拖航作业系统操纵运动进行实时模拟仿真。模拟拖航系统的直航和回转作业,调整拖航航速、拖缆长度,得到不同工况下的运动数据。分析在静水中拖航速度、拖缆长度对拖航直航、回转及航向稳定性的影响,改变环境条件,分析风、浪、流对拖航作业系统运动的影响,仿真模拟的结果对实际拖航作业有一定参考作用。
1 拖航系统六自由度运动数学模型 1.1 基本假设本文研究的拖航系统由拖船和无自航能力的船舶组成,拖航形式为一列式拖带,在建立运动模型时,假定:1)拖船和被拖船之间的距离足够大,忽略它们之间的水动力干扰,运动仅由拖缆耦合,满足悬链线模型;2)被拖船无自航能力,不考虑其螺旋桨和舵作用力;3)只考虑定常风、规则波、均匀定常流的影响,风与波浪、水流互不干扰;4)拖航运动中,拖缆对船舶升沉和纵摇的影响只与拖缆重力有关。
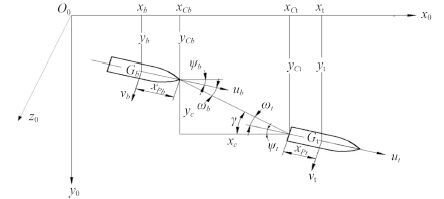
1.2 坐标系和操纵运动模型图 1 为拖航系统坐标系,根据 MMG 操纵性方程,可以得到拖航系统六自由度操纵运动数学模型。
|
图 1 坐标系 Fig. 1 Coordinate system |
拖船操纵运动方程为:
| $ \left\{ \begin{aligned} & ({m_{\rm{t}}} \!+\! {\lambda _{11}}_{\rm{t}}){{\dot u}_{\rm{t}}} \!-\! ({m_{\rm{t}}} \!+\! {\lambda _{22}}_{\rm{t}}){r_{\rm{t}}}{v_{\rm{t}}} \!=\! {X_H}_{\rm{t}} \!+\! {X_P}_{\rm{t}} \!+\! {X_R}_{\rm{t}} \!+\! {X_W}_{\rm{t}} \!+\! \\[2pt] & \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,{X_F}_{\rm{t}} \!+\! {X_{Ct}} \!+\! {X_{Tt}}\text{,}\\[2pt] & ({m_{\rm{t}}} + {\lambda _{22}}_{\rm{t}}){{\dot v}_{\rm{t}}} \!+\! ({m_{\rm{t}}} \!+\! {\lambda _{11}}_{\rm{t}}){r_{\rm{t}}}{u_{\rm{t}}} \!=\! {Y_H}_{\rm{t}} \!+\! {Y_P}_{\rm{t}} \!+\! {Y_R}_{\rm{t}} \!+\! {Y_W}_{\rm{t}} \!+\! \\[2pt] & \qquad\qquad\qquad\qquad\quad\quad\quad\,\,\,\,\,{Y_F}_{\rm{t}} \!+\! {Y_{Ct}} \!+\! {Y_{Tt}}\text{,}\\[2pt] & ({m_t} + {\lambda _{33}}_{\rm{t}}){{\dot \omega }_t} \!+\! {m_{\rm{t}}}({p_t}{v_t} \!-\! {q_t}{u_t}) \!=\! {Z_H}_{\rm{t}} \!+\! {Z_W}_{\rm{t}} \!+\! \\[2pt] & \qquad\qquad\qquad\qquad\qquad\quad\quad\,{Z_F}_{\rm{t}} \!+\! {Z_{Tt}}\text{,}\\[2pt] & ({I_{xt}} \!+\! {\lambda _{44}}_{\rm{t}}){{\dot p}_t} \!+\! ({I_{zt}} \!-\! {I_{yt}}){q_t}{r_t} \!=\! {L_{Ht}} \!+\! {L_{Rt}} + {L_{Wt}} \!+\! \\[2pt] & \qquad\qquad\qquad\qquad\qquad\quad {L_{Ft}} \!+\! {L_{Tt}}\text{,}\\[2pt] & ({I_{yt}} \!+\! {\lambda _{55}}_{\rm{t}}){{\dot q}_t} \!+\! ({I_{xt}} \!-\! {I_{zt}}){r_t}{p_t} \!=\! {M_{Ht}} \!+\! {M_{Pt}} \!+\! {M_{Rt}} \!+\! \\[2pt] & \qquad\qquad\qquad\qquad\qquad\quad {M_{Wt}} \!+\! {M_{Ft}} \!+\! {M_{Tt}}\text{,}\\[2pt] & ({I_z}_{\rm{t}} \!+\! {\lambda _{66}}_{\rm{t}}){{\dot r}_{\rm{t}}} \!=\! {N_H}_{\rm{t}} \!+\! {N_P}_{\rm{t}} \!+\! {N_R}_{\rm{t}} \!+\! {N_W}_{\rm{t}} \!+\! \\[2pt] & \qquad\qquad\quad\,\,{N_F}_{\rm{t}} \!+\! {N_{Ct}} \!+\! {N_{Tt}}\text{,} \end{aligned} \right. $ | (1) |
被拖船操纵运动方程:
| $ \left\{ \begin{aligned} & ({m_b} \!+\! {\lambda _{11}}_b){{\dot u}_b}-({m_b} \!+\! {\lambda _{22b}}){r_b}{v_b} \!=\! {X_H}_b \!+\! {X_W}_b \!+\! {X_F}_b \!+\! \\ & \qquad\qquad\qquad\qquad\qquad\qquad\quad {X_{Cb}} + {X_{Tb}}\text{,}\\ & ({m_b} \!+\! {\lambda _{22}}_b){{\dot v}_b} \!+\! ({m_b} \!+\! {\lambda _{11}}_b){r_b}{u_b} \!=\! {Y_H}_b \!+\! {Y_W}_b \!+\! {Y_F}_b \!+\! \\ & \qquad\qquad\qquad\qquad\qquad\quad\quad\,\,\,{Y_{Cb}} + {Y_{Tb}}\text{,}\\ & ({m_b} \!+\! {\lambda _{33}}_b){{\dot \omega }_b} \!+\! {m_b}({p_b}{v_b} \!-\! {q_b}{u_b}) \!=\! {Z_H}_b \!+\! {Z_{Wb}} \!+\! \\ & \qquad\qquad\qquad\qquad\qquad\qquad\quad {Z_F}_b + {Z_{Tb}}\text{,}\\ & ({I_{xb}} \!+\! {\lambda _{44}}_b){{\dot p}_b} \!+\! ({I_{zb}} \!-\! {I_{yb}}){q_b}{r_b} \!=\! {L_{Hb}} \!+\! {L_{Wb}} \!+\! \\ & \qquad\qquad\qquad\qquad\qquad\quad\quad {L_{Fb}} + {L_{Tb}}\text{,}\\ & ({I_{yb}} \!+\! {\lambda _{55}}_b){{\dot q}_b} \!+\! ({I_{xb}} \!-\! {I_{zb}}){r_b}{p_b} \!=\! {M_{Hb}} \!+\! {M_{Wb}} \!+\! \\ & \qquad\qquad\qquad\qquad\qquad\quad\quad {M_{Fb}} + {M_{Tb}}\text{,}\\ & ({I_z}_b \!+\! {\lambda _{66}}_b){{\dot r}_b} \!+\! ({I_{yb}} \!-\! {I_{xb}}){p_b}{q_b} \!=\! {N_H}_b \!+\! {N_W}_b \!+\! {N_F}_b \!+\! \\ & \qquad\qquad\qquad\qquad\qquad\quad\quad {N_{Cb}} + {N_{Tb}}\text{。} \end{aligned} \right. $ | (2) |
式中:XTt,YTt,ZTt,LTt,MTt,NTt 为拖缆作用在拖轮上的拖缆力(矩);XTb,YTb,ZTb,LTb,MTb,NTb 为拖缆作用在被拖轮上的拖缆力(矩);下标 t 和 b 分别为拖船和被拖船;下标 H、P、R、W、F、C、T 为船体水动力、螺旋桨力、舵力、波浪力、风力、水流力。各参数表示物理意义参见文献[8]。
1.3 拖航系统水动力计算模型 1.3.1 船体水动力作用于船体上的船体惯性类水动力以船体附加质量和船体惯性矩的形式进行处理。船体粘性类水动力模型如下:
| $ \left\{ \begin{aligned} {X_H} = & X(u) + {X_{vv}}{v^2} + {X_{vr}}vr + {X_{rr}}{r^2}\text{,}\\ {Y_H} = & {Y_v}v + {Y_r}r + {Y_{v\left| v \right|}}v\left| v \right| + {Y_{v\left| r \right|}}v\left| r \right| + \\ & {Y_{r\left| r \right|}}r\left| r \right| + {Y_{vvr}}{v^2}r + {Y_{vrr}}v{r^2}\text{,}\\ {N_H} = & {N_v}v + {N_r}r + {N_{v\left| v \right|}}\left| v \right|v + {N_{r\left| r \right|}}r\left| r \right| + \\ & {N_{vvr}}{v^2}r + {N_{vrr}}v{r^2}\text{。} \end{aligned} \right. $ | (3) |
式中:X(u)为船舶直航时所受到的船体阻力;Xvv,Xvr,Xrr 为纵向非线性水动力导数;Yv,Yr,Yv|v|,Yv|r|,Yr|r|,Yvvr,Yvrr 分别为船舶横向线性和非线性水动力导数;Nv,Nr,Nv|v|,Nr|r|,Nvvr,Nvrr 分别为转首线性和非线性水动力导数。
船体横摇水动力矩:
| $ ({I_x} + {\lambda _{44}})\ddot \varphi + 2{L_{\dot \varphi }}\dot \varphi + \Delta \cdot GZ(\varphi ) + {Y_H} \cdot {z_H} = {L_H}\text{,} $ | (4) |
船体垂荡水动力和纵摇水动力矩:
| $ \left\{ \begin{array}{l} (m + {\lambda _{33}})\ddot z + {Z_{\dot z}}\dot z + {Z_z}z + {Z_{\ddot \theta }}\ddot \theta + {Z_{\dot \theta }}\dot \theta + {Z_\theta }\theta = {Z_\Sigma }\text{,}\\ ({I_y} \!+\! {\lambda _{55}})\ddot \theta \!+\! {M_{\dot \theta }}\dot \theta \!+\! {M_\theta }\theta \!+\! {M_{\ddot z}}\ddot z \!+\! {M_{\dot z}}\dot z + {M_z}z = {M_\Sigma }\text{。} \end{array} \right. $ | (5) |
式中各水动力导数可由经验公式求得,公式中各参数表示意义物理参见文献[8]。
1.3.2 拖船桨、舵水动力拖船一般多为双桨双舵船,螺旋桨推力可用下式进行计算:
| $ \left\{ \begin{array}{l} {X_P} = (1-t)({T_L} + {T_R})\text{,}\\ {M_P} = {X_P} \cdot {z_P}\text{,}\\ {N_P} = b(1-t)({T_L}-{T_R})/2\text{。} \end{array} \right. $ | (6) |
式中:TL 为左边螺旋桨的推力;TR 为右边螺旋桨的推力;b 为桨之间的横向距离。舵作用力的计算和螺旋桨力的计算采用相似的处理方法,拖船的舵力公式为:
| $ \left\{ \begin{array}{l} {X_R} =-\left( {1-{t_R}} \right){F_N}\sin \delta\text{,} \\ {Y_R} = \left( {1 + {\alpha _H}} \right){F_N}\cos \delta\text{,} \\ {L_R} =-{Y_R}\times{z_R}\text{,}\\ {M_R} = {X_R}\times{z_R}\text{,}\\ {N_R} = {x_R}(1 + {\alpha _H}){F_N}\cos \delta \text{。} \end{array} \right. $ | (7) |
式中:FN 为舵的法向力;δ 为船舶实际舵角(左舵为正);tR 为舵力减额系数,本文采用近似估算公式进行估算;xR 为舵中心的纵向坐标;αH 为船体横向力受到操舵影响的系数;zR 为 FN 作用点在运动坐标系下的纵向坐标。
1.4 环境因素模型 1.4.1 风本文仅考虑定常风对于拖航操纵性的影响,计算模型为:
| $ \left\{ \begin{array}{l} {X_W} =-{R_a}\cos {\alpha _a}\text{,}\\ {Y_W} = {R_a}\sin {\alpha _a}\text{,}\\ {L_W} = {Y_W}{z_s}\text{,}\\ {M_W} = {X_W}{z_f}\text{,}\\ {N_W} = {Y_W}({l_G}-a)\text{。} \end{array} \right. $ | (8) |
式中:Ra 为风压合力;αa 为风压合力角;zs 为水线上侧投影面积中心的垂向坐标绝对值;zf 为水线上正投影面积中心的垂向坐标绝对值;lG 为船舶重心到船首的纵向距离;a 为风压合力作用点位置到船舶首部的距离。
1.4.2 浪计算波浪力时,假设船体所受到的波浪力与力矩只由流体压力产生,波浪不受船舶运动影响,且为规则波。波浪力计算公式为:
| $ \left\{ \begin{aligned} {X_{F2}} = & 0.5\rho gL\xi _W^2{C_{XW}}\cos \chi\text{,} \\ {Y_{F2}} = & 0.5\rho gL\xi _W^2{C_{YW}}\sin \chi \text{,}\\ {N_{F2}} = & 0.5\rho g{L^2}\xi _W^2{C_{NW}}\sin \chi \text{。} \end{aligned} \right. $ | (9) |
式中:ξW 为平均波浪幅值;CXW,CYW,CNW 为波浪漂移力系数。
1.4.3 流在计算水流作用力时,仅考虑均匀定常流的影响:
| $ \left\{ \begin{aligned} {X_{\rm{C}}} = & rV_C^{}\sin (\psi-{\psi _{\rm{C}}})({\lambda _{11}}-{\lambda _{22}})\text{,}\\ {Y_{\rm{C}}} = & rV_C^{}\cos (\psi-{\psi _{\rm{C}}})({\lambda _{22}}-{\lambda _{11}})\text{,}\\ {N_{\rm{C}}} = & 0\text{。} \end{aligned} \right. $ | (10) |
采用悬链线模型来计算拖缆拉力,加入拖缆弹性影响:
| $ \left\{ \begin{aligned} & H = \frac{{{T_0}(\sec {\theta _0}-1) }}{w}\text{,}\\ & \tan \theta = \frac{{{L_c}w}}{{2{T_0}}}\text{,}\\ & {l_c} = \frac{{2{T_0}}}{w}{\sin\text{h} ^{-1}}(\tan {\theta _0}) + \frac{{{T_0}{L_c}}}{{EA}}\text{,}\\ & {T_V} = \frac{1}{2}w{L_c}\text{。} \end{aligned} \right. $ | (11) |
式中:H 为拖缆的悬垂值;T0 为拖带点处水平方向的拖缆张力合力;TV为拖带点处垂直方向的拖缆力;w 为拖缆单位长度重量;θ0 为拖缆与水平面之间的夹角;Lc 为拖缆长度;lc 为位于两船拖带点之间的拖缆水平距离;E 为拖缆弹性模量;A 为拖缆横剖面积。实际拖航过程中,由于拖缆存在一定悬垂,拖缆入水阻力不容忽视,拖缆入水阻力计算公式:
| $ {R_{\rm{t}}} = 1.224\frac{S}{{1 \; 000}}\frac{d}{{10}}{V^2}[1 + \frac{{1.122}}{{1 \; 000T}}\frac{d}{{10}}{(\frac{S}{{1 \; 000}})^2}]\text{。} $ | (12) |
式中:Rt 为拖缆水平阻力;d 为拖缆的直径;S 为拖缆浸入水中两端间距。
在建立拖航系统数学模型时采用 MMG 方程的思想,分别建立拖船、拖缆、被拖船的模型。这种建模方式简单直观,便于为后续进行多船拖带的研究。
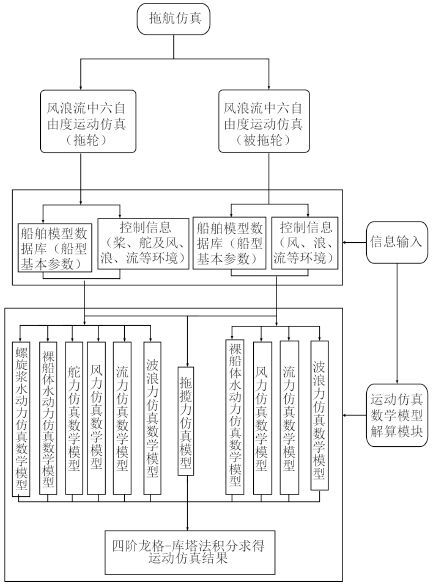
2 拖航系统仿真计算 2.1 仿真程序以拖轮和驳船通过拖缆进行拖带的拖航作业系统为主要研究对象进行操纵运动仿真计算,在拖轮和被拖轮的六自由度操纵性数学模型基础上,结合拖缆和不同环境因素的干扰力数学模型,建立拖航作业系统的数学模型,采用 4 阶显式龙格库塔法编制计算程序求解操纵性方程,设置相关参数、初始变量和时间步长,对拖航作业系统操纵运动进行实时模拟仿真计算。拖航作业系统操纵运动仿真流程如图 2 所示。
|
图 2 仿真流程 Fig. 2 Flow-process diagram |
为验证六自由度操纵仿真程序的稳定性与准确性,以德惠拖轮和“海洋石油 229”导管架驳船作为被拖船为例进行运动仿真,对拖航作业系统操纵运动进行实时模拟,船舶主尺度、拖船螺旋桨桨、舵尺度、拖缆参数如表 1 所示。
|
|
表 1 船舶主尺度 Tab.1 Dimensions of ships |
实际拖航作业中拖缆最小安全长度由海上拖航技术要求中计算公式来求得,拖缆长度具体对于拖航安全性的影响并没有详细叙述。在仿真实例中对于拖缆长度对于拖航性能影响进行研究,在拖航系统在静水中做直航运动时,按照拖缆长度的选取不同,将运动工况分为 4 种,分别计算不同直航工况下的拖航运动,不同工况运动参数设置如表 2 所示。
|
|
表 2 拖缆长度 Tab.2 Length of rope |
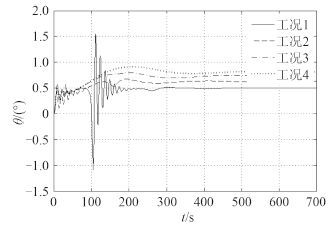
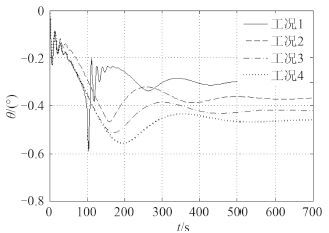
由图 3 和图 4 可知,在相同初始条件下,增加拖缆长度会使拖轮和驳船的纵摇角度增大,每增加 100 m 拖缆长度,拖轮和驳船的纵摇角会平均增加 0.1°,但在拖缆长度过短时,拖轮和驳船在运动过程初期纵摇幅度和频率剧烈变化,对拖航运动极为不利,拖缆长度适当时,纵摇波动和幅度减小且会在一段时间后到达平稳状态。静水中拖航系统拖缆长度增加,首向角波动幅度减小,拖航系统航向稳定性增加[6]。
|
图 3 直航时拖轮纵摇角对比曲线 Fig. 3 Typical graph of tug’s pitch angles |
|
图 4 直航时驳船纵摇角对比曲线 Fig. 4 Typical graph of barge’s pitch angles |
但增加拖缆长度会相应增加整个拖航系统的回转半径,使得整个系统的回转性能变差,拖缆长度每增加 50 m,拖航回转半径会平均增大 100 m 左右,在实际操纵过程中为了保证回转性能就需要辅助拖船协助驳船转向,而且拖缆长度增加在拖带过程中浸水阻力和拖缆悬垂度增加。
通过仿真实例计算总结的规律:在拖航运动中,拖缆长度设置不应过短,拖缆长度过短会增加整个系统的摇荡幅度和频率,使拖航稳定性变差,拖缆长度也不应设置过长,拖缆长度增加,整个拖航系统的纵摇角度加大,回转半径加大,浸水阻力增大,在实际作业中考虑作业环境和作业要求选取适当拖缆长度。
3.2 拖航速度的影响为了研究拖航速度对于拖航作业的影响,考虑拖缆长度为 300 m 时,提高主机转速,使拖航稳定航速提升至 3 m/s,其余参数与拖缆长度工况 3 设置相同,将拖航运行时的拖缆力曲线、速度曲线和姿态角曲线分别与工况 3 进行对比,对比曲线如图 5~图 8 所示。
|
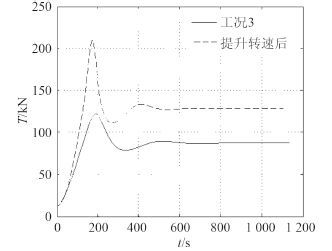
图 5 速度变化前后拖缆力对比曲线 Fig. 5 Typical graph of towing force in different speeds |
|
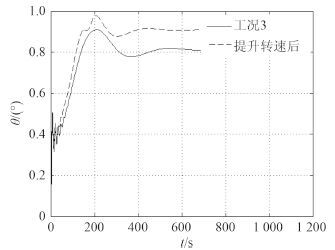
图 6 速度变化前后拖轮纵摇对比曲线 Fig. 6 Typical graph of tug’s pitch angle in different speeds |
|
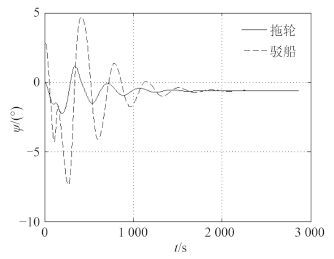
图 7 工况 3 首向角的变化曲线 Fig. 7 Heading angles of condition 3 |
|
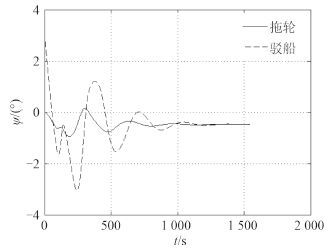
图 8 加速后首向角的变化曲线 Fig. 8 Heading angles of condition 3(speed up) |
由图 5 可知,拖航航速增加,拖缆力增大,对拖缆强度要求提高。由图 6 可知,拖航航速提高,拖轮纵摇角有一定幅度加大,对比图 7 和图 8 可知,拖航航速增加,拖航首向角的变化幅度减小,而且首向角到达稳定时间减少,拖航直线稳定性提高。由图 7 和图 8 可知,拖轮和驳船的首向角的变化产生一定的波动,但最终会处于稳定状态说明该拖航系统具有直线稳定性。
通过仿真实例总结的规律:拖航速度增加,拖航系统的首向角波动幅度减小,拖航航向稳定性增加,但随着拖航航速增加,拖航系统纵摇角和拖缆力波动幅度增加,在对于拖航稳定性要求较高且被拖船惯性较大的作业过程拖航航速不宜过大。
3.3 风、浪、流的共同作用下拖航运动拖航系统在海上航行时,风、浪、流等环境因素一般不是单独出现的,可能同时受多种因素影响,使得船舶拖航运动更加复杂多样。考虑风、浪、流的同时作用,风速 10 m/s,2 级海况下,流速 0.1 m/s,将风向、浪向、流向均设为 0°,拖航系统操 35° 舵角时回转运动轨迹、姿态角及拖缆拉力变化曲线分别如图 9~图 10 所示。
|
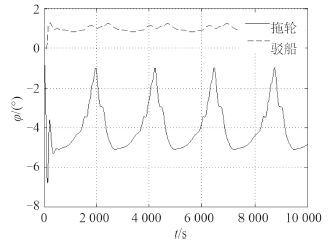
图 9 风浪流作用下横摇角曲线 Fig. 9 Typical graph of roll angles |
|
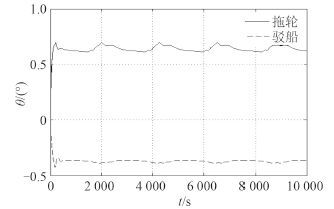
图 10 风浪流作用下纵摇角曲线 Fig. 10 Typical graph of pitch angles |
由图 9~图 10 可知:整个拖航系统操 35° 舵角回转时,受到风、浪、流的影响,拖航系统产生偏移,在环境作用下,被拖船横摇角的变化幅度在-1° ~-5° 周期性变化,拖船纵摇角变化较小约为 0.7°,被拖船纵摇角约为-0.4°,拖缆力变化也较为稳定,满足作业仿真的要求,在后续的视景模拟中可以实时输出拖航信息,顺利完成视景仿真作业。
4 结语基于 MMG 方程思想建立船舶六自由度运动模型,结合考虑拖缆弹性影响的悬链线模型,建立拖航作业系统的六自由度操纵性运动模型,对拖航操纵运动进行实时仿真,验证仿真系统具有直线稳定性,结合仿真实例得出拖航作业拖缆长度不应过长或过短,应结合作业要求对于拖缆长度的影响进行最优化选择,拖航速度可以提高航向稳定性但也会增加系统的摇荡运动,验证拖航系统仿真模型在风、浪、流共同作用影响下的操纵运动实时解算,为实现视景仿真模拟打下基础,对拖航安全作业模拟有指导作用,对实际拖航作业有一定参考价值。
| [1] | BERNITSAS, M. M., KEKRIDIS, N .S. Simulation and Stability of Ship Towing[J]. Int. Shipbuild. Prog , 1985, 32 (369) :112–123. |
| [2] | LEITE, A J P, ARANHA, J A P, UMEDA, C ., et al. Current forces in tankers and bifurcation of equilibrium of turret systems:hydrodynamic model and experiments[J]. Appl.OceanRes , 1998, 20 :145–156. DOI:10.1016/S0141-1187(98)00002-9 |
| [3] | YASUKAWA, H, NAKMURA, N, HIRATA, N, et al. Maneuvering simulations of tow and towed ships in still water[C]//.In:Proceedings of the 1st International Conference on Towing and Salvage of Disabled Tankers (TSDT2007), Glasgow, UK. 200722-23 March. pp. 73-82. |
| [4] | FITRIADHY A, YASUKAWA H, KOH K K. Course stability of a ship towing system in wind[J]. Ocean Engineering , 2013, 64 :135–145. DOI:10.1016/j.oceaneng.2013.02.001 |
| [5] | MARCO S, GABRIELE B. Towing simulation in wind through a nonlinear 4-DOF model:Bifurcation analysis and occurrence of fishtailing[J]. Ocean Engineering , 2014, 88 :366–392. DOI:10.1016/j.oceaneng.2014.06.007 |
| [6] | LIANG K, DENG De-heng, HUANG Guo-liang. A study of towing system maneuvering motion dimulation[J]. Navigation of China , 2007 (2) :10–29. |
| [7] | SUN Hong-bo, WENG Yue-zong. 4-DOF modeling and simulation of marine towing system[J]. Navigation of China , 2012 (2) :39–44. |
| [8] | YAO jing-zheng, HAN duan-feng, ZHAO peng-ju. Research on the simulation of ship towing system[J]. Ship Building of China , 2011, 52 (3) :75–82. |
| [9] | FITRIADHY, A, YASUKAWA H. Course stability of a ship towing system[J]. Ship Technol. Res , 2011, 58 :4–24. DOI:10.1179/str.2011.58.1.001 |
| [10] | YASUKAWA, H, HIRONO, T, NAKAYAMA, Y, et al. Course Stability and Yaw Motion of a Ship in Steady Wind[J]. Marine Science and Technology , 2012, 3 :291–304. |
 2016, Vol. 38
2016, Vol. 38
