2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
Naval ship concept design is on the top of overall design process, via the creation and evaluation of mounts of projects, the optimal project baseline can be obtained[1]. Development of naval ship synthesis model[2] provides the quality platform for ship integrated design. As the core, synthesis model can combine appropriate optimization algorithm to generate mounts of projects from predetermined design space, then combining evaluation method, the optimal design baseline can be quickly formed for further detailed design.
In the mechanism of integrated design based on naval ship synthesis model, this paper introduces Simulated Annealing algorithm (SA), which can effectively avoid local optimum, to research the quick generation of naval ship projects based on single target SA and multiple target SA. Via the reasonable process and internal parameters control, the applicability conclusion of each algorithm is obtained. Because of both quantitative and qualitative indexes existing in a naval ship project, Vague set fuzzy evaluation method is introduced, and intelligent evaluation model, which can effectively integrate all types of indexes, is established, then the advancement and rationality is proved via the comparative analysis. Method researched in this paper can be a great orientation of naval ship project design, and can also be used in other parts of naval ship development.
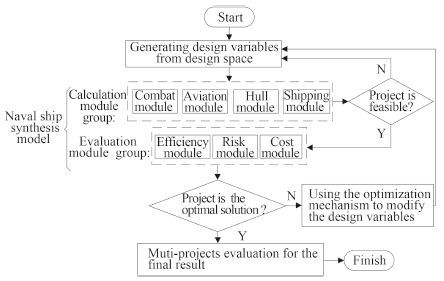
1 Introduction and application mode of naval ship synthesis modelNaval ship synthesis model is used as the key progress in stage of naval ship concept design and projects evaluation, which supports the spiral design and evaluation software model[3]. It is composed by the overall performance evaluation module, analysis of the projects feasibility analyzing module, evaluation module (including evaluation of efficiency, risk and cost), that the group of modules has the data coupling relationship. Synthesis model takes the main system projects and design constraints as input, and naval ship projects which are expressed by a series of design variables as output.[1]
Large surface naval ship[4] is taken as example in this paper, and the integrated design mode based on synthesis model is established after combining specific technical characteristics and introducing optimization and evaluation algorithm, which is shown in figure 1.
|
Fig. 1 Naval ship projects integrated design mode based on synthesis model |
The process above contains these key technologies: establishment technology of accurate naval ship synthesis model, quick creation of naval ship projects based on optimization algorithm technology, and multiple projects evaluation technology. Among these technologies, synthesis model establishment need mounts of the empirical data and real ship test accumulation, and abundant synthesis model library has been developed since the development of integrated design mode for more than half a century. Therefore the two key technologies after are concerned here and research will be done from intelligent optimization and evaluation algorithm.
2 Naval ship project creation based on single target SA algorithmSA algorithm has the strong astringency and accurate result that is suitable for optimization problem of complex system. The only problem is long computing time, which can be improved by reasonable controlling internal parameters and process[5]. The research of naval ship project generations based on single target SA algorithm is taken here.
2.1 Determine the optimization targetThe target function is determined as the weighted integration of efficiency (Eff), Life cycle cost (Lcc) and Risk (Risk). Because Eff is type of “the more the better” index, while Lcc and Risk are type of “the less the better” indexes, the target function of single target optimization is established as formula (1) .
| $ \begin{aligned} \min f(x) = & 1 \, 000 \times [{\omega _1}(1-\displaystyle\frac{{Eff-0.45}}{{1.0-0.45}}) + \\ & \displaystyle{\omega _2}Risk + {\omega _3}\frac{{Lcc-40}}{{120-40}}]\text{。} \end{aligned} $ | (1) |
Among which, x contains all the design variables,
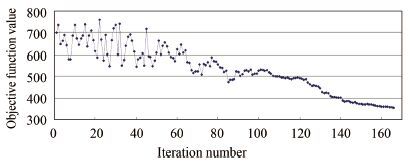
Via choosing the appropriate internal operation parameters of SA, the final optimal result is obtained by 167 times of iterative calculation. The changing curve of target function along with the iterative process is shown in figure 2.
|
Fig. 2 Target function value changing curve |
Fig 2 shows target function value of the initial iteration stage (0 to 60 times) has large amplitude fluctuations, then function value begins steady after about 150 times, so the approximate optimal solution has been reached. Because of the acceptance probability of non optimal solution changing all the time, the deviation between approximate optimal result and global optimal result can be minimization.
3 Naval ship project generations based on multiple targets SA algorithm 3.1 Significance of multiple targets optimization algorithmThe method above in chapter 2 exist the problem: single target optimization function via the simple weighting method makes final result greatly depend on weights makers’ subjective experience. At the same time, the optimization process is divorced from each optimal target, so it make each target has a certain level of sacrifice for the overall optimum. Figure 3 shows the changing of each target when the single optimization process is taken, therefore the final optimal result of each target is not the most optimal result of their own.

|
Fig. 3 Each part target change during the iteration process |
Therefore the multiple targets optimization is introduced, which can generate a series of optimal result according to requirement of each target, and designer can choose the appropriate project from them via the following evaluation.
3.2 Multiple optimization processThe target of multiple optimization problem is the most efficiency, the least risk and cost. SA multiple optimization algorithm[6] also needs to choose the appropriate internal parameters, which can be chosen as the single target algorithm above because of the same design variables perturbation theory.
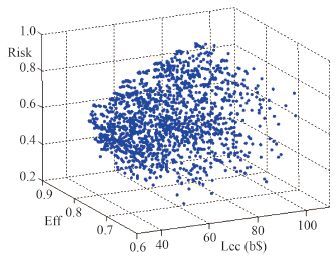
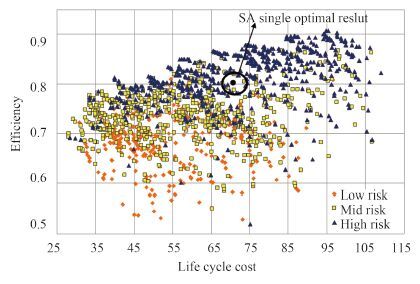
Via 62 times of global iterative calculation, Pareto frontier is formed after searching 1 500 projects. Figure 4 shows the Eff, Risk and Lcc of these 1 500 projects together. For the more intuitive of the results, each project has the classification of risk grade, and there are 3 grades in this paper: low risk (Risk<0.3) , middle risk (0.3<Risk<0.6) and high risk (Risk>0.6) . Eff and Risk two dimensions points figure is shown in figure 5, which shows the overall trend is: high efficiency leads to high cost and high risk, and when efficiency is higher than a certain value (0.8 for example), fewer efficiency enhance will significantly bring the cost growth.
|
Fig. 4 Three dimensions points figure of 1 500 projects |
The optimal project which is obtained in chapter 3 via single target optimization is inserted to figure 5, which isn’t arrived the Pareto frontier, proving the fact that single optimization algorithm is aiming at the global optimal, not the individual optimal, therefore multiple optimization algorithm has the more feasibility for naval ship integrated design process.
|
Fig. 5 Two dimensions points figure of 1 500 projects |
Pareto frontier generated above is on behalf of the optimal projects group concerning about both efficiency and cost. A number of projects can be chosen among them for the designer to determine final project via the high applicability evaluation algorithm. Thus 5 typical projects are chosen here from figure 5 for the following evaluation.
The 5 projects chosen here are formed by both qualitative and quantitative index, though in the design process, some indexes are expressed as quantitative indexes such as combat ability and risk, that they’re usually regarded as fuzzy qualitative indexes. For the rational evaluation process, it’s necessary to do the fuzzy processing of certain indexes. Vague set evaluation method is chosen here[7, 8], which can effectively integrate all types of indexes. The indexes of each project are turned to Vague value according to Vague language variable processing rules[9], which are shown in table 1.
|
|
Tab.1 Vague value of each index |
There are two types of Vague set ordering function, as in formula (2) :
| $ \left\{ {\begin{array}{*{20}{c}} {S(E({A_i})) = {t_{{A_i}}}-{f_{{A_i}}}\text{,}\begin{array}{*{20}{c}} {} & {} \end{array}(a)}\text{。}\\ {H(E({A_i})) = {t_{{A_i}}} + {f_{{A_i}}}\text{,}\begin{array}{*{20}{c}} {} & {} \end{array}(b)}\text{。} \end{array}} \right. $ | (2) |
The weights of indexes Cj, Ck, …Cp are j, k, …p[0, 1], and
The conformity of project Yi can be calculated by formula 2(a) firstly:
| $ \begin{array}{l} {W_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i}) = ({t_{ij}} + t_{ij}^*-1) \times{\omega _j} + \\ \quad \quad \quad \quad \quad \quad \ \ ({t_{ik}} + t_{ik}^*-1) \times{\omega _k} + ... + \\ \quad \quad \quad \quad \quad \quad \ \ ({t_{ip}} + t_{ip}^*-1) \times{\omega _p}\text{。} \end{array} $ | (3) |
| $ {W_{Cs}}({A_i}) = S[{t_{is}}, t_{is}^*] = ({t_{is}} + t_{is}^*-1) \text{。} $ | (4) |
Secondly conformity of project Yi is calculated by formula 2(b):
| $ \begin{array}{l} {T_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i}) = ({t_{ij}}-t_{ij}^* + 1) \times{\omega _j} + \\ \quad \quad \quad \quad \quad \quad \ \ ({t_{ik}}-t_{ik}^* + 1) \times{\omega _k} + ... + \\ \quad \quad \quad \quad \quad \quad \ \ ({t_{ip}}-t_{ip}^* + 1) \times{\omega _p}\text{。} \end{array} $ | (5) |
| $ {T_{Cs}}({A_i}) = H[{t_{is}}, t_{is}^*] = ({t_{is}}-t_{is}^* + 1) \text{。} $ | (6) |
Then the confidence interval of Yi is defined according to conformity of each index, as in formula (7) and (8) :
| $ \begin{array}{l} {R_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i}) = ({W_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i})-\frac{{1-{T_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i})}}{2}, \\ \quad \quad \quad \quad \quad \quad \ \ {W_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i}) + \frac{{1-{T_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i})}}{2})\text{。} \end{array} $ | (7) |
| $ \begin{array}{l} {R_{Cs}}({Y_i}) = ({W_{Cs}}({Y_i})-\frac{{1-{T_{Cs}}({Y_i})}}{2}, \\ \quad \quad \quad \quad \ {W_{Cs}}({Y_i}) + \frac{{1-{T_{Cs}}({Y_i})}}{2})\text{。} \end{array} $ | (8) |
Among the formulas above,
The membership confidence interval of project Yi calculated by formula (7) are as follows:
Then the weighting minimum, maximum and middle ranking functions are defined as in formula (9) , (10) and (11) :
| $ \begin{aligned} {R_{\min }}({Y_i}) = & \max ({W_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i})-\frac{{1-{T_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i})}}{2}, \\ & \displaystyle{W_{Cs}}({Y_i})-\frac{{1-{T_{Cs}}({Y_i})}}{2})\text{。} \end{aligned} $ | (9) |
| $ \begin{aligned} {R_{\max }}({Y_i}) = & \max ({W_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i}) + \frac{{1-{T_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i})}}{2}, \\ & \displaystyle{W_{Cs}}({Y_i}) + \frac{{1-{T_{Cs}}({Y_i})}}{2})\text{。} \end{aligned} $ | (10) |
| $ {R_{center}}({Y_i}) = \max ({W_{{ \cap _{l = j, k, ..., p}}{C_l}}}({Y_i}), {W_{Cs}}({Y_i}))\text{。} $ | (11) |
At last, according to the designer attitude towards risk, conservative designer use the maximum-minimum method, which is
|
|
Tab.2 Results of Vague evaluation |
Table 2 shows that, the final evaluation results of three methods are
For the comparison analysis, four other typical evaluation methods are chosen here to calculate the same problem: the linear weighted method, the analytic hierarchy process attended by multiple experts (DAHP), group decision method with consistency adjustment, the ideal point method (TOPSIS). Results of each method are shown in figure 6.
Figure 6 shows that, except the linear weighted method, results of every algorithm are basically the same, which determine project 4 is best and project 1 is worst. So every algorithm has fine accuracy that can express the real preference of experts. Among the algorithms above, DAHP, TOPSIS and Vague set method can clearly express the quality of each project, while others can only give the similar results, which can be a big interference for experts. Relative to Vague method, DAHP is subjective evaluation method, which is easily influenced by personal experience and preference of evaluation experts, While TOPSIS is objective evaluation method, which can not effectively utilize the experts’ personal understanding to fuzzy index. So neither the subjective nor objective method is suitable for problem researched here.

|
Fig. 6 Curve of decision-making comparison result |
Via introducing SA optimization algorithm and Vague evaluation algorithm to the mechanism of naval ship project integrated design, the overall process operation of project design has been completed effectively, and satisfied design result is obtained. Research in this paper shows that, by reasonable selection of operation parameters, SA multiple targets optimization algorithm, which obtained a series of optimal projects of each target for evaluation, can avoid the drawbacks of single target optimization algorithm and has the more rationality and feasibility. Meanwhile, the Vague evaluation can integrate effectively both the quantitative and qualitative indexes and obtain the accurate and reliable evaluation result. And the integrated design process researched in this paper can be a great orientation of naval ship project design, and can also be used in other parts of naval ship development.
| [1] | SHAO Kai-wen, MA Yun-yi. Concept of naval technology and design[M]. Beijing: National Defense Industry Press, 2005 : 10 -17. |
| [2] | BROWN A J, SALCEDO J. Multiple-objective genetic optimization in naval ship design[J]. Naval engineers journal , 2003, 115 (4) :49–61. |
| [3] | BROWN A J, TECH V, M. THOMAS M. Reengineering the naval ship concept design process[J].//Research to reality in ship systems engineering symposium., [Sl]:ASNE, 1998:3. |
| [4] | SUN Shi-nan. Modern aircraft carrier[M]. Shanghai: Shanghai Popular Science Press, 2000 : 1 -22. |
| [5] | CHEN Han-bin. TSP problem based on multiple groups of simulated annealing algorithm[D]. Jiang men:Wuyi University, 2013. |
| [6] | LI Jin-zhong, XIA Jie-wu, ZENG Xiao-hui, et al. Survey of multi-objective simulated annealing algorithm and its applications research multi targets annealing algorithm and its application[J]. Computer Engineering and Science , 2013, 35 (8) :77–88. |
| [7] | LI Rui-lan. Intelligent forecast and decision-making based on Vague set thoeryIntelligent forecast and decision making method based on Vague set[D]. Nan ning:Guangxi University, 2013. |
| [8] | XU Chang-lin, WEI Li-li. Vague set method of multi-criteria fuzzy decision making multi criteria fuzzy decision making method based on Vague set[J]. Systems Engineering-theory and & Practice , 2010, 30 (11) :2019–2025. |
| [9] | DELGADO M, HERRERA F, HERRERA-Viedma V E, et al. Combining numerical and linguistic information in group decision-making[J]. Information Sciences , 1998, 107 (1/4) :177–194. |
 2016, Vol. 38
2016, Vol. 38
