焊接是重要的材料加工方法,在船舶建造过程中广泛应用。焊接引起的残余变形和应力影响船舶建造的质量,预测焊接残余变形和应力是开展船舶建造精度控制的重要基础[1]。热弹塑性有限元方法能动态追踪焊接过程中应力应变过程和焊后的残余应力与变形[2],广泛应用于各类典型接头焊接问题的研究中。然而,高度非线性使得焊接数值模拟焊接过程极为耗时,难以适用于大型船体加筋板结构。为有效地减少热弹塑性有限元法的计算时间,蔡志鹏等[3]在高斯热源的基础上提出了段状热源模型,在保证输入功率相当的前提下,将焊缝分成若干段,每一段上同时作用高斯热源,热流密度沿焊缝方向分布均匀,垂直于焊缝方向则为高斯函数分布。相比于移动热源 Zhen CHEN等,段状热源在保证一定计算精度的前提下可以有效地缩短计算时间。SHEN Jichao[4]将 Shell/Solid 模型应用于角接接头的焊接模拟,对焊缝区域的 solid 和 shell 单元通过线性约束实现节点自由度的对应关系,由于大幅度降低了模型求解自由度,该模型在保证计算精度的同时有效地提高了计算效率。沈济超等[5]采用分段移动热源,在段内考虑时间效应,通过与试验测量值对比验证了该方法的高效性。
本文基于有限元分析软件 Abaqus ,将各加筋板划分为独立的静态子结构分别计算温度场,通过温度场映射有效提高温度场计算效率。通过对典型船体加筋板结构的焊接数值模拟,验证该方法的高效性和适用性。
1 问题的提出以船体加筋板结构为研究对象,几何尺寸如图 1 所示,其中水平板尺寸为 2 000 mm × 1 500 mm,厚度 12 mm;腹板尺寸为 2 000 mm × 150 mm,厚度 9 mm;面板尺寸为 2 000 mm × 80 mm,厚度 11 mm。结构共包含 6 条角焊缝,均位于腹板和水平板交界处,焊角高度为 6 mm;每条焊缝焊接方向沿 y 轴正向,焊接顺序为从左至右依次焊接,每条焊缝焊接完毕后均充分冷却。

|
图 1 船体加筋板几何尺寸 Fig. 1 Geometry of stiffened panel |
采用顺序耦合热弹塑性有限元法模拟加筋板焊接过程,首先通过热传导分析获得热源作用下结构的温度分布,然后将温度场以外载荷的形式施加到有限元模型上,计算结构的应力应变响应。对于图 1 所示加筋板结构,完整结构热弹塑性有限元模型的自由度数目多,对计算机资源要求高。根据船体结构重复性和对称性的特点,采用静态子结构方法和温度场映射技术求解加筋板结构温度场,可以有效提高计算效率。
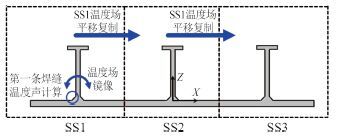
2 静态子结构方法与温度场映射 2.1 静态子结构焊接过程温度场的特点是热源附近和热影响区局部区域温度高、梯度大,随着距热源中心距离的增加,温度迅速降低[6]。根据焊接过程温度分布规律,在开展船体焊接过程温度场分析时,将各加筋板划分为独立的静态子结构分别进行计算。在进行子结构焊接过程温度场模拟时,不考虑其他结构的影响。若子结构的划分超过一定范围,在其边缘处温度的差异很小,不足以引起结构应力应变响应的明显差异。由于子结构模型自由度较完整结构大幅减少,温度场分析计算耗时显著降低。图 2 所示为船体加筋板结构 3 个静态子结构 SS1,SS2 和 SS3 的划分情况。
|
图 2 子结构和温度场映射 Fig. 2 Substructures and temperature mapping |
将船体加筋板整体模型划分为若干个子结构,分别进行焊接过程热传导分析。根据船体结构的特点,若各子结构尺寸和焊接条件完全相同,则对应位置的节点温度历程相同;并且,子结构由于自身结构的对称性,每条焊缝焊接完后均充分冷却,则分别焊接子结构两侧焊缝时对应的温度历程关于腹板中面对称。因此,各个子结构之间的温度场分布具有平移复制的特点,单个子结构的温度场具有对称镜像的特点。在计算得到一个子结构一条焊缝的温度场后,可分别通过温度场镜像和平移(见图 2)得到其他焊缝和子结构的温度场结果,进一步提高加筋板结构焊接温度场模拟的计算效率。温度场的镜像和平移程序由 Python 二次开发实现[9]。
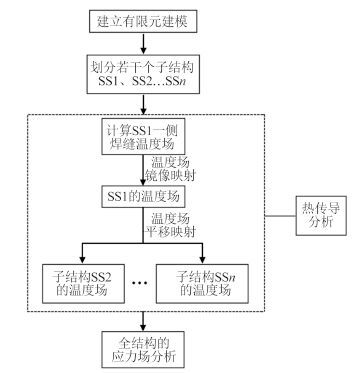
3 有限元数值模拟船体加筋板结构采用静态子结构和温度场映射方法进行焊接温度场数值模拟,与完整结构相比可极大地节省温度场计算时间。有限元计算流程如图 3 所示。
|
图 3 计算流程图 Fig. 3 Flowchart of analysis |
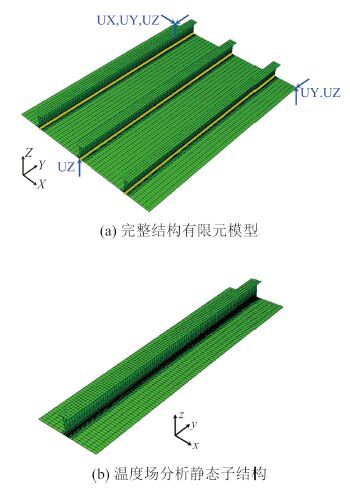
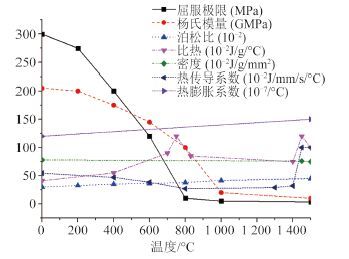
根据加筋板结构尺寸,建立有限元计算模型。采用 shell/solid 混合单元建模[4],热传导分析 shell 单元采用四节点矩形单元 DS4,沿厚度方向设置 5 个截面积分点,焊角采用 solid 单元 DC3D8,solid 单元和 shell 单元之间通过线性约束方程实现自由度约束。图 4(a)为完整结构的有限元模型,图 4(b)为温度场分析所采用的静态子结构有限元模型,在焊缝区域网格较密,最小单元尺寸为 5 mm × 2.25 mm,在远离焊缝区域网格尺寸逐渐增大,结构应力场分析和热传导分析网格划分相同。焊接参数及材料属性见文献[7],焊接采用 CO2 气体保护焊,焊接电流为 270 A,焊接电压为 29 V,焊接速度 6.67 mm/s,热效率为 0.8。材料为 SM400A 船用钢,杨氏模量、热膨胀系数、比热、热传导系数等物理量与温度的关系如图 5 所示。
|
图 4 计算有限元模型 Fig. 4 FE model |
|
图 5 材料属性 Fig. 5 Material properties |
热弹塑性有限元计算采用瞬时移动热源模型,热输入总能量包括母材表面施加高斯分布热源和焊脚施加均匀分布体热源两部分,其中高斯面热源的能量配比为 40%,均布体热源为 60%[8]。高斯热源的表达式为:
| $ q = \frac{{3Q}}{{\pi {r_a}^2}}\exp \left\{ {\frac{{ - 3{r^2}}}{{{r_a}^2}}} \right\}\text{。} $ | (1) |
式中:Q 为高斯热源总能量;ra为热源半径 6 mm;r 为焊件表面距热源中心的距离。
温度场计算的表面散热系数为 33 × 10-6W/(mm2·℃),环境温度为 20 ℃,焊接应力场计算中的边界条件如图 4 所示。
4 计算结果分析与讨论 4.1 静态子结构与完整结构计算对比为验证子结构温度场计算结果的准确性,对子结构 SS1 与船体加筋板完整结构焊接过程进行数值模拟。图 6 为子结构 SS1 的水平板边缘(即直线 x =-750 mm 和 x =-250 mm 处)上表面温度分布与完整结构相同位置的温度对比图。在焊接第 1 道焊缝 t = 200 s 时,热源经过的地方引起边缘温度值升高,而热源未到达处保持室温不变,且子结构 SS1 的自由边缘 x =-750 mm 处温度分布与完整结构对应位置几乎完全一致(见图 6(a));焊接完毕并冷却结束后结构的整体温度接近室温(见图 6(b))。

|
图 6 子结构边缘温度与完整结构温度对比图 Fig. 6 Temperature comparison between the edge of SS1 and overall structure |
子结构 SS1 中的第 2 道焊缝焊接过程温度场由第 1 道焊缝温度场镜像获得,而完整结构两道焊缝均由瞬时移动热源热传导非线性分析得到。在焊接第 2 道焊缝的过程中,选取对应加筋板 y = 500 mm 横截面水平板上的点 A,其温度历程如图 7 所示。显然,子结构通过温度场镜像映射得到的计算结果和全结构的计算结果非常接近,平均误差为 1.3%,仅在焊接开始时的温度值略有差异,但最大误差不超过 7.5%。这是由于第 1 道焊缝结束后结构并没有完全冷却至室温,而在对第 2 道焊缝进行温度场镜像映射时,给结构赋予了初始室温,导致了差异的产生。

|
图 7 点 A 的温度历程曲线 Fig. 7 Temperature history of point A |
采用子结构和完整结构进行加筋板焊接过程热传导分析,温度场计算结果差别很小。由于结构响应分析均采用相同的完整结构模型,因此 2 种模型计算的焊接变形和残余应力分析无明显差异。
本文所有的计算均在 DELL Precision 1700 工作站(3.2 G CPU,8 G 内存)上进行,采用完整结构计算第 1 和第 2 条焊缝温度场所用时间为 181.7 h,而采用静态子结构计算 SS1 中第 1 条焊缝温度场并结合温度场映射方法得到第 2 条焊缝温度场所用时间仅为 26.6 h,计算时间仅为原来的 14.6%,并且通过温度场映射获得其余子结构中焊缝的温度场所用时间仅为 3.2 h,计算时间显著减少。因此,采用静态子结构和温度场映射可以极大地提高计算效率。
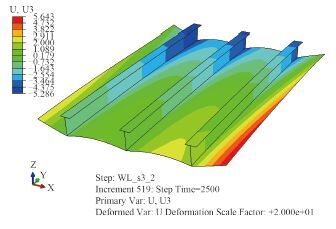
4.2 全结构焊接变形图 8 为船体加筋板结构焊接完成冷却后的残余变形云图。由图可见,水平板最大垂向变形出现在纵向自由边界处,板格间呈瘦马状变形。
|
图 8 船体加筋板整体变形云图 Fig. 8 Overall vertical deflection |
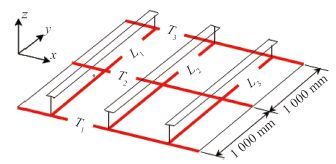
图 9 显示了船体加筋板典型纵向路径 L1,L2,L3 和横向路径 T1,T2,T3 的位置,以下将通过这 6 条路径上的变形和应力来分析加筋板的焊接变形和残余应力特征。
|
图 9 纵横路径的位置示意图 Fig. 9 Location of L1~T3 |
图 10 为焊接结束后,6 条纵横直线位置上的面外变形图。尽管结构中只有纵向焊缝,但整体结构纵向和横向均发生了弯曲,这主要是由于焊接过程引起了纵横 2 个方向材料收缩。图 10(a)为 T1~T3 位置焊接面外变形,反映了加强筋之间的局部面外变形和结构整体变形的叠加现象;图 10(b)为 L1~L3 位置加强筋沿焊缝方向的面外变形,3 根加强筋首尾端垂向位移差

|
图 10 结构的面外变形 Fig. 10 Vertical distortion |
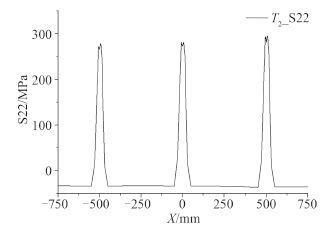
图 11 为加筋板在 T2 位置处水平板中面纵向残余应力分布图。由图可见,残余拉应力集中分布在焊缝附近区域,其大小在材料的屈服极限左右;而在远离焊缝处则迅速转变为压应力,分布均匀,大小约为-35 MPa,该压应力容易引起板的屈曲。虽然 3 根加筋板焊接顺序为自左向右依次进行,但纵向残余应力分布无明显焊接顺序效应,残余应力大小及分布主要取决于当前加强筋焊接热输入情况。
|
图 11 水平板中面在 T2 处的纵向残余应力 Fig. 11 Longitudinal residual stress at middle surface of plate at T2 |
图 12(a)、图 12(b)和图 12(c)分别为 3 根加强筋依次焊接完毕后,T2 位置处水平板的上表面横向残余应力变化情况。当第 1 根加强筋焊接完成时,横向残余拉应力在焊缝附近区域达到材料的屈服极限,在第1 和第 2 根加强筋之间水平板内均匀分布大小约为 50 MPa 的拉应力,靠近自由边一侧和第 2 根加强筋以外的水平板内应力几乎保持为 0 不变,如图 12(a)。当第 2 根加强筋焊接完成之后,焊缝附近横向残余拉应力达到材料屈服强度,第 1 和第 2 根加强筋之间拉应力量值有所提高,达到约 75 MPa;第 2 和第 3 根加强筋之间水平板约 50 MPa,如图 12(b)。整个加筋板焊接完成之后,水平板内的横向残余应力基本呈对称分布,如图 12(c)。

|
图 12 水平板上表面 T2 处的横向残余应力分布图 Fig. 12 Transverse residual stress at middle surface of plate at T2 |
1)通过静态子结构方法有效地降低了热传导分析的自由度,实现焊接数值模拟中热传导分析,并将其应用于船体多筋加筋板的焊接残余变形和应力的预报,在保证计算精度的同时,大幅度提高了计算效率。因此该方法可以应用于船体某些大型板架的焊接数值模拟。
2)船体板架的焊接会引起纵横 2 个方向的收缩,使结构产生双向弯曲,焊接顺序不对称还会引起板架的整体扭曲变形。
3)船体加筋板在焊缝附近,焊接纵向残余拉应力大小约为材料屈服极限,在远离焊缝区域残余应力迅速降低并转变为均匀分布的压应力。在焊接结束后,加筋板的水平板中横向残余应力基本呈对称分布,焊接顺序对板架的残余应力分布并无明显的影响效应。
| [1] |
周宏, 罗宇, 蒋志勇. 基于固有应变的船体总段船台合拢焊接变形预测研究[J]. 船舶力学 , 2013, 17 (10) :1153–1160.
ZHOU Hong, LUO Yu, JIANG Zhi-yong. Prediction of welding deformation of block construction of hull based on inherent strain methods[J]. Journal of Ship Mechanics , 2013, 17 (10) :1153–1160. |
| [2] |
徐东, 杨润党, 王文荣, 等. 船体结构焊接变形预测与控制技术研究进展[J]. 舰船科学技术 , 2010, 32 (1) :132–137.
XU Dong, YANG Run-dang, WANG Wen-rong, et al. Review on prediction and control welding distortion of ship structure[J]. Ship Science and Technology , 2010, 32 (1) :132–137. |
| [3] |
蔡志鹏, 赵海燕, 吴甦, 等. 串热源模型及其在焊接数值模拟中的应用[J]. 机械工程学报 , 2001, 37 (4) :25–28.
CAI Zhi-peng, ZHAO Hai-yan, WU Su, et al. Model of string heat source in welding numerical simulations[J]. Chinese Journal of Mechanical Engineering , 2001, 37 (4) :25–28. DOI:10.3901/JME.2001.04.025 |
| [4] | SHEN J C, CHEN Z. Welding simulation of fillet-welded joint using shell elements with section integration[J]. Journal of Materials Processing Technology , 2014, 214 (11) :2529–2536. DOI:10.1016/j.jmatprotec.2014.04.034 |
| [5] |
沈济超, 陈震, 罗宇. 船舶T型接头分段移动热源焊接模拟[J]. 中国造船 , 2014, 55 (4) :66–73.
SHEN Ji-chao, CHEN Zhen, LUO Yu. Welding simulation of T-shape joint in hull by segmented moving heat source[J]. Shipbuilding of China , 2014, 55 (4) :66–73. |
| [6] |
刘川, 张建勋. 基于动态子结构的三维焊接残余应力变形数值模拟[J]. 焊接学报 , 2008, 29 (4) :21–24.
LIU Chuan, ZHANG Jian-xun. Numerical simulation of welding stresses and distortions based on 3D dynamic substructure method[J]. Transactions of the China Welding Institution , 2008, 29 (4) :21–24. |
| [7] | DENG D A, LIANG W, MURAKAWA H. Determination of welding deformation in fillet-welded joint by means of numerical simulation and comparison with experimental measurements[J]. Journal of Materials Processing Technology , 2007, 183 (2/3) :219–225. |
| [8] | PARDO E, WECKMAN D C. Prediction of weld pool and reinforcement dimensions of GMA welds using a finite-element model[J]. Metallurgical Transactions B , 1989, 20 (6) :937–947. DOI:10.1007/BF02670199 |
| [9] |
曹金凤, 王旭春, 孔亮.
Python语言在Abaqus中的应用[M]. 北京: 机械工业出版社, 2011 : 202 -229.
CAO Jin-feng, WANG Xu-chun, KONG Liang. The application of Python in Abaqus[M]. Beijing: China Machine Press, 2011 : 202 -229. |
 2016, Vol. 38
2016, Vol. 38
