导管螺旋桨与普通螺旋桨的不同之处在于其桨的外围多了 1 个套筒,该套筒的纵剖面为机翼型或折角型[1],此为导管螺旋桨的导管。增加导管后,螺旋桨与导管成为一个整体,其周围的流场与未增加导管时大不相同[2]。对于加速型导管来说,首先可使桨盘面处的水流加速,使螺旋桨工作在较大的速度场,从而提高桨的效率[3];另一方面,由于叶稍和导管的间隙很小,由叶面和叶背的压力差引起的绕流大大减小,其能量损头也就减小。因此加速导管螺旋桨具有效率高、推力大、在风浪中的性能较好等特点[4]。
螺旋桨型值表的桨叶几何模型建立及计算域空间网格离散是其水动力性能 CFD 预报的2个前提步骤[5]。为了比较准确地刻画桨叶导边、随边、叶稍及叶尖等几何细节部分,桨叶几何通常都是在 CAD 软件中完成,比如 UG。网格划分通常分为六面体结构化网格和四面体非结构化网格。从计算机资源利用率、网格数值耗散大小还是桨叶几何细节的刻画来说,六面体结构化网格优于四面体非结构化网格[6-8]。上述观点成立的前提是网格划分及拓扑结构要合理,这是使用软件进行求解的核心技术所在[9]。
陈宁、赖海清等采用图谱估算方法对综合舵桨系统的导管螺旋桨水动力性能进行计算和研究,并结合导管螺旋桨的敞水试验进行验证,将计算值与实验值的误差控制在 11% 以内[10]。
1 数学模型与计算方法螺旋桨保持一定的转速在均匀流体中旋转,视为桨在轴向静止,假定其周围为旋转水域,螺旋桨与之保持相对静止。本研究采用不可压缩流体 RANS 方程作为求解旋转流场特性的控制方程。
质量方程:
| $ \frac{{\partial {{\rm{u}}_{\rm{i}}}}}{{\partial {{\rm{x}}_{\rm{i}}}}} = 0\text{;} $ | (1) |
动量方程
| $ \begin{array}{l} \displaystyle\frac{\partial }{{\partial {\rm{t}}}}\left( {\rho {u_{\rm{i}}}} \right) + \frac{\partial }{{\partial {x_{\rm{j}}}}}\left( {\rho {{\rm{u}}_{\rm{i}}}{{\rm{u}}_{\rm{j}}}} \right) =-\frac{\partial }{{\partial {{\rm{x}}_i}}} + \\ [10pt] \quad\quad\quad\quad \displaystyle\frac{\partial }{{\partial {{\rm{x}}_j}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {{\rm{x}}_j}}}-\overline {\rho u_i^{'}u_j^{'}} } \right) + \rho {g_i}\text{。} \end{array} $ | (2) |
式中:t 为时间;ρ 为密度;μ 为流体的动力粘性系数;ui 和 uj 为速度分量时均值;P 为静压;xi 和 xj 分别为 i 和 j 方向上的位置坐标;gi 为单位质量的重力;
控制方程为不可压缩流体的连续性方程和 RANS 方程,其张量形式为:
| $ \frac{{\partial \overline {{u_i}} }}{{\partial {x_i}}} = 0\text{,} $ | (3) |
| $ \rho \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \rho \overline {{u_j}} \frac{{\partial \overline {{u_i}} }}{{\partial xj}} = \rho \overline {{F_i}}-\frac{{\partial \overline P }}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}}-\overline {\rho {u_i}{u_j}} } \right)\text{。} $ | (4) |
湍流模型的选取主要依靠以下几点:流体是否可压;建立特殊可行的问题;精度要求;计算机能力;时间限制。没有一个湍流模型对于所有问题是通用的,本文采取 SST k-w 湍流模型对导管桨敞水性能进行预报。
2 网格划分及边界条件设定 2.1 实尺度模型的建立及网格划分设定计算选用右旋螺旋桨和 19 A 导管,尺寸如表 1 所示。
|
|
表 1 螺旋桨基本参数(右旋) Tab.1 The basic parameters of propeller(right hand) |
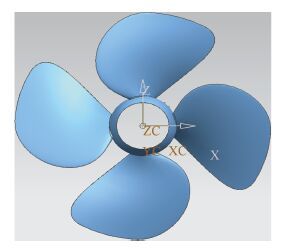
将螺旋桨及导管的型值表录入 Excel 表中生成三维坐标再导入到 UG 三维建模软件生成三维几何模型如图 1~ 图 3 所示,文中模型均为实尺度模型。计算域来流方向距离桨盘面 3 倍螺旋桨直径,出流方向距离桨盘面 5 倍螺旋桨直径,计算域直径为 5 倍桨直径的圆筒。
|
图 1 桨叶几何模型 Fig. 1 The model of the blade |

|
图 2 导管几何模型 Fig. 2 The model of the ducted |
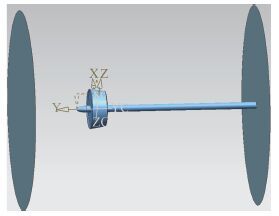
|
图 3 计算外域几何模型 Fig. 3 The model of Out-domain |
网格的划分是在 ICEM CFD 软件中进行。计算域分为内外两个域,内部流场计算域与外部流场计算域网格分开划分。内域由于桨叶形状比较复杂不利于网格划分因此采用非结构化网格来填充,网格数为 960 万,节点数为 306 万,如图 4 所示。外域因为结构比较简单规整因此使用结构化网格,网格数与节点数大约为 310 万,如图 5 所示。

|
图 4 内部计算域网格划分 Fig. 4 The meshing of Internal domain |
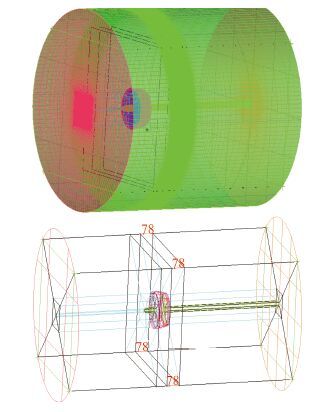
|
图 5 外部计算域网格划分及拓扑结构 Fig. 5 External meshing calculation domain and topology |
导管桨敞水性能计算中,来流方向边界设定为速度入口,速度给定不变;出口边界定义为压力出口边界;圆筒表面设为无滑移壁面;并将粗糙度设为 30 μm;旋转水域绕轴以 316 r/min 的角速度旋转,通过改变进流速度来实现不同进速系数;使用有限体积法离散控制方程和湍流模式,对流项和扩散项的离散采用高阶求解模式;收敛判据残差设为 1E-06。
3 敞水模拟计算结果分析进速系数分别取 0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,螺旋桨转速固定为 316 r/min。通过 CFX 模拟计算,得出不同进速系数下的螺旋桨推力 KT、导管推力与螺旋桨力矩 KQ,根据相应公式可计算出相应值。
进速系数:
| $ J = \frac{{{V_A}}}{{nD}}\text{;} $ | (5) |
推力系数:
| $ {K_T} = \frac{T}{{\rho {n^2}{D^4}}}\text{;} $ | (6) |
力矩系数:
| $ {K_Q} = \frac{Q}{{\rho {n^2}{D^5}}}\text{;} $ | (7) |
螺旋桨效率:
| $ \begin{aligned} \displaystyle{\eta _o} = & \frac{{T{V_A}}}{{2\pi nQ}} = \frac{{{K_T}\rho {n^2}{D^4}{V_A}}}{{2\pi n{K_Q}\rho {n^2}{D^5}}} = \\ & \displaystyle\frac{{{K_T}}}{{{K_Q}}} \cdot \frac{{{V_A}}}{{2\pi nQ}} = \frac{{{K_T}}}{{{K_Q}}} \cdot \frac{J}{{2\pi }} \end{aligned} $ | (8) |
式中:T 为推力;Q 为力矩;ρ 为水的密度;n 为螺旋桨转速;D 为螺旋桨直径。
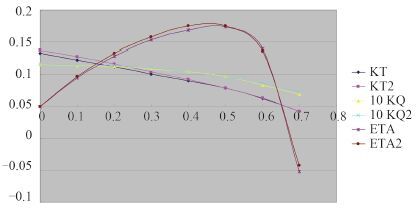
根据各个进速系数的计算值和实验值,得出如表 2 所示的误差分析结果。计算值与试验值的拟合比较如图 6 所示。图中KT,10 KQ 和 ETA 分别为推力系数、力矩系数和效率值的计算值;KT2,10 KQ2 和 ETA2 分别为推力系数、力矩系数和效率值的参考值。
|
|
表 2 结果比较 Tab.2 Comparison results |
|
图 6 敞水性能计算值与试验值的对比 Fig. 6 Comparison between calculations and test results of open-water performance |
由图 6可知,推力系数 KT、力矩系数 KQ 及敞水效率 ηo 的计算结果与试验结果变化趋势基本一致,从整体来看模拟计算效果较好。分析误差产生的原因,主要是计算模拟模型与实物存在一定的误差,在模拟状态中都是属于理想状态,这在实际的工程试验中是不可能达到的;另一方面,在进速系数比较大时,其推力系数、力矩系数的绝对值都比较小,在绝对误差不大的情况下相对误差也可能较大。对于内域的网格划分都使用非结构化网格,虽然生成网格比较方便,但网格质量没有结构化网格好,而网格质量的好坏很大程度上决定了计算结果的准确性。
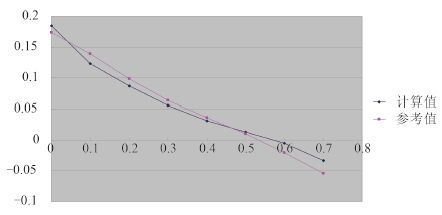
由图 7 可看出,随着进速系数的增大,导管推力不断变小,并且在 0.6 和 0.7 处导管产生的并不是推力而是阻力。
|
图 7 导管推力系数(KTD)计算值与试验值的对比 Fig. 7 Comparison between calculations and test results of KTD |
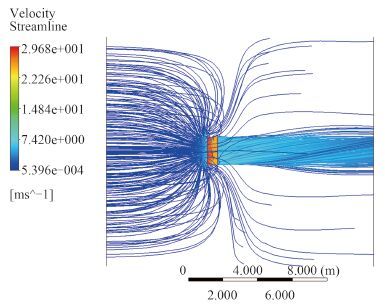
对于系泊工况即进速系数 J = 0 时,因为其交界面与边界条件设置与其他工况不同,所以应特殊考虑。图 8 为系泊工况流线图。
|
图 8 系泊工况流线图 Fig. 8 The stream lines of the mooring conditions |
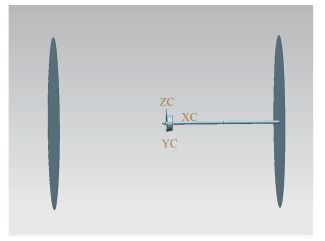
该桨后方的流线出现异常情况,初步猜想是因为出口边界与桨叶间的距离太近的原因,因此接下来对其外部计算域扩大。将四周边界设为开放边界 opening,另一方面将外域扩大,前后端都为 10 倍的桨盘直径,径向为 12 倍桨盘直径,且四周边界都设为 opening。改进几何如图 9所示。
|
图 9 系泊工况外域几何 Fig. 9 The out-domain of mooring conditions |
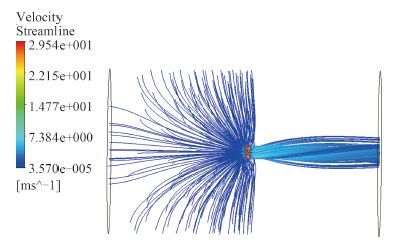
外域扩大后其网格数达到 620 万,节点数为 610 万。计算流线结果如图 10 所示。
|
图 10 系泊工况改进后流线图 Fig. 10 The stream lines of the mooring conditions after improvement |
从流线图及结果对比可看出,将计算域扩大后,流线更符合实际流动,也没有从桨叶后方的来流进入导管区域。对照表 3和表 4可看出,推力系数计算结果也更加精确,误差变小。因此按上面方式扩大计算域能更加准确地刻画系泊工况下导管桨的工作情况。
|
|
表 3 系泊工况改进前结果比较 Tab.3 Results compared before the improvement of mooring conditions |
|
|
表 4 系泊工况改进后结果比较 Tab.4 Results compared after the improvement of mooring conditions |
本文采用数值模拟方法研究实尺度导管螺旋桨的敞水性能,对某右旋螺旋桨和 19 A 导管桨组成的导管螺旋桨进行了敞水计算,通过实验结果验证了数值计算方法的可靠性和准确性,并对系泊工况进行一定探索。得到以下结论:
1) 利用本文中的实尺度模型网格划分及边界条件设置,进速系数在 0.6 以内时,推力系数误差绝对值在 8% 以内,力矩系数误差绝对值在 2.5% 以内,效率误差绝对值在 6% 以内。考虑到该导管桨最高效率工作点在 0.4 ~ 0.5 之间,因此该方法可以比较准确的刻画出该类导管螺旋桨的敞水性能曲线。
2)不同航速下,导管作用并不相同。在低速工况下,导管可以产生较大的推力,但在高速工况下产生的则是阻力。
3)针对特殊的系泊工况,通过对边界条件设置的改进,使得计算模拟结果更加的可靠,流线也更加符合物理规律。
4) 导管推力系数在有些进速点误差较大。
| [1] |
盛振邦, 刘应中.
船舶原理[M]. 上海: 上海交通大学出版社, 2009 : 177 -188.
SHENG Zhen-Bang, LIU Ying-zhong. Ship principle[M]. Shanghai: Shanghai Jiao-tong University Press, 2009 : 177 -188. |
| [2] |
解学参, 黄胜, 胡健, 等. 导管桨内部流场的数值计算[J]. 哈尔滨工程大学学报 , 2009, 30 (1) :7–12.
XIE Xue-shen, HUANG Sheng, HU Jian, et al. Inner flow field calculations for ducted propellers[J]. Journal of Harbin Engineering University , 2009, 30 (1) :7–12. |
| [3] |
黄建伟, 张克危. 导管桨的流动分析与性能预测[J]. 舰船科学技术 , 2004, 26 (S) :51–55.
HUANG Jian-wei, ZHANG Ke-wei. Flow analysis and performance perdiction of ducted propeller[J]. Ship Science and Technology , 2004, 26 (S) :51–55. |
| [4] |
胡健, 马骋, 黄胜, 等. 导管对螺旋桨水动力性能的影响[J]. 武汉理工大学学报(交通科学与工程版) , 2009, 33 (5) :992–995.
HU Jian, MA Cheng, HUANG Sheng, et al. Influence of duct on hydrodynamics of propelle[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering) , 2009, 33 (5) :992–995. |
| [5] |
杨琼方, 郭薇, 王永生, 等. 螺旋桨水动力性能CFD预报中预处理的程序化实现[J]. 船舶力学 , 2012, 16 (4) :375–382.
YANG Qiong-fang, GUO Wei, WANG Yong-sheng, et al. Procedural realization of pre-operation in CFD prediction of propeller hydrodynamics[J]. Journal of Ship Mechanics , 2012, 16 (4) :375–382. |
| [6] | BERCHICHE N, JANSON C E. Grid influence on the propeller open-water performance and flow field[J]. Ship Technology Research , 2008, 55 :87–96. DOI:10.1179/str.2008.55.2.005 |
| [7] |
孙铭泽. 螺旋桨敞水性能RANS模拟中网格因素的影响分析[D]. 武汉:海军工程大学, 2009.
SUN Ming-ze. Propeller open water performance RANS simulation grid factors analysis[D]. Wuhan:Naval Engineering University, 2009. |
| [8] | HSIAO C T, CHAHINE G L. Tip vortex cavitation inception Scaling for an open marine propeller[C]//27th symposium on naval hydrodynamics[D]. Seoul, Korea:Curran Associates, Inc., 2008. |
| [9] |
李卉, 邱磊. 螺旋桨水动力性能研究进展[J]. 舰船科学技术 , 2011, 33 (12) :3–8.
LI Hui, QIU Lei. Development and present situation of the propeller hydrodynamic performance[J]. Ship Science and Technology , 2011, 33 (12) :3–8. |
| [10] |
陈宁, 赖海清. 导管螺旋桨设计和水动力性能分析[J]. 造船技术 , 2014 (3) :10–13.
CHEN Ning, LAI Hai-qing. Design and hydrodynamic performance analysis for ducted propeller[J]. Marine Technology , 2014 (3) :10–13. |
 2016, Vol. 38
2016, Vol. 38
