随着工业技术的发展和海洋资源开发的需要,船舶不断向高速化和大型化发展,因此,船舶发生砰击现象的概率也越来越高。砰击的作用是瞬态的,严重的砰击一方面会使冲击区域承受巨大压力,造成局部结构破坏;另一方面,会引起整个船体的振颤,使船体中部强力甲板及船底板产生瞬间高应力,由此产生的振动弯矩与波浪低频弯矩迭加时,会破坏船体的总纵强度。调查数据表明,历史上 10%~12% 的海损事故由剧烈的砰击引起[1]。1980-1981 年冬季,Onomichi-maru 号散货船以 5.25 kn 航速在 8 级海况的 beaufort 海域航行,其船首前甲板突然发生超过 5°向上弯曲,随后持续振荡约 2 h 后断裂脱落,大约 85%船体的其他部分 4 天后也相继沉没。事后调查发现:恶劣海况使该船超过 L/10 区域的船体发生砰击,砰击载荷的频繁作用使船体主要构件遭受到严重的低周疲劳,甲板处首先发生弯曲破坏并沿船体横向产生大的裂纹而断裂,从而引发整船的崩溃,最终导致沉没[2]。1994 年,Estonia 号滚装船在波罗的海的风浪中航行,其罩壳式首门的锁紧和定位装置被波浪砰击载荷打断,导致船舶大量进水而沉没,900 多名乘客和船员丧生[3]。
国内外对砰击问题的研究主要是从理论、实验及数值仿真 3 个方面展开。1929 年,Von Karman[4]最早开始对砰击问题展开研究,将水上飞机的降落过程简化为二维楔形体砰击水面的理论模型。Wagner[5]在 Von Karman 的基础上,考虑到了结构冲击时的液面升高现象,并且引入了湿表面的概念。Ochi 和 Motter[6]通过分析和总结上百个船模在波浪中的砰击试验数据,提出了在船舶剖面底部的砰击压力公式。Chuang[7-9]通过对刚性平底结构、斜升角为 1°~15°的楔形体以及轴对称锥体等结构进行实验,并且给出了平底结构砰击压力峰值经验公式以及不同斜升角的楔形体、三维轴对称锥体的砰击压力回归公式。Zhao 和 Faltinsen[10]提出了使用非线性边界元方法求解任意形状的二维结构的入水问题,并将入水角的计算范围扩展至 4 °~81 °,其计算结果与自相似法和渐进展开法的结果相比较,取得了良好的一致。陈震和肖熙[11-13]利用 MSC.Dytran 软件对二维平底、二维楔形体、U型船体剖面和球鼻首剖面以及三维椭球形刚性结构入水问题建立了有限元模型,并利用仿真结果对船舶的砰击问题进行多方面的研究。张于维和王志东等[14]利用 Fluent 仿真软件对二维楔形体的入水砰击问题进行了数值计算,对自由液面变化、砰击压力系数以及砰击的垂向力进行了分析研究。
砰击具有瞬时性和高度非线性的特点,想要在理论上建立气-液-固相耦合的模型十分困难,而且由于设备精度要求高、耗资巨大等原因,开展砰击试验也相对困难。因此,通过数值仿真方法进行气-液-固相耦合的砰击特性及载荷预报方法研究显得尤为重要。本文基于水动力学软件 Fine/Marine,充分考虑耦合作用的影响,对具有不同斜升角的楔形结构的砰击特性进行了仿真分析,同时,比较了不同斜升角及不同入水速度对砰击载荷的影响。
1 砰击压力峰值理论计算方法 1.1 经典理论计算方法 Von Karman [4]将水上飞机的降落过程简化为二维楔形体砰击水面的模型。设斜升角
| $ {P_{\max }} = \frac{1}{2}\rho {V^2}\frac{\pi }{{\tan \beta }} \text{。} $ | (1) |
这种方法对于具有较大倾角的结构,计算结果与实际较为接近;但当倾角接近于 0 时,砰击压力将趋于无穷大,与实际不符。
Wagner [5]考虑到了结构冲击时液面的升高现象,引入了湿表面的概念。设二维楔形刚体以等速入水,按浸湿半宽的“平板拟合”势流求解,在楔形体浸湿半宽的边缘,接近喷溅根部处出现的最大压力为:
| $ {P_{\max }} = \frac{1}{2}\rho {V^2}\left( {1 + \frac{{{\pi ^2}}}{{4{{\tan }^2}\beta }}} \right) \text{。} $ | (2) |
虽然 Wagner 理论求出的砰击压力在平板边缘具有奇异性,但仍成为后人研究砰击问题的基础理论。
Ochi 和 Motter[6]通过分析和总结上百个船模在波浪中的砰击试验数据,提出了在船舶剖面底部的砰击压力公式,整理可得:
| $ P = K \cdot {V^2} \text{。} $ | (3) |
式中:K 为砰击压力系数;V 为结构入水冲击瞬时速度。
1.2 砰击压力峰值系数的比较由于砰击问题的复杂性,人们在研究砰击时通常将其进行不同程度的简化,得到砰击压力的预报方法。也正是由于这个原因,各种预报方法的计算效率和计算结构有很大差别。但是,几乎所有实验研究均表明,砰击压力 P 与入水冲击瞬时速度 V 之间的关系如式(3)。由此可以看出,砰击压力的计算主要取决于入水冲击瞬时速度 V 的确定和砰击压力系数 K 的选取[15]。
根据式(1)和式(2)分别得出 Von Karman 和 Wagner 理论计算出的 K 值:
| $ \text{VonKarman}:K=\frac{{{P}_{\max }}}{{{V}^{2}}}=\frac{\rho \pi }{2\tan \beta }; $ | (4) |
| $ \begin{aligned} {\text{Wagner}}: K = \frac{{{P_{\max }}}}{{{V^2}}} = \rho \left[{\frac{1}{2} + \frac{{{\pi ^2}}}{{8{{\tan }^2}\beta }}} \right] \text{。} \end{aligned} $ | (5) |
由式(4)和式(5)可看出:Von Karman 和 Wagner 理论都有一定的适用范围,在
英国劳氏军规(NSR)[16]在 Ochi 和 Motter 理论基础上使用直接计算方法,给出了砰击载荷的计算公式。该方法可以计算出平均瞬时冲击压力,并利用动态压力系数将其转换为等效的静态载荷,由此方法确定的砰击压力系数 K(kPa/m2)为:
| $ K = \left\{ \begin{array}{l} \displaystyle \frac{\pi }{{2\tan \beta }} ,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \beta \geqslant {10^ \circ },\\ 141{\rm{-}}\tan (2\beta )) ,\ \ \ \ \ \ \beta < {10^ \circ } \text{。}\\ \end{array} \right. $ | (6) |
我国国家军用标准《水面舰艇结构设计计算方法》(GJB/Z 119-99)[17]中,规定了舰船首端局部结构设计时的砰击压力计算公式和相关计算曲线,明确了砰击压力峰值与船波相对速度的平方有关,其比例系数 K 取决于横剖面在砰击位置的斜升角
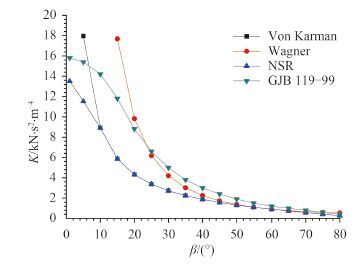
|
图 1
理论和规范中K~ |
采用船舶水动力分析软件 FineMarine 对楔形体模型进行计算和分析。首先,建立斜升角为 10°,20°,30°,40°,长 1 m,宽 0.5 m 的楔形体几何模型(质量为 50 kg),如图 2 所示。
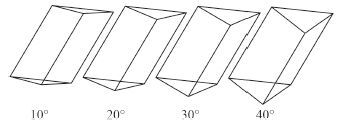
|
图 2 几何模型 Fig. 2 Geometric models |
由于楔形体左右对称,为节省计算时间,取一半模型进行网格划分。在网格划分过程中,为确保网格质量及网格的合理分布,在自由液面处以及楔形体与水面之间设置网格加密区,实现对自由液面的精确捕捉。以斜升角为 30 ° 的楔形体为例,建立有限元模型如图 3 所示。
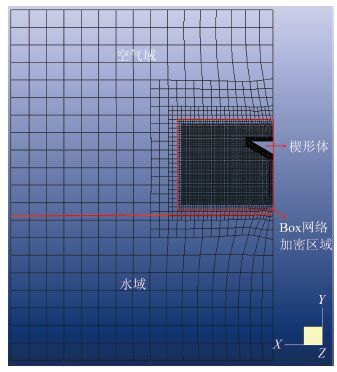
|
图 3 有限元模型 Fig. 3 Finite element model |
为充分反应结构砰击响应,同时考虑结构的对称特征,针对斜升角为 30 ° 的楔形体测点布置如图 4 所示:沿楔形体底面向上分布,水平间距为 50 mm(实际监测时,P5 稍往下偏移)。其他斜升角度的楔形体测点分布与之相同。

|
图 4 测点分布(单位:mm) Fig. 4 Distribution of measuring points |
在进行有限元计算时,不同斜升角的楔形体分别以 1 m/s,2 m/s,3 m/s,4 m/s,5 m/s 的速度从距离水面 0.02 m 的高度向水面冲击。
由于冲击过程非常短暂,尚未形成湍流,因此选择层流模式进行计算,并设置相应的边界条件:实体边界默认为无滑移壁面;计算域的上下表面设置为指定压力条件;其他边界条件设置为远场。在体的运动过程中,除了垂直方向上设置为求解运动外,其他方向上均固定。网格的变形形式选择刚性变形。
3.2 网格自适应技术Fine/Marine 的自由液面网格自适应准则,指的是网格只在自由液面附近即气-水掺混的区域进行网格自适应:细化或粗化。这种方法对于破碎波的自由演化等复杂自由液面的高精度预报问题可以实现合理的网格布局、减小网格总量、提高计算效率。本文采用的细化标准是自由液面张量标准,它类似于自由液面定向标准,只是在计算缓冲层时会稍有不同,在泡沫和破波区域的细化次数更少,适用于非稳定流的计算,如图 5 所示。

|
图 5 自由液面张量标准 Fig. 5 Free surface tensor criterion |
由于结构冲击时,自由液面的变化快速且剧烈,因此时间步的确定采用自适应库郎特数法则,即时间步是预先未知的,在每一个时间步上自适应至目标库郎特数(本文选取 C0=0.3)。这种方法不同于等时间步长的计算法则,它可以根据砰击的瞬时情况调整时间步长,从而有效捕捉冲击瞬间自由液面处的动态变化情况。
4 计算结果分析及结论 4.1 计算结果分析将模型提交计算,得到各测点在不同速度、不同斜升角下的砰击压力变化规律以及砰击压力系数值与理论值的对比结果。通过分析计算结果,验证了预报方法的可靠性。
4.1.1 不同速度下的砰击压力及峰值以斜升角为 30°的楔形体为例,在初始速度 V0(初始速度 V0 不同于结构入水冲击瞬时速度 V)分别为 1 m/s,2 m/s,3 m/s,4 m/s,5 m/s 时,从距离水面 0.02 m 的位置向水面冲击,得到各测点的砰击压力如图 6 所示。
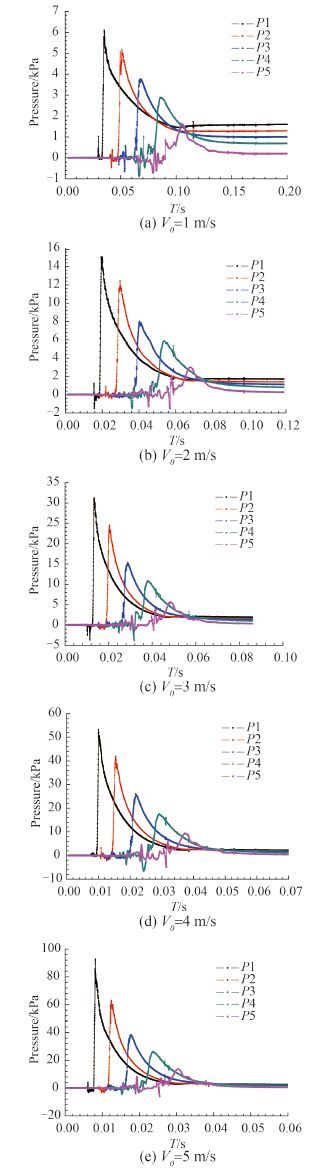
|
图 6 不同速度下的砰击压力曲线 Fig. 6 Slamming pressure curves of different speed |
从图中可看出,由于楔形体从距离水面 0.02 m 高度位置以某一速度下落,因此,从空气到刚接触水面的瞬间,楔形体仅受到空气阻力的作用,且空气阻力很小,可以忽略不计。随着时间的推移,在楔形体垂直下落的过程中,P1 ~ P5 测点相继受到水面冲击,在冲击的瞬间各测点均出现明显的砰击压力峰值,且从 P1 ~ P5 砰击压力峰值逐渐减小。这是由于气-液的耦合作用对楔形体产生了很大的阻力,使得楔形体的垂向速度减缓,进而导致砰击压力峰值逐渐减小。此外,对比图 6(a)~ 图 6(e)可以发现,在斜升角相同的情况下,随着入水速度的增大,砰击压力及峰值均明显增大。
4.1.2 不同斜升角下的砰击压力及峰值从图 7 可以看出,在本文研究的角度范围内,当入水冲击速度相同时,砰击压力及峰值随着斜升角的增大而减小。在图 7(a)中,P1 ~ P5 测点的砰击压力峰值先增大后减小,这是由于楔形体在入水过程中,水面抬升及射流现象引起的。这种现象在斜升角为 10°比较明显,而在斜升角为 20°,30°,40°时,P1 ~ P5 测点的砰击压力及峰值仍呈现逐渐减小的趋势,这说明在斜升角较小时,射流现象比较明显,而当斜升角超过一定范围后,射流现象不明显。

|
图 7 不同斜升角楔形体砰击压力 Fig. 7 Slamming pressure of different bottom angle of wedges |
图 8 将本文计算得到的砰击压力峰值系数 K 与 Wagner 理论及国家军用标准 GJB/Z 119-99 中得出的 K 值相比较,可以发现在不同速度下计算所得的 K 值基本介于 Wagner 理论和 GJB/Z 119-99 之间,且相差不大。因此,本文的计算结果可靠。
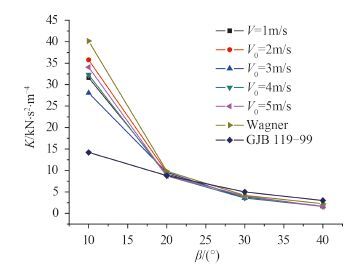
|
图 8 砰击压力峰值 K 系数与理论值对比 Fig. 8 Comparison between peak slamming pressure coefficient K and the theoretical value |
本文利用水动力学软件 FineMarine,针对不同斜升角二维楔形体结构的砰击问题展开仿真研究。通过仿真计算,分析了不同速度及不同斜升角度对楔形体的砰击压力及峰值的影响规律,得出了以下结论:
1)二维楔形体以某一速度冲击水面,在速度达到最大值的瞬间,出现砰击压力峰值。在斜升角相同时,随着入水速度的增大,砰击压力及峰值明显增大。
2)在一定范围内,楔形体的砰击压力及其峰值随着斜升角的增大而减小。在斜升角较小时,砰击压力峰值从 P1 ~ P5 先增大后减小,说明砰击压力峰值会受到水面抬升及射流的影响,而在斜升角较大时,从 P1 ~ P5 的砰击压力峰值逐渐减小,表明射流的影响不明显。
| [1] | DAIDOLA J C, MISHKEVICH V. Hydrodynamic impact on displacement ship hulls:An assessment of the state of the art, SSC-385A[RC]. Ship Structure Committee SSC-385A, 1995. |
| [2] | BISHOP R E, PRICE W G, TAMARAI P. The failure of the Onomichi-maru[R]. Naval Architect, 1985, 3:141-142. |
| [3] | SAMES P C, KAPSENBERG G K, COARRIGNAN P. Prediction of bow door loads in extreme wave conditions[C]//Royal institution of naval architects international conference, of design and operation for abnormal conditions Ⅱ:Prediction of bow door loads in extreme wave conditions. London, UK:Royal Institution of Naval Architects, London, UK, 2001. |
| [4] | VON KáARMáAN T. The impact ofn seaplane floats during landing:NACA technical note 321[R]. Washington, DC:National Advisory Committee for Aeronautics, Technical Memorandum 1929, 321:2-8. |
| [5] | WAGNER H. Über stoß-und gleitvorgänge an der oberfläche von flüssigkeiten[J]. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift Für Angewandte Mathematik und Mechanik , 1932, 12 (4) :192–215. |
| [6] | OCHI M K, MOTTER L E. Prediction of slamming characteristics and hull responses for ship design[CJ].//Annual meeting of SNAMETransactions. New York:SNAME, 1973, 81:144-177. |
| [7] | CHUANG S L. Experiments on flat-bottom slamming[J]. Journal of Ship Research , 1966, 10 (1) :10–27. |
| [8] | CHUANG S L. Experiments on slamming of wedges-shaped bodies[J]. Journal of Ship Research , 1967, 112 (3) :190–198. |
| [9] | CHUANG S L, MILES D T. Drop tests of cones to investigate the three-dimensional effects of slamming:, NSRDC Report 3453[R]. Fort Belvoir, VA:Defense Technical Information CenterNSRDC Report 3453, 1971. |
| [10] | ZHAO R, FALTINSEN OM. Water entry of two-dimensional bodies[J]. Journal of Fluid Mechanics , 1993, 246 :593–612. DOI:10.1017/S002211209300028X |
| [11] |
陈震, 肖熙. 平底结构砰击压力的分布[J]. 中国造船 , 2005, 46 (4) :97–103.
CHEN Zhen, XIAO Xi. The distribution of slamming pressure on Flat-Bottom structure[J]. Ship Building of China , 2005, 46 (4) :97–103. |
| [12] |
陈震. 海洋结构物入水砰击载荷与响应研究[D]. 上海:上海交通大学, 2005.
CHEN Zhen. Study on slamming loads and responses of ocean structure[D]. Shanghai:Shanghai Jiaotong University, 2005. |
| [13] |
陈震, 肖熙. 平底结构砰击压力峰值分析[J]. 上海交通大学学报 , 2006, 40 (6) :983–987.
CHEN Zhen, XIAO Xi. Analysis about the slamming pressure peak value on a flat-bottom structure[J]. Journal of Shanghai Jiaotong University , 2006, 40 (6) :983–987. |
| [14] |
张于维, 王志东, 晋文菊, 等. 二维楔形体砰击载荷研究[J]. 中国舰船研究 , 2010, 5 (3) :34–37.
ZHANG Yu-wei, WANG Zhi-dong, JIN Wen-ju, et al. Numerical simulation on slamming load of two dimensional wedge-shaped section[J]. Chinese Journal of Ship Research , 2010, 5 (3) :34–37. |
| [15] |
王辉. 船体结构局部强度设计中的砰击载荷确定方法[J]. 中国造船 , 2010, 51 (2) :68–77.
WANG Hui. Slamming load determination in local structure design of ships[J]. Ship Building of China , 2010, 51 (2) :68–77. |
| [16] | Lloyd's Register. Rules and regulations for the classification of naval ships[S]. London:Lloyd's Register, 2015:578-580. |
| [17] |
中国船舶工业总公司中华人民共和国国家军用标准. 水面舰艇结构设计计算方法:GJB/Z 119-99[S]. 1999:23-25.
China State Shipbuilding Corporation.GJB/Z 119-99. Method for structural design and strength calculation of naval surface ships:GJB/Z 119-99[S]. 1999:23-25. |
 2016, Vol. 38
2016, Vol. 38
