2. 江苏现代造船技术有限公司, 江苏 镇江 212003
2. Jiangsu Modern Shipbuilding Technology Co. Ltd., Zhenjiang 212003, China
小水线面双体船是突破常规单体船以及双体船诸多性能限制的高性能船舶。当前对小水线面双体船耐波性能研究大多集中于直支柱布局的耐波性预报。但流体动力学的研究表明,斜支柱对船舶运动性能有很多有利影响。针对斜支柱小水线面双体船水动力性能研究,Peng Qian[1]运用 STF 法,通过比较直支柱、倾斜支柱和 NPL 双体船的频率响应曲线,证明支柱倾斜可提高小水线面双体船的耐波性能,并通过比较数值模拟和实验结果,证明该船波浪增阻较小,因为倾斜支柱可利用波浪能量,减小船在波浪中的能量消耗。Stefano Brizzolara等[2]通过对斜支柱小水线面双体船的阻力优化研究,证明了斜支柱较传统小水线面双体船的优越性。Latorre[3]运用 Hooft 法研究了斜支柱小水线面双体船的运动性能,通过与实验的比较,得出粘性阻尼对于预报垂荡、纵摇峰值时具有重要影响的结论。由此可知,对斜支柱小水线面双体船的水动力性能研究具有重要意义。根据船舶在波浪中的运动理论,本文对比不同支柱倾斜角度的小水线面双体船在波浪中的运动响应,以探究不同支柱倾斜角度对耐波性的影响。
1 基本理论小水线面双体船耐波性预报是通过求解运动方程,得到船舶各自由度运动幅值的频率响应函数,结合不规则波海浪谱,得到不同海况下船舶运动的统计特征值。但由于船体几何形状的特殊性,在求解运动方程中水动力系数时,与单体船存在 3 点不同[4]:1)片体间的流体动力干扰;2)粘性阻尼的影响;3)首尾鳍对水动力系数的贡献。本文基于三维势流理论,考虑了片体间的流体动力干扰,关于粘性阻尼的影响,采用添加临界阻尼矩阵[5]的方法。
1.1 基本方程及边界条件 基于理想流体的基本假设,假定流体为无粘、均匀、不可压缩有势的理想流体。用标量函数
| $ \frac{{{\partial ^2}\varPhi }}{{{\partial ^2}{x^2}}} + \frac{{{\partial ^2}\varPhi }}{{{\partial ^2}{y^2}}} + \frac{{{\partial ^2}\varPhi }}{{{\partial ^2}{z^2}}} = 0\text{,} $ | (1) |
同时,速度势满足相应的边界条件:
| $ \begin{array}{l} \displaystyle \frac{{{\partial ^{\rm{2}}}\varPhi }}{{\partial {{{t}}^2}}} \displaystyle + \frac{{g\partial \varPhi }}{{\partial y}} + \frac{1}{2}\nabla (\nabla \varPhi \cdot \nabla \varPhi ) + 2\nabla \varPhi \cdot \nabla \frac{{\partial \varPhi }}{{\partial t}} = 0\text{。} \end{array} $ | (2) |
1)自由面边界条件:
| $ \begin{array}{l} -{\omega ^2}{\phi _j} \!+\! 2{U_0}i\omega \displaystyle \frac{{\partial {\phi _{\rm{j}}}}}{{\partial x}} \!+ \!{U_0}^2\frac{{\partial {\phi _{^j}}^2}}{{\partial {x^2}}} \!+\! g\frac{{\partial {\phi _j}}}{{\partial z}} \!=\! 0,{{j = 1,2 \ldots ,7}}\text{;} \end{array} $ | (3) |
2)物面条件:
| $ \left. \begin{array}{l} \displaystyle-\frac{{\partial {\phi _j}}}{{\partial n}} = {n_j},j = 1,2...,6\\ \displaystyle \frac{{\partial {\phi _7}}}{{\partial n}} = \frac{{\partial {\phi _0}}}{{\partial n}} \end{array} \right\}\text{;} $ | (4) |
3)水底条件:
4)辐射条件:无穷远处有波浪向外传播
1.2 波浪谱本文选取的海浪谱为皮尔逊-莫斯科维奇(Pierson-Moskowitz)谱,该谱为第 11 届 ITTC 曾建议的暂定单参数标准波谱。P-M 谱的修正表达式如下:
| $ {{S}}(\omega ) = \frac{{{H_s}^2{T_z}}}{{8{\pi ^2}}}{(\frac{{\omega {T_z}}}{{2\pi }})^{-5}} {e^{\frac{{-1}}{\pi }{{(\frac{{\omega {T_z}}}{{2\pi }})}^{-4}}}}\text{。} $ | (5) |
其中Hs为有义波高,由波谱的零阶矩得到,即
根据谱密度的定义,输出的谱密度应为输入的谱密度乘以系统的频率响应函数模的平方
船舶运动响应方差:
| $ {\rm{E}} = \int_0^\infty {{{(\frac{{{\xi _k}}}{A})}^2}S(\omega ){\rm{d}}\omega } \begin{array}{*{20}{c}} {} \end{array} \text{。} $ | (6) |
式中:S(ω)为海浪谱表达式;
对小水线面双体船而言,由水的粘性引起的水动力阻尼和势流兴波阻尼相比,处于同一量级。若忽略粘性阻尼,会使得运动幅值的结果偏大,在峰值区将更加显著。由于三维势流理论无法计入粘性的影响,在水动力计算时,本文通过添加粘性阻尼矩阵来计及粘性影响。小水线面双体船又称为半潜式双体船,其结构形式和半潜式浮式结构相近。有关半潜式浮式结构的粘性阻尼的确定,文献[6]取临界阻尼的 10%,并通过实验研究验证了该方法的可行性。等效粘性阻尼由临界阻尼的比例求得[7],临界阻尼β0可由下式计算得到:
| $ {\beta _{\rm{0}}} = {\rm{2}}\sqrt {(M + {M_a}) \times {C_i}} \text{。} $ | (7) |
式中:M 为浮体的质量或惯性矩;Ma 为浮体附加质量;Ci 为静水回复力刚度。
按照式(6)求得横摇、纵摇、垂荡的临界阻尼[8],将临界阻尼的 10%加入阻尼矩阵中,计算其频率响应特性。
2 数值计算模型及参数设置 2.1 小水线面双体船主尺度本节主要讨论支柱倾斜角度对小水线面双体船在波浪中运动响应的影响,主尺度参数以直支柱为例。斜支柱小水线面双体船在母型船(直支柱 0°)的基础上倾斜 15°,30°,45°,通过微调吃水,保证排水量不变。母型船主尺度参数如表 1 所示。
|
|
表 1 船舶主尺度 Tab.1 Main particulars of the SWATH |
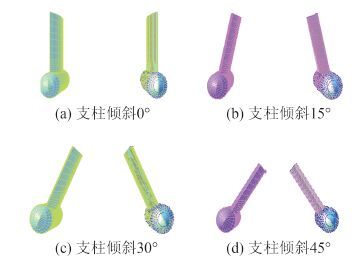
利用 SESAM/Genie 模块建立小水线面双体船的几何模型,如图 1 所示,分别为支柱倾斜 0°,15°,30°,45°的示意图。坐标系 x 轴指向船首为正,y 轴指向左舷为正,z 轴竖直向上为正,满足右手定则。
|
图 1 不同支柱倾斜角度的小水线面双体船 Fig. 1 Different inclined angle of SWATH vessels |
选取具有代表意义的 90°,135°,180°(横浪、首斜浪、迎浪等典型浪向角)共 3 个浪向;波浪频率设置:频率范围 0.2~1.5,步长为 0.05,共 27 个频率;3 个浪向和 27 个频率组合得到 81 个规则波。船体网格划分:纵向网格×周向网格(40×24),自由液面半径为 5 倍船长。设计航速为 15 kn,时间步长为 0.05 s。
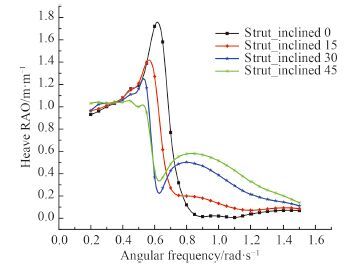
3 计算结果对比与分析借助 HydroD 软件的 Wasim 模块对不同方案的小水线面双体船进行耐波性分析,以纵摇、垂荡、横摇三自由度为研究重点,比较支柱倾斜对运动响应 RAO 的影响。由于计算工况较多,故仅列出具有代表意义的频率响应曲线,如图 2~图 4 所示,图中 0,15,30,45 表示不同支柱倾斜角度。
|
图 2 迎浪垂荡响应函数(180°) Fig. 2 Heave response function in head sea |
|
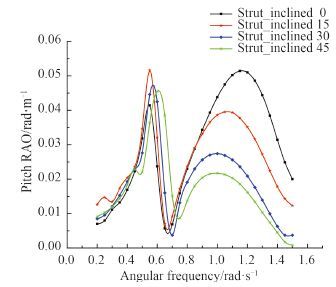
图 3 迎浪纵摇响应函数(180°) Fig. 3 Pitch response function in head sea |
|
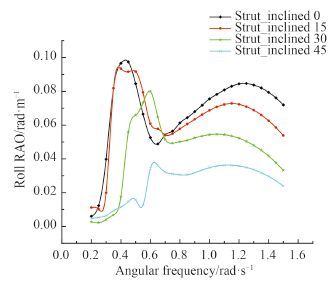
图 4 横浪横摇响应函数(90°) Fig. 4 Roll response function in beam sea |
根据图 2~图 4 可以得出:1)当波长λ趋于 0 m 时,船体运动响应很小;当波长趋于无限长时,船随着水质点一起运动,符合基本规律;2)对于垂荡而言,当 0.4 rad/s<ω<0.8 rad/s 时船体垂荡幅值较大,船舶处于共振区;随着支柱倾斜角度增加垂荡峰值逐渐减小,最小垂荡幅值为支柱倾斜角度为 45°时;3)对于纵摇而言,存在 2 个共振峰,第 1 个共振峰在 0.4 rad/s<ω<0.5 rad/s,第 2 个共振峰在 1 rad/s<ω<1.2 rad/s 时,2 个共振峰形成与 2 个片体的流体干扰有关;且随着支柱倾斜角度增加,第 2 个共振峰削弱明显;4)对于横摇,横摇峰值在 0.4 rad/s<ω<0.8 rad/s,且支柱倾斜对横摇有利。
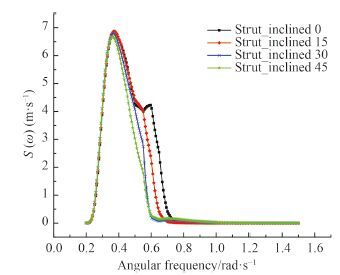
根据北大西洋和北太平洋每年海况统计资料[9],选取较为危险的 6 级海况(有义波高均值 5 m,模态周期 12.4 s)。由波浪谱与船舶响应函数(RAO)相结合,得到各自由度的运动响应谱,由运动谱的零阶矩得到运动有义值。不同支柱倾斜角度所对应的运动谱如图 5~图 7 所示,各自由度运动有义统计值见表 2。
|
|
表 2 典型浪向角下各自由度运动有义统计值 Tab.2 Significant statistics of different degree of freedom in typical wave direction |
|
图 5 迎浪垂荡响应谱(180°) Fig. 5 Heave response spectrum in head sea |
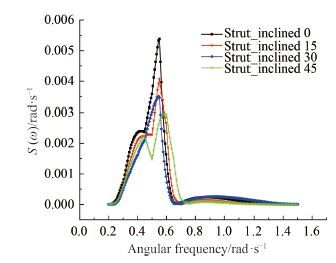
|
图 6 迎浪纵摇响应谱(180°) Fig. 6 Pitch response spectrum in head sea |
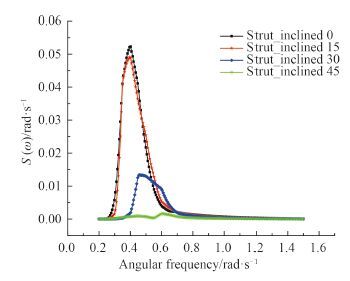
|
图 7 横浪横摇响应谱(90°) Fig. 7 Roll response spectrum in beam sea |
由表 2 的运动有义值可以得到:1)浪向角为 90°的横摇幅值最大,支柱倾斜角度对减小横摇响应明显。2)纵摇在迎浪(180°)时的响应最大;随着支柱倾斜角度的增加,纵摇幅值逐渐减小。3)浪向对垂荡响应并不十分敏感,横浪、首斜浪、迎浪下的垂荡有义值相差不大。4)在设计航速下,6 级海况中 4 种支柱倾斜角度的小水线面双体船的纵摇响应较小;支柱倾斜对改善横摇响应具有较大作用;垂荡有义响应幅值较大,需采取相应措施予以改善。
4 结语本文研究了不同支柱倾斜角度的小水线面双体船的耐波性。比较横摇、纵摇、垂荡的频率响应函数和运动有义幅值,观察得到随着支柱倾斜角度的增加,小水线面双体船在波浪中的运动峰值逐渐减小的规律。其流体动力机理是支柱的倾斜增加了船的附加质量和阻尼,从而使频率响应函数的峰值减小。同时研究证明小水线面双体船具有优良的耐波性能,通过倾斜支柱可进一步提高耐波性能,能满足更高海况下船舶运营作业的需求。
| [1] | QIAN P, YI H, LI Y H. Numerical and experimental studies on hydrodynamic performance of a small-waterplane-area-twin-hull (SWATH) vehicle with inclined struts[J]. Ocean Engineering , 2015, 96 :181–191. DOI:10.1016/j.oceaneng.2014.12.039 |
| [2] | BRIZZOLARA S, CURTIN T, BOVIO M, et al. Concept design and hydrodynamic optimization of an innovative SWATH USV by CFD methods[J]. Ocean Dynamics , 2012, 62 (2) :227–237. DOI:10.1007/s10236-011-0471-y |
| [3] | LATORRE R, VASCONSELLOS J. Study of hull angle influence on SWATH heave and pitch motions[J]. Naval Engineers Journal , 2001, 113 (1) :63–70. DOI:10.1111/nej.2001.113.issue-1 |
| [4] |
黄鼎良.
小水线面双体船性能原理[M]. 北京: 国防工业出版社, 1993 : 110 .
HUANG Ding-liang. SWATH performance principle[M]. Beijing: National Defense Industry Press, 1993 : 110 . |
| [5] | Sesam HydroD User Tutorial. Global response of a damaged semi-submersible offshore platform in Frequency domain by Wasim and Wadam |
| [6] | RODDIER D, PEIFFER A, AUBAULT A, et al. A generic 5 MW WINDFLOAT for numerical tool validation & comparison against a generic spar[C]//Proceedings of the ASME 201130th International Conference on Ocean, Offshore and Arctic Engineering. Rotterdam:ASME, 2011:2011-50278 |
| [7] |
冯炎鑫. 三体船在波浪上的运动响应计算[D]. 天津:天津大学, 2013.
FENG Yan-xin. Motion response calculation of trimaran in wave[D]. Tianjin:Tianjin University, 2013. |
| [8] |
王涵. 小水深半潜型风电浮式基础的耦合动力分析与试验研究[D]. 天津:天津大学, 2013:26-28.
WANG Han. Coupling dynamic analysis and experimental research of semi-submersible floating foundation for wind power in the shallow water[D]. Tianjin:Tianjin University, 2013:26-28. |
| [9] | FALTINSEN O M. 船舶与海洋工程环境载荷[M]. 杨建民, 肖龙飞, 葛春花, 译. 上海:上海交通大学出版社, 2008:24-25. |
 2016, Vol. 38
2016, Vol. 38
