陆基条件下的自动舵性能检测平台对于自动舵的研发调试及检修具有非常重要的意义[1]。船舶运动模型作为该平台的基础与核心,对于其适用性的研究必不可少。描述舰船操纵性的运动模型主要分为 3 类[2]:1)以 Abkowitz 为代表的整体型结构模型;2)日本拖拽水池委员会提出的分离型结构模型;3)20 世纪 50 年代末野本谦作提出的响应性模型。
响应型船舶运动模型是从控制工程的观点将船舶看成一个动态系统而提出的。以舵角为系统输入,首摇角速度为系统输出。使用分离型模型对船舶运动进行建模和仿真,需要大量详尽的船型(包括舵和桨)数据和繁杂的计算,而整体性模型同样需要进行全面的船模试验以测定流体动力导数。相比于分离型模型或整体型模型,响应型船舶运动模型除了形式简洁,便于使用,其参数可直接从实船试验获得而无需模型试验,自动消除了尺度效应,在船舶操纵性研究以及航迹自动控制研究方面都得到广泛应用。
现有的航向航迹自动舵检测平台使用的一阶线性 KT 方程,由于其忽略了回转过程纵向速度的变化以及横向速度与首摇角之间的耦合等,在对于大舵角操舵运动仿真以及高速船的运动仿真时误差较大,在实际使用中具有一定的局限性。国际电工委员会制定的航迹系统性能标准(IEC62065)中提出了包括纵向速度及横向速度的船舶三自由度运动模型,本文利用该模型对不同船型在不同条件下的操舵运动进行仿真试验,并且与现有的一阶线性 KT 方程及加入非线性项的一阶 KT 方程的仿真结果作比较分析,讨论船舶回转运动中横向速度对于首摇运动的耦合作用,KT 方程的非线性项对运动模型输出的首摇角误差大小的影响。
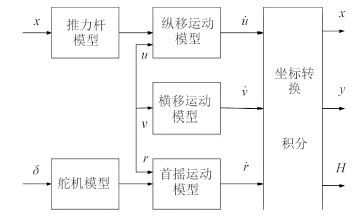
1 IEC62065 运动模型的建立及仿真试验国际电工委员会制定的航迹系统性能标准(IEC62065)中[3]提出了包括纵向速度及横向速度的船舶三自由度运动模型,它是以指令舵角和指令推力杆位置作为系统的输入,以首摇角速度纵向速度以及横向速度等运动参数作为系统输出,将这些速度参数经过积分及坐标变换等一系列计算可以得到船舶的航向角、坐标和轨迹等运动参数。模型的主要组成部分为推力杆响应模型、舵机响应模型、纵移响应模型、横移响应模型及首摇响应模型等 5 个基本模块。原理如图 1 所示。
|
图 1 船舶运动模型原理框图 |
IEC62065 中提出的船舶运动模型将复杂的螺旋桨推进力模型简化为线性的推进装置响应方程,并进行归一化处理,经处理后的响应模型如下:
| $ \dot X{'} = \left\{ {\begin{aligned} & {2/{T_P},X{'} < {P_d}{'}}\text{,}\\ & {0,X{'} = {P_d}{'}}\text{,}\\ & {-2/{T_P},X{'} > {P_d}{'}}\text{。} \end{aligned}} \right. $ | (1) |
式中:X' 为归一化的推力杆位置,取值为-1 ~ 1; Pd' 为归一化的推力杆指令;TP为推进装置时间常数,和推力装置的响应速率有关。
舵机的响应特性采用简化的线性方程表达,模型如下:
| $ {\dot \delta _a} = \left\{ {\begin{aligned} & {2{\delta _{\max }}/{T_\delta },{\delta _a} < {\delta _d} + \Delta }\text{,}\\ & {0,{\delta _a} = {\delta _d} + \Delta }\text{,}\\ & {-2{\delta _{\max }}/{T_\delta },{\delta _a} > {\delta _d} + \Delta }\text{。} \end{aligned}} \right. $ | (2) |
式中:δa 为实际舵角;δmax 为最大舵角;δd 为指令舵角;Δ 为舵角偏差;Tδ 为舵机的响应时间常数,即舵机从左满舵到右满舵所经历的时间。
1.2 船舶运动方程船舶沿附体坐标系的 x 轴方向,即船首方向的运动称为船舶的纵移运动。纵向运动速度的微分方程为:
| $ {M_u}\dot u = X + {M_u}vr-{R_u}u\text{。} $ | (3) |
式中,Mu 为船舶的质量和 x 轴方向上附加质量总和;u,v,r 分别为船的纵移速度、横移速度以及首摇角速度;X 为推进力;Ru 为 x 轴方向上的阻力系数。
对于 Ru ,当船舶以最大速度运动时,有 Ru = Xmax/umax 。令 τu = Mu / Ru ,代入上式可得:
| $ {\tau _u}\dot u + u = {u_{\max }}X{'} + {\tau _u}vr\text{,} $ | (4) |
船舶沿附体坐标系的 y 轴方向的运动称为船舶的横移运动。横向速度的微分表达式如下:
| $ {M_v}\dot v = {M_v}ur-{R_v}v\text{。} $ | (5) |
式中:Mv 为船舶质量和 y 轴方向上附加质量总和;Rv 为 y 轴方向上的阻力系数。令 τv = Mv/Rv ,代入上式可得:
| $ {\tau _v}\dot v + v = {\tau _v}ur\text{。} $ | (6) |
船舶的首摇运动即船舶绕附体坐标系中的 z 轴所做的旋转运动。在静水条件下,首摇角速度的微分表达式为:
| $ {I_z}\dot r = {K_r}\frac{{{u_{\max }}X{'}}}{L}{\delta _a} + \gamma L{R_v}(v-\gamma Lr)-{R_r}r\text{。} $ | (7) |
首摇运动方程的等式右边包含了 3 个方面的力矩作用,即水流的阻力矩 Rγr ,横移速度造成的力矩 γLRv ( v-γLr )和舵提供的转向力矩
| $ \dot r = {K_r}{'}{\delta _a}{K_u}X{'}{\tau _u}/L{\delta _{\max }} + 12\gamma (v-\gamma Lr)/L{\tau _v}-r/{\tau _r}\text{。} $ | (8) |
根据上述运动方程,可通过坐标变换求出船舶相对于固定坐标系的速度,进而求得船舶运动的轨迹方程。
| $ \left[{\begin{array}{*{20}{c}} {\dot x}\\ {\dot y}\\ {\dot \psi } \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\cos \psi } & {-\sin \psi } & 0\\ {\sin \psi } & {\cos \psi } & 0\\ 0 & 0 & 1 \end{array}} \right]\left[{\begin{array}{*{20}{c}} u\\ v\\ r \end{array}} \right]\text{。} $ | (9) |
一阶线性 KT 方程根据 MMG 模型,由船舶运动特点简化成线性船舶运动数学模型[3]。当附体坐标系原点与船舶重心重合时,MMG 模型可归结为下式:
| $ \left\{ \begin{aligned} & (m + {m_x})\dot u-(m + {m_y})vr = {X_H} + {X_P} + {X_R}\text{,}\\ & (m + {m_y})\dot v + (m + {m_x})ur = {Y_H} + {Y_P} + {Y_R}\text{,}\\ & ({I_{zz}} + {J_{zz}})\dot r = {N_H} + {N_P} + {N_R}\text{。} \end{aligned} \right. $ | (10) |
式中: mx,my,Jxx,Jzz 分别为附加质量与附加惯性矩; FHFPFR 分别为各自由度上流体粘性力、推进力和舵力。
将作用于船体、桨和舵上的流体动力,螺旋桨推力及舵力进行泰勒级数展开,略去 2 阶及以上高阶小量,只保留 1 阶项,并且忽略纵向运动速度的变化,将纵向运动的表达式与横向运动,首摇运动的表达式解耦,经整理可将上面的 MMG 模型可简化为下式:
| $ \left. {\begin{aligned} {(m + {m_y})\dot v = {Y_v}v + ({Y_r}-(m + {m_x}){u_0})r + {Y_\delta }\delta }& \\ {({I_{zz}} + {J_{zz}})\dot r = {N_v}v + {N_r}r + {N_\delta }\delta }& \end{aligned}}\,\,\right\}\text{。} $ | (11) |
将上述方程进行拉普拉斯变化并求解即可得到舵角到首摇角速度的传递函数:
| $ H(s) = \frac{{r(s)}}{{\delta (s)}} = \frac{{K(1 + {T_3}s)}}{{(1 + {T_1}s)(1 + {T_2}s)}}\text{,} $ | (12) |
经泰勒公式展开并化简,令 T = T 1 + T 2-T 3 ,忽略高阶小量,可以将传递函数降为一阶,即
| $ H(s) = \frac{{r(s)}}{{\delta (s)}} = \frac{K}{{Ts + 1}}\text{,} $ | (13) |
进一步可计算船舶的运动轨迹坐标:
| $ \left. {\begin{array}{*{20}{c}} {x(t) = x(0) + \int_0^t {u\cos \psi (t){\rm d}t} }\\ [5pt] {y(t) = y(0) + \int_0^t {u\sin \psi (t){\rm d}t} } \end{array}} \right\}\text{。} $ | (14) |
本文使用 Simulink 对 IEC62065 标准中的给出的 2 种船型分别进行操舵运动仿真[4],使用 Matlab 软件的系统识别工具箱计算出与原模型拟合程度最高的 K 和 T 参数,比较分析一阶线性 KT 模型在不同船型,不同操舵运动下的误差,讨论一阶线性 KT 方程的应用的局限性。
2种船型的模型参数如表 1 所示。
|
|
表 1 船型参数 Tab.1 The parameters of ships |
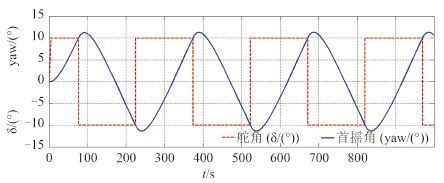
对于 B 型集装箱船,首摇稳定系数为 0,即横移阻力对船舶的作用点与船舶重心基本重合,不会产生绕 Z 轴的力矩从而影响船舶的首摇运动。故 B 型集装箱船的首摇运动响应模型可直接简化为以舵角作为系统输入,首摇角作为系统输出的一阶线性响应方程,其 K 和 T 参数可直接由原模型计算得到。对 B 型船进行阶跃操舵运动的仿真试验,并使用 Matlab 进行系统辨识得到 K = 0.02,T = 23,2 种模型首摇角输出曲线可完全拟合。对 B 型船进行 Z 型操舵运动仿真试验,得到的输入舵角和输出首摇角的时间历史曲线如图 2 所示。
|
图 2 B 型船的 Z 型运动仿真试验 |
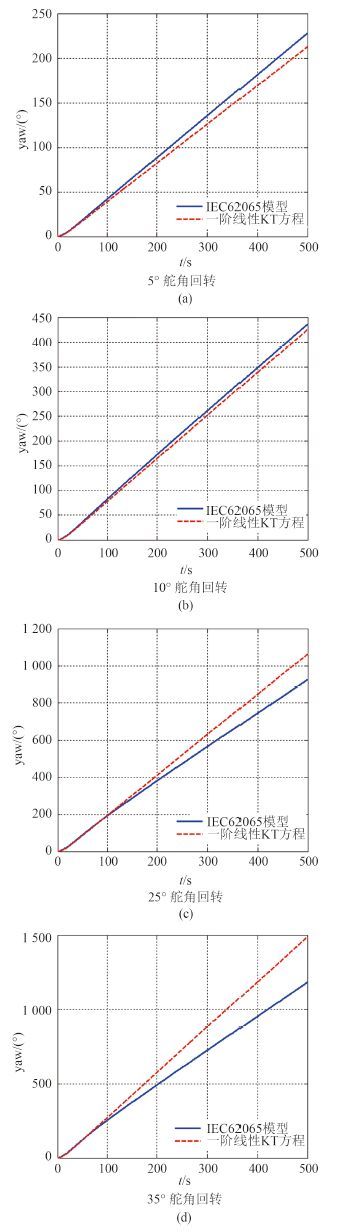
对于 A 型渡轮,首摇角稳定系数不为 0,即横移阻力对船舶的作用点与船舶重心稍有偏移,从而影响了船舶的首摇运动,原模型的首摇方程不能直接化为一阶线性响应模型的形式。对 A 型渡轮进行 10° 舵角的阶跃操舵运动仿真试验,将舵角作为输入,艏摇角作为输出,对系统进行参数辨识,得到 K = 0.08,T = 10.8。分别对原模型和一阶线性 KT 方程进行不同舵角下的回转试验。图 3 所示为在不同舵角(5°,10°,25°,35°)下分别用 2 种模型仿真得到的首摇角时间历史曲线。
|
图 3 不同舵角下首摇角时间历史曲线 |
在 500 s 以内,不同舵角下一阶线性 KT 方程输出首摇角的最大误差如表 2 所示。
|
|
表 2 A 型船在不同舵角下的输出首摇角误差 Tab.2 The error of yawing angle of ship A under different rudder angles |
可以看出,简化一阶线性 KT 模型只在 10° 舵角附近与原模型拟合度较高,10° 时输出首摇角的误差百分比最大为 2.3%,而在其他舵角下的误差较大,相似度较低。在 35° 舵角下 2 模型的输出首摇角的误差百分比达到 25.9%。由于横移阻力对首摇力矩的影响,K 和 T 的值较明显地依赖于输入舵角的变化。因此对于 A 型渡轮,一阶线性 KT 方程不适用。此时需引入非线性项 ar 3,其中 a 为新引入的常数,r 为首摇角速度。加入非线性项的一阶 KT 方程形式如下:
| $ T\dot r + r + a{r^3} = K\delta \text{,} $ | (15) |
船舶在定常回转时,
| $ r + a{r^3} = K\delta \text{。} $ | (16) |
对 A 型渡轮进行一系列给定舵角下的定常回转运动试验,得到在不同舵角下的定常回转运动状态时的稳定艏摇角速度如表 3 所示。
|
|
表 3 定常回转状态下的首摇角速度 Tab.3 The angular velocity of yawing angle during constant turning |
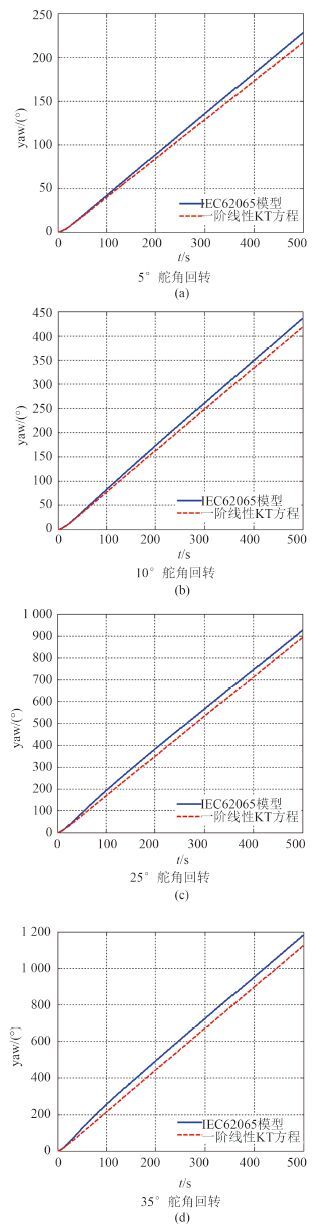
应用最小二乘法对上表中的数据进行拟合,取 a = 0.073,K = 0.09。分别对原模型和加入非线性项的一阶 KT 方程进行不同舵角下的回转试验。如图 3(c)所示,是在不同舵角(5°,10°,25°,35°)下分别用 2 种模型仿真得到的首摇角时间历史曲线。
在 500 s 以内,不同舵角下非线性的一阶 KT 方程输出艏摇角的最大误差如表 4 所示。
|
图 4 不同舵角下艏摇角时间历史曲线 |
|
|
表 4 B 型船在不同舵角下的输出首向角误差 Tab.4 The error of yawing of ship B under different rudder angles |
比较上述 2 次试验的图形和数据。相较于一阶线性 KT 方程,加入非线性项的一阶 KT 方程得到的首摇角时间曲线和使用 IEC62065 提供模型得到的首摇角时间曲线的拟合度明显提高。上述试验中,舵角为 35° 时,2 种模型仿真得到的首摇角的最大误差为 4.7%,在 5% 的范围内,可以认为 2 种模型具有较好的相似度。
4 结语本文对国际电工委员会制定的航迹自动舵标准(IEC62065)中提供的船舶运动模型进行仿真试验,并与一阶线性 KT 方程的仿真结果进行比较,介绍了加入非线性项的一阶 KT 方程,探讨了非线性项对不同船型在不同舵角操舵运动状态下的影响。得出结论如下:
1)对于上述仿真实验中 B 型船这样的中速集装箱船,其受力特点是横向力作用点与船舶重心基本重合,故可以忽略横向速度对转首力矩的影响,进而两模型可以等价转换。然而对于 A 型船这样的小型高速渡轮,横向力对转首力矩的影响较大,首摇角速度与横向速度之间的耦合不可以忽略,故两运动模型输出首摇角的误差随输入舵角的变化而产生的变化较大,在 35° 舵角下,500 s 内,输出首摇角的最大误差达到 25.9%。
2)加入非线性项的一阶 KT 方程能够较好地对线性 KT 方程进行修正。在小舵角范围内误差和线性 KT 方程相近,而在 35° 舵角下,500 s 内,输出首摇角的最大误差缩小至 4.7%,可以认为与 IEC62065 提供的运动模型有较好的相似度。对于航迹航向舵自动检测平台而言,非线性的一阶 KT 方程考虑到了船舶运动方程中的非线性项,能够更好地模拟船舶的真实运动状态,同时减少了计算量,使用较为方便。
船舶的运动特性从本质上来看是非线性的,而使用一阶线性 KT 方程是建立在忽略流体动力的非线性特性以及纵向速度变化的基础之上。实验表明,对于部分船型,忽略流体动力的非线性特性会带来较大的误差。另一方面,对于高速船,回转时会产生较大的横倾,这时横倾会对首摇运动产生较大影响,这时需要考虑二者之间的耦合。关于高速船回转时横倾角的影响有待进一步的研究。
| [1] |
陈永冰, 周岗, 李文魁. 舰船航迹控制系统运行检测平台的设计与实现[J]. 海军工程大学学报 , 2011, 23 (4) :38–42.
CHEN Yong-bing, ZHOU Gang, LI Wen-kui. Design and implement of operation and detection platform for ship track control system[J]. Journal of Naval University of Engineering , 2011, 23 (4) :38–42. |
| [2] | 贾欣乐, 杨盐生. 舰船运动数学模型[M]. 大连: 大连海事大学出版社, 1999 : 1 -2. |
| [3] | IEC. Maritime navigation and radiocommunication equipment and systems-track control systems-operational and performance requirements, methods of testing and required test results:IEC62065-2014[S].[S.l.]:IEC, 2014. |
| [4] |
岳晋, 任光, 曹辉. 基于Simulink的船舶运动模型动态仿真研究[J]. 大连海事大学学报 , 2009, 35 (4) :13–16.
YUE Jin, REN Guang, CAO Hui. Dynamic simulation of ship motion model based on Simulink[J]. Journal of Dalian Maritime University , 2009, 35 (4) :13–16. |
| [5] | GROSENBAUGH M A. Transient behavior of towed cable systems during ship turning maneuvers[J]. Ocean Engineering , 2007, 34 (11/12) :1532–1542. |
| [6] | PéREZ F L, CLEMENTE J A. The influence of some ship parameters on manoeuvrability studied at the design stage[J]. Ocean Engineering , 2007, 34 (3/4) :518–525. |
| [7] |
陈宁, 龚苏斌. 船舶回转运动仿真[J]. 舰船科学技术 , 2013, 35 (3) :9–14.
CHEN Ning, GONG Su-bin. The research on the ship turning movement based on Simulink[J]. Ship Science and Technology , 2013, 35 (3) :9–14. |
| [8] | TZENG C Y, CHEN J F. Fundamental properties of linear ship steering dynamic models[J]. Journal of Marine Science and Technology , 1999, 7 (2) :79–88. |
| [9] | ABKOWITZ M A. Measurement of hydrodynamic characteristics from ship maneuvering trials by system identification[J]. SNAME Transaction , 1980, 33 (88) :283–318. |
| [10] |
孙才勤, 王心红, 许建, 等. 船舶自动舵仿真模拟器的研制[J]. 大连海事大学学报 , 2014, 40 (1) :1–4.
SUN Cai-qin, WANG Xin-hong, XU Jian, et al. Research of simulator for automatic hydraulic steering gear[J]. Journal of Dalian Maritime University , 2014, 40 (1) :1–4. |
 2016, Vol. 38
2016, Vol. 38
