2. 高新船舶与深海开发装备协同创新中心(船海协创中心), 上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China
随着水面舰艇和潜艇航速的提升,水弹性振动对船体强度以及疲劳寿命产生的影响已引起了造船界的广泛关注。舰艇附件和海洋结构部件在粘性流体中运动时,引起流动分离,生成旋涡,造成涡激振动,可能导致结构破坏。利用水弹性的研究结果,分析粘性流体通过翼型振荡物的振动研究,国内外的研究并不多。现有文献结果大多是假定圆柱、机翼静止不动的情况下进行的。多数情况下水翼不是完全固定不动的,而是在弹性轴处受到非线性约束,水翼在流体的作用下会产生涡的脱落等复杂现象,由此流体力作用于结构物本身产生耦合效应涡激振动。如水翼艇中的水翼,潜艇中的舵翼等船舶构件作为动力学系统,设计不当时,在流场中高速运动时将会产生有害的涡激颤振,导致结构破坏。
流固耦合研究早期集中在气动弹性力学,发展至今已经有较为成熟的理论体系,其大部分理论结果都可直接应用于水弹性力学中。早在 20 世纪 30 年代 Theodorsen[1]提出基于非定常气动力线性化精确解的不可压缩、无粘流的 Theodorsen 非定常气动力模型,该模型同样可以处理二维水翼的非定常力。Huang等[2]对 NACA0012 翼型进行实验分析,并探讨了翼根连接处与翼梢对涡激振动的影响。Jung[3]通过实验对低雷诺数下机翼绕流形成的涡街,发现机翼振动情况下的涡脱频率相对于机翼静止不动时要小。王囡囡[4]采用片条理论的简化非定常气动力方法研究机翼气动弹性系统的动态特性,提出了一种基于实测柔度的颤振主动控制方法。另一方面至 20 世纪 70 年代后期,船舶水弹性力学理论和分析方法取得了显著的进展,并广泛应用到船舶与海洋工程领域的流固耦合分析中。早期的工作主要集中在试验研究,Davidson 实验室对水翼做了大量的试验研究,主要集中在以 2 个自由度理想翼型为出发点,观察测量水翼在水洞试验中的振动、空泡、压力分布等。Henry[5] 进行了一系列的模型试验,对水翼各参数以及临界颤振速度的影响作了理论上探讨。余志兴[6-7]运用 N-S 方程数值模拟了粘性流场中二维机翼的水弹性振动,在此基础上,刘晓宙[8]利用有均流时二维运动物体的声辐射方程,研究了大攻角下二维水翼的声辐射,结果表明:涡脱频率和机翼的固有振动频率一致时,声辐射达到最大。Chae[9-10]对2个自由度下的二维水翼进行了一系列系统的研究,探讨了附加水质量、水动力阻尼、非线性流固耦合响应等对水翼稳定性的影响。
本文建立了 2 个自由度下二元水翼的流固耦合模型,分别利用大涡模拟方法和龙格库塔法求解流体结构方程,界面数据传递通过自编函数实现。对 NACA0012 翼型在不同工况下的绕流振动进行分析,并分别在时域和频域上对振动情况进行分析。
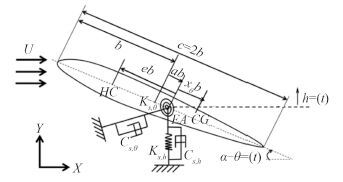
1 数学模型 1.1 刚体模型本文将探讨悬臂式、二维翼型在不可压缩流体中的动态响应与稳定边界,假定水翼仅在翼展方向存在 2 个自由度运动,即对应船舶六自由度中的垂荡与纵摇,如图 1 所示。
|
图 1 两自由度水翼模型 Fig. 1 Two degrees of freedom hydrofoil models |
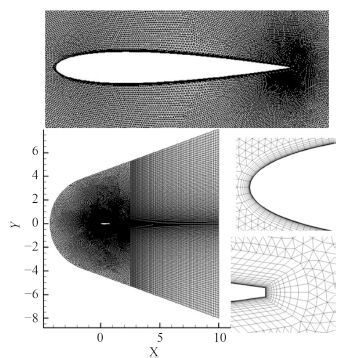
|
图 2 水翼计算网格 Fig. 2 Grid of hydrofoil |
其中,水翼弦长 c = 2b,来流速度为 U,初始攻角为 α。EA 为水翼弹性中心(也即是二维翼型刚心),位于翼弦中点后 ab 处,a 为弹性中心到翼弦中点距离的无量纲量,b 为半弦长。翼型在弹性轴处由一个线弹簧和一个扭转弹簧支撑在弹性轴处,垂直方向位移与旋转均是在弹性轴上测量,h(t) 向上为正,θ(t) 逆时针为正,分别称为水翼的垂荡运动和纵摇运动。HC 为水动力中心,位于弹性中心前缘 eb 处,即是流体作用力合力的作用点。重心 CG 位于弹性中心后缘 xθb 处,xθ 为重心到弹性中心距离的无量纲量。
两自由度水翼无量纲运动方程为:
| $ \left[\!\!\! {\begin{array}{*{20}{c}} m\!\! & \!\!{{S_\theta }}\!\!\\ {{S_\theta }} \!\! & \!\! {{I_\theta }}\!\! \end{array}} \!\!\!\right]\left\{ {\begin{array}{*{20}{c}} \!\!{\ddot h}\!\! \\ \!\!{\ddot \theta }\!\! \end{array}} \right\} \!+\!\left[\!\!\! {\begin{array}{*{20}{c}} {{C_h}}\!\! & \!\!0 \\ 0\!\! & \!\!{{C_\theta }} \end{array}}\!\! \right]\left\{ {\begin{array}{*{20}{c}} \!\!{\dot h}\!\!\\ \!\!{\dot \theta }\!\! \end{array}} \right\} \!+ \!\left[\!\!{\begin{array}{*{20}{c}} {{K_h}}\!\! & \!\!0 \\ 0 \!\!& \!\!{{K_\theta }} \end{array}}\!\! \right]\left\{ {\begin{array}{*{20}{c}} \!\!h\!\!\\ \!\!\theta\!\! \end{array}}\! \right\}\!\! =\!\! \left\{\!\!\! {\begin{array}{*{20}{c}} L\\ M \end{array}}\!\!\! \right\}\text{。} $ | (1) |
式中:
上述方程组可简化为:
| $ {{ M}_s} \ddot{ X} + {{ C}_s}\dot { X} + {{ K}_s}{ X} = { F}\text{。} $ | (2) |
式中:Ms,Cs,Ks 分别为水翼惯性、阻尼和刚度矩阵;F 为流场力矩阵;X 为两自由度上广义位移矩阵。
1.2 流体模型如图 1 所示,流场分为 3 个区域:水翼近场加密网格为动区域;远场采用非结构网格为变形区域;延长水翼后方网格以观察尾流。
基于商业软件 Fluent 有限体积法对二维水翼进行瞬态绕流分析,利用 UDF 控制刚体与网格的运动。大涡模拟相较于平均雷诺数法可以提供丰富的大涡旋信息,且能计算出壁面处的压强脉动。本文在对 Fluent 中几种经典湍流模型进行计算比较后选用 LES 作为后续的计算模型。
流场的连续性方程和不可压缩 N-S 方程可以写为:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}(\rho {\bar u_i}) = 0\text{,} $ | (3) |
| $ \frac{\partial }{{\partial {x_i}}}(\rho {\bar u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {\bar u_i}{\bar u_j}) = \frac{\partial }{{\partial {x_i}}}(\mu \frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}})-\frac{{\partial \bar p}}{{\partial {x_i}}}-\frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}\text{。} $ | (4) |
亚格子应力
| $ {\tau _{ij}}-\frac{1}{3}{\tau _{kk}}{\delta _{ij}} =-2{\mu _t}{\bar S_{ij}}\text{。} $ | (5) |
对于 Smagorinsky-Lilly 模型
| $ {\mu _t} = \rho L_s^2\left| {\bar S} \right|\text{。} $ | (6) |
式中:
建立 CFD 模型和计算结构动力学模型后,需要建立有效的界面耦合程序来联系这 2 个单独的计算模型。耦合界面不匹配网格间信息的准确交换,直接影响耦合计算精度,是获得真实物理解的关键环节之一。
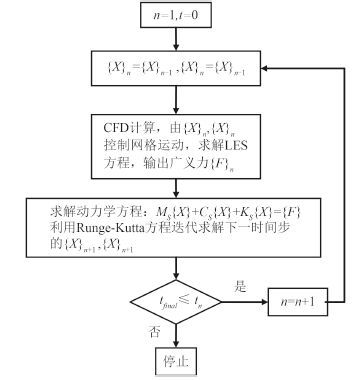
二维水翼的耦合方式如图 3 所示。初始条件
|
图 3 .耦合算法流程图 Fig. 3 Coupled algorithm flowsheet |
水翼结构参数取值如下:总弦长 c=1 m,垂荡、纵摇固有频率
对 1 m/s 来流下涡激振动采用大涡模拟数值分析,刚心位置取在水翼前缘。图中流场参数为 Re=106。
从图 4 可看出,10° 攻角下水翼后缘涡街脱落较为明显,在水翼前缘和尾翼处均有涡的形成,以平行于来流的方向向尾部脱离,并在尾流中形成涡街。而 0°攻角下由于水翼振幅很小,仅在尾翼处有涡的形成,且很快消散。目前关于翼型绕流的涡激振动研究,为了获得翼型绕流周期性的涡发放,大多集中在大攻角工况下。本文以 10°攻角作为主要分析对象,发现大涡模拟能够较好的捕捉复杂湍流中的细节,而在一般 k-ω等雷诺平均模型中,小攻角水翼绕流无法捕捉到尾部涡这一特征。

|
图 4 NACA0012 水翼压力、流场以及涡量云图,Re=106 Fig. 4 Pressure,velocity and vorticity contours of hydrofoil Re=106 |
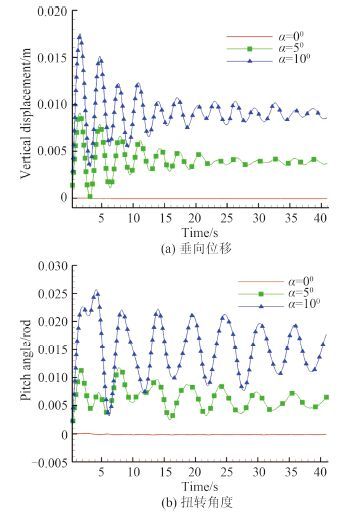
|
图 5 不同攻角下振动情况对比 U=1 m/s Fig. 5 Hydrofoil vibration under different attack angle |
保持其他参数不变,改变初始攻角对比其对水翼绕流振动的影响,垂荡运动和纵摇运动结果如图 6 所示。
|
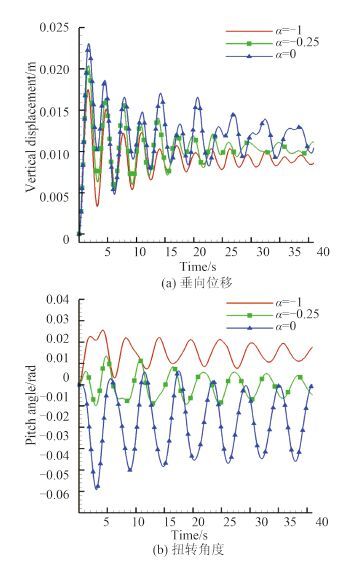
图 6 刚心位置对振动情况的影响 U=1 m/s,α=10° Fig. 6 Hydrofoil vibration under different stiffness center |
显而易见,攻角越大,其升力与力矩就越大,相应 2 个自由度上的位移就越大。从图中可看到,不同攻角下的振荡平衡位置随攻角增大而增大。在 0° 攻角下,仅在水翼尾部形成较小的涡,且很快耗散掉,图 5 中可以看出,0° 攻角下,水翼振荡位移的幅值非常小,且频率较高,没有体现出一定的周期性。本文尝试将 0° 攻角来流速度提升至 4 m/s,2 个自由度上的位移仍保持非常小,且周期性较为紊乱。初步得出结论:0° 攻角在没有初始扰动的情况下很难产生大幅振动的情况,攻角越大,振动平衡位置越偏离初始位置。且垂荡运动幅值衰减较明显,纵摇运动幅值衰减较慢。
根据气动弹性力学理论,重心位于刚心线之前就不会发生颤振,飞行器机翼设计时多采用在翼面前缘防止配重,使重心前移的方式来避免颤振。当重心位置一定时,应使刚心靠后一些(与重心靠近),以此来提高颤振速度。对于水翼而言,刚心位置同样对颤振临界条件有着至关重要的作用。通过升力力矩公式可以看出,绕弹性轴力矩的大小与刚心位置有关,刚心位置的改变直接影响到力矩的大小,进而影响到纵摇运动,由于流体-结构的耦合作用,结构运动状态的改变将导致流场变化从而导致垂荡运动的变化。图 6 显示 2 个自由度上位移都出现了一定幅度的衰减,且刚心位置对纵摇振动平衡位置的影响较垂荡运动更加明显。
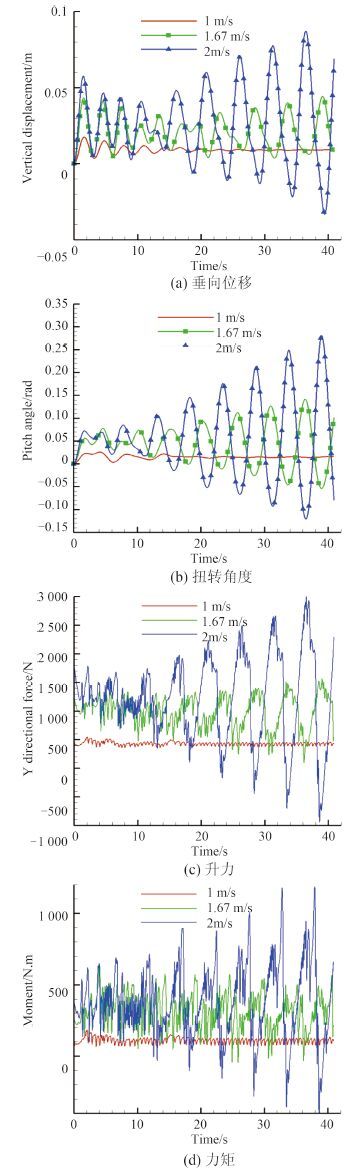
从图 7 可见,随着来流速度增大,水翼在 2 个自由度上振动不断加剧,可以看到 1.67 m/s 工况下纵摇自由度振幅随着时间不断增大,而垂荡自由度的振幅经过小幅度减小后又继续增大直到相对保持平稳。初步判定,本文所采用水翼的颤振临界速度在 1.67 m/s 附近。其中,1 m/s 时,升力和力矩在数值上保持微小的波动,可近似看作是固定力作用在水翼上,由于运动过程中的阻尼作用,振动幅度随时间逐渐衰减。而 2 m/s 时,升力和刚心处力矩幅度随时间不断增大,从而导致 2 个自由度上的位移也不断增大,且此时水翼纵摇自由度瞬时水动力与弹性位移之间有约 180°的位相差,水翼已经进入颤振状态,振动幅度不断扩大从而导致结构的破坏。为了更直观地观察水翼颤振情况,做出以上 3 组速度下的相图和对应
|
图 7 不同来流速度下振动情况对比,α=10°,a = -1 Fig. 7 Hydrofoil vibration under different velocity |

|
图 8 不同来流速度下纵摇运动相图及频谱 Fig. 8 Motion phase diagram and velocity spectrum in various velocity |
来流速度较小时,流体对水翼做负功,水动力对水翼运动起阻尼作用,振动逐渐衰减最终稳定于某一平衡位置。速度为 1 m/s 时,由相图分析看出系统未出现极限环运动,2 个自由度上的振幅不断减小。由频谱图可知,垂荡和纵摇自由度均由 2 个频率成分叠加而成,其中垂荡自由度主要频率成分为 0.35 Hz、纵摇自由度主要频率成分为 0.18 Hz 和 0.35 Hz。来流速度为 1.67 m/s 时,此时垂荡自由度含有 2 个频率分别为 0.195 Hz 和 0.34 Hz。纵摇自由度的主要频率为 0.195 Hz,由图 8 可知,此速度下纵摇方向已不稳定,说明频率较小的成分起到主要作用时系统会发生不稳定现象。速度为 2 m/s 时,2 个自由度上的主要频率成分均为 0.195 Hz,与 1.67 m/s 纵摇不稳定时的频率相同,次要频率成分为 0.3 Hz 且幅值远小于 0.195 Hz,此时系统发生颤振,也同样印证了上述说法,即较小频率成分起主要作用时系统不稳定。表明来流速度增大至越过临界速度后,水动力做正功,水翼发生自激振动,振幅不断增大而导致振动发散,颤振是指结构物具有 2 个自由度以上的以同一频率耦合起来的振动现象[11]。由频谱图可以看出,随速度增大,2 个自由度上的主要频率成分趋于一致,且低频成分逐渐起到主导作用,另一个频率成分的影响逐渐降低。
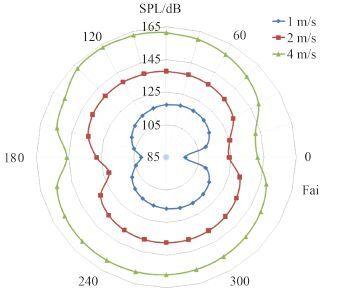
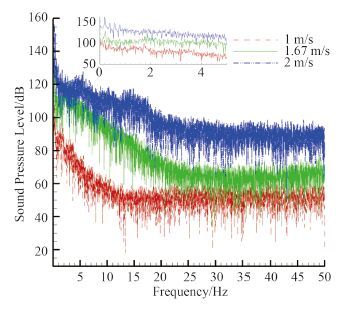
以水翼壁面上的脉动压力作为偶极子噪声源,对水翼涡激振动造成的水动力噪声进行分析,求得圆心为翼弦中点,半径为 1.5 m 圆上特征点的声压值,作出水翼流噪声的声学指向性图。从图 9 可见,由 1 m/s 增至 2 m/s 流噪声增幅较大,而后增速减缓,这是由于颤振导致振幅的不断增大导致的。且流噪声在水翼首、尾位置处较小,这是因为来流和尾流对噪声起着“掩蔽效应”,来流和尾流在靠近壁面处压力变化梯度大,流场内的不均匀波动会抵消一部分流噪声的传播,因此在这一区域流噪声数值相对较小。图 10 为特征点(2.0,0)处水翼低频段声压级对比图。可以看出,流噪声主要集中在低频区域,随着速度增大,高频成分逐渐占据主要作用,如 2 m/s 时,声级主要集中在 0~5 Hz 之间,在 3 Hz 处出现峰值,速度增至 4 m/s 时,声级则集中在 0~20 Hz 之间,并出现了多个峰值。联合频谱分析可看出,振动频率与噪声频率都随来流速度增大而增大。
|
图 9 不同流速下水翼的声学指向性图 Fig. 9 Acoustic directivity chart in various velocity |
|
图 10 不同流速下特征点声压值对比图 Fig. 10 SPL of feature points in various velocity |
本文通过数值方法分析二元水翼在紊流中的振动情况,采用弱耦合的方式联立大涡模拟湍流模型和刚体运动方程求解了水翼在 2 个自由度上的运动,在此基础上分别对比了初始攻角、刚心位置以及来流速度对振动的影响,得出以下几点结论:
1)大涡模拟方法能够较好的捕捉高雷诺数、复杂湍流中的细节,模拟出小攻角水翼绕流后完整的涡街现象。
2)水翼振动状态对系统的初始值具有依赖性,在没有扰动的情况下,水翼在 0° 攻角时始终保持微幅振动,攻角越大,振动平衡位置越偏离初始位置,且垂荡运动幅值衰减较明显。
3)航行速度对水翼振动影响较为直观,且随着速度的不断增大,水翼出现颤振现象,即振幅不衰减的自激振动。虽然水中颤振产生的条件比较苛刻,但是随流速增大而产生的振动加剧现象仍不容忽视。
4)流噪声随来流速度增大而增大,其在低频段的数值高于高频段的数值,它能够直观地反应出结构振动对流场的扰动情况。
| [1] | THEODORSEN T, MUTCHLER W H. General theory of aerodynamic instability and the mechanism of flutter[R]. NACA Report No.496, NACA, 1935. |
| [2] | HUANG R F, LIN C L. Vortex shedding and shear-layer instability of wing at low-Reynolds numbers[J]. AIAA Journal , 1995, 33 (8) :1398–1403. DOI:10.2514/3.12561 |
| [3] | JUNG Y W, PARK S O. Vortex-shedding characteristics in the wake of an oscillating airfoil at low Reynolds number[J]. Journal of Fluids and Structures , 2005, 20 (3) :451–464. DOI:10.1016/j.jfluidstructs.2004.11.002 |
| [4] |
王囡囡. 二元机翼颤振及其主动控制的研究[D]. 徐州:中国矿业大学, 2013.
WANG Nan-nan. Research on flutter and active control for two-dimensional airfoil[D]. Xuzhou:China University of Mining and Technology, 2013. |
| [5] | HENRY C J. Hydrofoil flutter phenomenon and airfoil flutter theory[M]. New Jersey: Davidson Laboratory, 1961 . |
| [6] |
余志兴. 粘性流场中的水弹性计算[D]. 上海:上海交通大学, 1999.
YU Zhi-xing. Hydroelastic dynamics in viscous flow[D]. Shanghai:Shanghai Jiao Tong University, 1999. |
| [7] |
余志兴, 刘应中, 缪国平. 二维机翼弹簧系统的涡激振动[J]. 船舶力学 , 2002, 6 (5) :25–32.
YU Zhi-xing, LIU Ying-zhong, MIAO Guo-ping. Vortex-induced vibration of two-dimensional wing-spring coupled system[J]. Journal of Ship Mechanics , 2002, 6 (5) :25–32. |
| [8] |
刘晓宙, 缪国平, 余志新, 等. 流体通过涡激振动机翼的声辐射研究[J]. 声学学报 , 2005, 30 (1) :55–62.
LIU Xiao-zhou, MIAO Guo-ping, YU Zhi-xin, et al. Research on the sound generation by flow around vortex-induced vibrated aerofoil[J]. Acta Acustica , 2005, 30 (1) :55–62. |
| [9] | CHAE E J, AKCABAY D T, YOUNG Y L. Dynamic response and stability of a flapping foil in a dense and viscous fluid[J]. Physics of Fluids , 2013, 25 (10) :104106. DOI:10.1063/1.4825136 |
| [10] | CHAE E J. Dynamic response and stability of flexible hydrofoils in incompressible and viscous flow[D]. Michigan:University of Michigan, 2015. |
| [11] |
程贯一, 王宝寿, 张效慈.
水弹性力学——基本原理与工程应用[M]. 上海: 上海交通大学出版社, 2013 .
CHENG Guan-yi, WANG Bao-shou, ZHANG Xiao-ci. Hydroelasticity——the basics with applications[M]. Shanghai: Shanghai Jiao Tong University, 2013 . |
 2016, Vol. 38
2016, Vol. 38
