2. 青岛远洋船员职业学院, 山东 青岛 266071 ;
3. 重庆交通大学 交通运输学院, 重庆 400074 ;
4. 大连海事大学 船机修造工程交通运输行业重点实验室, 辽宁 大连 116026
2. Qingdao Ocean Shipping Mariners College, Qingdao 266071, China ;
3. College of Traffic and Transportation, Chongqing Jiaotong University, Chongqing 400074, China ;
4. Laboratory of Ship-Machinery Maintenance and Manufacture for Ministry of Transportation, Dalian Maritime University, Dalian 116026, China
船舶双层底为密闭空间,其出入口狭窄,自然通风不良,易造成有毒有害气体的集聚或氧含量不足,作业人员在与外界环境相对隔离的环境中工作容易造成中毒和窒息或火灾爆炸事故的发生。在船舶修造施工作业中焊接作业工作量非常大,危险性高,现在我国修造船企业大多采用 CO2气体保护焊[1],而焊接产生大量的烟尘和有毒有害气体极易造成职业危害,在密闭舱室中进行 CO2 气体保护焊作业时产生的 CO 极易造成人体组织缺氧中毒,必须通过通风的方法排出有毒有害气体。国内学者对焊接污染进行了大量研究,蔡治平[2]等针对大型船体装焊车间焊接烟尘扩散模式理论进行了探讨,提出了焊接烟尘在室内的扩散模式和浓度分布的理论计算方法;桑丽群[3]针对焊接污染,从物理、化学污染防治两方面,提出了焊接污染的控制措施。目前国内外学者通过数值模拟的方法对焊接温度场和流场进行了分析,郑振太[4]等通过ANSYS对有强制对流效果的 CO2 气体保护焊温度场进行了数值模拟,研究了强制对流对气体保护焊温度场的影响;贾雪峰[5]等利用流体计算软件模拟研究了某高大封闭焊接车间的置换通风方案,得到了车间内焊接烟尘的浓度场分布;夏胜全[6]等建立了 CO2 气体保护焊焊接电弧三维瞬态模型,模拟出了气体保护焊焊接电弧的电场电流密度、磁场电磁力、温度和速度场的分布;戚顺顺[7]等对焊接过程中产生的 CO 气体在车间内的流动状态进行了数值模拟,分析了 CO 气体浓度场在车间内的分布规律。
陈建平运用仿真模型来分析了船舶密闭舱室在热工作业条件下的温度变化规律和通风量[8],针对船舶舱室的烟气控制方面国内学者也做了相关研究[9-10],而针对船舶密闭舱室风流流场及污染物分布的研究较少,研究船舶密闭舱室有毒有害气体分布规律,对预防有毒有害气体集聚和指导通风方案设计具有重要意义,密闭舱室的局部通风为射流通风,包括射流区和回流区,流线弯曲较大,风流流场不同于一般的厂房车间的通风,容易造成有害气体集聚。本文采用流体分析软件Fluent对典型船舶密闭舱室双层底的局部通风风流流场和有害气体 CO2 及 CO 浓度场分布进行数值模拟分析,得出风流流场和有害气体分布的一般规律。
1 双层底局部通风实验模型和模拟条件 1.1 双层底局部通风实验模型为研究船舶双层底局部通风有害气体分布规律,选取某船厂双层底分段为实验对象,在双层底舱室内部进行 CO2 气体保护焊接作业,船舶双层底分段结构如图 1所示。

|
图 1 船舶双层底分段结构图 Fig. 1 Structure block of the double bottom cell |
在船舶双层底进行 CO2 气体保护焊接作业,CO2 本身为窒息性气体,如果通风不良容易造成人员中毒窒息,由于 CO2保护气体在电弧高温的作用下的分解产生有毒气体 CO,同时 CO2 及其分解后的氧对熔化金属中的碳元素起氧化作用,经过复杂化学反应也产生一部分 CO。因此,必须通过合理的通风方式排出有毒有害气体,包括风筒布置位置、风量及风筒出口与作业点距离。
1.2 模拟条件根据双层底 CO2 焊接作业现场实际条件,CO2 焊机型号为 XD500S,CO2 流量为 15 L/min,CO 产生速率约为 170 mg/min。将风筒布置在距离作业地点 1.2 m 的舱室底部,风筒直径 0.3 m,风流流速 5 m/s。为避免风流对焊接表面 CO2 气体的直接扰动作用,将作业人员布置在风筒和作业点中间位置,距离作业地点 0.4 m,风流从风筒出流后经过人体区域饶流后携带有害气体沿舱壁向上流动,沿舱室顶部回流经人孔排出。
2 有害气体扩散数值模拟 2.1 几何模型的建立根据上述实验模型建立双层底局部通风的三维几何模型如图 2 所示,x = 3.6 m,y = 2 m,z = 2.4 m。由于作业人员对风流流场的扰动作用不能将其忽略,将人体用 x = 0.2 m,y = 0.9 m,z = 0.4 m的长方体代替,距离舱壁0.4 m,焊接作业区域紧贴舱壁。考虑到舱室内壁肋板对风流流场的扰动,将肋板假设为具有一定高度的固体壁面,风筒出口为圆形,直径0.3 m,风速5 m/s。

|
图 2 双层底局部通风的三维几何模型 Fig. 2 Three dimensional geometric model of double bottom with auxiliary ventilation |
船舶双层底焊接作业的通风风流状态为紊流,风流从风筒流出后与焊接区域的有害气体混合,引起 CO2 和 CO 气体的紊流扩散,同时由于焊接作业释放出大量热量,有害气体在浮升力的作用下自然上升,沿舱室顶部回流经人孔排出舱外。从焊接区域流出有害气体通过设置组分源项的形式表示,将 CO2 和 CO 及空气 Air 设为 3 种单独的组分,使用组分传输模型(Species Model)来模拟其混合输运过程。
对于双层底局部通风紊流扩散的稳态流动,紊流扩散的控制方程包括质量守恒方程(连续性方程)、动量守恒方程(Navier-Stokes方程)、组分传输方程及能量方程。湍流模型采用 RNG 双方程湍流模型,对于近壁面的流动采用壁面函数法处理[11]。根据上述简化和假设,控制方程可表述为:
连续性方程:
| $\quad\quad\quad\quad\quad\quad\frac{{\partial \rho u}}{{\partial x}} + \frac{{\partial \rho v}}{{\partial y}} + \frac{{\partial \rho w}}{{\partial z}} = {S_m}\text{,}$ | (1) |
动量方程:
| $\begin{aligned} & \frac{{\partial \left( {\rho uu} \right)}}{{\partial x}} + \frac{{\partial (\rho uv)}}{{\partial y}} + \frac{{\partial (\rho uw)}}{{\partial z}} = \\ & \frac{\partial }{{\partial x}}({\mu _{eff}}\frac{{\partial u}}{{\partial x}}) + \frac{\partial }{{\partial y}}({\mu _{eff}}\frac{{\partial u}}{{\partial y}}) + \frac{\partial }{{\partial z}}({\mu _{eff}}\frac{{\partial u}}{{\partial z}}) - \frac{{\partial p}}{{\partial x}}\text{,}\end{aligned}$ | (2) |
| $\begin{aligned} & \frac{{\partial \left( {\rho vu} \right)}}{{\partial x}} + \frac{{\partial (\rho vv)}}{{\partial y}} + \frac{{\partial (\rho vw)}}{{\partial z}} = \frac{\partial }{{\partial x}}({\mu _{eff}}\frac{{\partial v}}{{\partial x}}) + \\ & \frac{\partial }{{\partial y}}({\mu _{eff}}\frac{{\partial v}}{{\partial y}}) + \frac{\partial }{{\partial z}}({\mu _{eff}}\frac{{\partial v}}{{\partial z}}) - \frac{{\partial p}}{{\partial y}} - \left( {\rho - {\rho _0}} \right)g + {F_{\rm{y}}}\text{,} \end{aligned}$ | (3) |
| $\begin{aligned} \frac{{\partial \left( {\rho wu} \right)}}{{\partial x}} + &\frac{{\partial (\rho wv)}}{{\partial y}} + \frac{{\partial (\rho ww)}}{{\partial z}} = \frac{\partial }{{\partial x}}({\mu _{eff}}\frac{{\partial w}}{{\partial x}}) + \\ & \frac{\partial }{{\partial y}}({\mu _{eff}}\frac{{\partial w}}{{\partial y}}) + \frac{\partial }{{\partial z}}({\mu _{eff}}\frac{{\partial w}}{{\partial z}}) - \frac{{\partial p}}{{\partial z}}\text{,} \end{aligned}$ | (4) |
组分传输方程:
| $ \begin{aligned} \frac{{\partial \left( {\rho {c_s}u} \right)}}{{\partial x}} + &\frac{{\partial (\rho {c_s}v)}}{{\partial y}} + \frac{{\partial (\rho {c_s}w)}}{{\partial z}} = \frac{\partial }{{\partial x}}({D_s}\frac{{\partial \rho {c_s}}}{{\partial x}}) + \\ & \frac{\partial }{{\partial y}}({D_s}\frac{{\partial \rho {c_s}}}{{\partial y}}) + \frac{\partial }{{\partial z}}({D_s}\frac{{\partial \rho {c_s}}}{{\partial z}}) + {S_s}\text{;} \end{aligned} $ | (5) |
RNG
| $ \begin{aligned} \frac{{\partial \left( {\rho ku} \right)}}{{\partial x}} + &\frac{{\partial (\rho kv)}}{{\partial y}} + \frac{{\partial (\rho kw)}}{{\partial z}} = \frac{\partial }{{\partial x}}({\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial x}}) + \\ & \frac{\partial }{{\partial y}}({\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial y}}) + \frac{\partial }{{\partial z}}({\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial z}})\!\! +\!\! {G_k} - \rho \varepsilon \text{,} \end{aligned} $ | (6) |
| $ \begin{aligned} \frac{{\partial \left( {\rho \varepsilon u} \right)}}{{\partial x}} + &\frac{{\partial (\rho \varepsilon v)}}{{\partial y}} + \frac{{\partial (\rho \varepsilon w)}}{{\partial z}} = \\ & \frac{\partial }{{\partial x}}({\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial x}}) + \frac{\partial }{{\partial y}}({\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial y}}) + \\ & \frac{\partial }{{\partial z}}({\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial z}}) + \frac{\varepsilon }{k}\left( {C_{1\varepsilon }^*{G_k} - {C_{2\varepsilon }}\rho \varepsilon } \right)\text{,} \end{aligned} $ | (7) |
能量方程:
| $ \begin{aligned} \frac{{\partial \left( {\rho uT} \right)}}{{\partial x}} + &\frac{{\partial (\rho vT)}}{{\partial y}} + \frac{{\partial (\rho wT)}}{{\partial z}} = \frac{\partial }{{\partial x}}(\frac{{k}}{{{c_p}}}\frac{{\partial T}}{{\partial x}}) + \\ & \frac{\partial }{{\partial y}}(\frac{{k}}{{{c_p}}}\frac{{\partial T}}{{\partial y}}) + \frac{\partial }{{\partial z}}(\frac{{k}}{{{c_p}}}\frac{{\partial T}}{{\partial z}}) + {S_T}\text{。} \end{aligned} $ | (8) |
式中:Sm 为质量源项;Fy 为 y 方向上的动量源项;Ss 为组分的质量源项。ST 为组分的能量源项。边界条件的设置如下:
1)壁面边界条件:将巷道壁面处理为无滑移固体壁面;
2)速度入口边界条件:舱室中的风流可认为是不可压缩流体,设置风筒出口边界为速度入口边界条件,指定速度大小为风筒出口的平均流速,方向垂直于风筒出口边界,风速为 5 m/s;
3)出口边界条件为出流:人孔出口断面风流的流动是完全发展的,设置为出流边界条件;
4)源项:将焊接区域设置为流体区域,分别设置 CO2 和 CO 两种组分的质量源项、动量源项及能量源项。
3 数值模拟结果分析 3.1 风流流场分析根据上述模拟条件和边界条件假设,对双层底内 CO2 体保护焊接作业通风的风流流场进行模拟,在风速为 5 m/s 的情况下,沿舱室轴向 XY 切面上风流流场分布如图 3 所示。
|
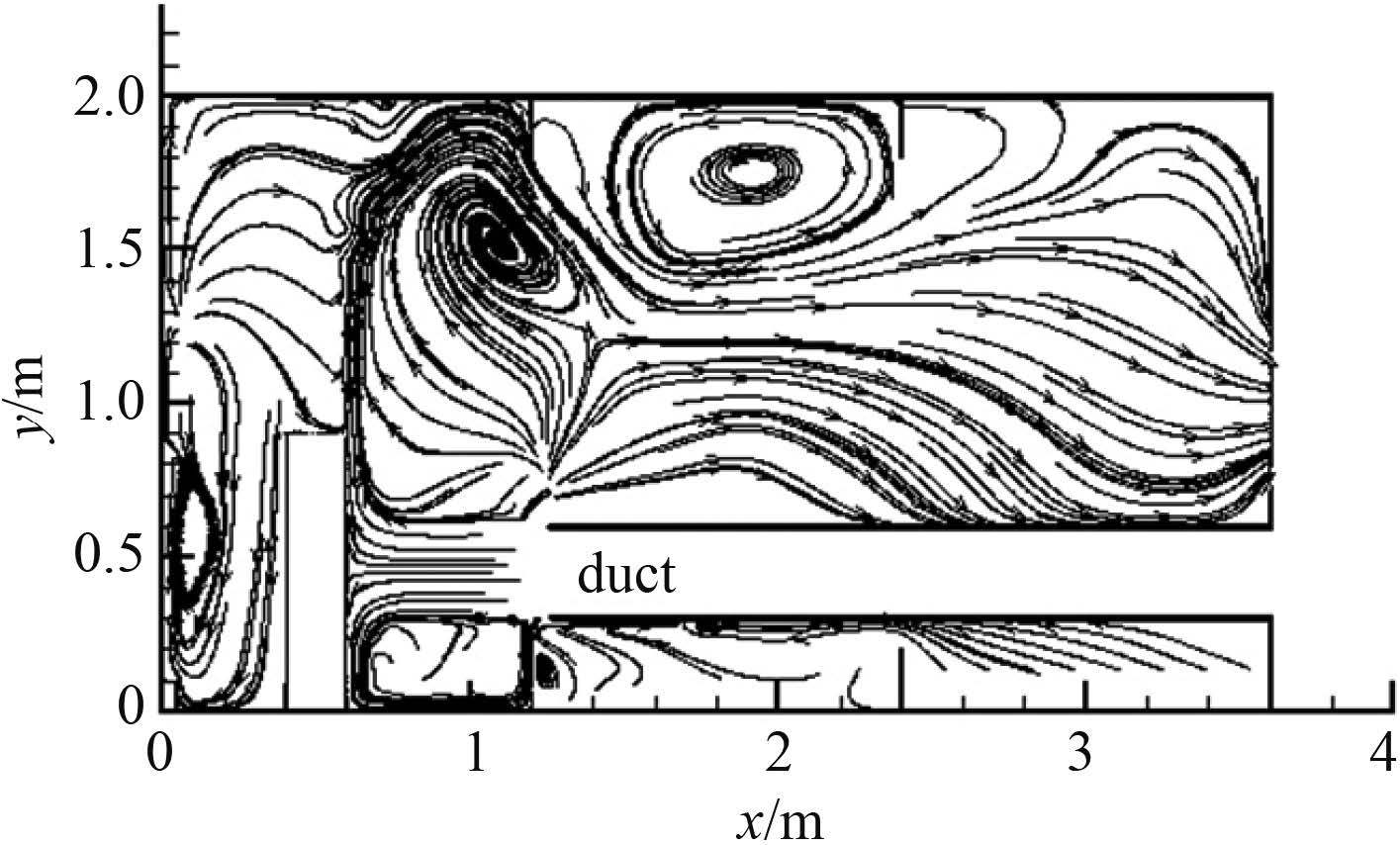
图 3 双层底轴向风流流场分布z=1.2 m Fig. 3 Distribution of stream line on section along axis z=1.2 m |
风流从风筒出流后由于人体的扰动作用,在风筒出口上部和下部区域形成涡流,焊接区域风流沿人体向下流动,与区域内的有害气体混合并沿舱室向上流动形成涡流,同时由于舱室内肋板的阻挡作用,在舱室顶部形成涡流,风流携带有害气体从人孔排出。在形成涡流的区域内容易造成有害气体的集聚,不利于有害气体的排出。
3.2 有害气体分布焊接作业人员吸入高浓度的 CO2 所出现的昏迷及脑缺氧情况,一般空气中 CO2 含量超过 1% 时,人即有轻度头晕反应;当超过3%时,开始出现呼吸困难;超过 6% 时,就会重度缺氧窒息甚至死亡;而 CO 的安全上限浓度为 30 mg/m3 或 50 ppm,超过这个浓度将影响作业人员的身体健康甚至死亡。沿舱室轴向 XY 切面上 CO2 和 CO 浓度分布如图 4 和图 5 所示。
|
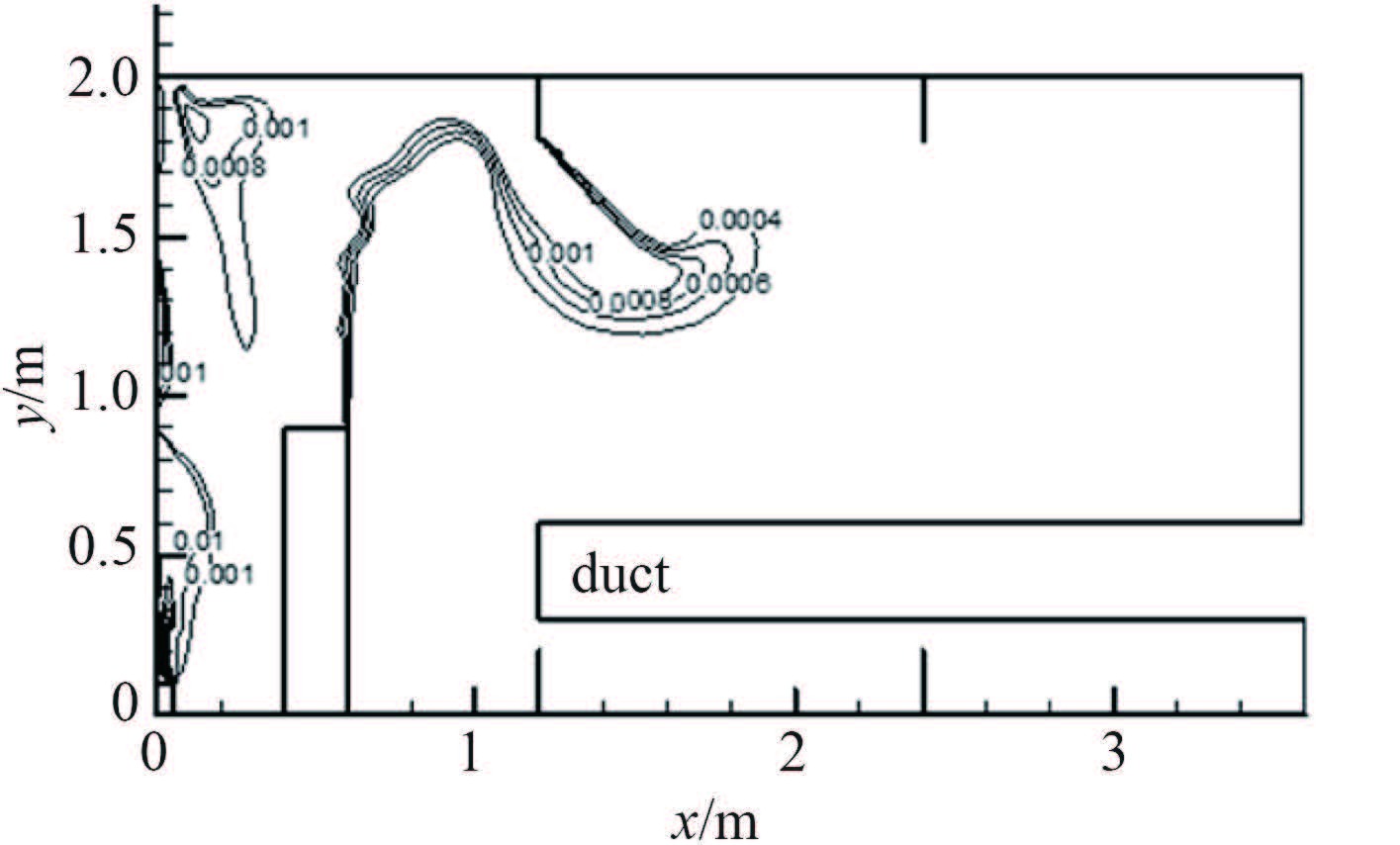
图 4 双层底轴向CO2浓度分布z=1.2 m Fig. 4 Distribution of Co2 concentration on section z=1.2 m |
|
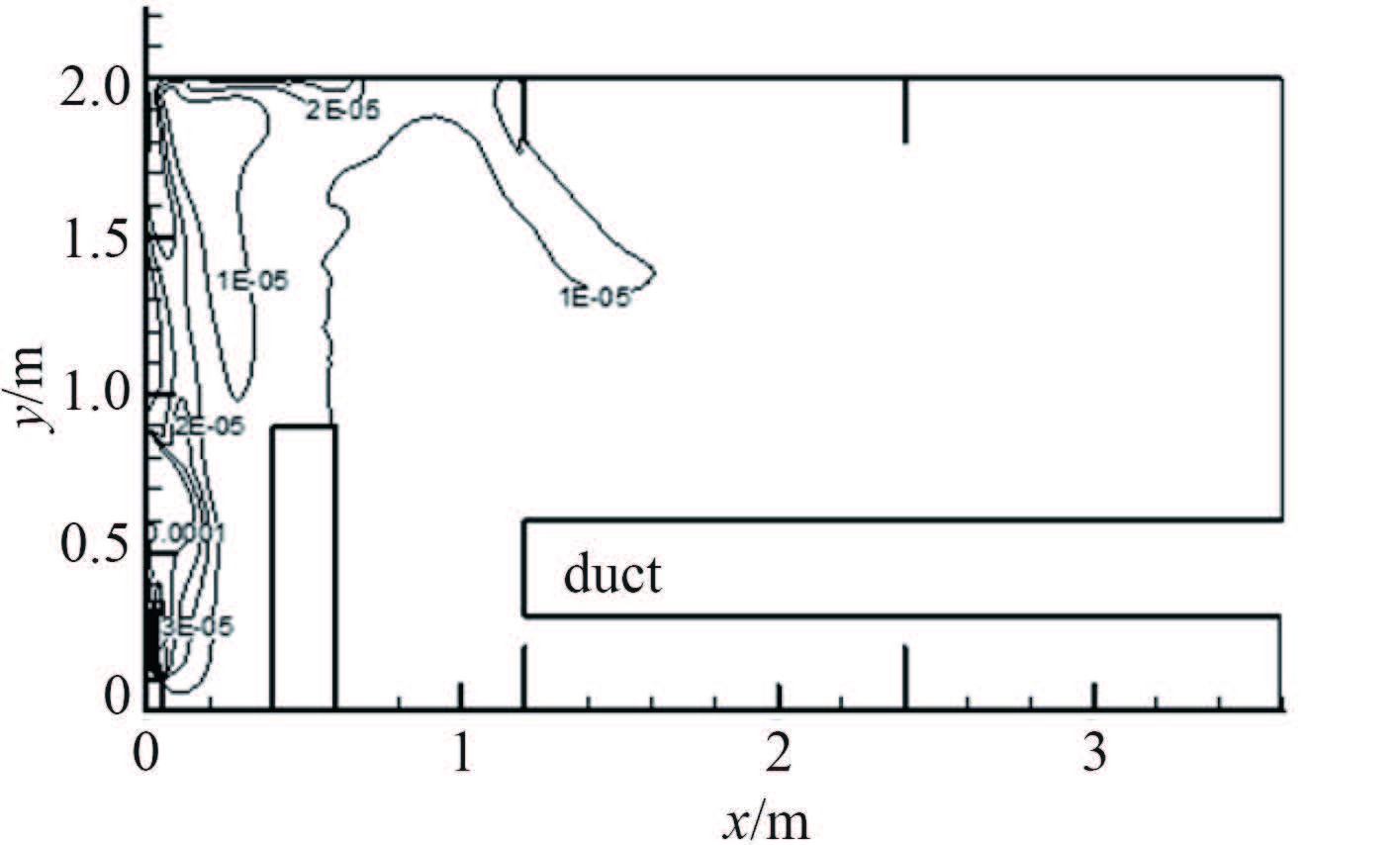
图 5 双层底轴向CO浓度分布z=1.2 m Fig. 5 Distribution of CO concentration on section z=1.2 m |
焊接区域上方距离舱壁 0.1 m 以内的区域 CO2 浓度超过 1%,而距离焊点 0.2 m 以外的区域内 CO2浓度达到 0.1%,这个区域正是作业人员头部所在的区域,能够满足安全作业的要求。舱室顶部区域风流与 CO2 充分混合,CO2浓度在 0.04% ~ 0.1% 之间,没有造成集聚。
焊接区域上方距离舱壁 0.2 m 以内的区域 CO 浓度达到 20 ppm 以上,距离舱壁 0.1 m 以内的区域 CO 浓度高达 100 ppm 以上。而距离焊点 0.2 m 以外的区域内 CO 浓度在 20 ppm 以下,作业人员在此区域内作业能够满足要求。
焊接作业人员蹲立时鼻尖距地面高度距舱底约为 0.5 ~ 0.7 m 的区域,选取 Y=0.6 m的横切面作为监测区域观测 CO 浓度的数值,如图 6 所示。
|
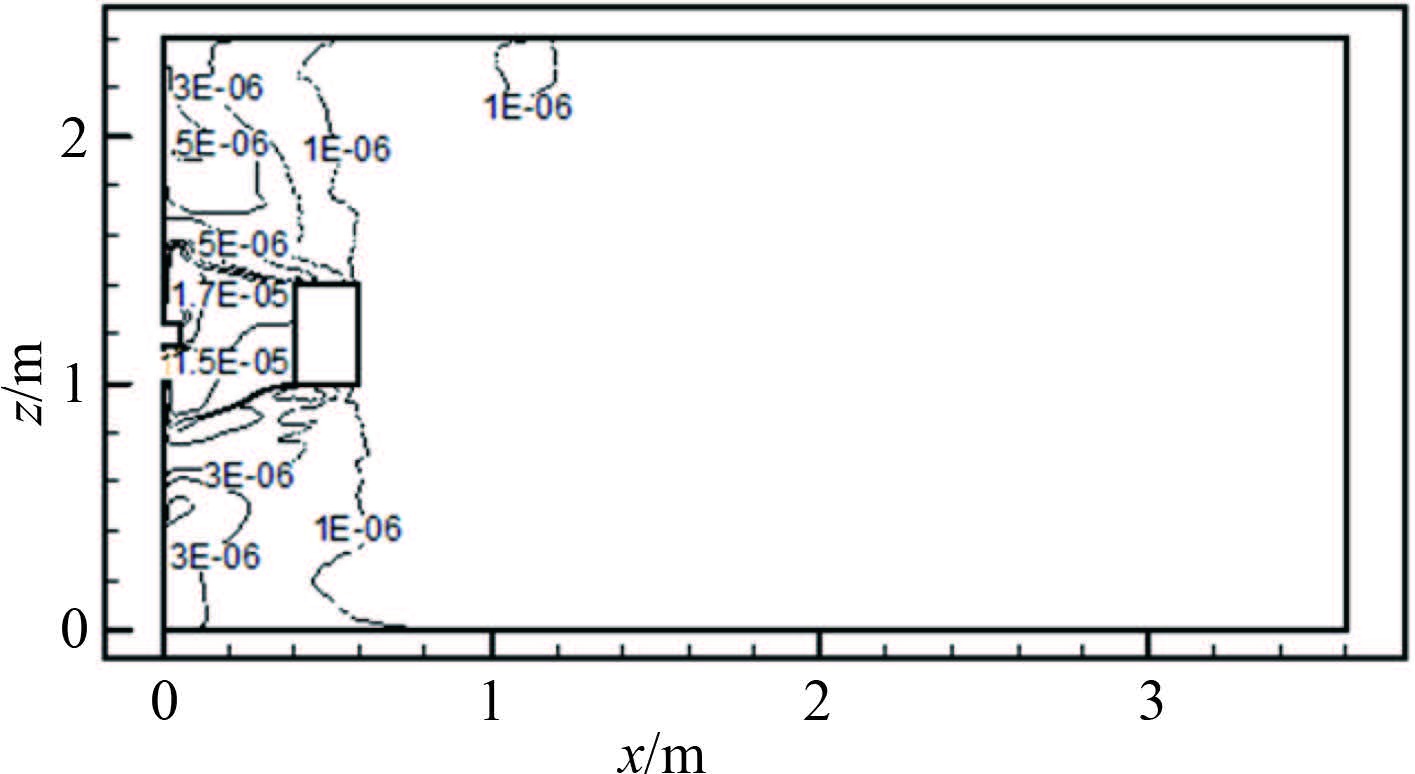
图 6 舱室横切面CO浓度分布y=0.6 m Fig. 6 Distribution of CO concentration on section y=0.6 m |
焊接区域周围距离舱壁 0.1 m 以外的区域,CO 浓度在 5 ~ 17 ppm 之间,远远低于安全上限值 50 ppm,说明焊接作业人员在此区域内作业是安全的。
在焊接作业区域周围距离舱壁 0.2 m 以外的作业区域基本是人员头部所在的区域,选取 X=0.3 m 的横断面作为检测区域观测 CO 浓度的数值,如图 7所示。

|
图 7 舱室横断面CO浓度分布x = 0.3 m Fig. 7 Distribution of CO concentration on section x=0.3 m |
在整个横断面上,距离舱底 0.5 m ~ 0.7 m 的高度上,CO 浓度在 10 ~ 40 ppm 之间,此区域为人员呼吸的区域,说明区域 CO 浓度没有超限满足作业要求;而在舱室顶部区域造成 CO 集聚,浓度超过 50 ppm。
3.3 数据对比在双层 CO2 气体保护焊实验模型中测定焊接作业人员头部鼻尖位置处的 CO 浓度,测氧测爆仪选用日本理研 GX-2003 四合一气体检测仪,测点位置为 x = 0.3 m,y = 0.6 m,z = 1.2,经多次测量求得 CO 浓度平均值为 20 ppm,数值模拟结果与实验结果基本一致,本文在数值模拟过程中将人体用长方体来代替,对模拟结果有一定的影响。
4 结 语本文针对双层底二氧化碳气体保护焊实验模型局部通风的风流流场和有害气体浓度分布进行了数值模拟,得出以下结论:
1)双层底内部在焊接作业区上方出现涡流,不利于有毒有害气体的排出,在舱室顶部也出现涡流,容易造成有毒有害气体的集聚。
2)利用设置源项的方法通过组分输运方程可以得出双层底二氧化碳气体保护焊接作业时有害气体的浓度分布情况,经数据对比数值模拟结果与实验结果基本一致。
3)风筒位于舱室底部距离焊接作业地点 1.2 m 处,风速为 5 m/s 的情况下,舱室顶部不会造成 CO2 的集聚,而在焊点正上方 CO2 浓度超过 1%,作业人员头部在此区域内有发生中毒窒息的可能性。
4)在焊点正上方区域内 CO 浓度高达 100 ppm 以上,已经远远超出安全限值,可能会造成人员中毒,在距离舱壁 0.2 m 以外的区域 CO 浓度逐渐降低;距离舱壁 0.3 m 处作业人员头部所在位置上的 CO 浓度在 50 ppm 以下,而在舱室顶部区域出现 CO 集聚现象,最高浓度达 60 ppm。
本文采用数值模拟分析的方法能够得出在局部通风情况下船舶密闭舱室内部的风流流场和有毒有害气体的浓度分布状况,根据污染物集聚情况可指导现场通风方案设计,为测氧测爆地点的选取提供理论依据,防止作业人员在密闭舱室内发生中毒窒息事故。
| [1] |
宋永伦. 我国造船焊接生产环境与安全的思考[J]. 电焊机 , 2007, 37 (6) :92–97.
SONG Yong-lun. Thought of manufacture environment and safety of shipbuilding welding[J]. Electric Welding Machine , 2007, 37 (6) :92–97. |
| [2] |
蔡治平, 徐宗古, 施介宽, 等. 大型船体装焊车间焊接烟尘扩散模式理论探讨[J]. 东华大学学报(自然科学版) , 2003, 29 (2) :27–312.
CAI Zhi-ping, XU Zong-gu, SHI Jie-kuan, et al. Theoretical study on diffusion model of welding dust in large-scale assembling-welding workshop[J]. Journal of Donghua University (Natural Science Edition) , 2003, 29 (2) :27–312. |
| [3] |
桑丽群. 焊接污染及其防治措施的研究进展[J]. 能源环境保护 , 2008, 22 (1) :18–201.
SANG Li-qun. Study on the pollution and countermeasures of welding[J]. Energy Environmental Protection , 2008, 22 (1) :18–201. |
| [4] |
郑振太, 单平, 罗震, 等. CO2气体保护焊温度场的数值模拟[J]. 天津大学学报 , 2007, 40 (2) :234–2389.
ZHENG Zhen-tai, SHAN Ping, LUO Zhen, et al. Numerical simulation of CO2 arc welding temperature field[J]. Journal of Tianjin University , 2007, 40 (2) :234–2389. |
| [5] |
贾雪峰, 刘东, 刘传聚, 等. 某封闭焊接车间的置换通风模拟研究[J]. 暖通空调 , 2010, 40 (2) :76–801.
JIA Xue-feng, LIU Dong, LIU Chuan-ju, et al. Simulation of displacement ventilation in a large-space closed welding work-shop[J]. Heating Ventilating &Air Conditioning HV &AC , 2010, 40 (2) :76–801. |
| [6] |
夏胜全, 区智明, 孙晓明, 等. CO2气体保护焊电弧温度场和流场建模与分析[J]. 焊接学报 , 2013, 34 (11) :97–1002.
XIA Sheng-quan, OU Zhi-ming, SUN Xiao-ming. Numerical simulation of temperature and flow field of CO2 gas shielded arc[J]. Transactions of the China Welding Institution , 2013, 34 (11) :97–1002. |
| [7] |
戚顺顺, 陈书锦, 朱文琪, 等. 焊接半封闭现场有害气体分布特点研究[J]. 环境科学与技术 , 2013, 36 (6L) :100–1034.
QI Shun-shun, CHEN Shu-jin, ZHU Wen-qi, et al. Study on the characteristics of harmful gas distribution of welding semi-closed field[J]. Environmental Science &Technology , 2013, 36 (6L) :100–1034. |
| [8] |
陈建平. 船舶密闭舱室热工作业温度变化及通风计算的仿真分析[J]. 船海工程 , 2010, 39 (3) :60–62.
CHEN Jian-ping. Simulation of the temperature changing and ventilation in ship's closed- in compartment[J]. Ship &Ocean Engineering , 2010, 39 (3) :60–62. |
| [9] |
张博思, 陆守香. 机械通风对船舶机舱火灾烟气控制的影响分析[J]. 船海工程 , 2013, 42 (4) :28–30.
ZHANG Bo-si, LU Shou-xiang. Analysis of the influence of mechanical ventilation on smoke control during the ship engine room fire[J]. Ship &Ocean Engineering , 2013, 42 (4) :28–30. |
| [10] |
杨志青, 王志国, 仲晨华, 等. 舰船内部通道的火灾烟气蔓延模拟及防火设计[J]. 船海工程 , 2003 (4) :1–3.
YANG Zhi-qing, WANG Zhi-guo, ZHONG Chen-hua, et al. Stimulation of fire in the passage of the warship and its fire-proofing design[J]. Ship &Ocean Engineering , 2003 (4) :1–3. |
| [11] | Fluent Inc., Fluent 6.1 user's guide[Z]. USA:Fluent Inc., 2003. |
 2016, Vol. 38
2016, Vol. 38
