0 引 言

中低分辨率 SAR 对分布式均匀目标进行成像时，因分辨单元比雷达波长大很多，回波信号在幅度和相位上出现随机变化，体现在 SAR 图像中的显著特征就是相干斑噪声，这是相干成像系统不可避免的缺陷。相干斑的存在严重影响后续 SAR 图像的解译^[1]，降斑是 SAR 图像不可或缺的部分。

相干成像体制导致 SAR 噪声不同于传统数字图像的加性噪声。Goodman 等证明^[2]，相干斑可模型化为一种乘性噪声模型，并且是非高斯的。目前相干斑滤波方法主要有空域法和变换域法。以 Lee 滤波，Kuan 滤波^[3-4]及其改进算法为代表的经典空域滤波法，通过滑动窗口估计局部统计特性，进行相干斑滤波，但是空域滤波法没有考虑 SAR 图像的结构特征，很难兼顾降斑和纹理信息的保持。以各向异性扩散降斑（Speckle reducing anisotropic diffusion,SRAD）及P-M 扩散为代表的偏微分方程滤波^[5-6]通过局部窗口内的结构检测，调节扩散系数，在一定程度上既滤除了相干斑，又保持了图像的边缘，但由于该方法需要利用局部统计特性，对于结构复杂的 SAR 图像，偏微分方程方法会出现降斑不完全或者边缘模糊的现象。近年来，非局部方法^[7-12]在 SAR 图像降噪上的应用打破了局部特性的框架，非局部均值滤波（Non-local means filter,NLMF）利用图像块之间的相似性，采取加权处理，完成相干斑滤除，但 NLMF 在加性噪声基础上推导出来，对于乘性噪声需要经过对数变换转化为加性噪声，对数变换后图像的动态范围会明显减少，降斑效果也不理想。

变换域滤波法一般通过小波变换或者超小波变换，在变换域中设计具体的滤波算法^[13-15]，变换域降斑方法是目前性能较好的算法，能够起到降斑和边缘保持的作用，但小波（超小波）正变换和逆变换需要消耗大量的计算资源，容易产生伪吉布斯现象。

如上所述，各种滤波算法都有自身的特点与缺陷，主要原因在于乘性噪声比加性噪声更难处理。全变差（Total variation，TV）正则化方法结合图像梯度信息，在图像平滑与图像修复上取得了不错的效果^[16-17]，受此启发，我们首先选择一种滤波算法对 SAR 图像进行降斑，然后使用 TV 正则化对处理后的图像进行平滑。通过比对各种算法发现，NLMF 能够对相干斑起到较充分的抑制，并且具有较好的结构保持能力。因此，本文提出一种 NLMF 与 TV 正则化结合的滤波算法 NLM-TV。首先将乘性噪声转换为加性噪声，对 SAR 图像进行区域划分，使用 NLMF 对图像进行降斑处理，然后对降斑不充分的区域进行 TV 正则化平滑处理，最终得到降斑图像。

1 加性噪声模型与区域划分 1.1 依赖于信号的加性噪声

L 视 SAR 图像 I 可表示为：

$I=R\odot \odot .$

(1)

式中，R 为场景后向散射矩阵；S 为乘性相干斑噪声；$ \odot $ 为矩阵的 Hardmard 积。若将 R，S 均视为随机量，二者是统计独立的。式（1）写为标量形式

${{I}_{i,j}}={{R}_{i,j}}+{{R}_{i,j}}({{S}_{i,j}}-1).$

(2)

式中 ${I_{i,j}},{R_{i,j}},{S_{i,j}}$ 分别为矩阵 $(i,j)$ 处的元素值。根据高斯假设和中心极限定理，通常认为 ${S_{i,j}}$ 是独立同分布的，并且服从均值为 1，方差为 $1/L$ 的伽马分布 $f(s)$。记 ${N_{i,j}} = {R_{i,j}}({S_{i,j}} - 1)$，将 N 视为噪声，则该噪声依赖于信号 R。对 R 与 N 求相关

$\left\{ \begin{align} &E[R]E[N]=0\text{,} \\ &E[RN]=E[{{R}^{2}}]E[(N-1)]=0. \\ \end{align} \right.$

(3)

式中 $E[\cdot]$ 为统计均值。式（3）表明，虽然 R 与 N 不独立，但二者不相关，因 $E[{{N}}] = 0$，二者又是正交的。则

$\left\{ \begin{align} &E[I]=E[R]\text{,} \\ &D[I]=D[R]+D[N]=D[R]+E[{{R}^{2}}]D[S]. \\ \end{align} \right.$

(4)

从式（4）中可以得出，SAR 图像的统计均值为散射强度 R 的均值，SAR 图像的统计方差由散射体 R 的方差 $D[{{R}}]$ 和噪声 N 的方差 $E[{{{R}}^2}]D[{{S}}]$ 共同组成。整理式（4）得

$E[{{I}^{2}}]=E[{{R}^{2}}](1+D[S]).$

(5)

式中 D[S] 为伽马分布所确定乘性相干斑方差。

式（4）和式（5）表明，加性噪声 N 的方差由后向散射能量 E[R²] 与乘性噪声方差 D[S] 共同决定。在 S 统计特性确定的条件下，统计量 E[I²] 反映了后向散射能量的大小，间接决定噪声水平 D[N]。E[I²] 大，则 N 的方差大；E[I²] 小，则 N 的方差小。

随着 SAR 成像幅度越来越广，一幅 SAR 图像往往由平原、山地、森林、农田及海洋等多个地域组成，这导致了噪声水平的不一致性。NLMF 在加性噪声的基础上推导而得，而式（2）~ 式（5）表明，将乘性噪声视为加性时，该加性噪声是依赖于信号的，在不同散射区域，噪声水平会有差异。所以 NLMF 处理时需要进行对数变换，将乘性噪声转为加性噪声然后进行处理，但是对数变换的非线性会使图像的动态范围以及噪声分布特性发生改变，处理后的图像并不十分理想。因此，本文中根据噪声水平将一幅 SAR 图像分为若干区域，直接将乘性噪声视为加性，使用 NLMF 进行降斑处理，并对降斑效果不好的区域进行后续修复处理。

1.2 区域划分

如前所述，统计量 E[I²] 决定了噪声水平，因此有必要依据统计量 E[I²] 将 SAR 图像分为不同的区域。记

$\overline{I_{i,j}^{2}}=\frac{1}{\left| {{\Omega }_{ij}} \right|}\sum\limits_{(p,q)\in {{\Omega }_{ij}}}^{{}}{{}}I_{p,q}^{2}.$

(6)

式中：${\varOmega _{ij}}$ 为以 $(i,j)$ 为中心的窗口；$\left| {{\varOmega _{ij}}} \right|$ 为窗口内像元数目；算子 h：${{I}} \to {{G}}$，为 I 到 G 的映射，满足 ${G_{i,j}} = \overline {I_{i,j}^2} $。

图像的边缘蕴藏着丰富的信息，为了在处理过程中更大程度的保持边缘，需要将图像的边缘单独提取出来。提取步骤如下：

1）为削弱相干斑对边缘提取的影响，将图像 I 作均值滤波，窗口大小视情况而定，一般设为 $5 \times 5$ 或 $7 \times 7$，由 “canny” 算子提取 SAR 图像的纹理与边缘。记像元索引集合为 ${\Lambda _1}$。

2）h 算子将 I 映射为 G，窗口大小与均值滤波一致。从 G 中剔除属于 ${\Lambda _1}$ 索引的像元，得到 ${{G'}} = {{G}}/{\varOmega _1}$。对 ${{G'}}$ 进行最佳直方图分割，得到强散射区像元集合 ${\Lambda _2}$ 和弱散射区像元集合 ${\Lambda _3}$。

2 NLM-TV 降斑算法 2.1 非局部均值滤波

NLMF 最先由 Buades 等在文献^[7]中提出，其突出贡献打破了传统的局部邻域框架。记 ${\mathbf{\tilde I}}$ 为滤波后的图像，有

${{\tilde{I}}_{i,j}}=\sum\limits_{(p,q)\in \Theta }{W_{i,j}^{p,q}{{I}_{p,q}}},$

(7)

式中：$\Theta $ 为 ${I_{i,j}}$ 的相似元素集合；$W_{i,j}^{p,q}$ 为依赖于 $(i,j)$，$(p,q)$ 的权重。

$W_{i,j}^{p,q}=\frac{1}{Z}{{e}^{-\frac{\left\| {{\delta }_{i,j}}-{{\delta }_{p,q}} \right\|_{\text{F}}^{2}}{h}}}.$

(8)

式中：${{{\delta }}_{{{i,j}}}},{{{\delta }}_{{{p,q}}}}$ 分别为 $(i,j),(p,q)$ 为中心的邻域块；${\left\| {} \right\|_{\text{F}}}$ 为矩阵的 Frobenius 范数；Z 为归一化因子；h 为平滑参数。

NLMF 通过设置搜索窗口与相似窗口，寻找搜索窗口内的相似块，根据相似程度进行加权处理，其核心思想是利用冗余信息达到降噪目的。平滑参数 h 控制权重的衰减程度，h 越大获得的图像越平滑，h 越小图像结构信息保持越好。

2.2 离散 TV 模型

TV 模型作为一种正则化方法广泛用于图像处理之中，在一定程度上可以起到保持边缘、图像平滑的作用。式（9）为离散 TV 降噪模型

${{\tilde{I}}_{*}}=\arg \min \left\| \tilde{I}-I \right\|_{\text{F}}^{2}+\lambda \text{TV}(\tilde{I})$

(9)

式中：$\lambda $ 为大于 0 的正则化参数；对任意的 ${{\tilde I}} \in {R^{m \times n}}$，${\text{TV(}} \cdot {\text{)}}$ 为离散全变差算子，

$\text{TV}(\tilde{I})=\sum\limits_{i=1}^{m}{\sum\limits_{j=1}^{n}{(\left| (\nabla \tilde{I})_{i,j}^{x} \right|+\left| (\nabla \tilde{I})_{i,j}^{y} \right|)}},$

(10)

式中：$\nabla $ 为离散梯度算子。

$\begin{align} &\left\{ \begin{array}{*{35}{l}} (\nabla \tilde{I})_{i,j}^{x}={{{\tilde{I}}}_{i,j}}-{{{\tilde{I}}}_{i,j+1}} &j<m, &{} \\ 0 &j=m, &{} \\ \end{array} \right. \\ &\left\{ \begin{array}{*{35}{l}} (\nabla \tilde{I})_{i,j}^{y}={{{\tilde{I}}}_{i,j}}-{{{\tilde{I}}}_{i+1,j}} &i<n, &{} \\ 0 &i=n. &{} \\ \end{array} \right. \\ \end{align}$

(11)

$(\nabla {{\tilde I}})_{i,j}^x$ 为 ${{\tilde I}}$ 在 $(i,j)$ 处的水平方向差分，$(\nabla {{\tilde I}})_{i,j}^y$ 为 ${{\tilde I}}$ 在 $(i,j)$ 处的垂直方向差分。

正则化参数的选择在 TV 模型起着均衡截断误差 $\left\| {{{\tilde I - I}}} \right\|_F^2$ 和平滑项 ${\text{TV}}({{\tilde I}})$ 的重要作用。$\lambda \to 0$ 时，截断误差 $\left\| {{{\tilde I - I}}} \right\|_F^2$ 成为控制式（9）的主要因素；$\lambda \to + \infty $ 时，式（9）的解 ${{{\tilde I}}_{{*}}}$ 为一幅充分平滑的图像。考虑到本文只对强散射区 ${\Lambda _2}$ 进行平滑，式（9）改为

${{\left. {{{\tilde{I}}}_{*}} \right|}_{{{\Lambda }_{2}}}}=\arg \min {{\left. \left\| \tilde{I}-I \right\|_{\text{F}}^{2} \right|}_{{{\Lambda }_{2}}}}+\lambda {{\left. \text{TV}(\tilde{I}) \right|}_{{{\Lambda }_{2}}}}.$

(12)

式中 ${\left. \cdot \right|_{{\Lambda _2}}}$ 为在像元集合 ${\Lambda _2}$ 上进行操作。

2.3 NLM-TV 算法流程

基于以上分析，将 SAR 图像先进行 NLMF 处理后，对降噪不完全的强散射区再进行 TV 平滑，我们称之为 NLM-TV 降斑算法。具体步骤如下：

1）将 SAR 图像噪声视为加性，按照 1.2 节相关步骤完成区域划分；

2）根据边缘与弱散射区的像素，计算边缘与弱散射区的 NLMF 平滑参数 ${h_1},{h_2}$；

3）对图像进行 NLMF 处理，边缘区域使用参数 ${h_1}$，其余区域使用参数 ${h_2}$；

4）根据处理后图像与强散射区索引，计算 TV 平滑参数 $\lambda $，对强散射区进行 TV 平滑处理；

5）融合边缘弱散射区与强散射区的处理结果，得到最终降斑图像。

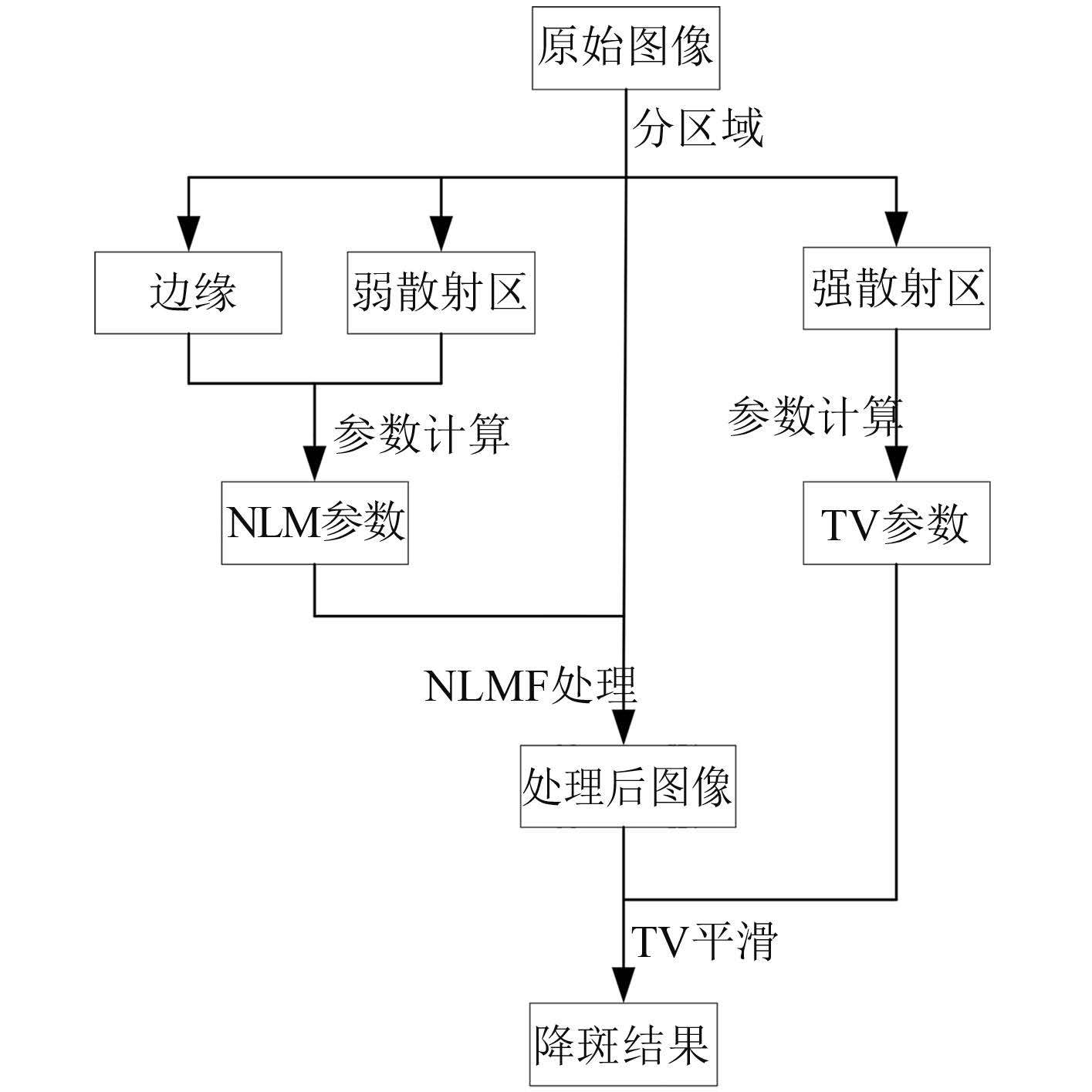
具体流程如图 1 所示。

3 相关参数选取与迭代求解算法 3.1 平滑参数 h 的选取

平滑参数 h 决定了相似度函数的衰减速率，h 越大，相似度函数的衰减速率越慢，相似图像块的权重较大，获得的图像更加平滑；相反，图像纹理越清晰。h 的大小应与图像的噪声水平相关，杨学志等^[12]通过研究得出，当 h 介于噪声方差的 0.4 ~ 0.6 倍之间时，降噪效果较好。在本文中，边缘处取比例系数为 0.4,其余区域取比例系数为 0.6。

3.2 正则化参数 λ 的选取

目前主要的正则化参数选择方法有相容性准则，无偏预风险估计、L曲线及广义交叉校验准则等，具体参见文献^[14]。本文采用广义交叉校验准则求取正则化参数 λ，对于文中 TV 模型，λ 的选取可由式（13）确定：

${{\lambda }^{*}}=\min \ \frac{(\lambda +1){{\left. {{\left\| {{G}^{*}}-I \right\|}_{\text{F}}} \right|}_{{{\Lambda }_{2}}}}}{\lambda \left| {{\Lambda }_{2}} \right|}.$

(13)

3.3 TV 模型的迭代求解算法

在求解大规模离散正则化问题时，须迭代的收敛性问题。文献中，Amir Beck ^[18]提出的一种快速投影梯度（Fast projected gradient，FPG）算法解决了 TV 的正则化降噪问题，并且证明该方法具有二阶收敛速率，可以很大程度上节省计算资源。

记 $\varPhi $ 为矩阵对 $({{B,C}})$ 的集合，其中 ${{B}} \in {R^{(m - 1) \times n}}$，${{C}} \in {R^{m \times (n - 1)}}$，满足：

$\left\{ \begin{align} &B_{i,j}^{2}+C_{i,j}^{2}1\quad i=1,\cdots ,m-1,j=1,\cdots ,n-1, \\ &\left| {{B}_{i,n}} \right|1\quad i=1,\cdots ,m-1, \\ &\left| {{C}_{m,j}} \right|1\quad j=1,\cdots ,n-1; \\ \end{align} \right.$

(14)

线性算子：

$\kappa :{R^{(m - 1) \times n}} \times {R^{m \times (n - 1)}} \to {R^{m \times n}}$，满足：

$\begin{align} &{{\left[ \kappa (\mathbf{B},\mathbf{C}) \right]}_{i,j}}={{B}_{i,j}}+{{C}_{i,j}}-{{B}_{i-1,j}}-{{C}_{i,j-1}}, \\ &i=1,\cdots ,m,j=1,\cdots ,n. \\ \end{align}$

(15)

式中：$\forall i \,=\,1,\cdots ,m;j \,=\,1,\cdots ,n$；${B_{0,j}} \,=\,{B_{m,j}} = {C_{i,0}}= $$ {C_{i,n}} = 0$。

线性算子 ${\kappa ^\text{T}}$ 为 $\kappa $ 的伴随算子，${\kappa ^\text{T}}:{R^{m \times n}} \to {\kappa ^\text{T}}:$${R^{(m - 1) \times n}} \times {R^{m \times (n - 1)}}$，满足：

$\left\{ \begin{align} &{{\kappa }^{\text{T}}}(I)=(B,C) \\ &{{B}_{i,j}}={{I}_{i,j}}-{{I}_{i+1,j}}\quad i=1,\cdots ,m-1;j=1,\cdots ,n, \\ &{{C}_{i,j}}={{I}_{i,j}}-{{I}_{i,j+1}}\quad i=1,\cdots ,m;j=1,\cdots ,n-1. \\ \end{align} \right.$

(16)

${{ P}_\varPsi }( \cdot )$ 为在集合 $\varPsi $ 上的投影算子，满足：

${{P}_{\Psi }}(I)=\left\{ \begin{align} &l\quad \quad {{I}_{i,j}}<l\text{,} \\ &{{I}_{i,j}}\quad \ l{{I}_{i,j}}u\text{,} \\ &u\quad \quad {{I}_{i,j}}>u. \\ \end{align} \right.$

(17)

其中 $u,l$ 为集合 $\varPsi $ 上的最大元素与最小元素，算法中 $\varPsi $ 应设为 SAR 图像的动态范围。

表 1 给出了 FPG 算法的实现，具体参见文献^[18]。

4 数值仿真与算法对比

以 RADARSAT-2，TerraSAR-X 实测数据对所提算法进行仿真验证，并与 SRAD，NLMF 及非下采样 contourlet 变换（Nonsubsampled Contourlet Transform，NSCT）降噪算法进行比较，通过等效视数（Equivalent number of looks，ENL）、峰值信噪比（Peak signal to noise ratio，PSNR）与边缘保持指数（Edge keeping index，EKI）这 3 个指标对不同降斑效果进行评价。

4.1 算法仿真

图 2（a）为加拿大 RADARSAT-2 于 2008 年 4 月 19 日获取的加拿大温哥华市的部分图像实验数据，HV 极化，256 × 256 像素；图 2（b）为德国 TerraSAR-X 于 2007 年 8 月 10 日获取的德国诺林根城市的部分图像，HH 极化，7 × 7 像素。

提取图像的纹理与边缘，并将其划分为弱散射区、强散射区及纹理 3 个区域，分别对应图 3 中的黑、灰、白 3 种灰度，均值滤波窗口 7 × 7。

图像经标准化处理后，对两景图像使用 NLM-TV 降噪，NLMF 滤波时取搜索窗大小 11 × 11，相似窗大小 5 × 5。RADARSAT-2 图像，弱散射区平滑参数 0.085，边缘平滑参数 0.057，正则化参数为 0.104；TerraSAR-X 图像，弱散射区平滑参数 0.088，边缘平滑参数 0.059，正则化参数 0.093。SRAD 滤波处理，迭代步长 0.05，RADARSAT-2 图像迭代 140 次，TerraSAR-X 图像迭代 180 次。 经对数变换后，NLMF 滤波的处理，取搜索窗大小 11 × 11，相似窗大小 5 × 5。RADARSAT-2 图像平滑参数 0.077，TerraSAR-X 图像平滑参数 0.080。基于 NSCT 降噪^]处理结果，分解层数为 3，各层子带数均为 8，估计 RADARSAT-2 图像噪声方差为 0.034，TerraSAR-X 图像噪声方差为 0.039。

4.2 算法对比与性能分析

为了更客观地评价降斑效果，引入 ENL，PSNR 和 EKI 三个指标，对 SAR 图像降斑效果量化分析。图 2（a）和图 2（b）中标出了 4 个区域（①，②，③，④）。①，② 区域为匀质区域，用于计算 ENL 与 PSNR；③，④ 区域包含了图像的边缘，用于计算边缘保持指数。

ENL 用来衡量图像斑点噪声的相对强度，其定义式为：

$ENL=\frac{{{\mu }^{2}}}{{{\sigma }^{2}}}.$

(18)

式中 $\mu $ 和 $\sigma $ 分别为匀质区域内统计均值与标准差。PSNR 衡量背景杂波中目标的凸显程度，定义为：

$PSNR=10{{\log }_{10}}\left( \frac{\underset{(i,j)\in \Omega }{\mathop{\max }}\,\left( \tilde{I}_{i,j}^{2} \right)}{\frac{1}{\left| \Omega \right|}\sum\limits_{(i,j)\in \Omega }{{{({{I}_{i,j}}-{{{\tilde{I}}}_{i,j}})}^{2}}}} \right).$

(19)

式中：$\mathop {\max }\limits_{(i,j) \in \varOmega } ( \cdot )$ 为区域 $\varOmega $ 内的最大值；I 为原始图像；${{\tilde I}}$ 为处理后图像。

表 2 列出了不同算法降斑处理后，两景图像 ①，② 区的 ENL 与 PSNR

分析表 2 数据，SRAD，NLMF，NSCT，NLM-TV 均能够对滤除相干斑，平滑图像起到一定的作用。在弱散射区，基于 NSCT 的滤波算法能够获得最高的 ENL，但是其代价是牺牲 PSNR。NLMF 与 NSCT 滤波在弱散射区对 ENL 提升倍数达到 13 倍以上，但在强散射区对 ENL 提升仅为 2 倍左右，原因是二者兼以加性噪声模型为基础，第一节的分析表明，当乘性噪声被当成加性噪声处理时，因噪声依赖于信号，导致了不同区域降斑效果不尽相同。SRAD 滤波通过揭示 Lee 滤波与偏微分方程滤波的内在联系，是一种以乘性噪声为基础的滤波算法，因此对强散射区，弱散射区的相干斑抑制能力较为均衡，在弱散射区与强散射区都能对 ENL 进行较大提升。NLM-TV 是 NLMF 与 TV 的融合，相对于 NLMF 具有明显的优势，具体表现为在弱散射区能够获得更高的 ENL 与 PSNR，在强散射区 ENL 提升较高，但是 PSNR 下降不明显，这表明该算法能够很大程度的滤除相干斑噪声，并保证目标不在降噪过程中被平滑处理而淹没。从表 2 的 ENL 与 PSNR 数据来看 SRAD 滤波与本文算法是 4 个算法中较为优秀的 2 个。

EKI 用来衡量经降斑处理后的边缘和纹理保持程度，EKI 定义为：

$EKI=\frac{\sum\limits_{i=1}^{N}{T(I,{{w}_{i}})}}{\sum\limits_{i=1}^{N}{T(\tilde{I},{{w}_{i}})}}.$

(20)

式中：$T( \cdot ,{w_i})$ 为图像窗口 ${w_i}$ 内梯度的最大值；N 为窗口数目；EKI 越接近 1，证明边缘保持效果越好。

从表 3 数据中不难看出，SRAD 滤波边缘保持能力最弱，NLMF 与基于 NSCT 滤波稍好，NLM-TV 边缘保持能力最强。究其原因，SRAD 算法采用的局部特性，很难将充分降噪与纹理保持完美结合。NLMF 采用的非局部方法能够较好的保持边缘与纹理特征。NSCT 因采用多尺度分析，也能具有较好的边缘保持能力。本文 NLM-TV 算法同样是非局部方法，边缘保持能力较强，区域划分后，可以将边缘单独提取出来处理，这样使得 NLM-TV 算法的边缘保持能力超过了 NLMF，而具备最强的边缘保持能力。综合表 2 和表 3 数据不难发现，NLM-TV 算法能够兼顾等效视数与边缘保持指数。

5 结 语

针对 SAR 图像乘性噪声相干斑噪声特点，提出了 NLM-TV 融合降噪算法。与以往的降斑算法不同，本文将乘性噪声视为依赖于信号的加性噪声，对不同噪声水平的区域分开处理，然后进行 TV 平滑处理。通过区域划分与算法融合，将以加性噪声为基础的 NLMF 推广到乘性噪声上。对不同区域的滤波参数进行控制，同时起到滤除相干斑与纹理保持的效果，具有实际应用价值。