2. 东部战区海军装备部信息系统处, 浙江 舟山 316000 ;
3. 中国船舶重工集团公司第七〇七研究所 九江分部, 江西 九江 332007
2. Eastern Theater Naval Armaments Department Information Systems Branch, Zhoushan 316000, China ;
3. Jiujiang Branch of the 707 Research Institute of CSIC, Jiujiang 332007, China
非线性与不确定性是船舶运动的重要特征,船舶在海上航行时受到海风、海浪和海流等海洋环境扰动作用,风浪流的作用存在强非线性和强不确定性,这造成航向会出现不可避免的不断改变[1]。船舶在以不同航速进行航行的过程中,受到海风、海浪和海流的作用效果大小很不一致,操纵机构舵机在不同航速情况下的舵面效率也不一致,低航速下舵效低而高航速下舵效高,这造成在不同航速下对船舶进行建模过程中的模型参数的不确定性,这些因素都会对实现船舶高精度和高稳定度的航向控制带来严重的困难。
经典PID控制及相关改进方法应用最为广泛,广泛应用于航空、航天、航海[2]和化工等各种工业控制中。在经典的 PID 控制中,Ki,Kp 和 Kd 分别为系统过去、现在和将来的误差信息比例,控制器综合系统的过去、现在和将来的误差信息传递给操纵结构进行调整,控制器需要的传感器信息量较少,控制器结构简单并易于实现。随着分数阶微积分学理论的发展,国内外学者对分数阶 PIλDμ 控制方法进行广泛研究[6-11],国外 Dorcak L.[7]和 Podlubony I.[8]提出 MFOPID(Fractional Order Proportion Integration Differentiation,FOPID)控制器,国内曾庆山[9]对分数阶 PIλDμ 控制器进行比较系统的仿真研究,应用在 W 平面上的根轨迹分析控制参数对系统的影响,金永顺[11]针对不同控制对象的提出 MFOPID 控制器参数鲁棒性的整定方法。分数阶 PIλDμ 控制器的阶次可以为任意实数,这种控制器结构更为精细,对系统过去、现在和将来的误差信息综合也更完整,控制效果稳定而不易发散,调节控制更为细腻,系统动态性能更良好,逐渐受到控制领域国内外学者重视。
1 船舶运动模型船舶首摇响应的线性方程式为:
| ${T_1}{T_2}\ddot r + ({T_1} + {T_2})\dot r + r = K\delta + K{T_S}\dot \delta .$ | (1) |
在操舵不是很频繁的情况下,船舶的运动可以看做一个大质量物体在舵作用下的缓慢转首运动,因此可以对船舶运动方程进行简化,野本谦作[1, 4]提出可用以下传递函数简化
| $T\dot r + r = K\delta , $ | (2) |
| $T = {T_1} + {T_2} + {T_3} .$ | (3) |
上式称为一阶 KT 方程,其中 K 称为回转性参数,T 为稳定性参数。
某型船舶首摇运动的数学模型,在航行速度 15 kn 和 24 kn 下开环 Bode 图如图 1 和图 2 所示。舵液压执行机构模型简化方框图如图 3 所示。
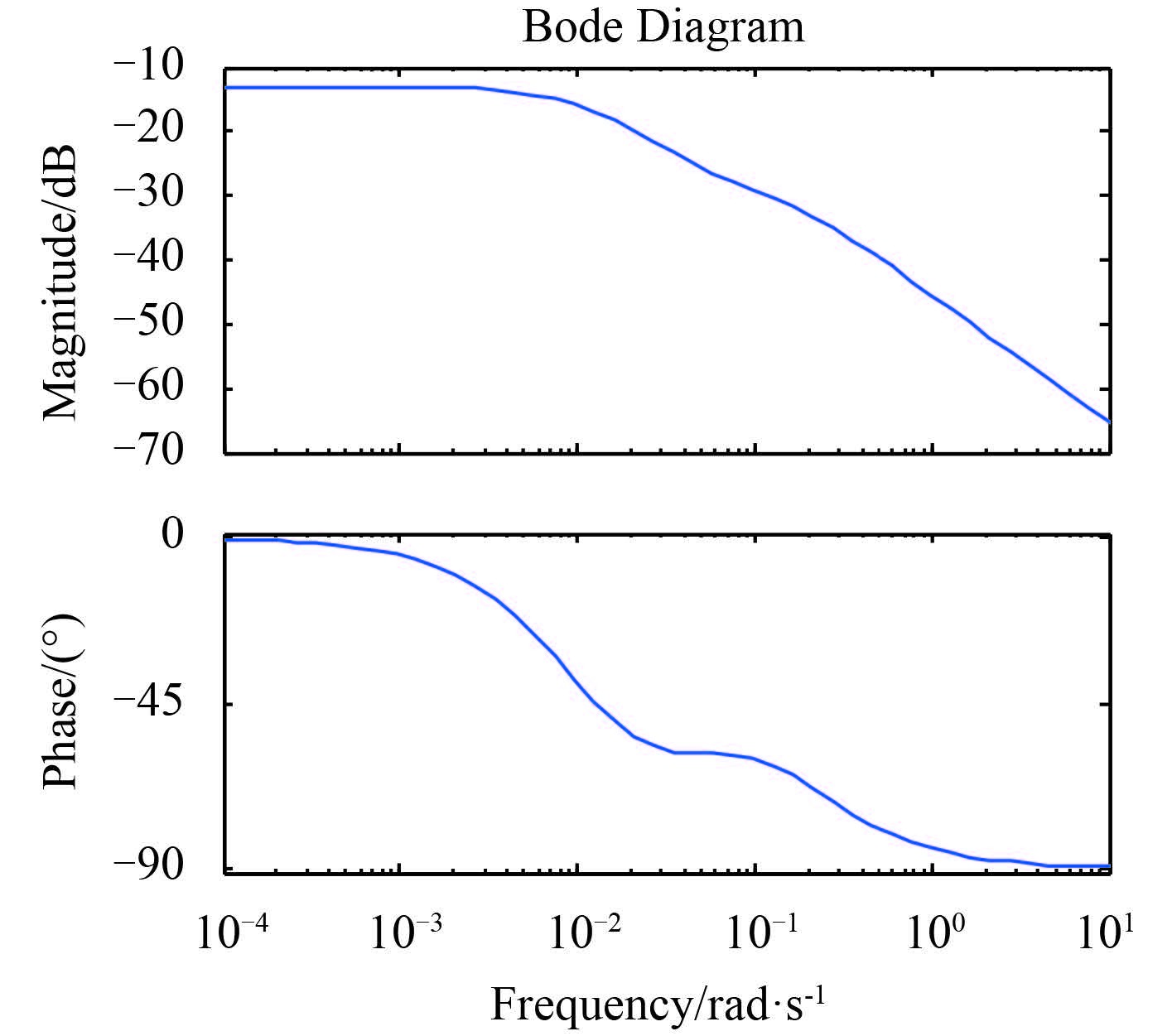
|
图 1 航速 15 kn 下艏摇运动的 Bode 图 Fig. 1 The yawing Bode diagram for velocity of 15 knots |
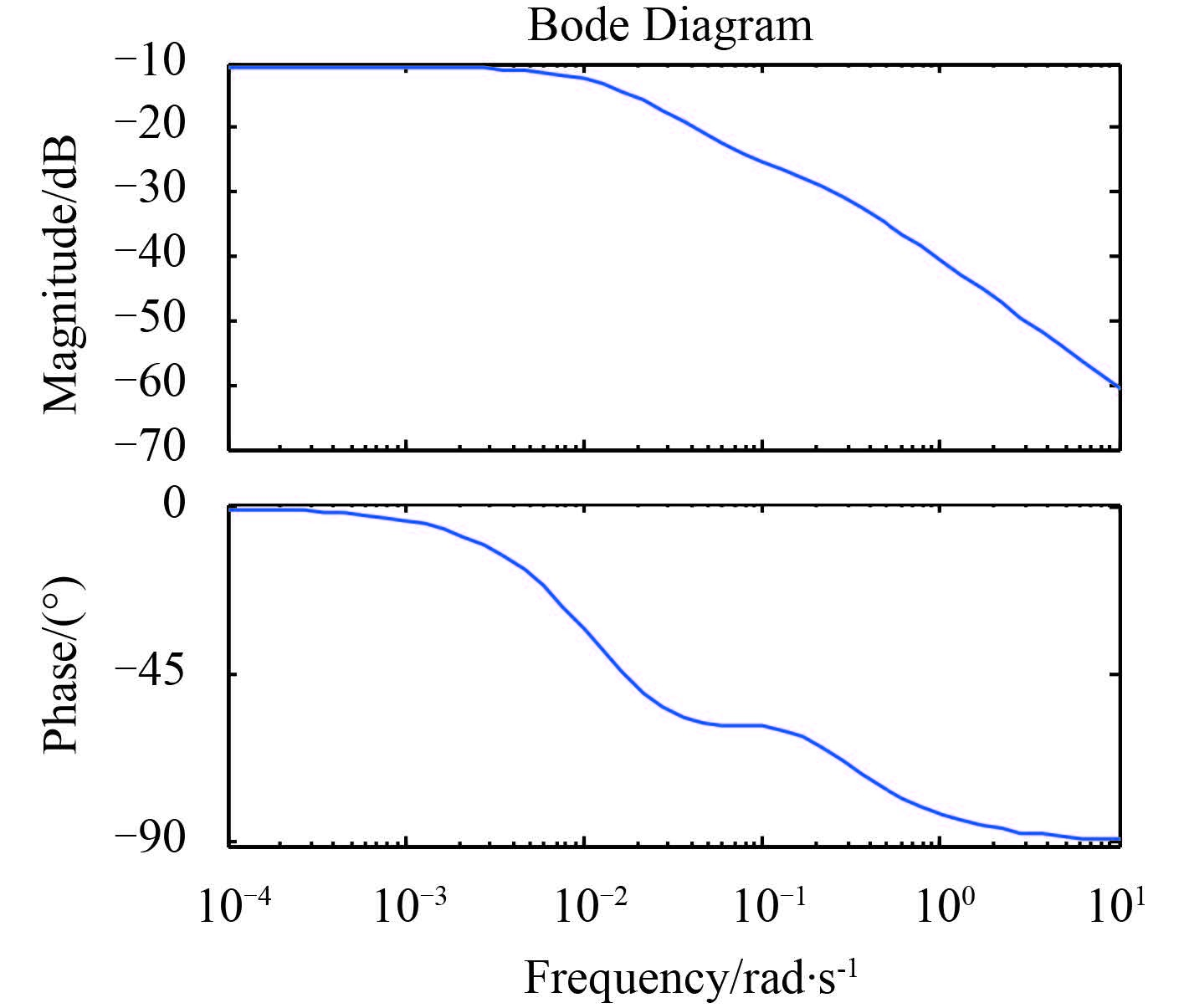
|
图 2 航速 24 kn 下艏摇运动的 Bode 图 Fig. 2 The yawing Bode diagram for velocity of 24 knots |
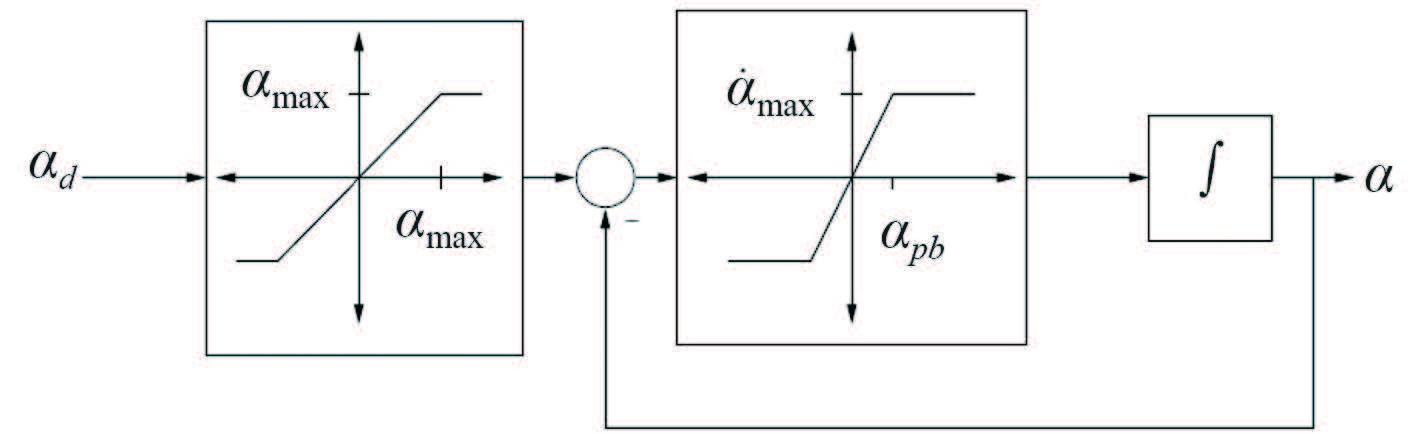
|
图 3 舵液压执行机构模型简化方框图 Fig. 3 The simplified block diagram of rudder hydraulic actuator |
舵液压执行机构的运动模型可简化为一阶惯性环节[3]形式,即
| $\frac{\alpha }{{{\alpha _d}}} = \frac{1}{{s + 1}} ,$ | (4) |
船舶因为受到海风、海浪和海流的干扰作用而产生偏移。海风产生的首摇干扰力矩[9]为
| ${N_{\omega d}} = \frac{1}{2}{\rho _a}g{({V_a} + {V_T})^2}L{C_{n\omega }}({\mu _{\omega d}}){A_L} ,$ | (5) |
式中,
海浪产生的首摇干扰力矩为:
| $\begin{array}{l} N = \displaystyle \sum\limits_{i = 1}^n {{k_1}{R_1}} \left[{\frac{{B_m^2\sin {R_2}({R_3}\cos {R_3} - \sin {R_3})}}{{R_3^2}} - } \right.\\ \left. {\displaystyle \frac{{{L_2}\sin {R_3}({R_2}\cos {R_2} - \sin {R_2})}}{{R_2^2}}} \right]{\varsigma _{ai}}\cos ({\omega _{ei}}t + {\varepsilon _{ni}}). \end{array} $ | (6) |
式中:k1 为波数;
记
| ${R_1} =\displaystyle \frac{{\rho g(1 - {e^{ - {k_1}{d_m}}})}}{{{k_1}}},$ |
| ${R_2} = \displaystyle \frac{{{k_1}L}}{2}\cos {\mu _e},$ |
| ${R_3} = \displaystyle \frac{{{k_1}{B_m}}}{2}\sin {\mu _e}.$ |
式中:ρ 为海水密度;g 为重力加速度;
海流产生的首摇干扰力矩为
| ${N_{cd}} = \frac{1}{2}\rho gV_{cd}^2L{C_{nc}}({\mu _{cd}}){A_{Ls}}.$ | (7) |
式中:ρ 为海水密度;g 为重力加速度;
定义连续的分数阶微积分算子如下[8]:
| $_aD_t^\alpha = \left\{ {\matrix{ {{{{{\rm{d}}^\alpha }} \over {{\rm{d}}{t^\alpha }}},} & {Re(\alpha ) > 0,} \cr {1,} & {Re(\alpha ) = 0,} \cr {\int\limits_a^t {{{({\rm{d}}\tau )}^{ - \alpha }}} ,} & {Re(\alpha ).} \cr } } \right.$ | (8) |
意大利数学家 M. Caputo[11]为调和分数阶微积分在数学和物理应用上的矛盾,提出新的分数阶微积分定义如下:
| $_{{t_0}}^CD_t^\alpha f(t){ = _{{t_0}}}D_t^{ - (n - \alpha )}[\frac{{{{\rm d}^n}}}{{{\rm d}{t^n}}}f(t)],$ | (9) |
其中n-1 < α ≤ n。
从 Caputo 分数阶微分定义,可以得到其任意正数阶 Laplace 变换,可表示为:
| $L{\{ _0}D_t^pf(t);s\} = {s^p}F(s) - \sum\limits_{k = 0}^{n - 1} {{s^k}{{{[_0}D_t^{p - k - 1}f(t)]}_{t = 0}}} ,$ | (10) |
其中 n-1 < p ≤ n。
类比于整数阶 PID 控制器,用微分方程表示分数阶 PID 控制器如下:
| $u(t) = {K_p}e(t) + \sum\limits_{i = 1}^k {{K_{Di}}D_{ti}^\mu e(t) + \sum\limits_{j = 1}^n {{K_{Ij}}D_{tj}^{ - \lambda }e(t)} } ,$ | (11) |
式中:λ > 0, μ > 0 为任意实数,即为分数阶控制器的微分项阶次和积分项阶次;
进行拉氏变换得到分数阶 PID 控制器的传递函数为:
| ${G_c}(s) = {K_p} + \sum\limits_{i = 1}^k {{K_{Di}}{s^\mu } + \sum\limits_{j = 1}^n {{K_{Ij}}{s^{ - \lambda }}} } .$ | (12) |
通过 Symbolic Math Toolbox 控制箱进行选择分数阶控制系统参数设计,得到控制系统 Bode 图如图 4和图 5所示。
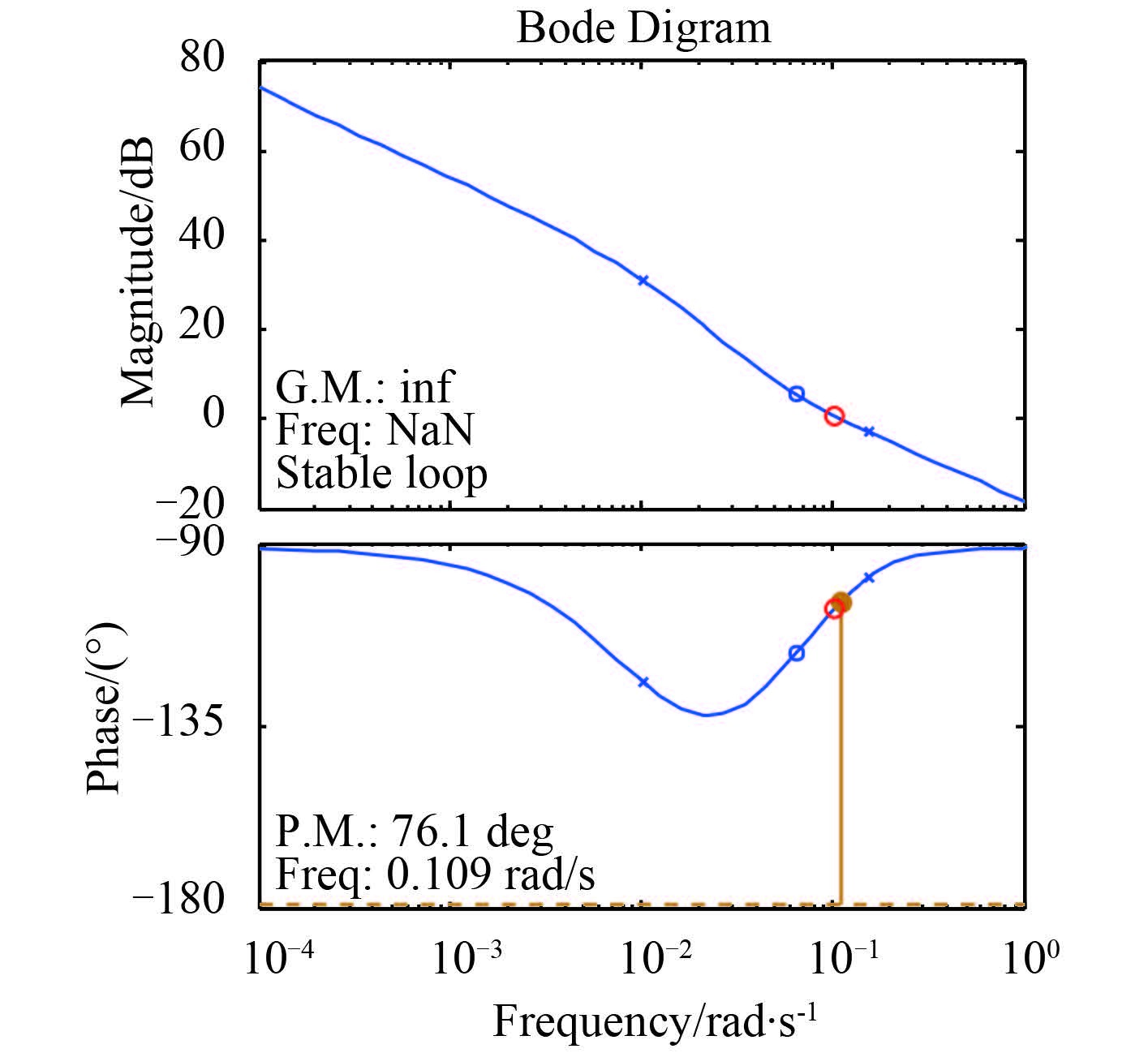
|
图 4 航速 15 kn 下闭环系统 Bode 图 Fig. 4 The Bode diagram of closed loop system for velocity of 15 knots |
|
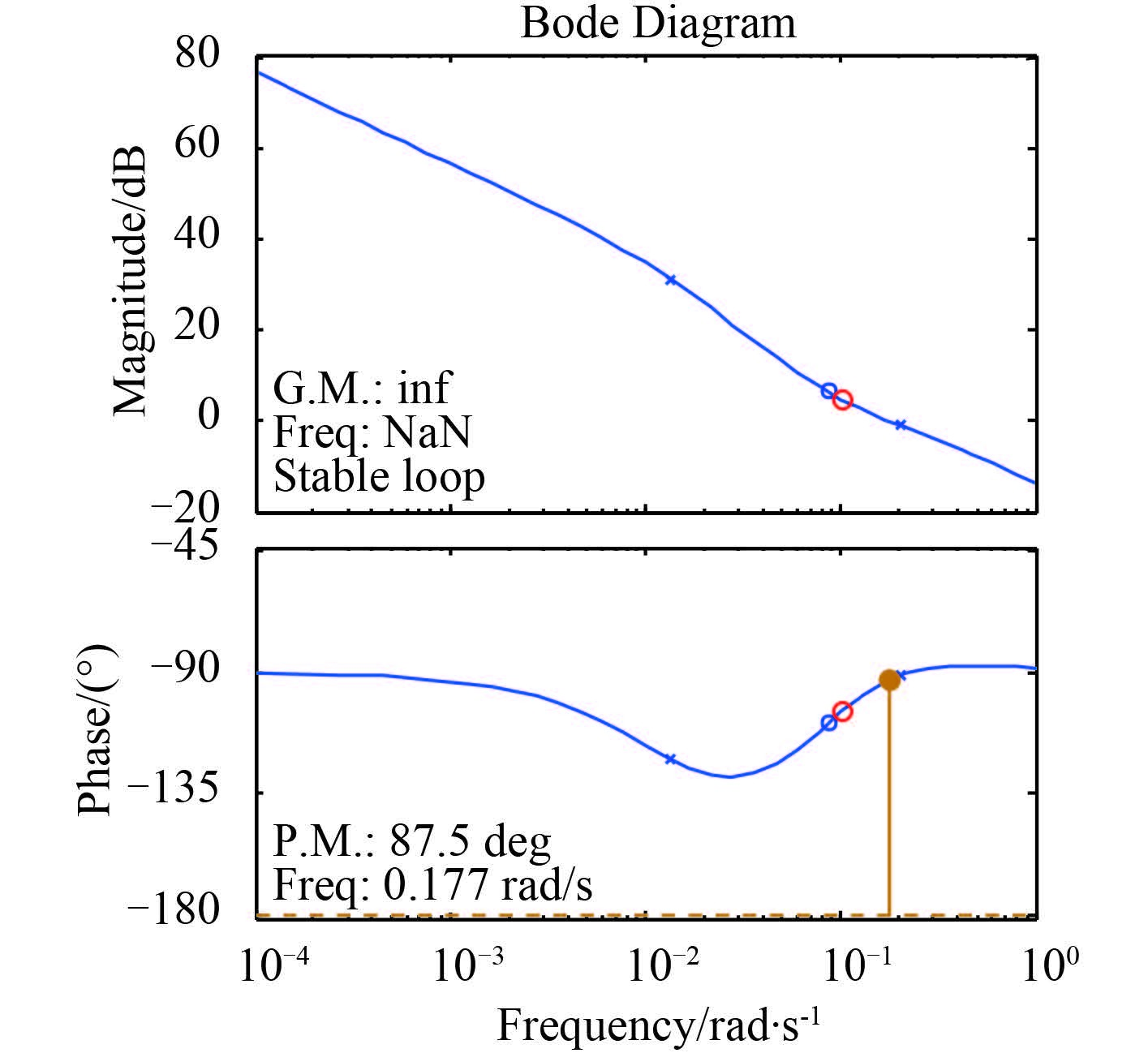
图 5 航速 24 kn 下艏摇运动的 Bode 图 Fig. 5 The Bode diagram of closed loop system for velocity of 24 knots |
如图 4 所示,在航速 15 kn 时,航向保持回路为稳定回路,截止频率为 0.109 rad/s,相角裕度为 76.1°;如图 5 所示,在航速 24 kn 时,航向保持系统为稳定回路,截止频率为 0.177 rad/s,相角裕度为 87.5°,相角裕度满足一般控制系统指标要求[12]。
4 仿真试验与数据分析将设计好的分数阶 PIλDμ 控制器参数和整数阶 PID 控制器分别对船舶非线性模型进行数字仿真,仿真中加入 6 级海风和 5 级海浪干扰扰动,为验证所设计分数阶控制器的鲁棒性和适应性,分别对船舶航速在 15 kn 和 24 kn 下进行仿真。
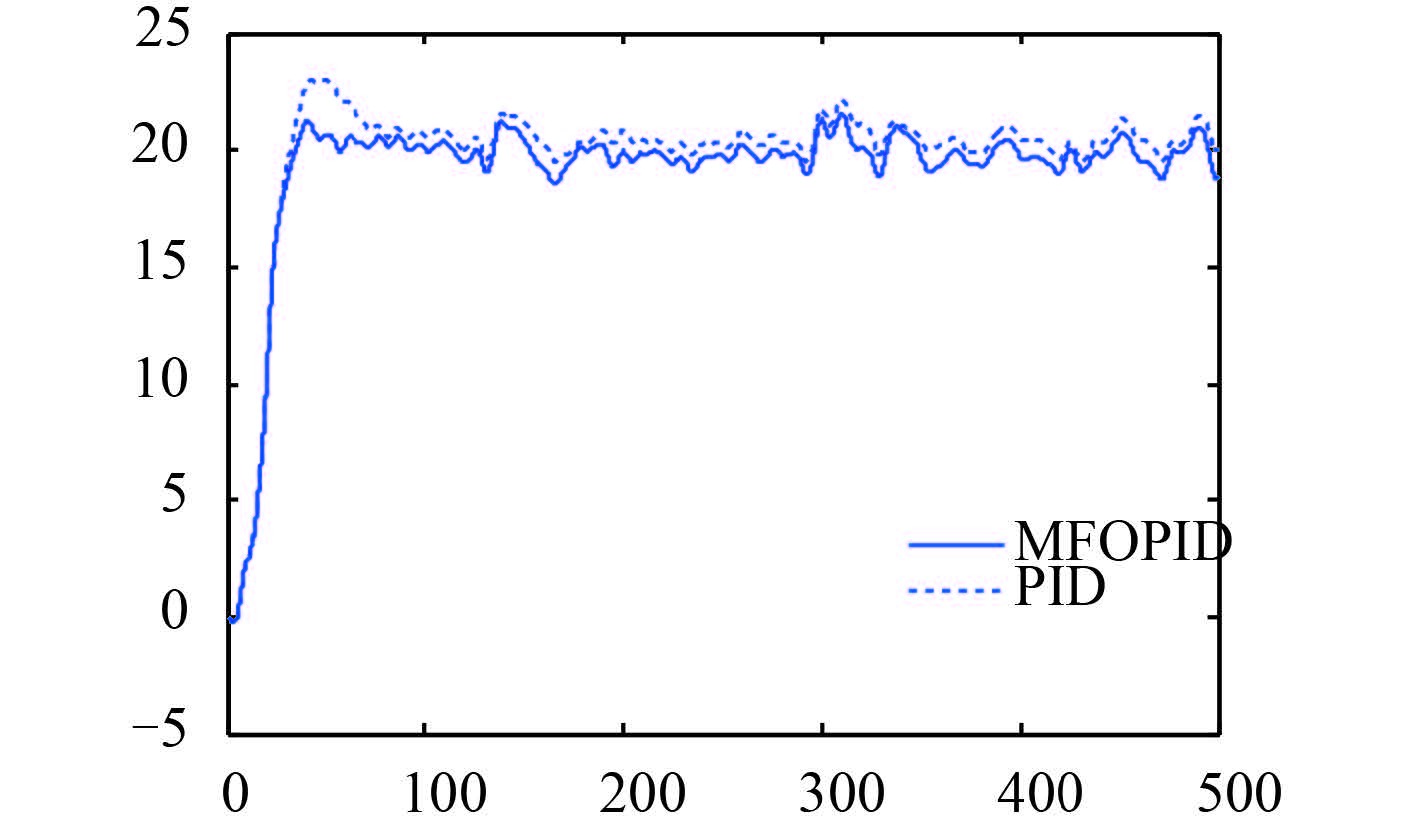
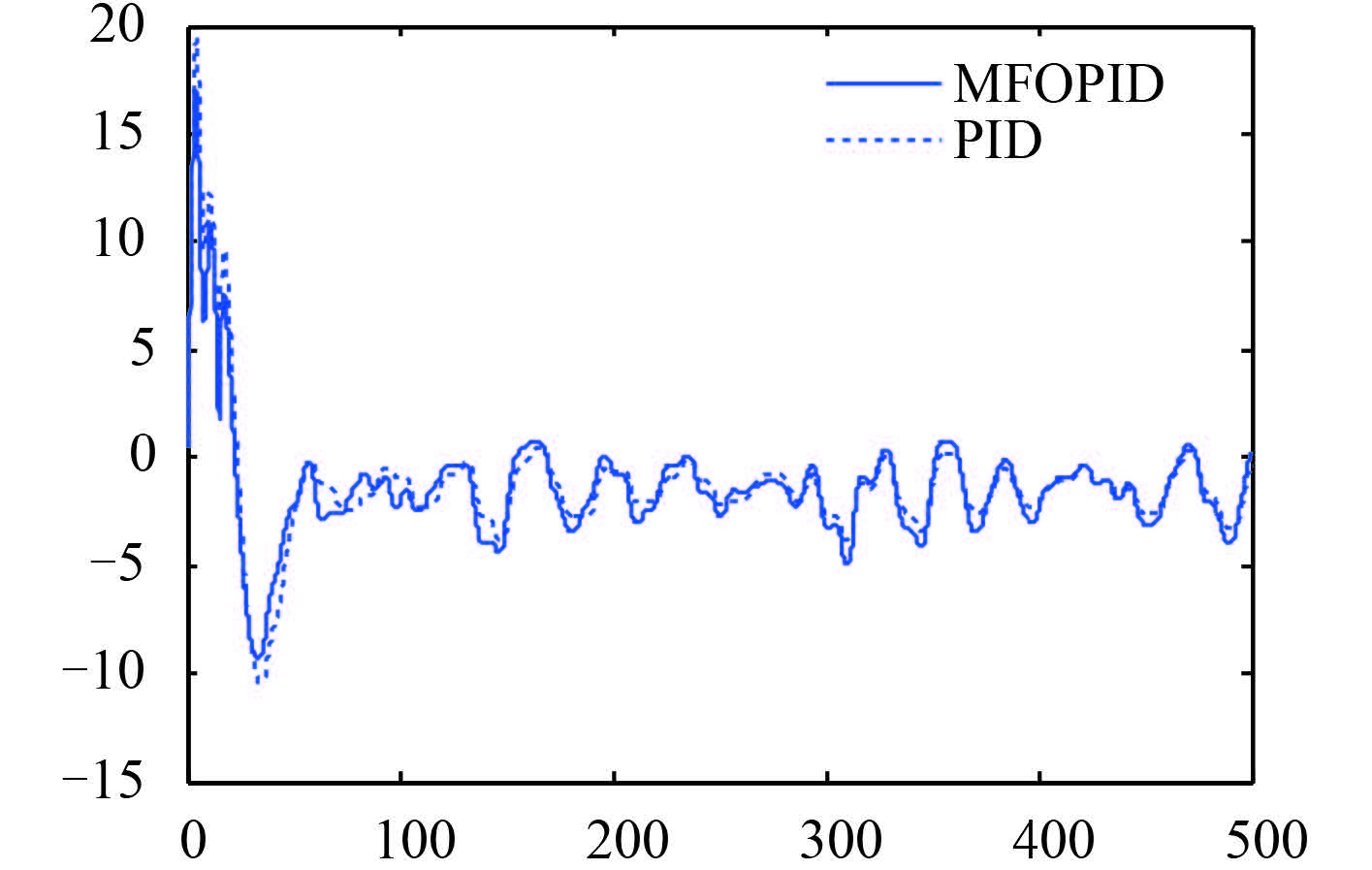
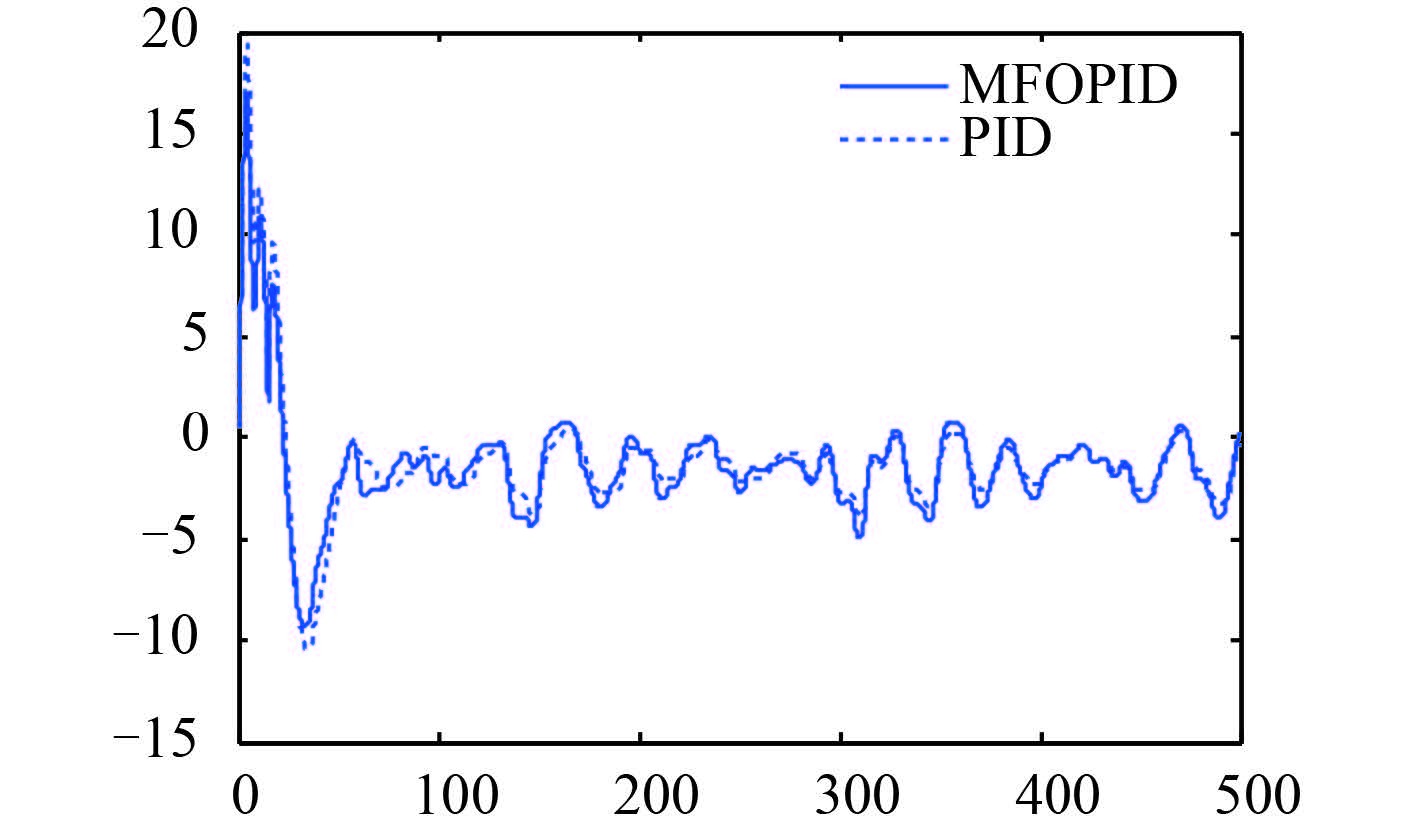
针对 6 级海风和 5 级海浪风浪干扰下某型船舶的非线性动力学模型,航速分别为低航速 15 kn 和高航速 24 kn 下进行数字仿真,仿真结果如图 6 ~ 图 9 所示。船舶在低航速 15 kn 情况下,从 MFOPID 控制和 PID 控制仿真结果看出,MFOPID 控制器下系统具有较短的调节时间和超调量,且打舵次数且打舵量的平均幅度与采用传统 PID 控制器的系统基本相当;在高航速 24 kn 下,采用 MFOPID 控制器与传统 PID 控制器相比则具优越性,采用 MFOPID 控制器,闭环系统具有更小的超调和更短的调节时间,且打舵次数与打舵量的平均幅度与采用传统 PID 控制器的系统基本相当。试验结果表明,采用 MFOPID 控制器系统,船舶在面对风浪干扰和模型摄动时也能具备比较好的航向稳定性。

|
图 6 航速 15 kn 下航向保持回路仿真响应曲线图 Fig. 6 The simulating response curves of heading-hold loop for velocity of 15 knots |
|
图 7 航速 24 kn 下航向保持回路仿真响应曲线图 Fig. 7 The simulating response curves of heading-hold loop for velocity of 24 knots |
|
图 8 航速 15 kn 下舵角输入曲线图 Fig. 8 The rudder input curves for velocity of 15 knots |
|
图 9 航速 24 kn 下舵角输入曲线图 Fig. 9 The rudder input curves for velocity of 24 knots |
本文针对某型船舶在不同航速情况下存在模型参数不确定性和风浪流的干扰问题,提出一种基于分数阶 PIλDμ 的航向控制算法并进行不同航速下仿真对比实验。仿真结果表明,该算法在满足控制精度的基础上,具有较好的动态特性和鲁棒性,对模型的摄动具有良好的适应性,可较好地应用于船舶的航向控制。
| [1] | 范尚雍. 船舶操纵性[M]. 北京: 国防工业出版社, 1988 : 30 -31. |
| [2] |
吴金波, 李天奇. 基于交叉耦合的浮筏举升系统模糊PI同步控制[J]. 舰船科学技术 , 2015, 37 (12) :33–37.
WU Jin-bo, LI Tian-qi. Synchronized fuzzy PI control for raft lifting system based on cross-coupling[J]. Ship Science and Technology , 2015, 37 (12) :33–37. |
| [3] | PEREZ T. Ship motion control:Course keeping and roll stabil-isation using rudder and fins[M]. London: Springer, 2005 : 107 -109. |
| [4] | 金鸿章, 李国斌. 船舶特种装置控制系统[M]. 北京: 国防工业出版社, 1995 : 1 -5. |
| [5] | CHISLETT M S, STR.EM-TEJSEN J. Planar motion mechanism tests and full-scale steering and maneuvering predictions for a mariner class vessel, technical report Hy-6[M]. Lyn-gby, Denmark: Hydro- and Aerodynamics Laboratory, 1965 : 1 -41. |
| [6] | 王春阳, 李明秋, 姜淑华, 等. 分数阶控制系统设计[M]. 北京: 国防工业出版社, 2014 : 5 -15. |
| [7] | DORCAK L. Numerical models for the simulation of the fractional-order control systems[R]. UEF-04-94, Kosice, 1994:arXiv:math/0204108. |
| [8] | PODLUBNY I. Fractional differential equations[M]. New York: Academic Press, 1998 : 243 -259. |
| [9] | 刘胜. 现代船舶控制工程[M]. 北京: 科学出版社, 2010 : 34 -37. |
| [10] |
曾庆山, 曹广益, 王振滨. 分数阶控制器的仿真研究[J]. 系统仿真学报 , 2004, 16 (3) :465–469.
ZENG Qing-shan, CAO Guang-yi, WANG Zhen-bin. Simulation research on fractional-order controller[J]. Journal of System Simulation , 2004, 16 (3) :465–469. |
| [11] |
金永顺.面向鲁棒运动控制系统的分数阶PID控制器设计、自整定及实验研究[D]. 长沙:湖南大学, 2011:1-7.
JIN Yong-shun. Fractional order PID controller synthesis, autotuning and experiment studies for robust motion control systems[D]. Changsha:Hunan University, 2011:1-7. |
| [12] | 卢京潮. 自动控制原理[M]. 西安: 西北工业大学出版社, 2009 : 135 -150. |
 2016, Vol. 38
2016, Vol. 38
