2. 中国船舶重工集团公司第七〇四研究所, 上海 200000
2. The 704 Research Institute of CSIC, Shanghai 200000, China
潜艇在水下发生尾水平舵卡下潜舵事故后,由于舵力的作用使艇产生首倾和下潜运动,如果没有及时采取有效的挽回措施,就可能使艇产生危险纵倾,并且艇的深度超过极限下潜深度或撞到海底。因为舵力的大小与航速平方、舵角成正比,所以高速、尾水平舵大下潜舵角卡舵事故是极其危险的情况。
本文根据分离式尾舵潜艇的特点,提出针对分离式尾舵单舵卡舵状态下的仅应用操纵面手段对潜艇进行挽回的 LQG/LTR 操纵控制技术,利用 Matlab 软件建立了相应的数值仿真模型。数值仿真结果验证了当一舷尾水平舵发生卡舵事故时,另一舷尾水平舵可以有效地对潜艇进行挽回。
1 数学模型分析对潜艇的非线性模型在定深直航状态下进行线性化,得到 14 kn 航速下的线性数学模型为:
| $\left\{ \begin{array}{*{35}{l}} \overset{\cdot }{\mathop{{{x}_{p}}}}\,={{A}_{p}}{{x}_{p}}+{{B}_{p}}{{u}_{p}},\\ \overset{{}}{\mathop{{{y}_{p}}}}\,={{C}_{p}}{{x}_{p}}. \\ \end{array} \right.$ |
式中:
在潜艇控制中,对输出向量中的量进行尺度上的变换,以使它们之间可以进行有意义的相互比较。设变换矩阵为
那么尺度变换后的潜艇模型为:
| $\left\{ {\begin{array}{*{20}{c}} {{{\mathop x\limits^ \cdot }_s} = {A_s}{x_s} + {B_s}{u_s}} ,\\ {{y_s} = {C_s}x}.\quad\quad\quad\quad \end{array}} \right.$ | (1) |
设被控对象的传递函数矩阵为
对应于卡尔曼滤波器问题,需要下面的随机动态来获得卡尔曼滤波器增益:
| $\left\{ {\begin{array}{*{20}{c}} {\mathop {{x}}\limits^{{.}} = {{Ax}} + {{\xi }}},\\ {{{y}} = {{Cx}} + {{\theta }}} . \end{array}} \right.$ |
式中:
| $0=A\sum{+\sum{{{A}^{\text{T}}}+\Xi -\sum{{{C}^{\text{T}}}{{\Theta }^{-1}}C\sum{{}}}}},$ |
滤波器增益
对于最优状态反馈调节器问题,有控制代数黎卡提方程(CARE):
| $0 = - {{KA}} - {{{A}}^{\rm{T}}}{{K}} - {{Q}} + {{KB}}{{{R}}^{ - 1}}{{{B}}^{\text{T}}}{{K}},$ |
式中:R 为控制输入加权矩阵;Q 为状态变量加权矩阵。那么控制增益
设
| $\begin{align} & \sigma ({{T}_{KF}})=\sigma (C{{(sI-A)}^{-1}}H)\approx \\ & \frac{1}{\sqrt{\mu }}\sigma (C{{(sI-A)}^{-1}}B)=\sigma ({{T}_{FOL}}). \\ \end{align}$ |
因此可以通过调节参数 μ 使得
设状态变量加权矩阵
那么LQG/LTR控制器的传递函数矩阵为:
| $\begin{align} & K(s)=G{{(sI-A+BG+HC)}^{-1}}H= \\ & G(sI-{{(A-BG-HC)}^{-1}})H. \\ \end{align}$ |
在时域中,设控制器的状态向量为
| $\left\{ {\begin{array}{*{20}{c}} {\mathop {{z}}\limits^{{.}} = ({{A}} - {{BG}} - {{HC}}){{z}} - {{H}}e},\\ {{{u}} = - {{{G}z}}} .\qquad\qquad\qquad\quad\, \end{array}} \right.$ |
式中:u 为控制输入;e 为误差向量。
2.2 基于潜艇模型的 LQG/LTR 设计针对模型(1)进行 LQG/LTR 控制器的设计,为确保系统的零稳态误差,必须在被控对象和控制器间设置合适的积分器,这一点可以通过对被控对象的状态增广方法来实现。也就是说,将增广了积分器的被控对象视为广义的被控对象,然后针对广义被控对象设计 LQR/LTR 控制器。在 LQR/LTR 控制器设计完成后,将积分器纳入所设计的控制器即可,这样得到的控制器才是最终设计的控制器。
对每个控制通道均增加一个积分器,则广义被控对象的维数由 10 维增加到 14 维,并可由下面的动态来描述:
| $\left\{ \begin{align} & \overset{\cdot }{\mathop{\text{ }x}}\,=Ax+Bu,\\ & y=Cx. \\ \end{align} \right.$ |
式中:
对状态增广后的对象进行 LQG/LTR 控制器的综合,选择合适的参数并经反复调试得到 LQG/LTR 控制器的参数。
3 闭环控制系统仿真分析当航速 14 kn,且潜艇初始状态为定深直航状态时,在 t = 100 s 时潜艇的尾左水平舵突然卡舵且打在最大下潜舵角 30 °。之后潜艇的方向舵、尾右水平舵和首水平舵协调操作对潜艇卡舵事故进行挽回,保持潜艇的深度。图 1 给出了在分离式尾舵单舵卡舵状态下的潜艇深度曲线。图 2 ~ 图 5 分别为方向舵、尾左右水平舵和首舵舵角曲线。
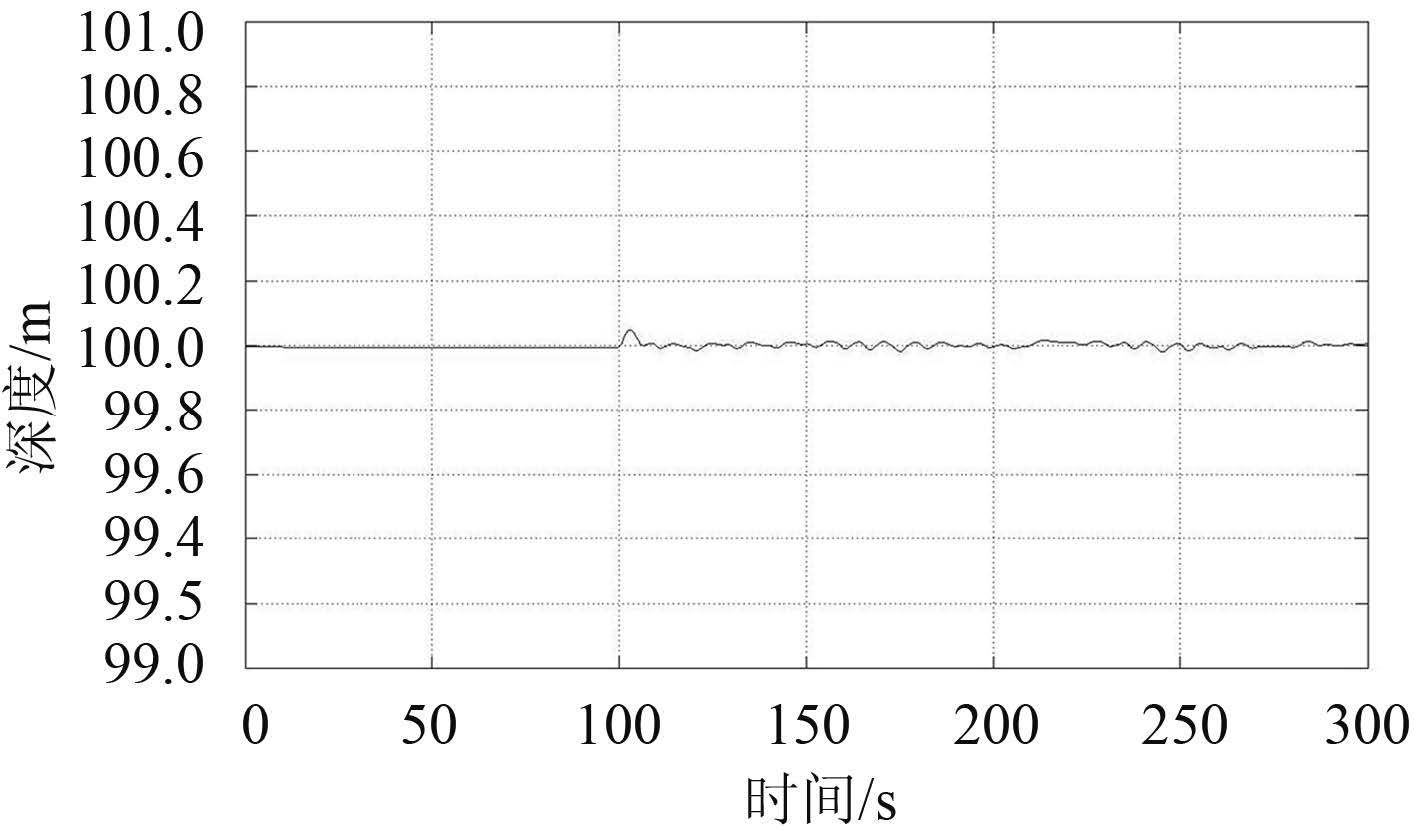
|
图 1 14 kn 航速潜艇的深度 Fig. 1 The depth of submarine under 14 kn |
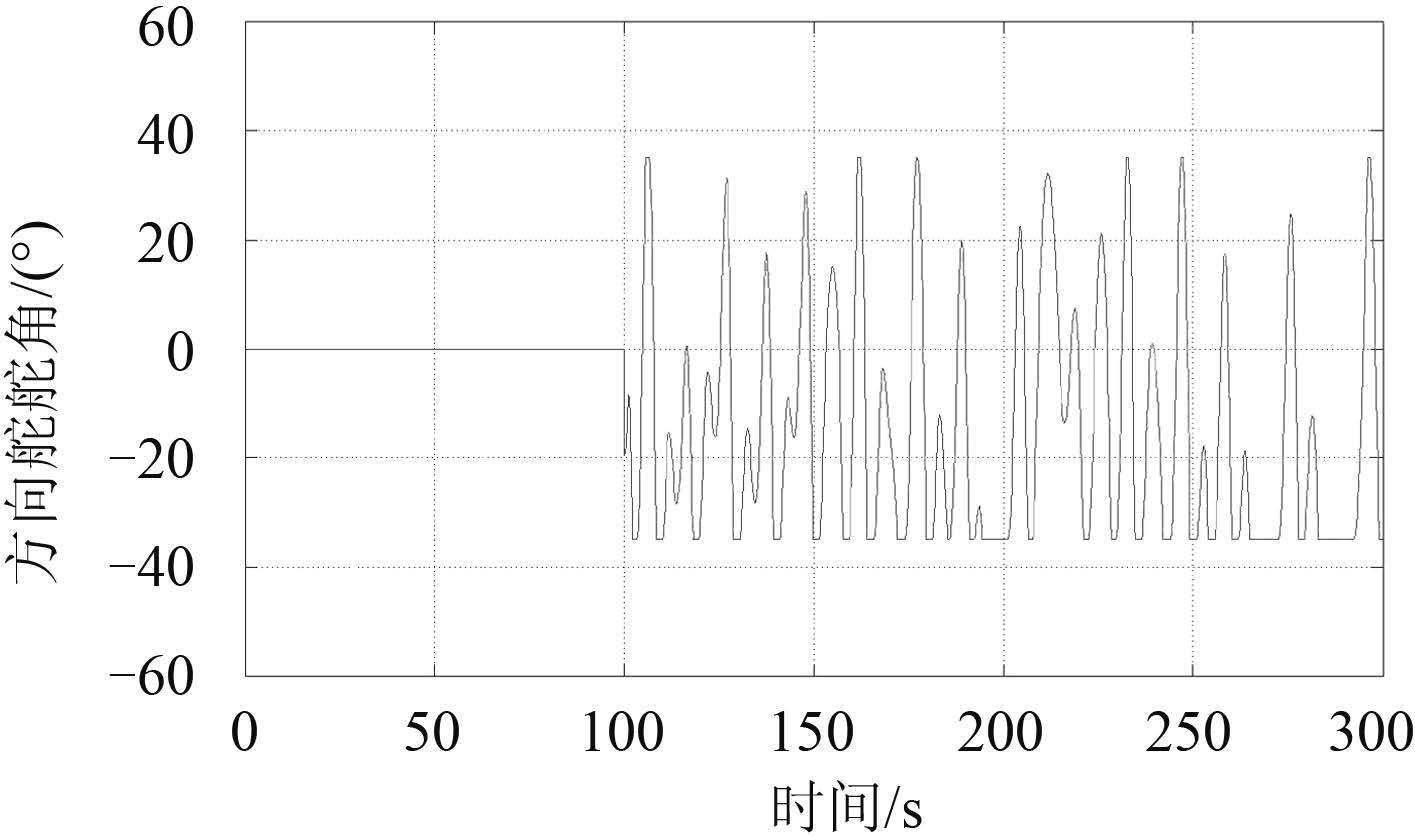
|
图 2 14 kn 速潜艇的方向舵舵角 Fig. 2 The rudder angle of submarine under 14 kn |
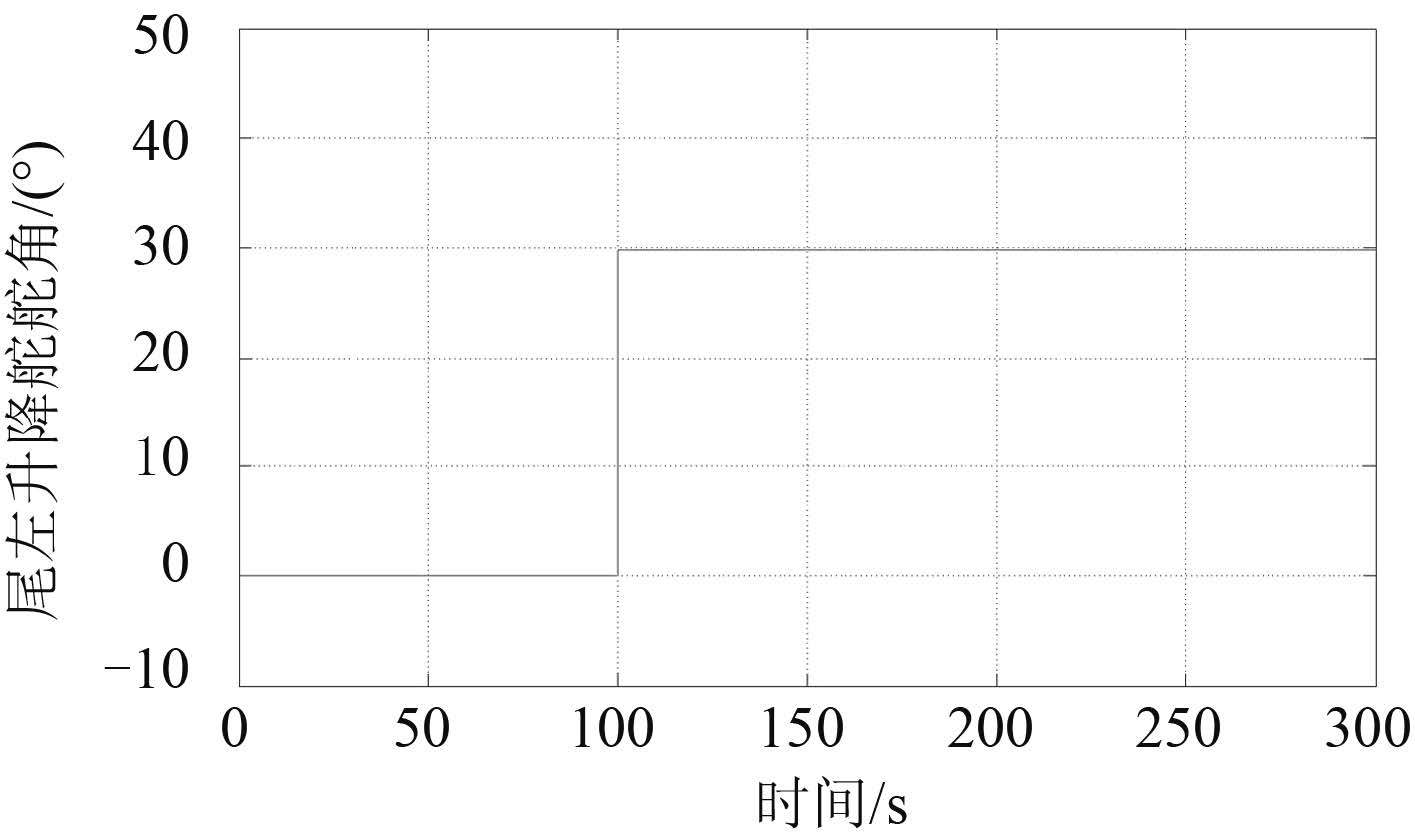
|
图 3 14 kn 速潜艇的艉左水平舵舵角 Fig. 3 The left hydroplane angle of submarine under 14 kn |
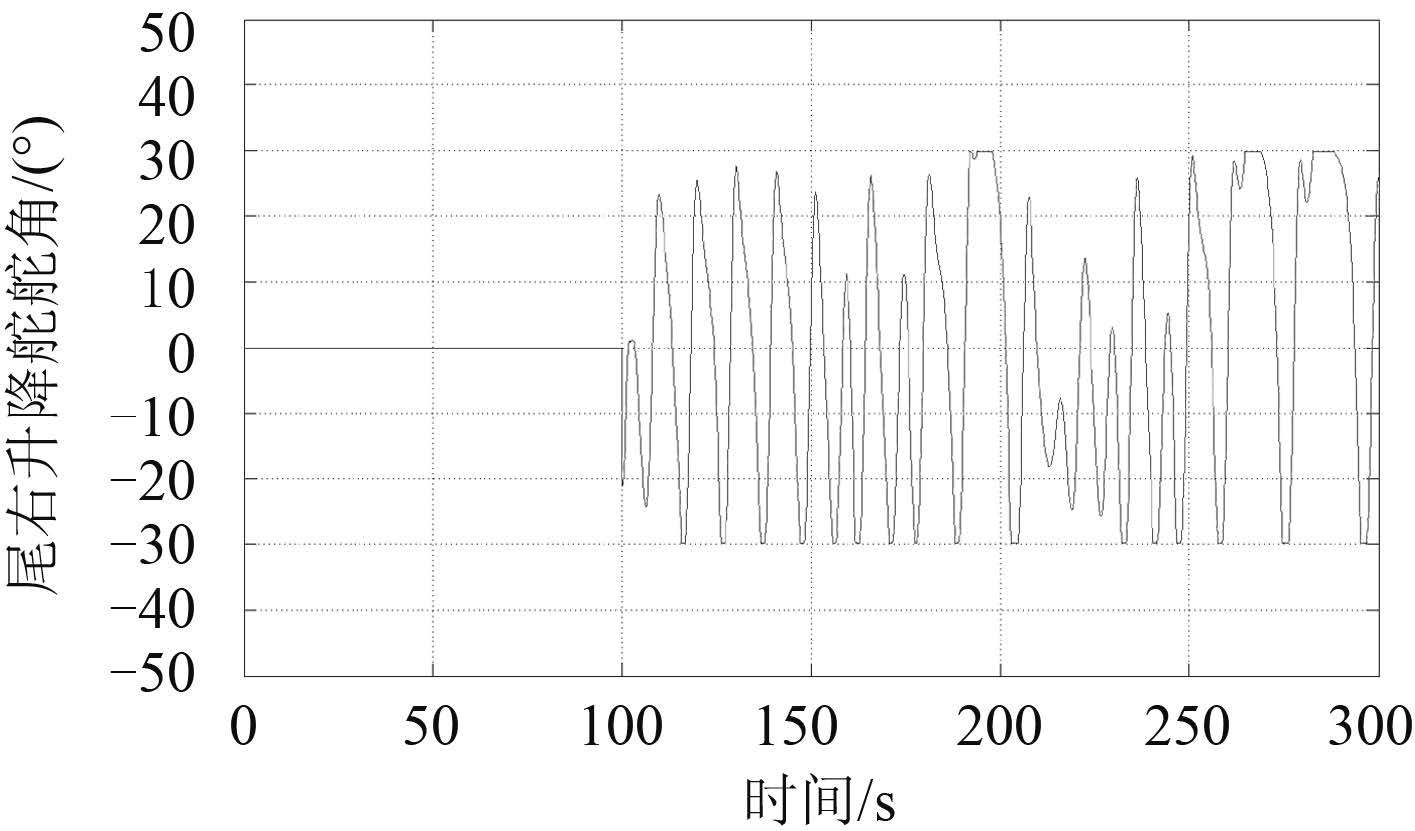
|
图 4 14 kn 速潜艇的艉右水平舵舵角 Fig. 4 The right hydroplane angle of submarine under 14 kn |
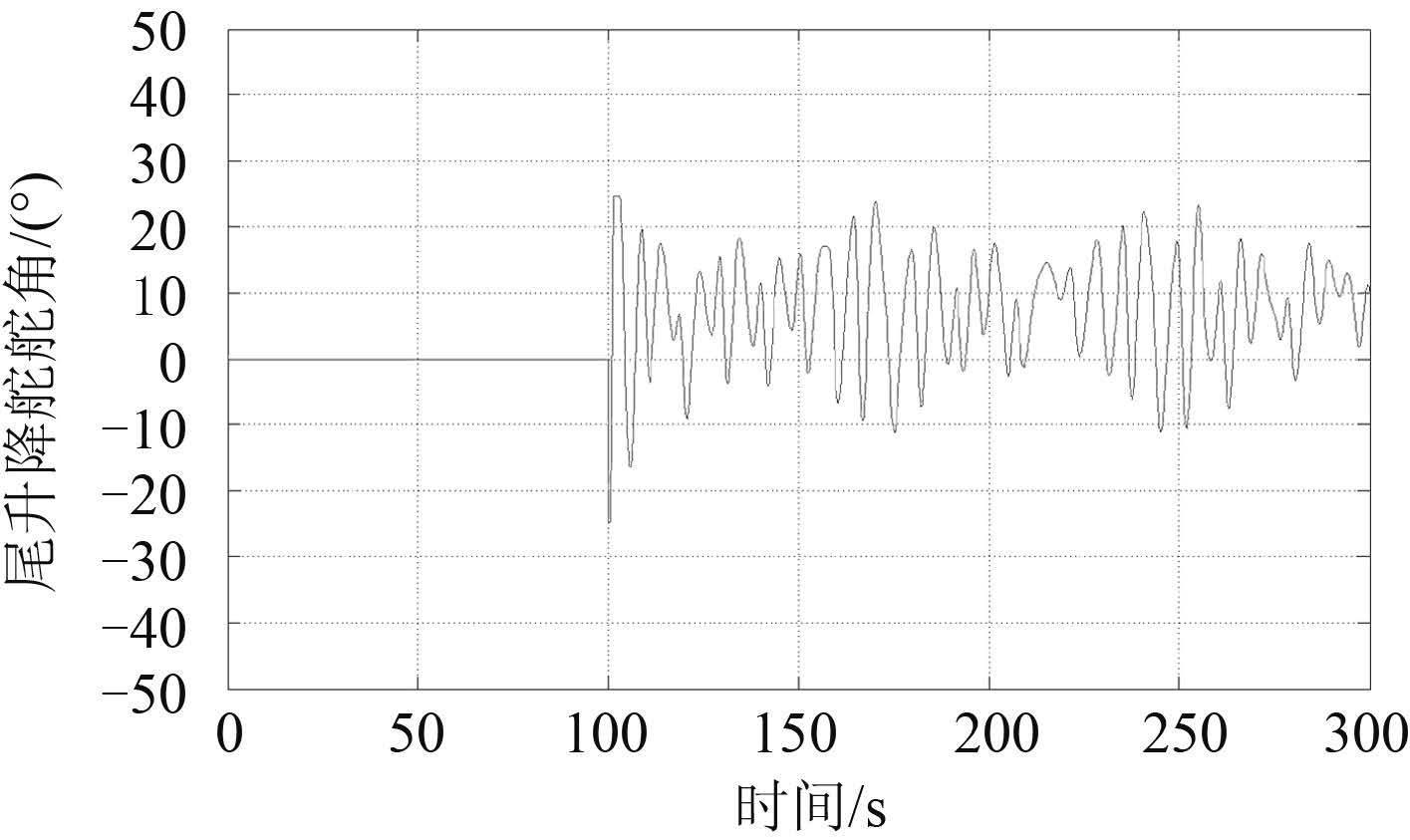
|
图 5 14 kn 速潜艇的艏水平舵舵角 Fig. 5 The fore hydroplane angle of submarine under 14 kn |
由图 1 可知,在分离式尾舵单舵卡舵状态下的挽回过程中,潜艇能够保持定深,并在经过瞬态之后稳定在 100 m 附近的很小范围内,深度变化极小。
4 结语上述研究和仿真结果可知,对于分离舵来说,卡舵不再是一种十分危险的事故,并且艇在水下正常航行时,首、尾水平舵都是以保持深度方式操纵,所以一舷尾分离舵发生事故后,只需及时采取协调操舵及减速措施挽回,艇的深度和纵倾的变化都较小。
| [1] | 施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995 . |
| [2] | 孙元泉. 潜艇和深潜器的现代操纵理论与应用[M]. 北京: 国防工业出版社, 2001 . |
 2016, Vol. 38
2016, Vol. 38
