为抑制机械或结构的振动传递到基础,隔振技术在工程中已经得到了广泛应用。如今,线谱已成为现代被动声呐在水声对抗中检测、跟踪和识别目标的主要特征信号,因而降低机械设备辐射噪声中的线谱成份已是目前隔振技术研究的热点之一[1]。
常规减振方法大多是按线性理论设计[2],而线性隔振技术只能降低辐射噪声中特征线谱成分的幅值,而不能改变其频谱特征,对低频线谱的隔离能力也非常有限。近年来,各国学者在非线性隔振技术上进行了大量的研究工作,针对线谱是潜艇声隐身性能的主要危害并难以消除的这一问题,楼京俊等[3]利用非线性隔振系统出现混沌状态时功率谱呈现连续谱且强度下降这一特征,提出可应用于潜艇结构噪声线谱控制的混沌隔振方法[4-8]。研究表明,非线性隔振系统处于混沌状态时有很好的隔振效果,并且能够明显降低结构噪声中的线谱成分,因而应用前景非常广泛[9]。
由于混沌隔振基本理论已完全不同于线性隔振基本理论,要是能将混沌控制理论与机械隔振技术相结合,那么既能够使现代隔振理论得到创新,又能够推动国内外潜艇机械噪声控制技术全面发展。应用混沌理论来控制噪声源线谱成分,首先要了解什么样的参数区域能使非线性隔振系统进入混沌运动、要知道如何判断系统是否已进入混沌状态、非线性隔振系统对线谱有多大的隔离能力等问题。本文基于上述问题做了一些基础性研究。内容主要包括非线性系统的基本性质,混沌产生的机理,两层非线性隔振系统的动力学特性分析,隔振效果评估等方面。较以往的研究,本系统考虑了基础的柔性,并且采用特征频率处线谱强度对系统隔振性能进行评估。
1 双层非线性隔振系统模型在传统的隔振理论分析具体问题时往往假定:被隔振的设备是无弹性的,理想化的,并且隔振器只是由简单理想的线性或非线性弹簧与理想化阻尼器并联而成,而且也将系统基础看成是质量趋于无穷的绝对刚体。导致高频区的隔振效果有所降低,在影响隔振效果的诸多因素中,基础的柔性是最重要的因素[3]。特别是对于大多为板壳结构的船体,其动力机械设备质量往往较大,与基础之间的动态耦合作用不能忽视,应将其基座视为具有一定机械阻抗的柔性基础。
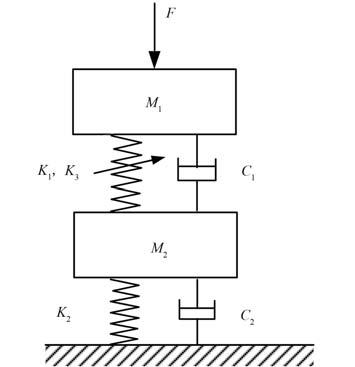
假设只考虑基于柔性基础的双层隔振系统垂直方向的振动传递,则可将系统简化为如下的两自由度模型,如图 1 所示。M1,M2 分别表示被隔振设备、基础的质量;X1,X2 分别表示为被隔振系统、基础的位移;假设基础的弹性支撑为线性,K2,C2 分别表示其刚度,阻尼系数;隔振材料具有非线性特征,K1,K3 分别表示刚度的 1 次项、3 次项系数;F 为加在隔振系统上的激励,假定
|
图 1 双层非线性隔振系统 Fig. 1 Double-layer nonlinear vibration isolation system |
根据所建模型可得系统运动微分方程为:
| $\left\{ \begin{array}{*{35}{l}} {{M}_{1}}{{{\ddot{X}}}_{1}}+{{C}_{1}}({{{\dot{X}}}_{1}}-{{{\dot{X}}}_{2}})+{{K}_{1}}({{X}_{1}}-{{X}_{2}})+ \\ {{K}_{3}}{{({{X}_{1}}-{{X}_{2}})}^{3}}={{F}_{1}}\text{cos}\Omega T+{{F}_{2}}, \\ {{M}_{2}}{{{\ddot{X}}}_{2}}+{{C}_{1}}({{{\dot{X}}}_{2}}-{{{\dot{X}}}_{1}})+{{K}_{1}}({{X}_{2}}-{{X}_{1}})+ \\ {{K}_{3}}{{({{X}_{2}}-{{X}_{1}})}^{3}}+{{C}_{2}}{{{\dot{X}}}_{2}}+{{K}_{2}}{{X}_{2}}=0. \\ \end{array} \right.$ | (1) |
令
| $\frac{\text{d}{{X}_{1}}}{\text{d}T}={{\omega }_{1n}}\sqrt{\frac{{{K}_{1}}}{{{K}_{3}}}}\frac{\text{d}{{x}_{1}}}{\text{d}t},\frac{\text{d}{{X}_{2}}}{\text{d}T}={{\omega }_{1n}}\sqrt{\frac{{{K}_{1}}}{{{K}_{3}}}}\frac{\text{d}{{x}_{2}}}{\text{d}t},$ | (2) |
| $\frac{{{{\rm d}^2}{X_1}}}{{{\rm d}{T^2}}} = {\omega ^2}_{1n}\sqrt {\frac{{{K_1}}}{{{K_3}}}} \frac{{{{\rm d}^2}{x_1}}}{{{\rm d}{t^2}}},\frac{{{{\rm d}^2}{X_2}}}{{{\rm d}{T^2}}} = {\omega ^2}_{1n}\sqrt {\frac{{{K_1}}}{{{K_3}}}} \frac{{{{\rm {\rm d}}^2}{x_2}}}{{{\rm d}{t^2}}}\text{。}$ | (3) |
将式(2)和式(3)代入式(1)可得到:
| $\left\{ \begin{array}{*{35}{l}} {{{\ddot{x}}}_{1}}+{{\xi }_{1}}({{{\dot{x}}}_{1}}-{{{\dot{x}}}_{2}})+({{x}_{1}}-{{x}_{2}})+ \\ {{({{x}_{1}}-{{x}_{2}})}^{3}}={{f}_{1}}\text{cos}\omega t+{{f}_{2}}, \\ {{{\ddot{x}}}_{2}}+\mu {{\xi }_{1}}({{{\dot{x}}}_{2}}-{{{\dot{x}}}_{1}})+\mu ({{x}_{2}}-{{x}_{1}})+ \\ \mu {{({{x}_{2}}-{{x}_{1}})}^{3}}+{{\xi }_{2}}{{{\dot{x}}}_{2}}+\mu \beta {{x}_{2}}=0. \\ \end{array} \right.$ | (4) |
式中:
| $\begin{array}{*{35}{l}} {{\xi }_{1}}=\frac{{{C}_{2}}}{\sqrt{{{M}_{1}}{{K}_{1}}}},\mu =\frac{{{M}_{1}}}{{{M}_{2}}},\beta =\frac{{{K}_{2}}}{{{K}_{1}}}, \\ {{\xi }_{2}}=\mu \frac{{{C}_{2}}}{{{C}_{1}}}{{\xi }_{1}},{{f}_{1}}=\sqrt{\frac{{{K}_{3}}}{K_{1}^{3}}}{{F}_{1}},\omega =\frac{\Omega }{{{\omega }_{1n}}}. \\ \end{array}$ | (5) |
将方程(4)改写成如下方程组形式:
| $\left\{ \begin{array}{*{35}{l}} {{{\dot{x}}}_{1}}={{y}_{1}}, \\ {{{\dot{y}}}_{1}}={{f}_{1}}\text{cos}\omega t+{{f}_{2}}-{{\xi }_{1}}({{y}_{1}}-{{y}_{2}})- \\ \quad \ \ \ ({{x}_{1}}-{{x}_{2}})-{{({{x}_{1}}-{{x}_{2}})}^{3}}, \\ {{{\dot{x}}}_{2}}={{y}_{2}}, \\ {{{\dot{y}}}_{2}}=-\mu {{\xi }_{1}}({{y}_{2}}-{{y}_{1}})-\mu ({{x}_{2}}-{{x}_{1}})- \\ \quad \ \ \ \mu {{({{x}_{2}}-{{x}_{1}})}^{3}}-{{\xi }_{2}}{{y}_{2}}-\mu \beta {{x}_{2}}. \\ \end{array} \right.$ | (6) |
令:
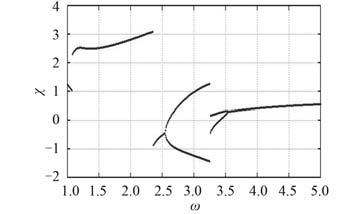
当 f1 = 4 时,被隔振设备响应随激励频率 ω 变化的分岔情况如图 2 所示。当
|
图 2 f1 = 4 时系统响应随激励频率变化的分岔图 Fig. 2 Bifurcation diagram in term of excitation frequency when f1 = 4 |
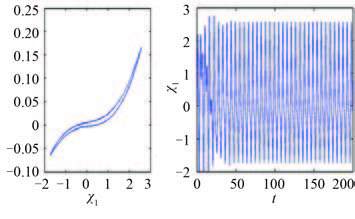
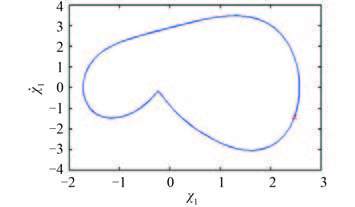
当 ω = 1.14 时,系统的轴心轨迹图及时域波形图如图 3 所示。从轴心轨迹图中可看出,隔振系统呈现非线性特征,且时域波形图为稳定的周期信号,系统响应相图如图 4 所示,在相图中相轨迹转一圈就发生了闭合,且相轨迹上只存在一个 Poincaré 截点,非常直观地看出此时系统只有一个稳定的周期解。
|
图 3 ω = 1.14 时系统响应的轴心轨迹图和时域波形图 Fig. 3 Orbit and time-history diagrams of the system response at ω = 1.14 |
|
图 4 ω = 1.14 周期 1 运动时系统响应相图 Fig. 4 Phase plot of P-1 motion when ω = 1.14 |
当 ω = 1.07 时,系统出现了第 1 次跳跃现象,系统响应由一个稳定的周期 1 运动突变为另一个稳定的周期 1 运动,当 ω = 2.36 时,系统又出现了第 2 次跳跃现象。
当 ω = 2.54 时,系统出现了第 1 次倍周期分岔过程,系统响应由一个稳定的周期 1 运动倍周期分岔为一个稳定的周期 2 运动,在 ω = 3.55 之前,系统一直维持周期 2 运动,在此频率范围内,当 ω = 3.26 时,系统出现了第 3 次跳跃现象,此次跳跃是由一个稳定周期 2 运动变化为另外一个稳定的周期 2 运动。
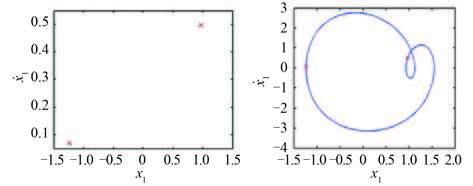
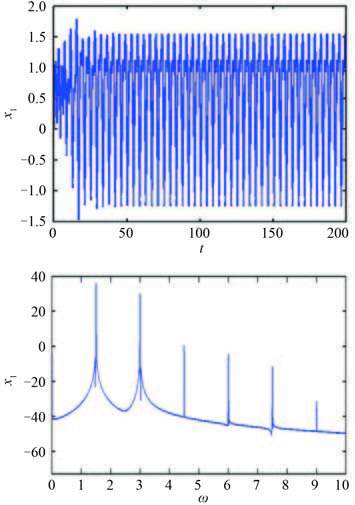
当 ω = 3 时,系统响应相图、Poincaré 截面图、时域图及功率谱图如图 5 和图 6 所示。在相图中,相轨迹旋转 2 圈后才发生闭合,在 Poincaré 截面图可以清楚地看到 2 个截点,由此判断系统响应为周期 2 运动,并且在功率谱图上可以看到此时系统出现了很强烈的 1/2 次谐波分量,即经过一次倍周期分岔过程后,系统响应在 1/2 倍激励频率处出现了很强的线谱。
|
图 5 ω = 3 周期 2 运动时系统响应的相图、Poincaré 截面图 Fig. 5 Phase plot and Poincaré map of P-2 motion when ω = 3 |
|
图 6 ω = 3 周期 2 运动时系统响应的时域图、功率谱图 Fig. 6 Time-history and amplitude spectrum diagram of P-2 motion when ω = 3 |
当 ω = 3.55 时,此时系统再次出现分岔现象,但此次分岔过程是周期 2 运动变为周期 1 运动,系统响应只在激励频率处出现强烈的线谱。经过此次倍周期分岔过程之后,系统一直保持周期 1 运动。
但在整个 ω 范围内,由于激励幅值 f1 较小,并未观察到混沌现象。
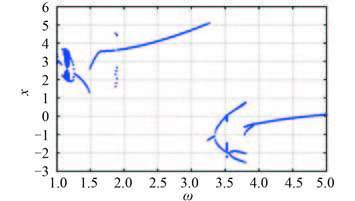
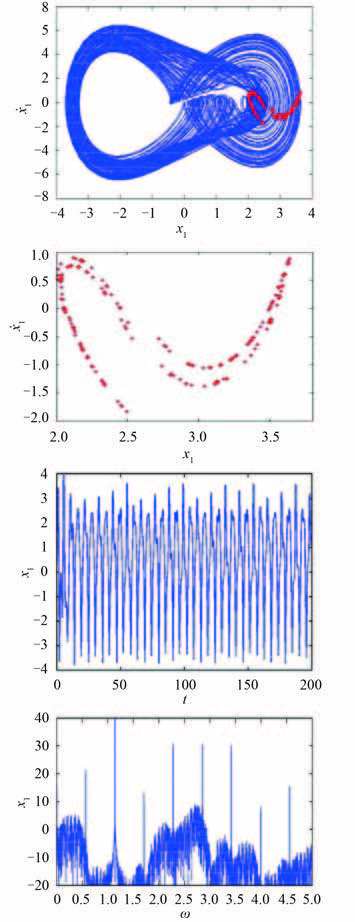
当 f1 = 12 时,被隔振系统响应随激励频率 ω 的分岔情况如图 7 所示。与 f1 = 4 时的分岔图相比,系统响应不仅多次出现了倍周期分岔过程,而且还出现了混沌现象。由图 7 可知,在 ω = 1.14 附近,系统进入混沌状态。此时 Poincaré 截面上也存在明显的混沌吸引子,时域波形图呈现无规则的现象,通过计算功率谱,观察到除了出现超谐波之外,在 ω = 0.57 处还出现了较强 1/2 次谐波,并且还存在连续幅值较小的谐波分量,如图 8 所示。并且可以观察到,每经过一次倍周期分岔,新出现的谱线强度会明显降低,这对降低辐射噪声非常有利。由此可以得出,该隔振系统在 ω = 1.14 附近存在着倍周期分岔和非常复杂的混沌运动。在设计非线性隔振器时,就是要在外界激励幅值基本不变的情况下,想方设法保证隔振系统的固有频率使整个隔振系统处于混沌状态,这样辐射噪声中的线谱成分将会得到很好的隔离。
|
图 7 f1 = 12 时系统响应随激励频率变化的分岔图 Fig. 7 Bifurcation diagram in term of excitation frequency when f1 = 12 |
|
图 8 ω = 1.14 混沌状态时系统响应的相图、Poincaré 图、时域图及功率谱图 Fig. 8 Phase, Poincaré map, time-history and amplitude spectrum diagrams of system response at different exciation frequency |
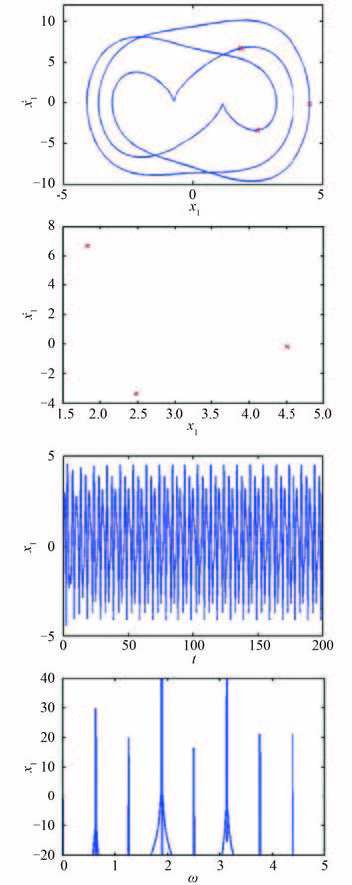
当 ω > 1.17 时,系统响应由混沌运动→周期 8→周期 4→周期 2 不断演变,当 ω = 1.26 时,系统再次进入周期 1 运动。在 1.87 < ω < 1.89 的频率范围内系统响应还出现了短暂的周期 3 运动。当 ω = 1.88 时,在 Poincaré 截面上可以明显地观察到 3 个孤立的截点,如图 9 所示。随着激励频率继续增大,在 ω = 3.24 附近,系统响应出现了跳跃现象,随即出现了倍周期分岔过程,其演变过程为周期 1→周期 2→周期 4→周期 2运动,当 ω = 3.94 时,系统又进入了周期 1 运动。
|
图 9 ω = 1.88 周期 3 运动时系统响应的相图、Poincaré 图、时域图及功率谱图 Fig. 9 Phase, Poincaré map, time-history and amplitude spectrum diagrams of system response of P-3 motion when ω = 1.88 |
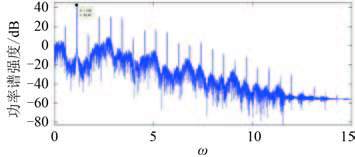
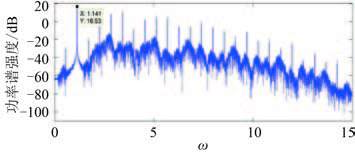
对图 7 中优势频率 ω = 1.14 处隔振性能进行研究。图 10 为被隔振设备的功率谱图,最大为 42.47 dB,图 11 为通过隔振器后基础响应的功率谱强度,最大为 16.53 dB,线谱强度共下降了 42.47 - 16.53 = 25.94 dB。因此可以看出系统处于混沌状态对优势频率处线谱的隔离效果明显。
|
图 10 ω = 1.14 时被隔振设备响应的功率谱图 Fig. 10 Amplitude spectrum of the machinery when ω = 1.14 |
|
图 11 ω = 1.14 时基础响应的功率谱图 Fig. 11 Amplitude spectrum of the foundation when ω = 1.14 |
以上分析表明,双层非线性隔振系统在外界激励幅值一定的条件下,随激励幅值的变化呈现出非常复杂的动力学特性,激励幅值越大,系统更容易出现混沌状态,并且在混沌状态时,能有效隔离机械设备辐射噪声中的线谱成分,因而非线性系统运用到机械设备隔振装置中非常有效可行。
| [1] |
谢向荣, 朱石坚. 船舶动力机械双层混合隔振系统非线性动力学特性研究[J]. 振动与冲击 , 2010, 29 (3) :174–177.
XIE Xiang-rong, ZHU Shi-jian. Nonlinear dynamics of two-stages hybrid isolation system of power machinery on ships[J]. Journal of Vibration and Shock , 2010, 29 (3) :174–177. |
| [2] | CREDE C E. Vibration and shock isolation[M]. New York: John Wiley & Sons, 1951 . |
| [3] |
朱石坚, 楼京俊, 何其伟, 等.
振动理论与隔振技术[M]. 北京: 国防工业出版社, 2006 .
ZHU Shi-jian, LOU Jing-jun, HE Qi-wei, et al. Vibration theory and vibration isolation[M]. Beijing: National Defense Industry Press, 2006 . |
| [4] |
姜荣俊.控制混沌技术在隔振系统中的应用研究[D].武汉:海军工程大学, 2002.
JIANG Rong-jun. Application of chaos control on vibration isolation system[D]. Wuhan:Naval University of Engineering, 2002. |
| [5] |
刘树勇. 混沌振动的识别研究[D]. 武汉:海军工程大学, 2003.
LIU Shu-yong. Research on chaos identification[D]. Wuhan:Naval University of Engineering, 2003. |
| [6] |
姜荣俊, 朱石坚, 何琳. 混沌振动在水声对抗中的应用前景[J]. 非线性动力学学报 , 2001, 8 (1) :15–18.
JIANG Rong-jun, ZHU Shi-jian, HE Lin. Prospect of application of chaotic vibration in the waterborne-noise confrontation[J]. Journal of Nonlinear Dynamics in Science and Technology , 2001, 8 (1) :15–18. |
| [7] |
俞翔, 刘树勇, 朱石坚. 非线性隔振系统混沌特性实验研究[J]. 噪声与振动控制 , 2003, 23 (4) :9–11.
YU Xiang, LIU Shu-yong, ZHU Shi-jian. Experimental research on the chaotic characteristics of nonlinear vibration isolation system[J]. Noise and Vibration Control , 2003, 23 (4) :9–11. |
| [8] | LOU J J, ZHU S J, HE L, et al. Application of chaos method to line spectra reduction[J]. Journal of Sound and Vibration , 2005, 286 (3) :645–652. DOI:10.1016/j.jsv.2004.12.018 |
| [9] |
欧阳清.混沌振动与振动控制研究[D].武汉:海军工程大学, 2001.
OUYANG Qing. Study on chaos of vibration and vibration control[D]. Wuhan:Naval University of Engineering, 2001. |
 2016, Vol. 38
2016, Vol. 38
