快速傅里叶变换(FFT)出现以来,人们提出了多种以 FFT 算法为基础的数字信号处理方法。其中,级联 FFT、扫频窄带分析法、复调制 Zoom FFT 法、直接抽取法等都是能够进行频率细化的 FFT 算法[1]。在舰船电子信息系统中,FFT 作为基本的信号处理算法,在雷达、声呐、导航、电子对抗等电子装备中大量使用,是基本的时频信号处理工具。FFT 运算作为主要的信号处理工具通常占据了大量的信号处理硬件资源。级联 FFT 通过将大序列数据分成两级短序列数据进行 FFT 处理的方式大大减轻了硬件上实现大序列 FFT 的压力。但是,分段处理的方法带来了能量泄漏和频率镜像现象的出现。文献[2]研究了 FFT 和级联 FFT 计算结果之间的差异,并对正弦信号的分析结果给出了一种补偿方法,但在采用级联 FFT 对非正弦的一般信号进行处理时,该文献描述的补偿方法受到一定的限制。文献[3]提出了一种改进的级联 FFT 算法,通过对数据的加窗和对输出结果进行相邻段之间的平均和修正来减小误差带来的影响,但仍然没有能够完全避免能量泄漏和处理数据量增大的现象。
1 基本级联 FFT 的算法原理级联 FFT 算法的理论基础是通过将数据分段,通过两级长度较短的 FFT 运算来实现一个序列全长度的 FFT 结果,使得频谱分辨能力,从而减少硬件资源上的消耗。
M × N 点序列信号 x(n + mN),n = 0,1,2,…,N-1;m = 0,1,2,…,M-1,利用级联 FFT 进行处理可以表示为 2 级 FFT 串联的变现形式。通过矩阵化,一维序列可以表示为二维 M × N 矩阵的形式,对于 N 点表示的数据进行 FFT 运算可以表示为:
| ${{X}_{m}}(q)=\sum\limits_{n=0}^{N-1}{x(n+mN){{e}^{-j2\pi nq/N}}}=\text{FF}{{\text{T}}_{n}}[x(n+mN)].$ | (1) |
对第一次 FFT 之后,相同频率点上但不同段上的 M 点数据做 FFT 分析,可以表示为:
| $\begin{align} & X'(p+qM)=\text{FF}{{\text{T}}_{m}}\{\text{FF}{{\text{T}}_{n}}[x(n+mN)]\}= \\ & \sum\limits_{m=0}^{M-1}{{{e}^{-j2\pi mp/M}}\left( \sum\limits_{n=0}^{N-1}{x(n+mN){{e}^{-j2\pi nq/N}}} \right)}, \\ \end{align}$ | (2) |
其中 q = 0,1,2,…,N-1;p = 0,1,2,…,M-1,这样就得到了基本级联 FFT 算法的结果。
对一个长度为 M × N 的时间序列信号 x(n + mN),n = 0,1,2,…,N-1;m = 0,1,2,…,M-1,进行离散傅里叶变换之后得到的频谱为:
| $X(p+qM)=\sum\limits_{n=0}^{N-1}{\sum\limits_{m=0}^{M-1}{x(n+mN){{e}^{-j2\pi \left( p+qM \right)\left( n+mN \right)/MN}}}},$ | (3) |
其中 q = 0,1,2,…,N-1;p = 0,1,2,…,M-1考虑因子
| $\begin{array}{*{35}{l}} {{X}_{1}}(p+qM)=\sum\limits_{m=0}^{M-1}{{{e}^{-j2\pi mp/M}}\left( \sum\limits_{n=0}^{N-1}{x(n+mN){{e}^{-j2\pi nq/N}}} \right)}= \\ \text{FF}{{\text{T}}_{m}}\{\text{FF}{{\text{T}}_{n}}[x(n+mN)]\}.\quad \quad \quad \quad \quad \\ \end{array}$ | (4) |
可以看到,式(4)与式(2)的表现形式相同。这就表明,级联 FFT 算法是在
在上面的数学运算过程中,假定交叉项因子等于 1,而实际上该因子是一个变量。根据推导,交叉项因子式以下面的形式存在并耦合到两级运算当中,即
| ${{e}^{-j2\pi n\left( q+p/M \right)/N}}.$ | (5) |
该交叉项因子两级变量 n 和 p 的函数。在 p ≠ 0 的情况下,该交叉项因子的结果不等于 1。如果不对第一段 FFT 运算的结果进行修正,将会出现误差,并带来相邻频点上能量的扩散。通过分析和仿真计算,在 p/M ≈ 1/2 附近时,将产生最大误差,能量的泄漏大约在 50% 左右。
为解决粗频谱分析时的能量泄漏,往往采用对第一次分段的数据进行重叠,并通过加窗降旁瓣和对最终的输出结果进行幅度矫正才能达到较满意的效果[1-2]。但是,为达到较好处理效果的 50% 以上的重叠比将会大大增加处理的运算量以及复杂程度。
2.2 基于交叉项补偿的级联 FFT 算法根据分析发现,对于误差项的补偿,将会大大影响处理的结果。考虑到 FFT 预算的线性特性,矩阵化后数据的两维傅里叶变化的顺序并不影响最终的运算结果。因此,在将两维变换顺序调整之后,可以得到:
| $\begin{array}{*{35}{l}} {{X}_{1}}(p+qM)=\sum\limits_{n=0}^{N-1}{{{e}^{-j2\pi nq/N}}\sum\limits_{m=0}^{M-1}{x(n+mN){{e}^{-j2\pi mp/M}}}}= \\ \text{FF}{{\text{T}}_{n}}\{\text{FF}{{\text{T}}_{m}}[x(n+mN)]\}. \\ \end{array}$ | (6) |
这时再考虑
| $\begin{align} & X(p+qM)=\sum\limits_{n=0}^{N-1}{\sum\limits_{m=0}^{M-1}{x(n+mN){{e}^{-j2\pi n\left( q+p/M \right)/N}}}}\times {{e}^{-j2\pi mp/M}}= \\ & \sum\limits_{n=0}^{N-1}{{{e}^{-j2\pi n\left( q+p/M \right)/N}}\sum\limits_{m=0}^{M-1}{x(n+mN){{e}^{-j2\pi mp/M}}}}= \\ & \sum\limits_{n=0}^{N-1}{{{e}^{-j2\pi nq/N}}{{e}^{-j2\pi np/MN}}X(p,n)}. \\ \end{align}$ | (7) |
其中 X(p,n)为沿 m 方向进行 FFT 计算的结果。
如果从 z 变换的角度来理解 FFT,FFT 实际上是从单位圆零相角开始,角度等分之后得到的 z 变换的数值。根据式(7)的结果,第 2 次变换时的 FFT 核函数变为
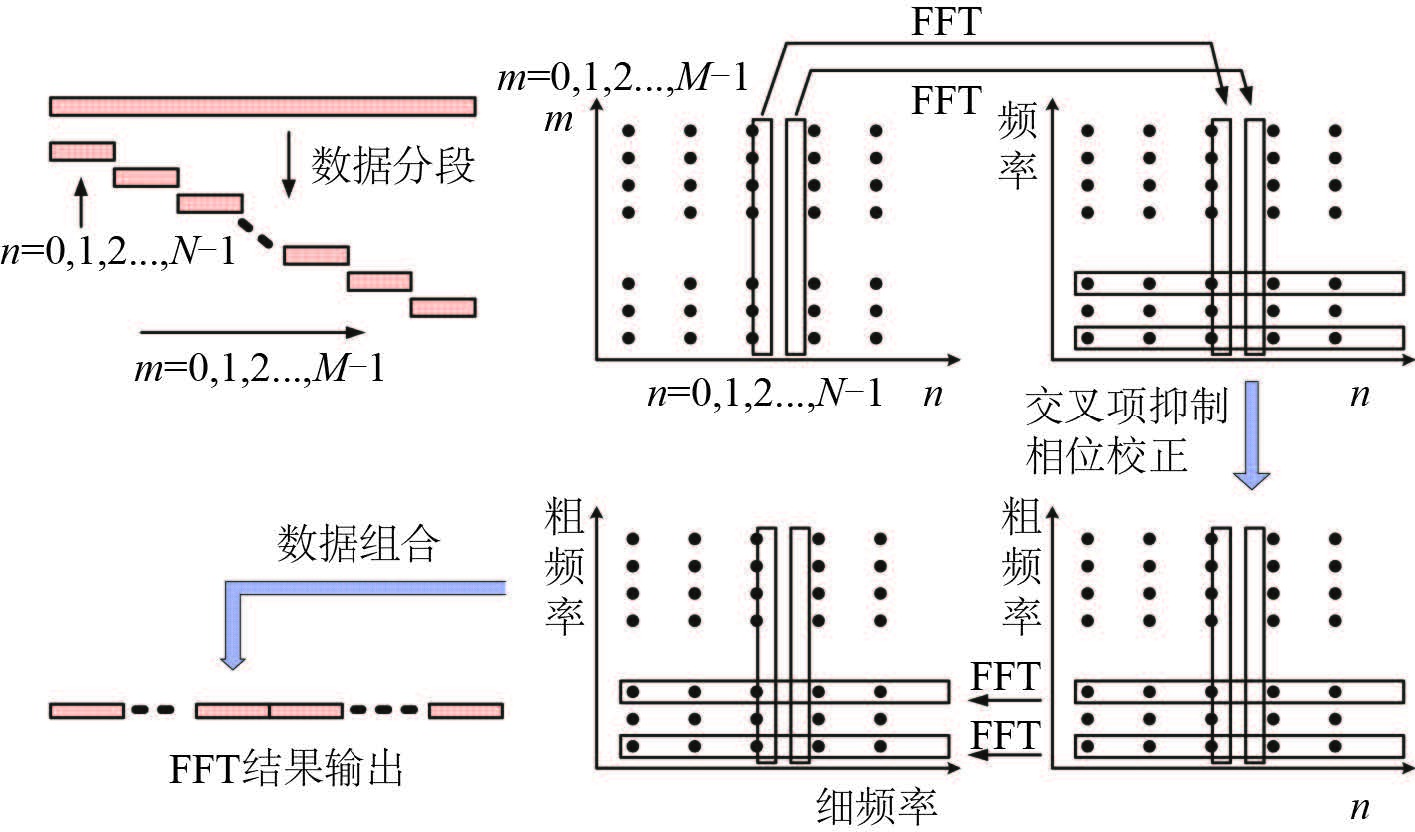
|
图 1 基于交叉项补偿的 FFT 算法示意图 Fig. 1 Diagram of FFT algorithm based on intersection factor compensation |
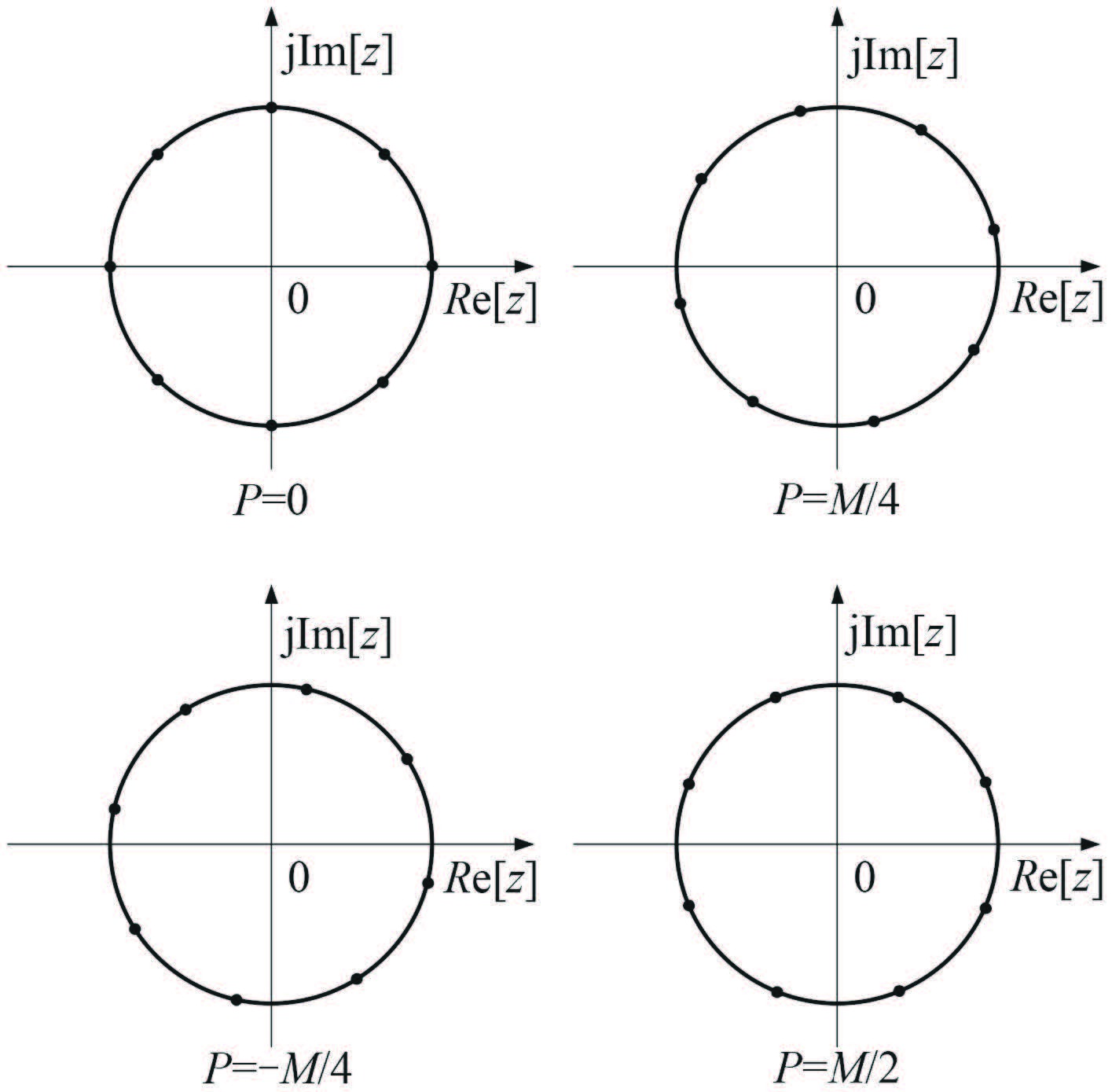
|
图 2 交叉项影响相角示意图 Fig. 2 Diagram of influence of intersection factor to the phase angle |
可以看出,改进算法采用了与传统算法不同的矩阵运算顺序,同时增加了交叉项抑制和相位补偿运算。新算法不需要对分段后的数据取重叠,只是通过复乘的操作就实现了交叉项抑制和补偿,运算量相比传统方法将会大大减小,同时还能得到较好的处理结果。
3 算法仿真及性能分析根据上文的分析,给出基于交叉项补偿的级联 FFT 算法的实现流程如图 2 所示。

|
图 3 基于交叉项补偿的级联 FFT 处理流程图 Fig. 3 Flow chart of Cascade FFT algorithm based on intersection factor compensation |
根据逆序级联 FFT 算法的步骤,下面给出对一个线性调频信号进行频谱分析的实例,并对实现时的运算量大小进行分析。仿真所用的线性调频信号的带宽为 80 Hz,信号持续时间为 5 s,采样频率为 200 Hz,采用的分段方式为 N = 50,M = 20 和 N = 10,M = 100。
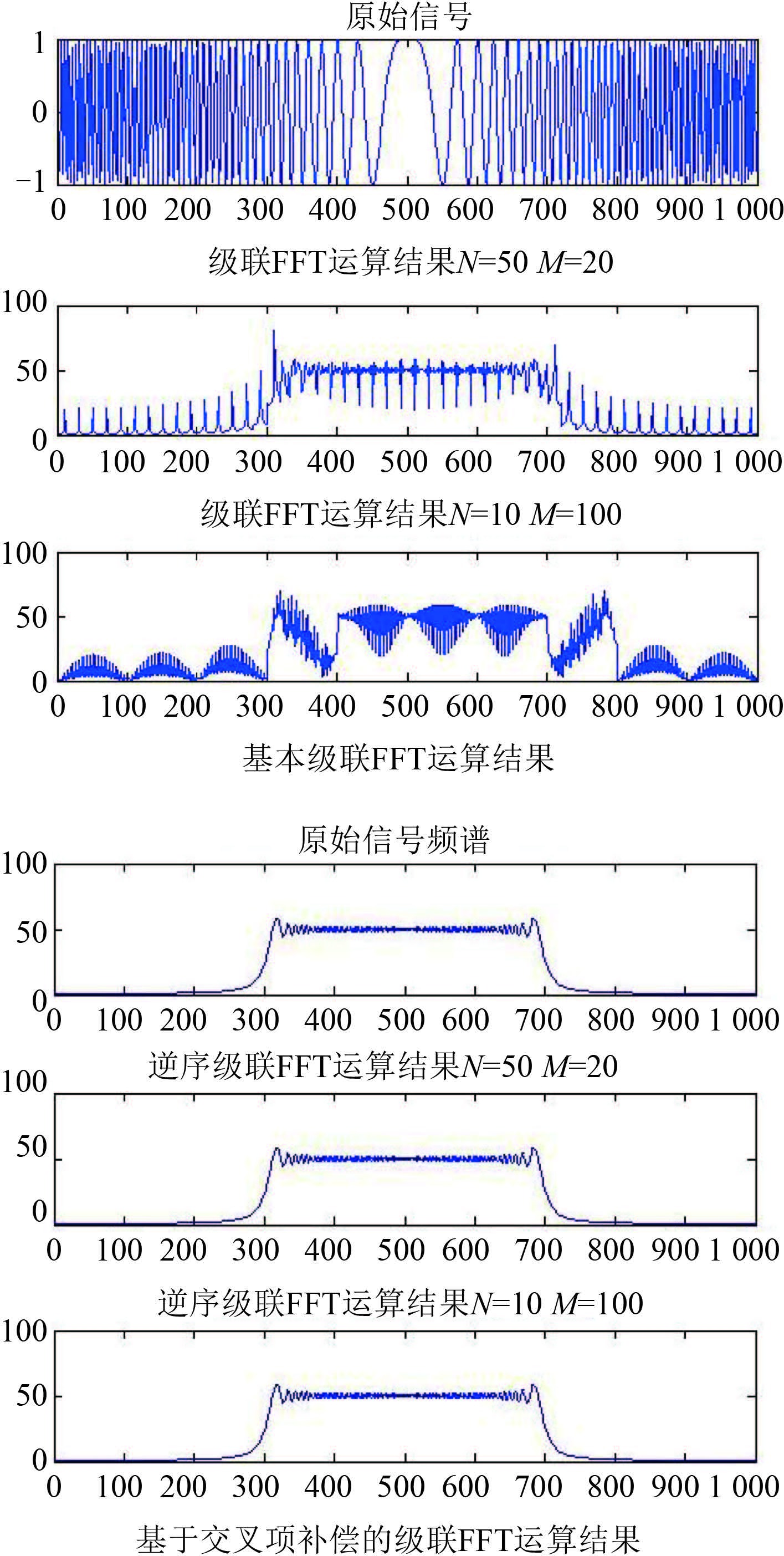
|
图 4 新算法进行处理后的频谱分析对比 Fig. 4 Spectrum comparison of new algorithm |
表 1 给出了基本算法在不取重叠、50% 重叠的计算结果和采用基于交叉项补偿的级联 FFT 算法进行运算时的运算量对比。
|
|
表 1 两种算法的运算量比较 Tab.1 Calculation amount comparison of two algorithm |
从分析结果可看出,通过增加一次复乘操作来进行交叉项补偿,实现了 2 级 FFT 运算之间分数分量的影响,并得到与一次全长度序列 FFT 完全相同的运算结果。相对传统算法采用大重叠比实现栅瓣抑制的方法,新算法每次进行 FFT 运算的长度可大大缩短,同时以较小的复乘运算换来了实现长序列 FFT 频谱分析的问题,这对于雷达、声呐、电子对抗等大量需要大数据量 FFT 运算的领域很有实际意义。
4 结语本文在分析传统的级联 FFT 算法的基础上,提出一种新的基于交叉项补偿的级联 FFT 算法。该算法首先对输入时间序列的数据进行抽样,然后对抽样后数组内的数据进行 FFT 运算处理,然后进行交叉项的补偿,再对 FFT 之后不同数组间相同位置上的数据进行第 2 次 FFT 处理,从而达到一次 FFT 运算能够得到的效果。该算法能够有效避免栅瓣效应和能量泄漏现象给级联 FFT 运算带来的影响,从而实现用短序列 FFT 运算来进行长序列 FFT 运算的结果。同传统的级联 FFT 算法相比,改进的算法能够避免了原有算法的不足,同时在运算量上也避免了由于不同数据段之间重叠比过高所带来的运算量的增加。
| [1] | PERRY R P, KAISER H W. Digital step transform approach to airborne radar processing[C]//Proceedings of IEEE National Aerospace and Electronics Conference. New York:IEEE, 1973:280-287. |
| [2] | YIP P C Y. Some aspects of the Zoom transform[J]. IEEE Transactions on Computers , 1976, C-25 (3) :287–296. DOI:10.1109/TC.1976.5009255 |
| [3] | FJELL P O, LUNDE E B. A modified cascade fast Fourier transform in a spectrum analysing system[C]//Proceedings of IEEE international conference on ICASSP '77 acoustics, speech, and signal processing. Hartford, CT, USA:IEEE, 1997, (2):873-876. |
| [4] | HOYER E A, STORK R F. The Zoom FFT using complex modulation[C]//Proceedings of IEEE international conference on ICASSP '77 acoustics, speech, and signal processing. Hartford, CT, USA:IEEE, 1977, (2):78-81. |
| [5] | WU K H, VANT M R. Extensions to the step transform SAR processing technique[J]. IEEE Transactions on Aerospace and Electronic Systems , 1985, AES-21 (3) :338–344. DOI:10.1109/TAES.1985.310563 |
| [6] | MCGOEY-SMITH A D, VANT M R. Modification of the SAR Step Transform algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems , 1992, 28 (3) :666–674. DOI:10.1109/7.256289 |
| [7] | MOREIRA A. Real-time Synthetic aperture radar (SAR) processing with a new subaperture approach[J]. IEEE Transactions on Geoscience and Remote Sensing , 1992, 30 (4) :714–722. DOI:10.1109/36.158865 |
| [8] | SUN X B, YEO T S, ZHANG C B, et al. Time-varying step-transform algorithm for high squint SAR imaging[J]. IEEE Transactions on Geoscience and Remote Sensing , 1999, 37 (6) :2668–2677. DOI:10.1109/36.803414 |
| [9] | YEO T S, TAN N L, ZHANG C B, et al. A new subaperture approach to high squint SAR processing[J]. IEEE Transactions on Geoscience and Remote Sensing , 2001, 39 (5) :954–968. DOI:10.1109/36.921413 |
 2016, Vol. 38
2016, Vol. 38
