半潜式平台经历了从第一代半潜式平台到第六代半潜式平台的发展[1],已经从布局不合理、低自动化发展到了如今的合理布局、自动化程度高的特点。与其他海洋平台相比,半潜式平台具有适应工作水深广、抗风浪能力强、甲板面积和装载量大、转移安装方便等特点[2],一直得到广泛应用。半潜式平台通常由下浮体、撑杆、上部平台、立柱及重要节点组成[3]。海洋平台在作业时,总会遇到风、浪、流的联合作用,从而产生六自由度的运动[4],甚至引起系泊线断裂,严重影响平台作业。因此,国内外很多学者都对半潜式平台运动响应做了研究:张威等[5]对比了频域与时域 2 种方法预报半潜式平台运动响应结果的异同。刘应中等[6]采用准定长时间域法分析了在风、浪、流联合作用下海上系泊系统的运动及动力特性。聂武等[7]叙述了用于细长杆件波浪载荷计算的 Morison 公式及用于大尺度构件的波浪载荷计算理论与方法。O.Yilmaz [8]应用频域和时域分析方法对半潜式平台运动响应进行了模拟分析。
本文模拟半潜式平台在频域和时域下的响应预报结果,分析频域与时域预报响应的优缺点,以及在平台设计建造不同阶段,如何选择合适的预报方法。在时域条件下对比分析在不同风、浪、流组合工况下平台升沉运动幅值,计算所设计的半潜式平台系泊线的拉力,并进行安全校核。
1 平台主尺度参数及水动力模型为研究频域和时域在海洋平台运动响应预报中的特点,选用 SSCV-H206 半潜式起重平台,作业水深 1 000 m,主尺度见表 1。
|
|
表 1 半潜式平台的主尺度列表 Tab.1 Principle dimensions of semi-submersible platform |
给定系泊缆数量及其导缆孔位置,共有 12 根系泊缆,12 根系泊缆位置如下:原点纵向位置在首部向后 64 m,横向位置在中间,垂向位置在船底。系泊缆数量及导缆孔位置如表 2 所示。
|
|
表 2 系泊缆数量及导缆孔位置 Tab.2 Numbers of mooring lines and fairlead position |
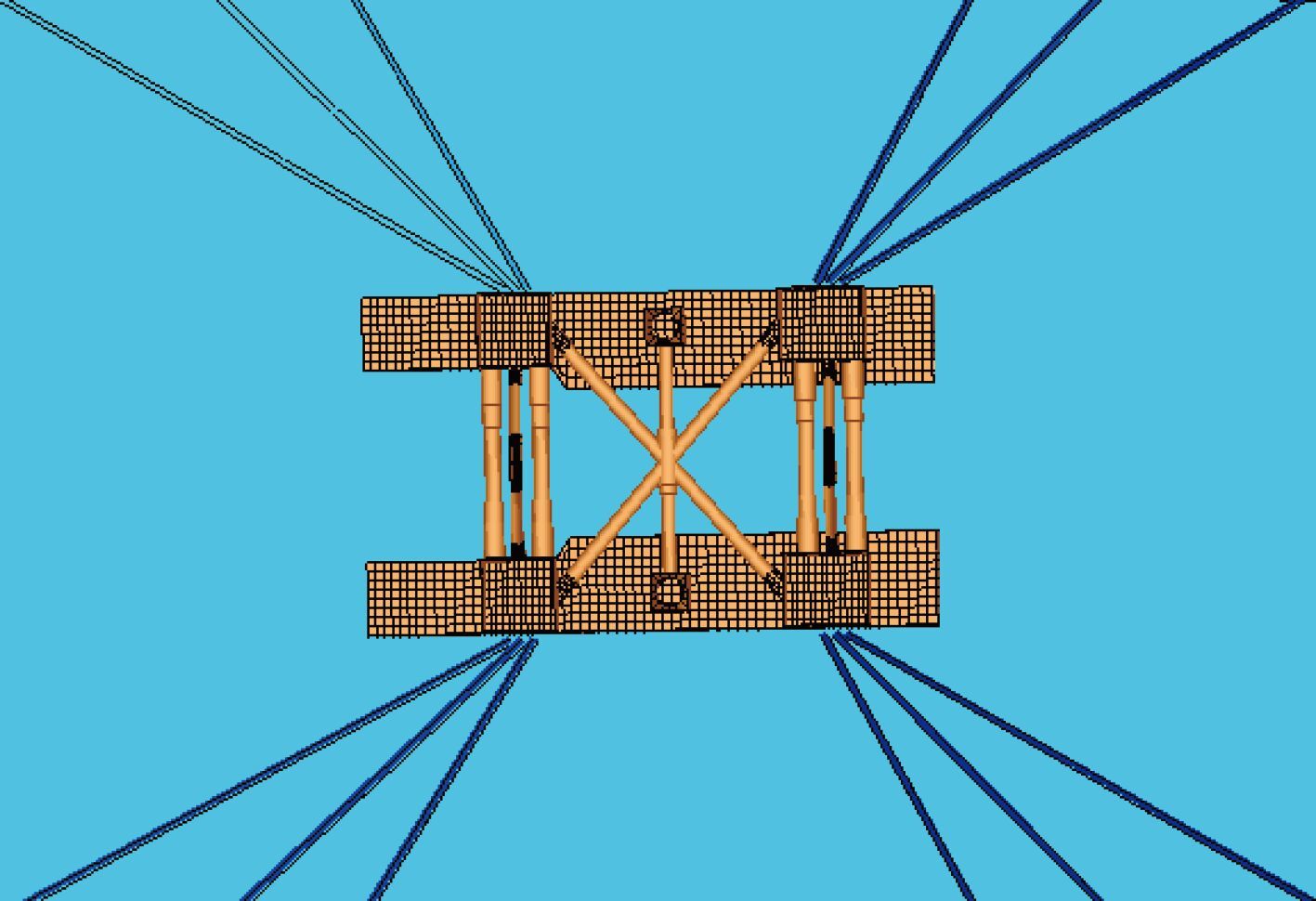
利用 Ansys 建立有限元模型后,导入到 AQWA 软件生成平台的水动力模型,如图 1 所示。
|
图 1 半潜式平台水动力模型 Fig. 1 Hydrdynamic model of semi-submersible platform |
频域计算是分析物体在波浪上运动响应的经典方法,通常用于计算无航速浮体在微幅规则波作用下的微幅运动,由于是微幅运动,因此可用线性理论进行求解。
在线性理论的假定下,浮体对于任一波浪成分的运动响应是这个成分波波幅的线性函数并且与它对其他波浪成分的响应独立无关,浮体的运动响应采用幅值响应算子 RAO 进行描述。幅值响应算子 RAO 是波浪波幅到平台各位置参数的传递函数,即
| $RAO={{\eta }_{i}}/\xi .$ | (1) |
式中:ηi 为平台运动第 i 个自由度的值;ξ 为某一频率波浪高度的幅值。
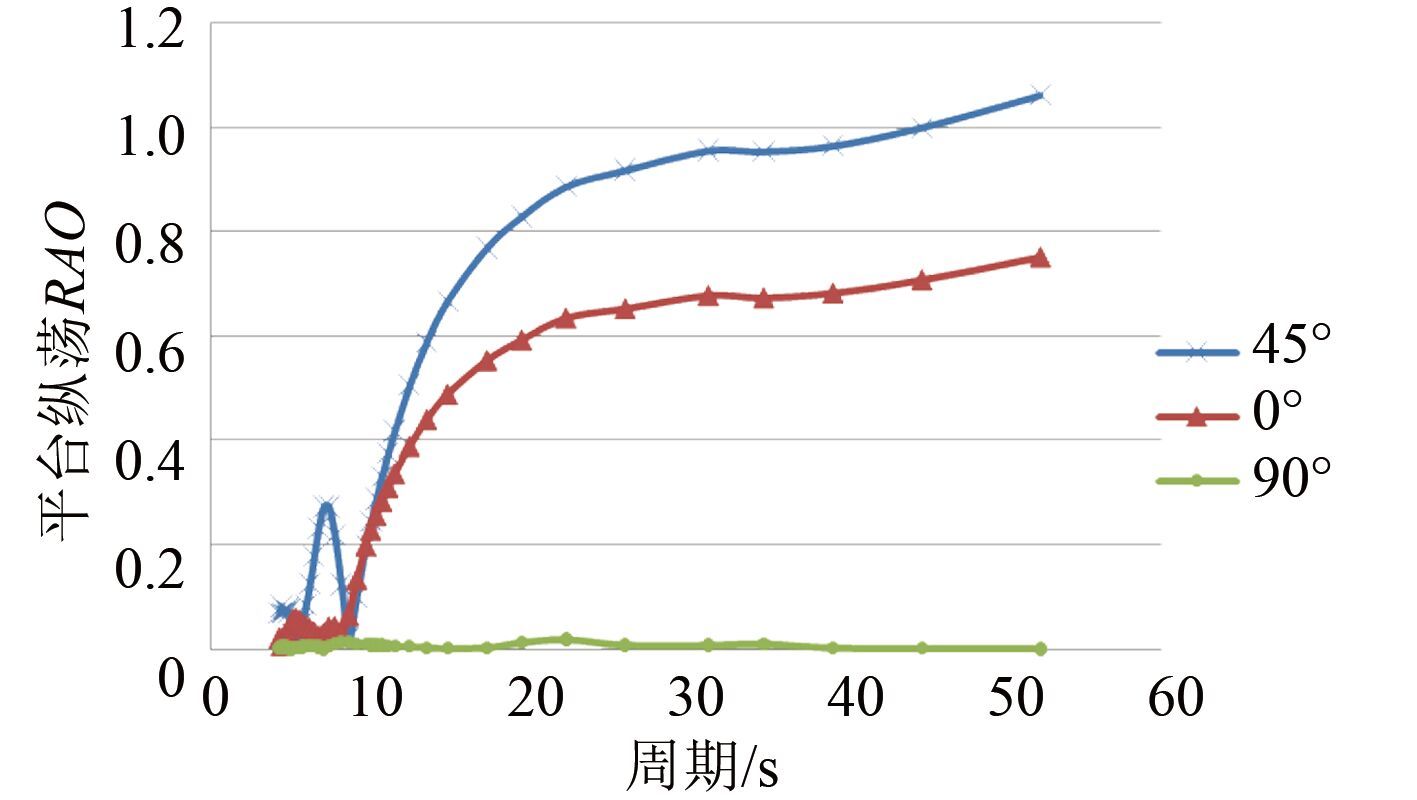
在建立平台水动力模型后,本文模拟了在未系泊情况下自由漂浮状态的 RAO。这里选取 0°,45°,90° 三个方向的浪向进行说明,给出平台纵荡、横荡及升沉的时历曲线。
|
图 2 平台纵荡 RAO Fig. 2 Sway RAO of semi-submersible platform |
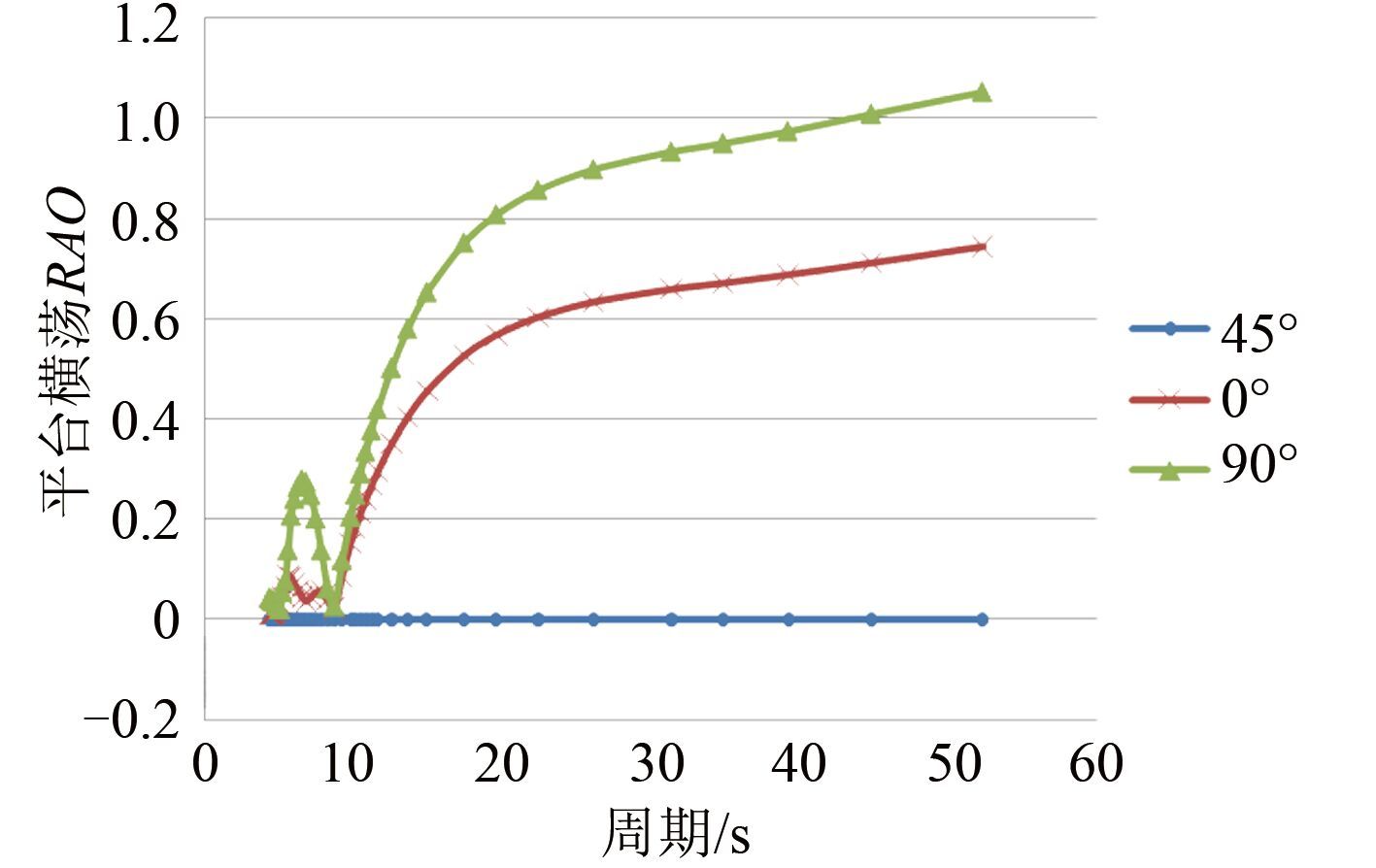
|
图 3 平台横荡 RAO Fig. 3 Surge RAO of semi-submersible platform |
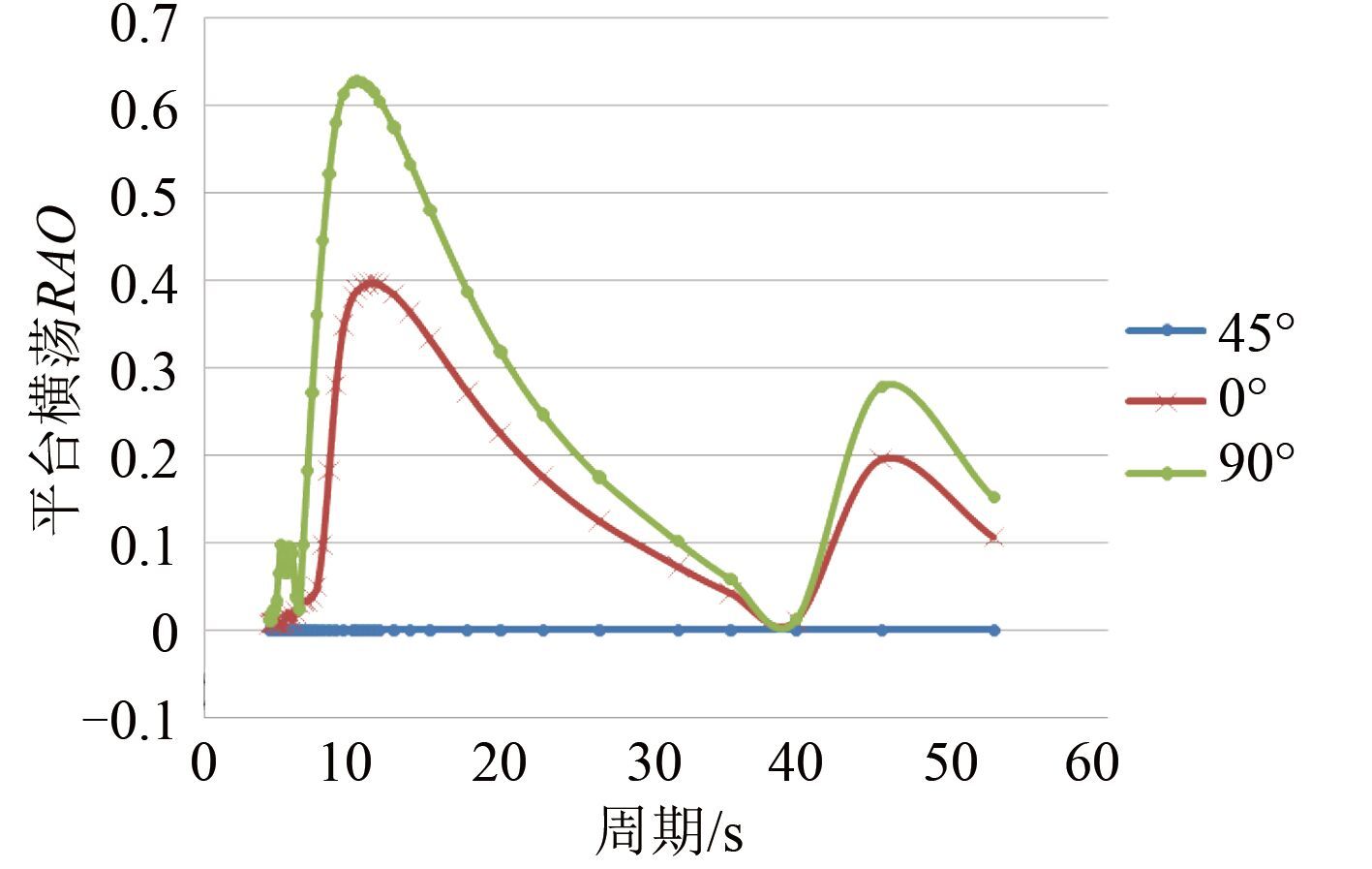
|
图 4 平台升沉 RAO Fig. 4 Heave RAO of semi-submersible platform |
当计算完半潜式平台运动响应 RAO 后,可采用拟静态方法预报半潜式平台运动响应,计算结果可看作频域响应预报结果。
3 时域分析时域分析可以模拟海洋结构物在一定时间范围内一定环境条件下的运动状态,并可以真实反映出其在海上的实际变化情况。对半潜式平台运动响应进行时域分析,首先要根据波浪谱随机生成波浪时历,然后在每一个时间步求解运动方程,在求解过程中,需要考虑平台与锚泊系统的耦合效应,并实时模拟平台的运动响应。本文对半潜式平台进行短期预报,在极端海况下 3 h 内对平台的运动响应及系泊系统响应情况进行描述。
3.1 海洋环境条件本文所分析的半潜式平台系泊系统采用十年一遇的风、浪、流组合作为设计工况,其风、浪、流的详细参数见表 3。
|
|
表 3 南海海况的风浪流参数 Tab.3 Parameters of wind, wave and flow in South China Sea |
对海洋结构物来说,其运动方程可写为:
| $\begin{align} & M\ddot{x}+C\dot{x}+{{D}_{1}}\dot{x}+{{D}_{2}}f(\dot{x})+K(x)x=q(t,x,\dot{x}), \\ & M=m+A(\omega )\text{,} \\ & A(\omega )={{A}_{\infty }}+a(\omega )\text{,} \\ & C(\omega )={{C}_{\infty }}+c(\omega )\text{,} \\ & {{C}_{\infty }}=C(\omega =\infty )\equiv 0. \\ \end{align}$ | (2) |
式中,M 为频域质量矩阵;m 为平台主体质量;A 为频域附加质量矩阵;C 为频域势流阻尼矩阵;D1 为线性阻尼矩阵;D2 为二阶阻尼矩阵;f 为矢量函数,每个单元由
通过提取半潜式平台 6 个自由度的时历曲线,对 6 个自由度的运动响应进行分析,获得平台在该海况下的运动情况,这里只给出浪、流、风分别为 0°,45°,30° 时平台纵荡和垂荡运动的响应曲线。时域运动响应结果见表 4。
|
|
表 4 半潜式平台时域运动响应预报结果 Tab.4 Time-domain motion response prediction result of semi-submersible platform |
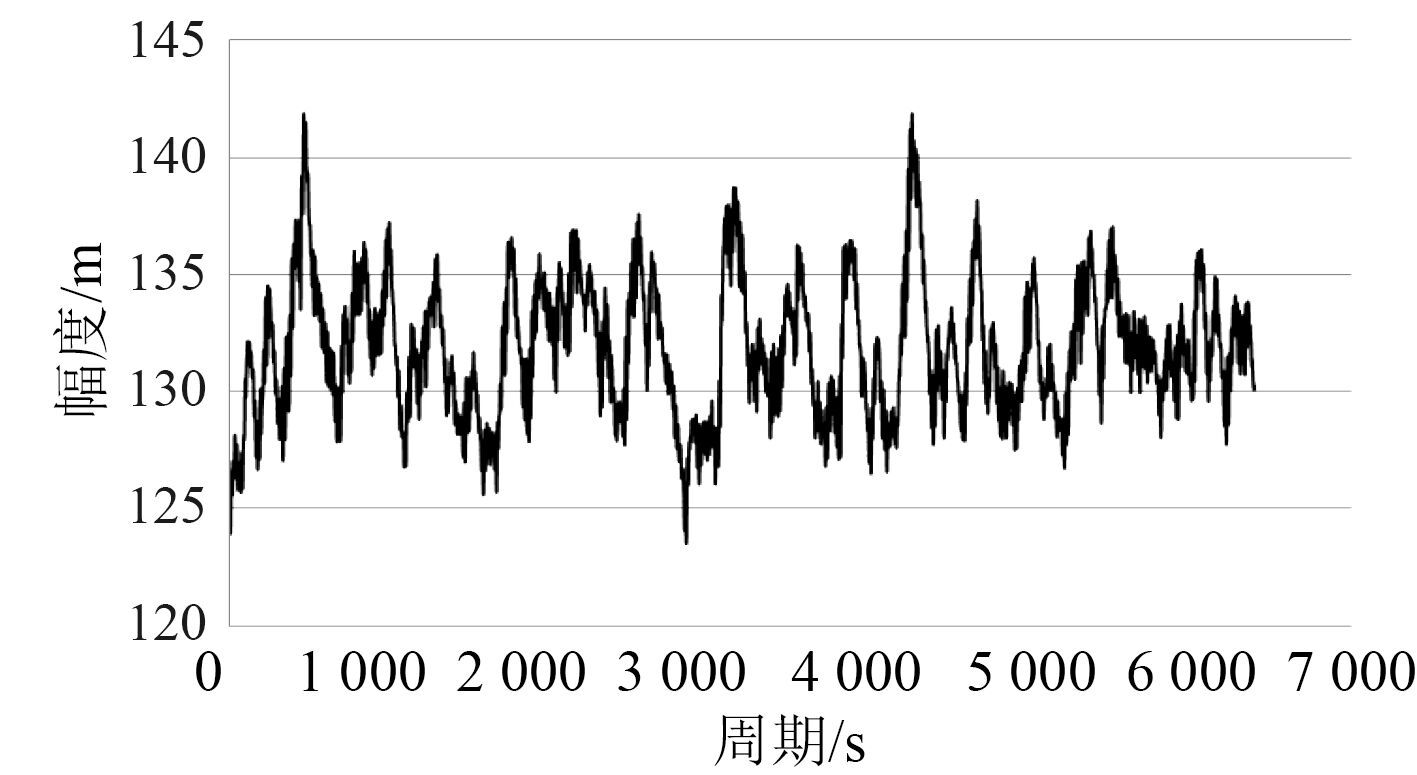
|
图 5 半潜式平台纵荡响应曲线 Fig. 5 Surge response curve of semi-submersible platform |
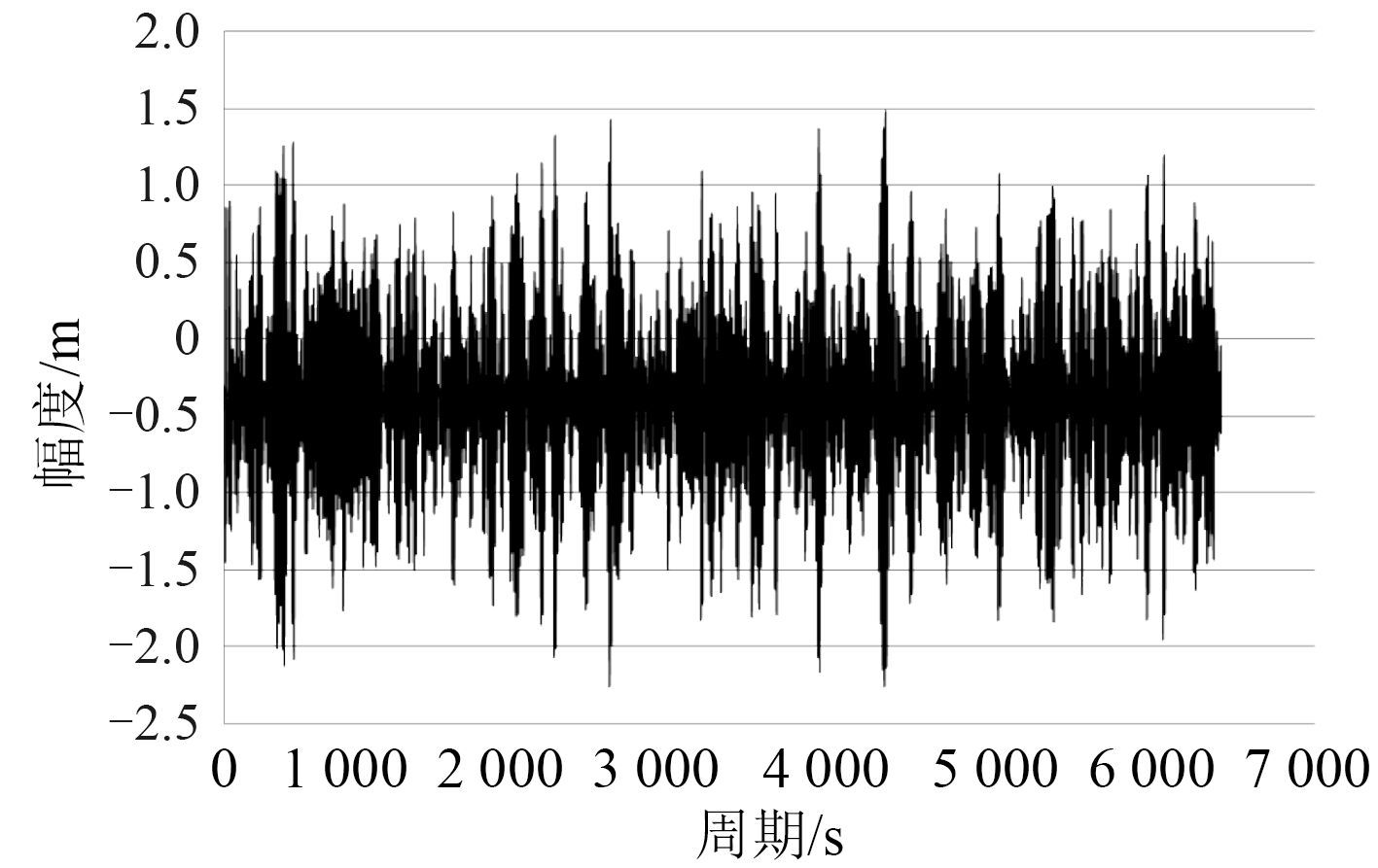
|
图 6 半潜式平台横荡响应曲线 Fig. 6 Sway response curve of semi-submersible platform |
为对比分析不同环境载荷对半潜式平台动力响应的影响,波浪谱的入射角取 0° 和 180° 两个方向。具体的风、浪、流组合如表 5 所示。
|
|
表 5 风、浪、流方向组合表 Tab.5 Combination of wind, wave and flow |
每根系泊缆由钢丝绳和锁链构成,分为 2 段,钢丝绳连接到导缆孔处,锁链连接到锚处。表 6 给定了所设计的系泊缆参数。
|
|
表 6 钢丝绳和锁链的参数 Tab.6 Parameters of wire and chain |
计算不同组合情况下半潜式平台升沉运动幅值,作为对比半潜式平台时域条件下平台的运动响应情况。表 7 给出了半潜式平台在不同组合工况下平台升沉运动的最大值、平均值以及最小值。
|
|
表 7 平台升沉运动幅值 Tab.7 Heave motion amplitude of semi-submerible platform |
从表中平台升沉运动幅值可以看出,当风、浪、流入射角为 0°,45°,30° 时平台升沉幅值最大,此时为最危险工况。在正常工作条件下,半潜式平台垂荡运动的幅度一般控制在 3 m 左右,半潜式平台升沉运动最大幅值为 2.733 m,符合作业要求。
3.4 系泊线拉力对比分析及安全校核 3.4.1 系泊线与平台连接处的模拟系泊线与平台之间的连接采用的是 2 种模拟方法:扭转弹簧与线性弹簧模拟,认为系泊线与平台连接处模拟弹簧的刚度很大,这样可认为系泊线的作用力直接作用在平台上,此时,作用力为:
| $N_{i}^{S}=K_{i}^{S}({{X}_{i}}+{{p}_{i}}+{{\theta }_{j}}\times {{p}_{k}}-{{r}_{i}}).$ | (3) |
式中:
对于半潜式平台来说,平台运动以及受力过大有可能会引起系泊线的断裂,对半潜式平台的工作性能产生严重的影响,因此,研究半潜式平台系泊受力分析十分重要。对于系泊线拉力安全性评估,可参照 DNV RP 205 规范,对半潜式平台锚泊线进行安全校核,根据校核标准,当系泊缆完整时,要求的安全系数为 1.5。本文选取在相应风、浪、流组合下产生最大拉力的系泊线作为分析对象,计算的结果如表 8 所示。
|
|
表 8 系泊线拉力及安全校核 Tab.8 Mooring line tension and security check |
当风、浪、流为不同组合时,系泊线所承受的拉力大小不同,但所设计的系泊缆安全系数均大于 1.50,说明设计的系泊缆可以满足作业需求。
4 结语1)对半潜式平台时域与频域运动响应进行预报可知,频域分析适合预报非线性影响较小的响应,适合于平台的初步设计及选型阶段。时域分析可以预报非线性较强的响应,预报较为精确,但时域分析耗时较长,计算复杂,适合后期的设计阶段。
2)对比不同工况组合下对系泊线拉力影响可知:浪、流、风为 0°,45°,30° 以及 180°,135°,150° 时半潜式平台升沉幅值最大,最大幅值为 2.733 m,同时系泊线产生的拉力最大,为最危险工况,但安全系数均大于 DNV 规范要求的 1.50,即所设计的系泊线符合安全规范的要求。
| [1] |
王俊荣, 谢彬. 半潜式平台水动力性能及运动响应研究综述[J]. 中国造船 , 2009, 50 (S) :255–261.
WANG Jun-rong, XIE Bin. Review of hydrodynamic properties and global motion prediction of semi-submersible[J]. Shipbuild-ing of China , 2009, 50 (S) :255–261. |
| [2] | YANG Li-jun, XIAO Long-fei, YANG Jian-min. Review on the study of hydrodynamics of semi-submersible platforms[J]. China Offshore Platform , 2009, 24 (1) :1–9. |
| [3] |
孟昭瑛, 任贵永. 半潜式平台工作原理和结构特点分析[J]. 中国海洋平台 , 1995, 10 (1) :35–37.
MENG Zhao-ying, REN Gui-yong. Working principle and structural characteristic analysis of semi-submersible platforms[J]. China Offshore Platform , 1995, 10 (1) :35–37. |
| [4] | 陈鹏.深水半潜式平台系泊系统耦合动力响应研究[D].大连:大连理工大学, 2010. http://cdmd.cnki.com.cn/article/cdmd-10141-1011021344.htm |
| [5] |
张威, 冯玮, 谢彬. 深水半潜式平台运动响应预报方法的对比分析[J]. 中国海上油气 , 2009, 21 (1) :61–64.
ZHANG Wei, FENG Wei, XIE Bin. Comparative analysis on forecasting procedures of deepwater semi-submersible platform motion-response[J]. China Offshore Oil and Gas , 2009, 21 (1) :61–64. |
| [6] |
刘应中, 缪国平, 李谊乐, 等. 系泊系统动力分析的时域方法[J]. 上海交通大学学报 , 1997, 31 (11) :7–12.
LIU Ying-zhong, MIAO Guo-ping, LI Yi-le, et al. A time do-main computation method for dynamic behavior of mooring system[J]. Journal of Shanghai Jiaotong University , 1997, 31 (11) :7–12. |
| [7] | 聂武, 刘玉秋. 海洋工程结构动力分析[M]. 哈尔滨: 哈尔滨工程大学出版社, 2002 . |
| [8] | YILMAZ O, INCECIK A. Extreme motion response analysis of moored semi-submersibles[J]. Ocean Engineering , 1996, 23 (6) :497–517. DOI:10.1016/0029-8018(95)00057-7 |
 2016, Vol. 38
2016, Vol. 38
