随着陆地石油资源的不断减少,人们把目光转移到海洋。近年来,海洋石油的开发和利用越来越频繁,而且逐渐从浅水向深水发展[1]。张力腿平台是一种适用于深水的海洋平台,因此对张力腿平台进行探索和研究成为热点[2]。
张力腿平台与其他平台相比,具有诸多优势[3]。首先,受张力筋腱的影响,当平台处于平衡位置时,垂荡非常小,在风浪等载荷的作用下,移动相对较小,平台安全稳定;其次,张力腿平台在采油时,不需要辅助钻井船,降低了生产成本;而且张力腿平台既适用于几百米的浅水,也适用于上千米的深水甚至是超深水,既适用于小型油田,又适用于大规模的区块油田。但张力腿平台在运营过程中会因为种种原因毁坏,其中疲劳破坏是最常见的原因之一[4]。而结构的疲劳破坏会对海洋石油的开采、工作人员的安全及海洋环境都会产生影响。因此,为保证张力腿平台的安全性,并使其经济效益最大化,对张力腿平台进行疲劳寿命预报,疲劳强度分析与校核就显得尤为重要[5-7]。
目前,对于张力腿平台,研究总体强度和耦合运动响应的比较多[8];而对于张力腿平台的疲劳问题,其研究对象大多是系泊系统[9],对张力腿平台主体结构的疲劳强度研究较少。本文利用 SESAM 软件,对张力腿平台主体结构进行疲劳强度分析,并在分析过程中,研究关键节点有限元模型的划分方法,总结网格划分过程中的经验。
1 疲劳分析的谱分析法谱分析法是海洋平台疲劳强度分析过程中比较常用的分析方法,中心思想是首先求解出海洋平台受到的波浪载荷,然后通过解析方法得到结构的波浪力谱,最后施加到海洋平台上,得到结构应力响应谱[10];也可通过数值分析方法,直接获得海洋平台的应力响应谱,然后结合结构响应谱的统计特性、应力响应的分布特性及 Miner 累积损伤理论来预报海洋平台的疲劳寿命。采用谱分析法计算结构疲劳寿命的具体过程如下:
1)计算应力传递函数和应力响应谱
假设波浪是一个平稳的随机过程,经过变换得到的交变应力也是一个平稳的随机过程,由随机过程理论,上述 2 个平稳随机过程的功率谱密度之间有下列关系:
| ${{S}_{\sigma }}\left( \omega |{{H}_{S}},{{T}_{Z}},\theta \right)={{\left| H\left( \omega |\theta \right) \right|}^{2}}\cdot {{S}_{\eta }}\left( \omega |{{H}_{S}},{{T}_{Z}} \right)。$ | (1) |
式中:$ {S_\sigma }(\omega |{H_S},{T_Z},\theta ) $ 为应力响应谱;$ H\left( {\omega |\theta } \right) $ 为结构应力响应的传递函数;$ {S_\eta }\left( {\omega |{H_S},{T_Z}} \right) $ 为波浪谱;HS 为有义波高;TZ 为波浪平均跨零周期;ω 为波浪频率;θ 为浪向。
2)计算应力响应谱的 n 阶谱矩
| ${{m}_{n}}=\int\limits_{0}^{+\infty }{{{\omega }^{n}}}\cdot {{S}_{\sigma }}\left( \omega |{{H}_{S}},{{T}_{Z}},\theta \right)\text{d}\omega \text{,}$ | (2) |
| ${{T}_{Z}}=2\pi \sqrt{\frac{{{m}_{0}}}{{{m}_{2}}}},$ | (3) |
| $\sigma =\sqrt{{{m}_{0}}}\text{。}$ | (4) |
式中:mn 为应力响应谱的 n 阶矩;σ 为短期瑞利分布的均方差;TZ 为波浪平均跨零周期。
3)求应力响应短期分布概率密度函数
假定各个短期海况应力响应分布若符合 Rayleigh 分布,概率密度函数形式如下:
| $\sigma =\sqrt{{{m}_{0}}}。$ | (5) |
式中:S 为应力范围;$ \sigma= \sqrt {{m_0}} $。
4)计算某一短期海况的疲劳损伤
波浪载荷是随机载荷,其在结构内引起的交变应力也是一随机过程,因此结构在某浪向、某短期海况作用下的疲劳累积损伤度可用下式表示:
| ${{d}_{ij}}=\frac{{{N}_{L}}}{A}\int\limits_{0}^{+\infty }{{{S}^{m}}}g\left( S \right)\text{d}S\text{。}$ | (6) |
式中:NL 为在所考虑的整个设计期内应力范围的总循环次数;A和m 为 S-N 曲线的参数。
5)计算总的疲劳损伤值
考虑各个浪向的概率以及该浪向下的各短期海况,可以计算得到总的疲劳累积损伤为:
| $D=\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{k}{{{p}_{s,i}}}}{{p}_{d,j}}{{d}_{ij}}。$ | (7) |
式中:n 为短期海况的个数;k 为浪向的个数;ps,i 为某一海况 i 的发生概率;pd,j 为某一浪向 j 的分布概率;dij 为在某一海况、某一浪向下的疲劳损伤度。
2 张力腿平台疲劳寿命分析 2.1 有限元模型的建立张力腿平台主要由下浮体、立柱及上部甲板组成,采用 SESAM 软件的 GeniE 模块建立有限元模型,如图 1 所示,平台主尺度信息如表 1 所示。

|
图 1 有限元模型 Fig. 1 Finite element model |
|
|
表 1 主尺度信息 Tab.1 Information of main scale |
在建立整体有限元模型的过程中,采用 2 m 的网格密度,由板单元、梁单元和质量块组成,共有 34 588 个节点和 48 058 个单元。
2.2 疲劳关键节点的选取研究表明,疲劳破坏往往发生在结构的不连续处和应力集中的焊接节点处,对张力腿平台所有可能发生疲劳破坏的区域进行疲劳强度分析的工作量大,可行性差。比较合理的做法是:根据总体强度分析结果来筛选关键区域,在此过程中,要重点关注对总体强度影响较大的不连续处的焊接节点[11]。
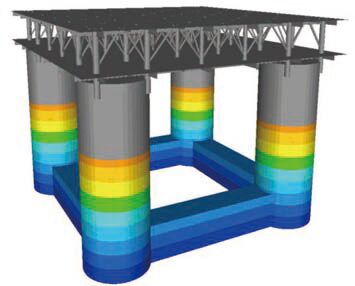
本文通过 SESAM 的 Wadam 模块对张力腿平台进行水动力分析,得到一阶波浪力、附加质量和附加阻尼等水动力基本参数,然后通过 SESAM 的 Sestra 模块对张力腿平台进行总体强度分析,总体强度分析结果如图 2 所示,图 3 和图 4 分别为张力腿平台所受的静水压力示意图和波浪载荷示意图。

|
图 2 总体强度分析 Fig. 2 Analysis of overall strength |
|
图 3 静水压力示意图 Fig. 3 Diagram of hydrostatic pressure |

|
图 4 波浪载荷示意图 Fig. 4 Diagram of wave load |
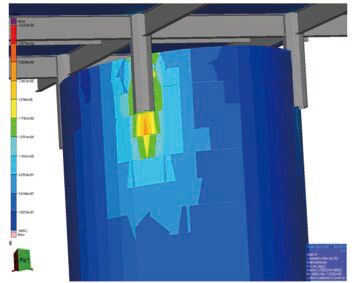
从图 2 可看出,此张力腿平台整体应力分布均匀合理,在立柱与下浮体连接处和立柱与上甲板连接处的应力比较大,图 5 和图 6 分别为这两处的局部放大图,而且这两处恰恰是结构不连续处的焊接节点。因此疲劳关键区域选为立柱与下浮体连接处和立柱与上甲板连接处。确定疲劳关键区域后,疲劳关键节点的坐标也随之确定,如表 2 所示。

|
图 5 立柱与下浮体连接处 Fig. 5 Connection of column and pontoon |
|
图 6 立柱与甲板连接处 Fig. 6 Connection of column and deck |
|
|
表 2 疲劳关键节点坐标 Tab.2 Coordinate of fatigue critical node |
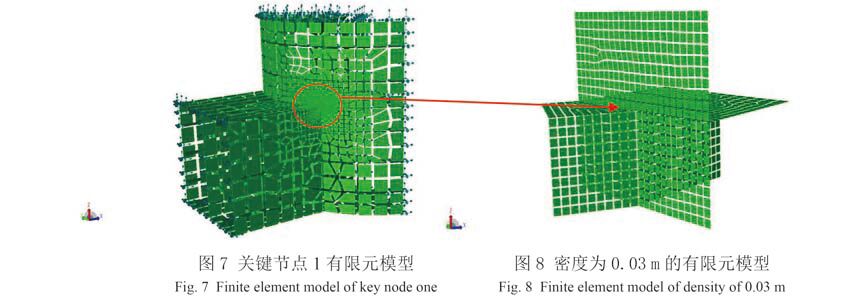
如图 2 所示,把立柱与下浮体连接处定为关键节点 1,立柱与上甲板连接处定为关键节点 2,通过 GeniE 模块建立关键节点的有限元模型,网格划分后的模型如图 7 和图 9 所示。
|
图 7 关键节点 1 有限元模型 Fig. 7 Finite element model of key node one |
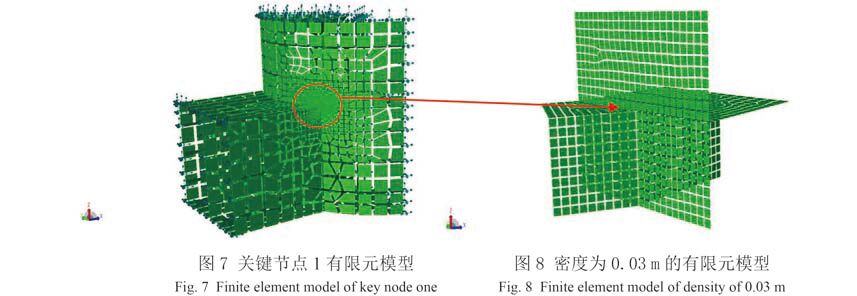
|
图 8 密度为 0.03 m 的有限元模型 Fig. 8 Finite element model of density of 0.03 m |
|
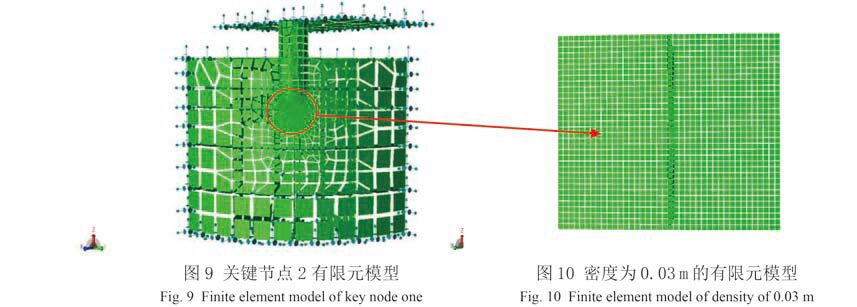
图 9 关键节点 2 有限元模型 Fig. 9 Finite element model of key node one |
根据局部模型边界节点的坐标,在整体模型中取出相应位置节点的位移,作为局部模型的边界条件,利用 SESAM 的 Submod 模块,将总体强度模型中节点的状态传递给子模型。因此,在局部有限元模型网格划分时,特别注意边界处网格单元的大小和位置应与整体模型完全一致。
利用 SESAM 软件对网格进行划分的过程中,如果处理的不恰当,在不同网格密度的过渡区域会出现畸形网格,这样将无法进行疲劳动载荷的计算,也就无法对热点进行疲劳分析,因此要花费很多时间来调整网格密度的大小和不同网格密度板的大小。有时对于个别出现畸形网格的地方,通过插入 Feature edge 来调整局部网格。
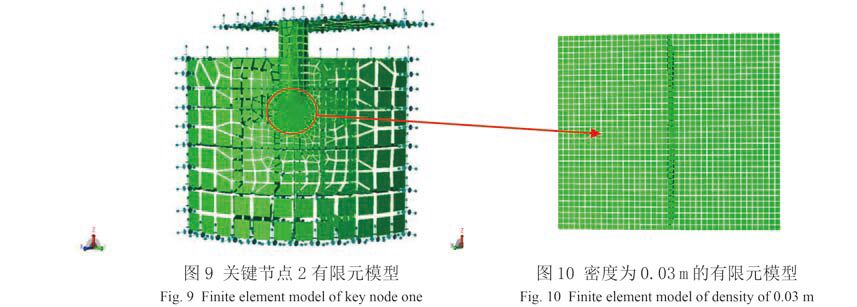
在网格划分过程中,网格要实现平稳过渡,且要求疲劳热点部位的网格大小为 t×t,其中 t 为疲劳关键节点处的板厚。在实际划分网格的过程中,用的网格密度为 0.03 m,0.1 m,0.5 m,1 m 和 2 m,从里向外逐渐增大,热点区域的网格密度约为板厚 0.03 m,这样算出来的热点应力更为准确,图 8 为立柱与下浮体连接处密度为 0.03 m 的有限元模型,图 10 为立柱与甲板连接处密度为 0.03 的有限元模型。边界区域的网格密度为 2 m,这是因为总体模型中的网格密度为 2 m,在获取子模型的边界条件时,边界上的节点可以吻合。
|
图 10 密度为 0.03 m 的有限元模型 Fig. 10 Finite element model of density of 0.03 m |
在 Wadam 中进行水动力分析时,环境参数为:浪向角为 180°~270°,间隔 10°,等概率分布;周期为 2~32 s,间隔 2 s;海浪谱采用 Pierson Moskowitz(P-M) 谱,根据中国南海海浪长期资料,可得到此海域波浪参数的统计值如表 3 所示。
|
|
表 3 南海海况统计资料 Tab.3 Statistics of the South China Sea |
通过 Wadam 进行水动力分析,然后 Sestra 计算关键节点的应力传递函数,最后导入 Stofat 进行疲劳寿命预报。
Stofat 在计算热点应力时,根据 ABS 规范[12]采用外推法。S-N 曲线的选取,同样根据 ABS 规范。对于非管节点结构,在计算结构的疲劳寿命时,采用 E 曲线;关键节点 1(立柱与下浮体连接处)在海水中,所以采用 ABS-E-CP 曲线;关键节点 2(立柱与上甲板连接处)暴露在空气中,所以采用 ABS-E-A 曲线。它们的参数如表 4 所示。
|
|
表 4 S-N 曲线参数 Tab.4 Parameter of S-N curve |
本文张力腿平台的疲劳设计寿命为 20 年,根据 ABS 规范[12],疲劳安全因子应分别取为 3,最后通过 Stofat 计算出关键节点处的疲劳寿命如表 5 所示。
|
|
表 5 关键节点疲劳寿命结果 Tab.5 Fatigue life of critical node |
海洋平台结构疲劳强度评估是平台结构安全评估的重要内容之一。本文应用 SESAM 软件,对一张力腿平台关键部位进行了疲劳强度研究,其主要结论如下:
1)通过对张力腿平台的总体强度分析,获得了平台容易产生疲劳破坏的 2 个关键节点,分别为立柱与下浮体连接处和立柱与甲板连接处。
2)利用 SESAM 软件对结构的疲劳强度进行分析的过程中,特别要注意关键节点有限元模型的网格划分,建议采用多梯度平稳过渡的方法,这样可以避免畸形网格的产生,从而使疲劳关键节点的应力更加准确。应该在局部模型的边界处设置与整体模型中相同的网格密度,并且局部模型的边界应在舱壁、T型材和加强筋处,这样与整体模型中的网格能够吻合,从而使局部模型获得更加精确的边界条件。
3)对关键节点进行疲劳寿命分析结果表明,立柱与下浮体连接处的疲劳寿命为 62.7 年;立柱与甲板连接处的疲劳寿命为 148 年。本平台的设计寿命是 20 年,安全因子为 3,疲劳寿命预报结果表明关键节点满足设计要求。相比较而言,立柱与下浮体连接处的疲劳损伤度大,疲劳寿命短,而且该位置处于海水中,如果发生疲劳破坏不易被发现,因此应进行定期的检查和维护。
| [1] |
李润培, 谢永和, 舒志. 深海平台技术的研究现状与发展趋势[J]. 中国海洋平台 , 2003, 18 (3) :1–5.
LI Run-pei, XIE Yong-he, SHU Zhi. A review on the technical development of deep water offshore platform[J]. China Off-shore Platform , 2003, 18 (3) :1–5. |
| [2] |
杨雄文, 樊洪海. TLP平台结构型式及其总体性能分析[J]. 石油机械 , 2008, 36 (5) :70–73.
YANG Xiong-wen, FAN Hong-hai. Analysis of TLP structure and its overall performance[J]. China Petroleum Machinery , 2008, 36 (5) :70–73. |
| [3] |
张智, 董艳秋, 唐友刚, 等. 1990年后世界TLP平台的发展状况[J]. 中国海洋平台 , 2004, 19 (2) :5–11.
ZHANG Zhi, DONG Yan-qiu, TANG You-gang, et al. The development of TLP after 1990[J]. China Offshore Platform , 2004, 19 (2) :5–11. |
| [4] | 陈新权.深海半潜式平台初步设计中的若干关键问题研究[D]. 上海:上海交通大学, 2007. http://mall.cnki.net/magazine/article/zghy201102011.htm |
| [5] |
崔磊, 何勇, 徐伽南, 等. 张力腿平台关键部位疲劳可靠性分析[J]. 海洋工程 , 2013, 31 (1) :16–25.
CUI Lei, HE Yong, XU Jia-nan, et al. Fatigue reliability analyses on key parts of tension leg platform[J]. The Ocean Engineering , 2013, 31 (1) :16–25. |
| [6] |
陈团海, 陈国明. 冰区平台疲劳可靠性与参数敏感性分析[J]. 船海工程 , 2009, 38 (5) :129–133.
CHEN Tuan-hai, CHEN Guo-ming. Analysis on reliability and parameters sensitivity of fatigue of offshore platform in ice region[J]. Ship & Ocean Engineering , 2009, 38 (5) :129–133. |
| [7] |
杨鹏, 顾学康. 半潜平台结构疲劳寿命评估方法比较[J]. 舰船科学技术 , 2012, 34 (8) :112–118.
YANG Peng, GU Xue-kang. Comparative researches of structural fatigue life assessment procedures for a semi-submersible platform[J]. Ship Science and Technology , 2012, 34 (8) :112–118. |
| [8] |
谷家扬, 吕海宁, 杨建民. 张力腿平台在随机波浪中的耦合运动响应研究[J]. 船舶力学 , 2013, 17 (8) :888–900.
GU Jia-yang, LV Hai-ning, YANG Jian-min. Studies on coupling dynamic response of TLP in stochastic waves[J]. Journal of Ship Mechanics , 2013, 17 (8) :888–900. |
| [9] |
余建星, 张中华. 波、流联合作用下张力腿平台系索系统疲劳可靠性分析方法研究[J]. 海洋技术 , 2009, 28 (2) :69–72.
YU Jian-xing, ZHANG Zhong-hua. Research on fatigue reliability of tension leg platform tendon system under wave and cur-rent[J]. Ocean Technology , 2009, 28 (2) :69–72. |
| [10] |
梁瑜. 基于谱分析法的半潜平台疲劳强度研究[J]. 船海工程 , 2012, 41 (1) :77–80.
LIANG Yu. Fatigue strength assessment for semi-submerged platform based on the spectral-based analysis[J]. Ship & ocean Engineering , 2012, 41 (1) :77–80. |
| [11] | 白艳彬.深水半潜式钻井平台总体强度分析及疲劳强度评估[D]. 上海:上海交通大学, 2010. http://cdmd.cnki.com.cn/article/cdmd-10248-2010204024.htm |
| [12] | ABS. Guide for the fatigue assessment of offshore structures[S]. Houston, TX:American Bureau of Shipping, 2003. |
 2016, Vol. 38
2016, Vol. 38
