船舶的快速性是衡量船舶速度性能的关键性指标,也是船舶最重要的性能之一[1-2]。为提高船舶的快速性,除了提高推进效率以外,最重要的就是降低船舶所受流体的阻力。过去的船舶阻力研究主要依赖于船模试验的方法,但船模的试验与实船的运动环境相比差别仍然很大,而且流体的运动规律复杂,船模试验并不能很好地进行船舶阻力优化。而船舶阻力优化方法是研究船舶阻力问题的关键。借助于 Fluent 的仿真模拟,能够较为精确的模拟出船体在不同环境下的运动情况,模拟出船体界面周围的流体、阻力、压强等运动细节[3-6]。本研究通过船体的型线图,采用 GAMBIT 建模及网格划分,模拟其在不同航速下的阻力情况,得到一定速度范围内船速与摩擦阻力和压差阻力的关系。同时通过若干个方形系数不同的船体模型,得到傅汝德数不变时,一定范围内的方形系数和船体阻力的关系,为 Fluent 模拟船舶减阻提供一定的参考依据。
1 计算模型 1.1 模型的建立和网格划分选取的对象是 1 艘 DWT8900 油船,设计水线长 LW1 = 110 m,型宽 B = 18 m,型排水体积 11 388.67 m3,设计吃水 T = 6.5 m,方形系数为 0.884 9。在 FLUENT 中调整缩尺比为 1∶1 000。实船与模型的主要数据如表 1 所示。
|
|
表 1 油船主尺度 Tab.1 Main dimensions of ship |
采用长方体作为控制域,由于半个船模的长宽高分别为 110 mm,9.05 mm,9 mm,因此本例选择沿船首方向延长 1 倍船长,沿船尾方向延长 4 倍船长,沿船两侧延长 1 倍船长,沿船舶垂线上下各延长一半船长,建立了一个长 660 mm、宽 110 mm、高 110 mm 的长方体控制域。坐标原点仍然是原船体坐标系的原点。船首与流体入口距离 110 mm,船尾与流体出口距离 440 mm。由于船体的设计水线为 6.5 m,因此该部分区域在垂直方向上流体的自由液面距离控制体顶部的边界为 57.5 mm。以自由液面所在的位置创建 1 条线分割入口面,上部分为空气速度入口,下部分为水速度入口,如图 1 所示。
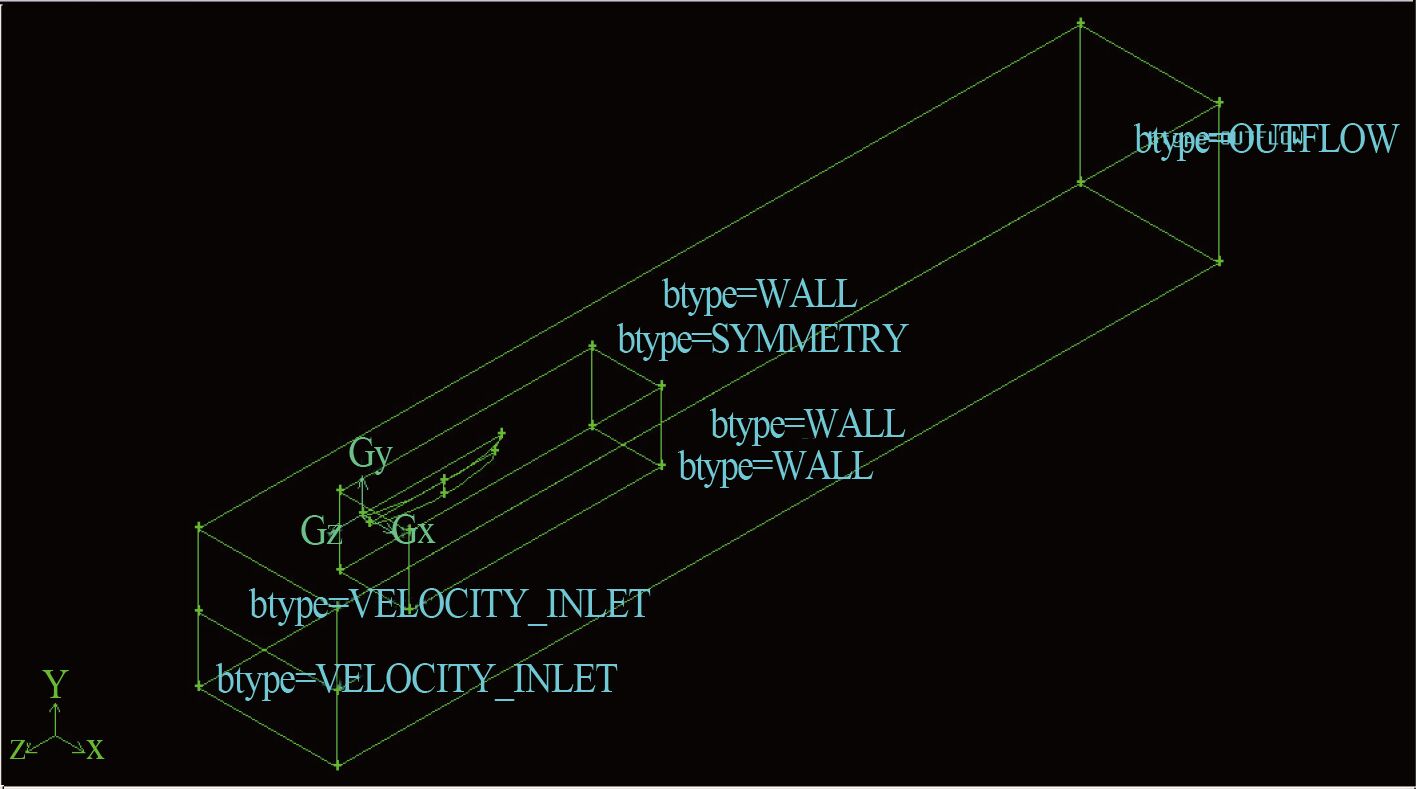
|
图 1 计算域 Fig. 1 Computational domain |
船体周围网格对船体表面分析影响较大,采用从线网格到面网格再到体网格的顺序[10-11]。其中面网格划分情况如图 2 所示。
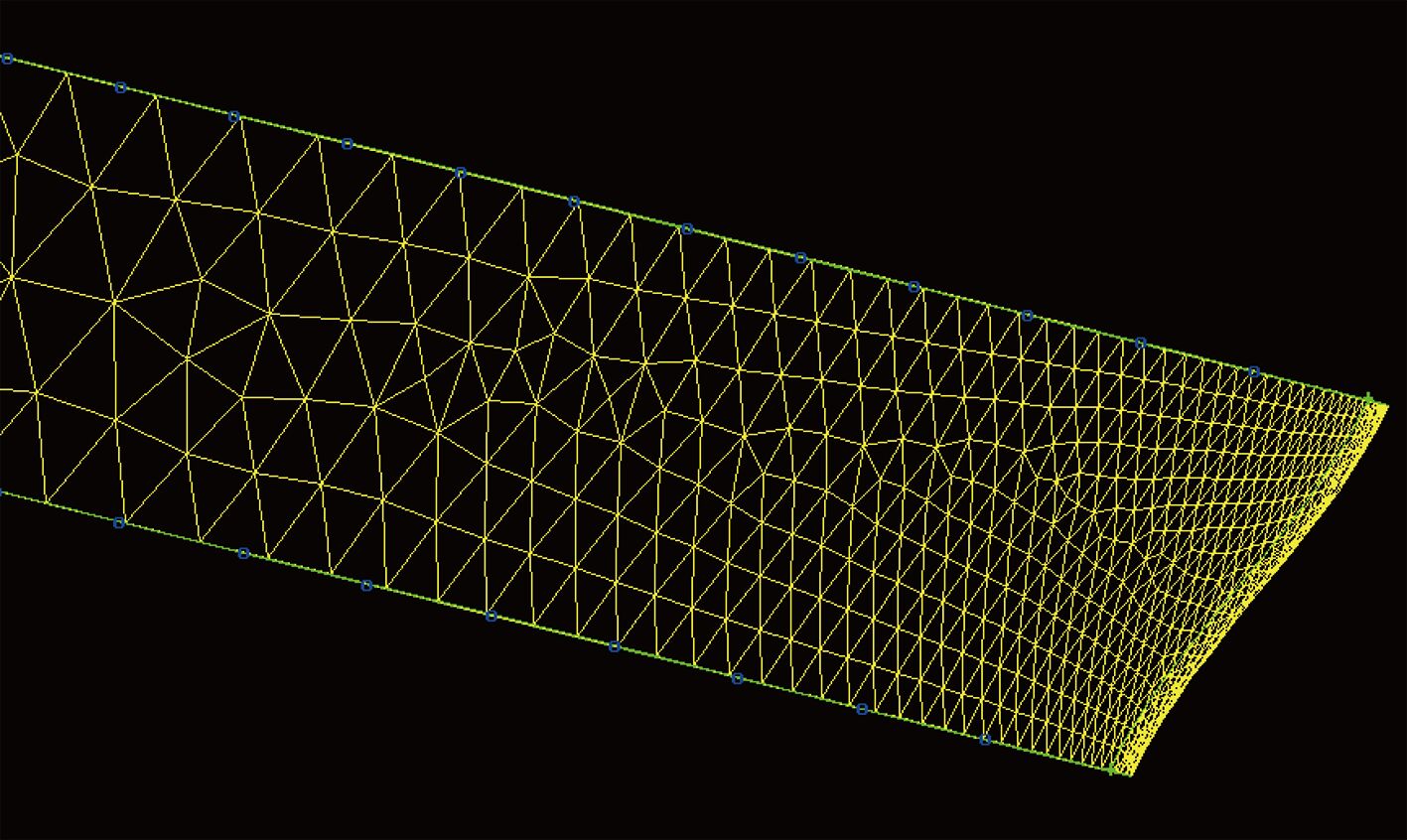
|
图 2 船体局部面网格 Fig. 2 Local surface meshes on the hull |
在定义求解器时候选择 unsteady 非稳态求解,选定多相流模型 Volume of Fluid,湍流模型选取 k-epsilon-RNG。设定出口边界条件为 outflow 自由出口,首先定义的是空气速度入口,在混合相 Mixture 中定义空气入口 air-inlet 为速度入口 velocity-inlet,设在 Phase 相中选择 water,在 multiphase 中选定 Volume Fraction 为 0,并确保空气域中水的比例为 0。之后定义水的速度入口,在混合相 Mixture 中定义水入口 water-inlet 为速度入口 velocity-inlet。在 Phase 相中选择 water,在 multiphase 中选定 Volume Fraction 为 1,并确保水域中水的比例为 1,不存在空气。定义对称面为 symmetry,其余边界默认为 wall。设定时间步长为 0.001,总步数为 1 000,每个时间步内最大的迭代次数为 10,在刚开始的时候选择较小的时间步长迭代一定次数,当残差不是太大的时候再扩大时间步,这样既保证计算收敛,又可缩短计算时间,提高计算效率[7]。通过计算后处理得到的船体气液两相分布如图 3 所示。
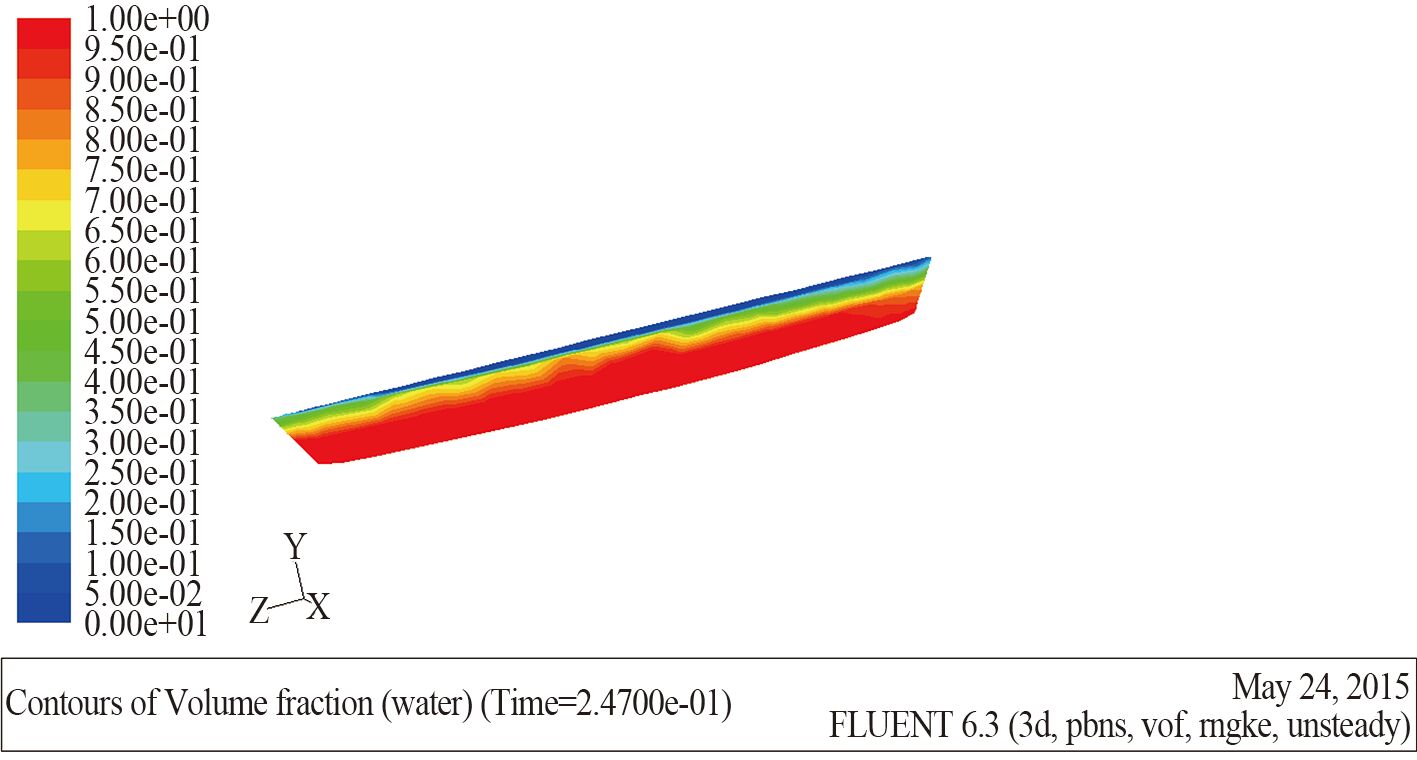
|
图 3 船体气液两相分布图 Fig. 3 Hull gas-liquid two-phase distribution |
依然选择 DWT8900 油船作为计算对象,计算选取船模航速为 1.0 m/s,2.0 m/s,2.5 m/s,5 m/s,继续采用相同的网格计算船模总阻力,在 Fluent-Report-Force 中得到摩擦阻力和压差阻力,如表 2 所示。
由表 2 格可见,随着船速的增加,基本阻力非线性增大,且当船速较低时,基本阻力增大较为缓慢,船速较高时,基本阻力显著增大。通过摩擦阻力的占比可知,船速较低时,摩擦阻力占基本阻力的绝大部分,随着船速的提高,则压差阻力占的百分数将越来越大。表明船速较高时兴波阻力显著增大,使得压差阻力的占总阻力的占比显著增大。因此,在船舶减阻过程中,在低速时主要应该降低摩擦阻力;在高速时主要应该降低兴波阻力。
|
|
表 2 船体不同航速下阻力情况分析 Tab.2 Analysis of different resistance at lower hull speed |
以 1 艘船长 L = 124 m、型宽 B = 17.6 m,型深 D = 10.9 m,型吃水 d = 5.5 m 的 1 艘 7 500 t 的海洋客货船为例,仅考虑其方形系数对于阻力的影响,根据方形系数公式${C_b} = \displaystyle \frac{\Delta }{{L \times B \times d}}$,在控制 L,B,d 不变的情况下在 Gambit 建立 3 个船体肥瘦程度不同的船体,即通过 Gambit 建模改变船体水下表面肥瘦程度来改变船体的排水体积,从而得到 3 个方形系数不同的船体模型,具体数值如表 3 所示。
|
|
表 3 三种船型的主尺度 Tab.3 Main scales of three different ship styles |
为更加直接的体现方形系数和船体阻力的关系,引入单位排水量总阻力的概念,即探讨方形系数 Cb 与单位排水量摩擦阻力 $\displaystyle \frac{{{R_f}}}{\Delta }$、单位排水量压差阻力 $\displaystyle \frac{{{R_\varepsilon }}}{\Delta }$ 的关系,如表 4 所示。
|
|
表 4 方形系数与单位排水量阻力关系 Tab.4 The relationship of block coefficient and unit displacement resistance |
从表 4 中可看出,当流体速度在 2.5 m/s、方形系数在 5.517 2~0.607 6 范围内时,随着方形系数的增大,船体单位排水量的摩擦阻力和单位排水量的压差阻力均呈非线性增大;当方形系数由 0.517 27 增长到 0.561 23 时,船体的单位排水量摩擦阻力增大 8.57%、单位排水量压差阻力增大 15.7%;当方形系数由 0.561 23 增长到 0.607 60 时,船体的单位排水量摩擦阻力增大 4.38%,单位排水量压差阻力增大 10.39%。这说明了船舶方形系数对船体摩擦阻力影响较小,但对船体的压差阻力影响较大。
以上得到了在 v = 2.5 m/s 一定的情况下,即傅汝德数 Fn 一定的情况下,一定范围内的方形系数和船体的阻力的关系,由于计算时间的原因本文只选择了 3 个船模代表的方形系数进行分析,若通过更多的船模在 Fluent 里的仿真模拟,可以得到一个阻力最低的最佳方形系数和一个阻力显著增加的临界方形系数。选择合适的方形系数降低船舶阻力还需考虑方形系数对船体布置的影响,大的方形系数有利于船体内部的舱室布置;小的方形系数则因过于尖瘦往往会给布置带来困难。
因此,选择合适的方形系数减小阻力,还需要考虑到船舶主尺度的变化带来的经济性[8]。超过临界方形系数时阻力急剧增大会使得主机功率、燃油消耗、燃料开支均增大。选用最佳方形系数时可使得船体压差阻力显著下降。但是由于选择最佳方形系数船体过于瘦削,为了保证一定的排水量,船体的主尺度就要增大,船体主尺度的增大又会增加船体的摩擦阻力。因此,应根据 Fluent 多次模拟得到的船体最佳方形系数与船体的经济性综合考虑才能得到最合适的方形系数。
3 结语借助 Fluent 分别模拟了不同航速下船模的运动情况,得出了船体在一定条件下的受力情况。通过不同条件下的 Fluent 仿真模拟得到了以下结论:
1)在一定速度范围内,随着船速的增加,基本阻力非线性增大,且当船速较低时,基本阻力增大较为缓慢,船速较高时,基本阻力显著增大。船速较低时,摩擦阻力占基本阻力的绝大部分,随着船速的提高,则压差阻力占的百分数将越来越大。
2)速度不变即傅汝德数 Fn不变的情况下,在一定方形系数范围内,随着方形系数的增大,船体单位排水量的摩擦阻力和单位排水量的压差阻力均呈非线性增大。且船舶方形系数对船体摩擦阻力影响较小,但对船体的压差阻力影响较大。
| [1] |
邵世明, 赵连恩, 朱念昌.
船舶阻力[M]. 北京: 国防工业出版社, 1995 .
SHAO Shi-ming, ZHAO Lian-en, ZHU Nian-chang. Ship resistance[M]. Beijing: National Defense Industry Press, 1995 . |
| [2] |
蒋维清.
船舶原理[M]. 大连: 大连海事大学出版社, 1998 : 133 -134.
JIANG Wei-qing. Ship principle[M]. Dalian: Dalian Maritime University Press, 1998 : 133 -134. |
| [3] |
黄德波.近年我国船舶阻力方面的若干研究[C]//中国造船工程学会船舶力学学术委员会成立三十周年暨第七届学委会全体会议论文集. 成都:中国造船工程学会, 2010.
HUANG De-bo. Several studies in recent years, China's ship-building resistance aspect[C]. Chengdu:China's Society of Naval Architecture and Marine Engineers, 2010. |
| [4] |
倪崇本.基于CFD的船舶阻力性能综合研究[D].上海:上海交通大学, 2011.
NI Chong-ben. A comprehensive investigation of ship resistance prediction based on CFD theory[D]. Shanghai:Shanghai Jiao Tong University, 2011. |
| [5] |
余建伟.基于CFD的船舶阻力计算与预报研究[D].上海:上海交通大学, 2009.
YU Jian-wei. Research on calculation and prediction for ship resistance based on CFD theory[D]. Shanghai:Shanghai Jiao Tong University, 2009. http://cdmd.cnki.com.cn/article/cdmd-10248-2009225651.htm |
| [6] |
郑小龙, 黄胜, 尚秀敏. 基于CFD的船舶阻力预报方法研究[J]. 江苏科技大学学报(自然科学版) , 2014, 28 (2) :109–113.
ZHENG Xiao-long, HUANG Sheng, SHANG Xiu-min. Study of ship resistance prediction method based on CFD[J]. Jiangsu University of Science and Technology (Natural Science Edition) , 2014, 28 (2) :109–113. |
| [7] |
常欣, 郭春雨, 王超, 等.
Fluent船舶流体力学仿真计算工程应用基础[M]. 哈尔滨: 哈尔滨工程大学出版社, 2011 .
CHANG Xin, GUO Chun-yu, WANG Chao, et al. Fluent ship hydrodynamics simulation-based engineering applications[M]. Harbin: Harbin Engineering University Press, 2011 . |
| [8] |
段晔鑫, 刘源, 王毅, 等. 五体船侧体布局及兴波阻力优化[J]. 舰船科学技术 , 2015, 37 (3) :10–14.
DUAN Ye-xin, LIU Yuan, WANG Yi, et al. Research on the demihulls layout and wave resistance optimization of pentamaran[J]. Ship Science and Technology , 2015, 37 (3) :10–14. |
 2016, Vol. 38
2016, Vol. 38
