2. 海军装备研究院, 北京 100161
2. Naval Academy of Armament, Beijing 100161, China
带前置定子导管桨是一种新型组合式推进器,具有高效低噪声的优点,在水下航行体上应用较广泛。由于该组合式推进器螺旋桨与导管之间存在间隙,在螺旋桨旋转形成的压力面和吸力面之间的压差作用下,梢隙处往往会形成梢涡,当环境压力较低时会产生梢涡空泡,极易导致螺旋桨空泡剥蚀,加剧幅射噪声,是推进器设计者的难题。
常见的螺旋桨空泡类型有梢涡空泡、泡空泡及叶面片空泡等。在空泡理论和空泡试验方面开展过大量的研究,McCormich,Billet & Holl Chow 和 Fruman et al.[1-4]等都对梢涡形成进行定义及用各种涡模型来评估模拟涡核半径、涡内最小压力值及涡周围流场。
近年来,CFD 方法的迅速发展并且在许多领域迈向实用化,使得用 CFD 方法研究螺旋桨空泡成为可能。Senocak & Shhy[5-6]数值模拟了二维翼型和圆头形的轴对称体的空泡流动,得到的壁面压力系数与试验值吻合较好。Shin Hyung Rhee 和 Kawamura[7]利用 Fluent 数值预报了 4 叶螺旋桨空泡形态,预报结果与试验结果吻合较好。刘登成[8-9]也对螺旋桨空泡形态和三维扭曲水翼非定常空泡进行了数值模拟。
本文采用基于混合网格的 RANS 求解器结合 Singal 空泡模型,数值模拟带前置定子导管桨片空泡形态,对水下航行体后带前置定子的导管桨多个方案全湿流动进行数值模拟,通过梢部端面的最小压力值判断空泡起始。
1 数值计算方法 1.1 控制方程控制方程为定常不可压缩 RANS 方程。在直角坐标系下,将控制方程利用基于单元中心的有限体积法进行离散,对流项使用二阶迎风格式,扩散项使用二阶中心差分格式。整体求解过程使用基于适合非结构网格的 SIMPLE 算法。离散方程通过 Gauss-Seidel 方法迭代求解,用代数多重网格技术来加速解的收敛。
流场数值求解基于守恒张量形式的连续性方程和动量方程,其表达如下:
| $\frac{\partial \left( {{\rho }_{m}}{{u}_{i}} \right)}{\partial {{x}_{i}}}=0\text{,}$ | (1) |
| $\frac{\partial \left( {{\rho }_{m}}{{u}_{i}}{{u}_{j}} \right)}{\partial {{x}_{j}}}=-\frac{\partial p}{\partial {{x}_{i}}}+\frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu +{{\mu }_{t}} \right)\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right) \right]。$ | (2) |
式中:${\rho _m}$ 为密度;${\mu _t}$ 为混合涡粘性系数;${u_i}$ 为随体直角坐标中绝对速度矢量的 i 分量;p 为压力。全湿流计算时,${\rho _m}$ 取水的密度;空泡流计算时,${\rho _m}$ 为混合密度,水和汽的密度分别为 998.2 kg/m3 和 0.019 27 kg/m3,而水和汽的运动粘性系数分别为 1.003 × 10-6 和 8.8 × 10-6。
控制方程中湍流运动引起的涡粘性系数,需要使用湍流模型来计算这一项,以实现控制方程的湍流封闭。本文采用标准的 k-ε 湍流模型。
1.2 空泡模型空泡计算时,流体的混合密度 ${\rho _m}$ 是由输运方程所控制的流体质量分数 f 的函数:
| $\frac{1}{{{\rho }_{m}}}=\frac{f}{{{\rho }_{v}}}+\frac{1-f}{{{\rho }_{l}}},$ | (3) |
控制汽体质量分数 f 的输运方程为:
| $\frac{\partial \left( {{\rho }_{m}}f \right)}{\partial t}+\nabla \left( {{\rho }_{m}}\overset{\rightharpoonup }{\mathop{V}}\,f \right)=\nabla \left( \Gamma f \right)+{{R}_{e}}-{{R}_{c}}。$ $ | (4) |
式中:源项 ${R_e}$ 和 ${R_c}$ 分别为汽体生成率和冷凝率,它们均是流场参量(压力、速度)和流体特性(密度、饱和蒸汽压及表面张力)的函数。Singhal.A.K[13]给出源项 ${R_e}$ 和 ${R_c}$ 的表达式如下:
| ${{R}_{e}}=-{{C}_{e}}\frac{\sqrt{k}}{S}{{\rho }_{l}}{{\rho }_{v}}{{\left( \frac{2}{3}\frac{{{p}_{v}}-p}{{{\rho }_{l}}} \right)}^{1/2}}(1-{{f}_{v}}-{{f}_{g}})\text{,if}p<{{p}_{v}}\text{;}$ | (5) |
| ${{R}_{c}}={{C}_{c}}\frac{\sqrt{k}}{S}{{\rho }_{l}}{{\rho }_{l}}{{\left( \frac{2}{3}\frac{p-{{p}_{v}}}{{{\rho }_{l}}} \right)}^{1/2}}{{f}_{v}}\text{,if}p>{{p}_{v}}\text{。}$ | (6) |
式中:${C_e}$ 和 ${C_c}$ 为经验常数,默认值分别为 0.02 和 0.01;k 为湍动能;S 为表面张力;${f_g}$ 为不可冷凝气体质量分数;${f_v}$ 为汽体质量分数。计入湍流脉动影响后的临界饱和蒸汽压为:
| ${{p}_{v}}={{p}_{sat}}+\frac{1}{2}{{p}_{turd}}\text{。}$ | (7) |
式中:${p_{turb}} = 0.39\rho k$;${p_{sat}}$ 为饱和蒸汽压。
1.3 网格生成水下航行体为一回转体。据经验,流体域的选取如下:上游来流入口边界在距水下航行体首部一倍航行体长度处,下游出口边界在距水下航行体尾部 2.5 倍航行体长度处,径向外部边界在离水下航行体轴中心一倍航行体长度处。本文采用多块网格技术,将流体计算区域分为定子区域、螺旋桨区域和外围区域三大块。
网格用商用软件 GAMBIT 生成,如图 1 所示。在物面附近第 1 层网格的 y+ 在 30 ~ 200 之间。其他部分网格的尺寸总体上按 1.2 的比例由物面向外增加,无论是径向还是轴向,网格点的分布均按照“近壁面的区域网格密”的原则。螺旋桨和定子区域采用四面体的非结构化网格。为控制螺旋桨和定子附近区域的网格尺寸,采用 GAMBIT 中的“尺度函数”,网格增长尺寸为 0.5% D(D 为螺旋桨直径),网格增长比率为 1.15,网格最大的限制尺寸为 5% D。螺旋桨推力主要成分由螺旋桨叶背、叶面的压力差引起,所以采用非结构化网格可以较准确地预报。

|
图 1 计算网格示意图 Fig. 1 Sketch map of computational mesh |
利用已建立的螺旋桨空泡粘流数值模拟方法,推广应用于水下航行体后带定子导管桨的片空泡流数值模拟中,对某方案导管桨的片空泡进行数值模拟。图 2 给出了 3 个不同水速空泡数下数值预报的片空泡形态与模型试验结果的对比(试验在中国船舶科学研究中心大型循环水槽进行)。由试验照片可知,3 个工况下在螺旋桨梢部及尾流中均存在明显的梢(隙)涡空泡,而数值预报结果仅在螺旋桨梢部有梢隙涡空泡,在尾流中由于网生分辨率不够没有捕捉到梢涡空泡。当空泡数较小时,螺旋桨叶背的片空泡与梢涡空泡连成了一片;而当适当增大空泡数时,叶背片空泡与梢涡空泡开始分离,处于相互“独立”状态;当进一步增大空泡数时,叶背片空泡消失,只有梢涡空泡存在。

|
图 2 螺旋桨片空泡模拟结果与模型试验结果对比 Fig. 2 The comparison of propeller sheet cavitation between predicted results and model test results |
上述现象与模型试验观测结果完全一致。可见,预报结果较准确地反应出了空泡形状以及空泡发生的大致位置,说明初步建立的水下航行体后带定子的导管桨空泡粘流数值预报方法可行。当然,预报结果与试验结果在细节上还有一些出入,如梢涡空泡的泄出,叶背片空泡发生的精确位置及其脱落等,这些还有待进一步深入研究。
3 梢涡空泡起始判别当流体中某一点压力低于该温度下的饱和蒸汽压时,流体中的气核便会膨胀,最后形成空泡。因此,本文通过梢部端面的最小压力值判断空泡起始。对水下航行体后 3 个导管桨方案多工况下的全湿流动进行了数值模拟,提取了螺旋桨叶梢剖面最小负压值,以此作为梢涡空泡的起始空泡数。
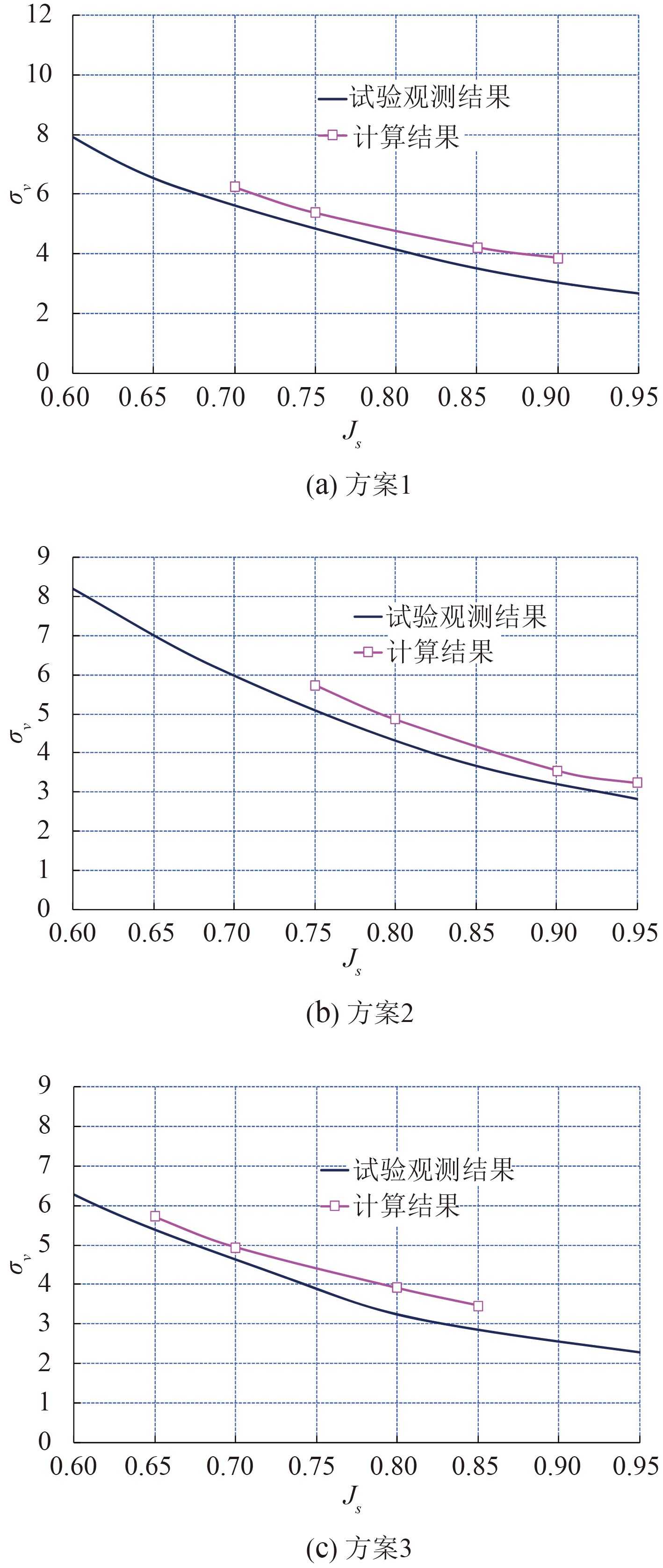
图 3 给出了 3 个导管桨方案螺旋桨梢涡空泡起始预报结果与模型试验结果的对比,螺旋桨叶梢最小负压出现的位置通常在图 4 中所示的 ①~③ 处。由图 3 和图 4 可知,螺旋桨梢涡空泡起始预报结果与试验结果变化趋势吻合较好,且 3 个方案之间的相互大小关系得到了试验验证,这表明利用全湿流计算得到了螺旋桨梢部最小负压值来判别螺旋桨梢涡空泡起始的方法可行,可用于多方案优选,为组合式推进器设计及其梢涡空泡起始优选评估提供了技术手段。
|
图 3 螺旋桨梢涡空泡起始预报结果与模型试验结果对比 Fig. 3 The comparison of propeller tip vortex cavitation inception between predicted results and model test results |
|
|
表 1 三个方案起始空泡数预报结果与试验结果的比较 Tab.1 The comparison of cavitation inception between predicted and model test results |

|
图 4 螺旋桨叶梢最小负压出现位置 |
本文对水下航行体后带前置定子的导管桨片空泡和梢涡空泡起始进行了研究。首先,采用基于混合网格的 RANS 求解器结合 Singal 空泡模型,数值模拟了带前置定子导管桨片空泡形态,并与试验结果进行了对比,预报的片空泡形态与试验结果吻合良好,这表明用该方法预报水下航行体后带前置定子导管桨片空泡可行。其次,对水下航行体后带前置定子的导管桨多个方案全湿流动进行了数值模拟,通过梢部端面的最小压力值判断空泡起始,并与试验结果进行比对,其吻合良好,结果表明可用该方法判别梢隙涡空泡起始。
| [1] | MCCORMICK B W. On cavitation produced by a vortex trailing from a lifting surface[J]. Journal of Basic Engineering , 1962, 84 (3) :369–378. DOI:10.1115/1.3657328 |
| [2] | BILLET M L, HOLL J W. Scale effects on various types of limited cavitation[C]//Proceedings of the International Symposium on Cavitation Inception, the ASME Winter Annual Meeting. New York, NY, USA:ASME, 1979. |
| [3] | CHOW J, ZILLIAC G, BRADSHAW P. Turbulence measurements in the near field of a wingtip vortex[C]//Proceedings of the ASME forum on turbulence in complex flows, Chicago, Illinois, USA. Washington, DC:National Aeronautics and Space Administration, 1997. |
| [4] | FRUMAN D H, CERRUTTI P, PICHON T, et al. Effect of hydrofoil planform on tip vortex roll-up and cavitation[J]. Journal of Fluids Engineering , 1995, 117 (1) :162–169. DOI:10.1115/1.2816806 |
| [5] | SENOCAK I, SHYY W. Numerical simulation of turbulent flows with sheet cavitation[C]//Proceedings of the 4th international symposium on cavitation. Pasadena, CA, USA:California Institute of Technology, 2001. |
| [6] | SENOCAK I, WEI SHYY W. A pressure-based method for turbulent cavitating flow computations[J]. Journal of Computational Physics , 2002, 176 (2) :363–383. DOI:10.1006/jcph.2002.6992 |
| [7] | RHEE S H, KAWAMURA T, LI H Y. A study of propeller cavitation using a RANS CFD method[C]//Proceedings of the 8th International Conference on Numerical ship Hydrodynamics. Busan, Korea:NSH, 2003. |
| [8] | LIU D C, HONG F W, ZHAO F, et al. The CFD analysis of pro-peller sheet cavitation[C]//Proceedings of the 8th international conference on hydrodynamics, ICHD-2008. Nantes, France:ICHD, 2008. |
| [9] |
刘登成, 洪方文, 张志荣, 等. 螺旋桨片状空泡的CFD分析[J]. 舰船科学技术 , 2009, 31 (1) :43–46.
LIU Deng-cheng, HONG Fang-wen, ZHANG Zhi-rong, et al. The CFD analysis of propeller sheet cavitation[J]. Ship Science and Technology , 2009, 31 (1) :43–46. |
 2016, Vol. 38
2016, Vol. 38
