船舶辐射噪声主要由螺旋桨噪声、机械噪声、水动力噪声组成。在这三大噪声源中,螺旋桨噪声占很大的比例[1-3]。朱锡清等[4]研究了利用湍流谱和 FW-H 方程获得低频宽带噪声级的方法,但必需已知湍流场中脉动均方值与湍流相关长度,使得该预报方法具有较大局限性。熊鹰等[5-7]通过采用面元法计算非定常力,用力与声级的关系换算出低频离散谱噪声,求解螺旋桨随机连续力,换算出低频连续谱噪声,用模型试验方法外推得到高频谱形成了螺旋桨噪声预报方法,该方法很大程度上依赖于模型试验和相关输入参数选取。王永生等[8]通过建立实尺度“船-桨”系统数值模型,结合 CFD 软件与 Virtual-lab,对螺旋桨噪声进行了研究但该方法需要计算资源和计算周期过大,工程应用难度较大。
随着 CFD 技术的发展,可使用数值方法来计算船体表面的外部流场[9-10]。然后根据 Lighthill 的声类比理论把声场计算与流场计算结合在一起,通过求解流场信息进而求解流噪声。本文主要对螺旋桨的非空泡噪声进行数值计算研究,以大涡模拟(LES)理论计算获取螺旋桨旋转过程中形成的湍流脉动信息,然后将其流场可导入 Actran 进行声场计算。并通过相关的试验数据验证该数值计算方法的计算精度。
1 基本理论本文螺旋桨噪声数值模拟的基础理论是莱特希尔(Lighthill)提出的声类比理论,Lighthill 首次将声场计算与流场计算结合在一起,通过求解流场信息进而求解流噪声,为流噪声的研究奠定了基础。随后柯尔(Curle)用基尔霍夫方法将 Lighthill 理论推广到考虑静止固体边界的影响。结果表明,固体边界的作用相当于在整个固体边界上分布偶极子,且每点偶极子的强度等于固体表面该点作用在流体上力的大小。Ffowcs-Williams 和 Hawkings 应用广义函数法将柯尔的结果扩展到考虑运动固体边界对声音的影响,即物体在流体中运动的发声问题,得到一个较为普遍的结果–福茨威廉姆-霍金斯方程(简称 FW-H 方程)。
当采用 Lighthill 方程或广义的 Lighthill 方程来计算声场辐射时,统称为声学比拟方法。通过整理连续方程和动量方程,并简化得到远离湍流区域流体中的均质声学波动方程[11-12]:
| $\frac{1}{a_{0}^{2}}\frac{{{\partial }^{2}}\rho '}{\partial {{t}^{2}}}-{{\nabla }^{2}}\rho \text{ }\!\!'\!\!\text{ }=0,$ | (1) |
通过 N-S 方程,可得到连续方程和动量方程:
| $\begin{align} & \frac{\partial \rho }{\partial \tau }+\frac{\partial \rho u{{\text{ }\!\!'\!\!\text{ }}_{i}}}{\partial y{{'}_{i}}}=0, \\ & \frac{\partial \rho u{{\text{ }\!\!'\!\!\text{ }}_{i}}}{\partial \tau }+\frac{\partial \rho u{{\text{ }\!\!'\!\!\text{ }}_{i}}u{{\text{ }\!\!'\!\!\text{ }}_{j}}}{\partial y{{'}_{i}}}=\frac{\partial \rho }{\partial y{{'}_{i}}}+\frac{\partial {{e}_{ij}}}{\partial y{{'}_{j}}}, \\ \end{align}$ | (2) |
进一步推导,可得到密度波动方程:
| $\frac{{{\partial }^{2}}\rho '}{\partial {{t}^{2}}}-a_{0}^{2}{{\nabla }^{2}}\rho \text{ }\!\!'\!\!\text{ }=\frac{\partial {{T}_{ij}}}{\partial {{x}_{i}}\partial {{x}_{j}}}\text{。}$ | (3) |
其中,Tij 为应力张量;a0 为等熵条件下的声速值;ρ' = ρ - ρ0(ρ 与 ρ'分别为扰动与未扰动时的密度)为声传播引起介质密度的变化。
2 预报模型 2.1 流场计算模型将螺旋桨桨叶模型导入模型建立软件(Gamit、Patran 或 Icem-CFD),为了使计算流场可满足计算等效,螺旋桨噪声数值模拟流场计算原则如下:
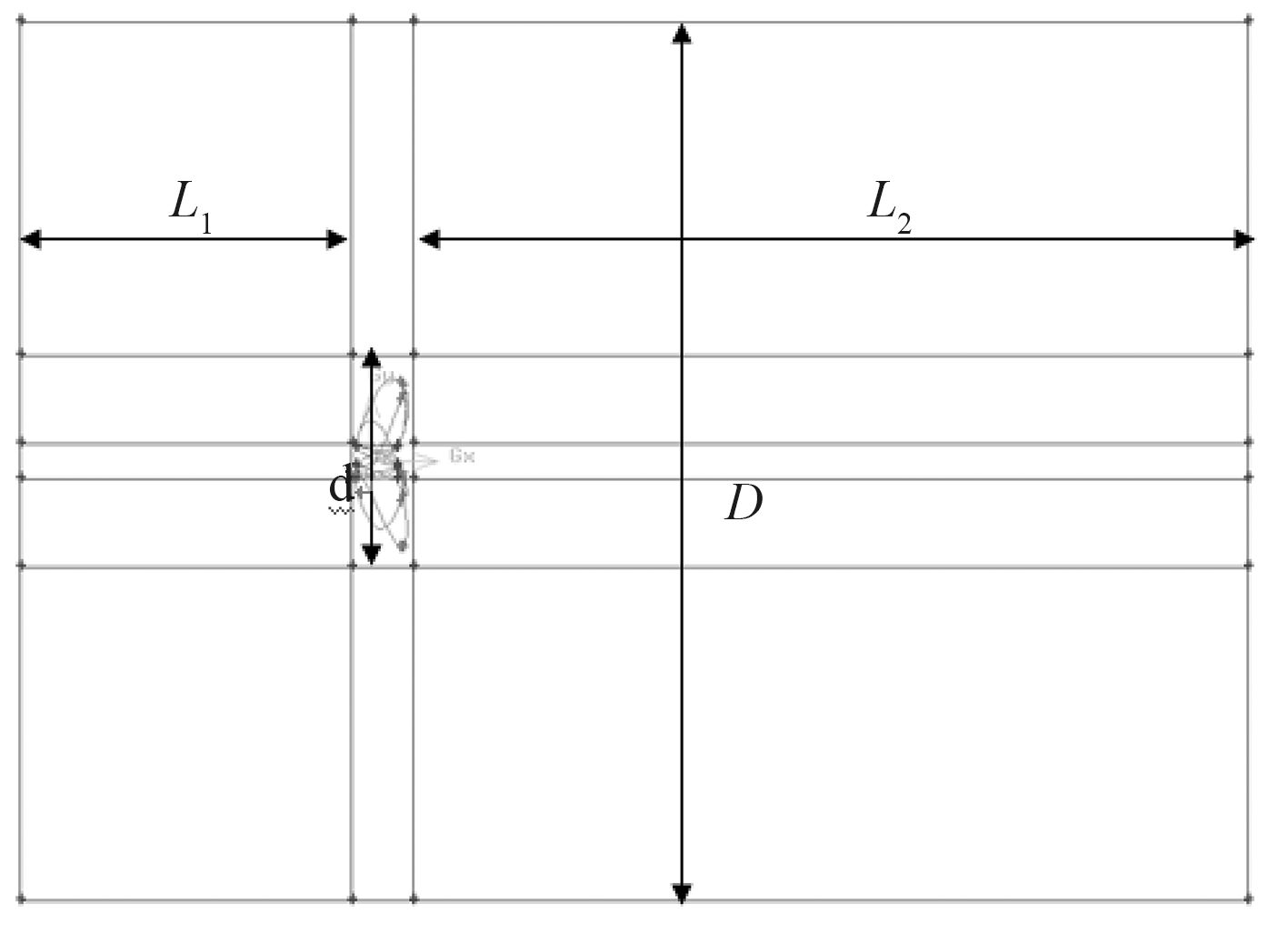
1)来流入口到螺旋桨距离 L1 ≥ 2 d;
2)模型直径 D1 ≥ 6 d;
3)模型流场出口距螺旋桨距离 L2 ≥ 5 d;
4)设置专门的螺旋桨旋转区,该区域紧贴螺旋桨旋转区域建立,各表面与螺旋桨桨叶之间距离 0.1 d ≥ △d ≥ 0.05 d。
如图 1 所示,流域划分为 11 个区域分别设置网格。其中,d 为螺旋桨直径,D1 为圆柱模型直径,△d 为旋转区域各表面与螺旋桨桨叶之间距离。
|
图 1 流场计算区域划分 Fig. 1 The flow field count area is divided |
在划分网格时,为了既能控制网格节点的数目又能捕捉到重要的流场信息,采用尺度函数对网格进行局部加密,在流动变化剧烈的叶根、叶梢、导边及随边附近进行了网格加密处理,体网格由螺旋桨表面区域向外域增大尺度,尺度增长比率控制在 1.2 以内以保证网格变化的平滑。螺旋桨旋转区域采用非结构网格,余下流域为规则模型,采用结构网格划分。
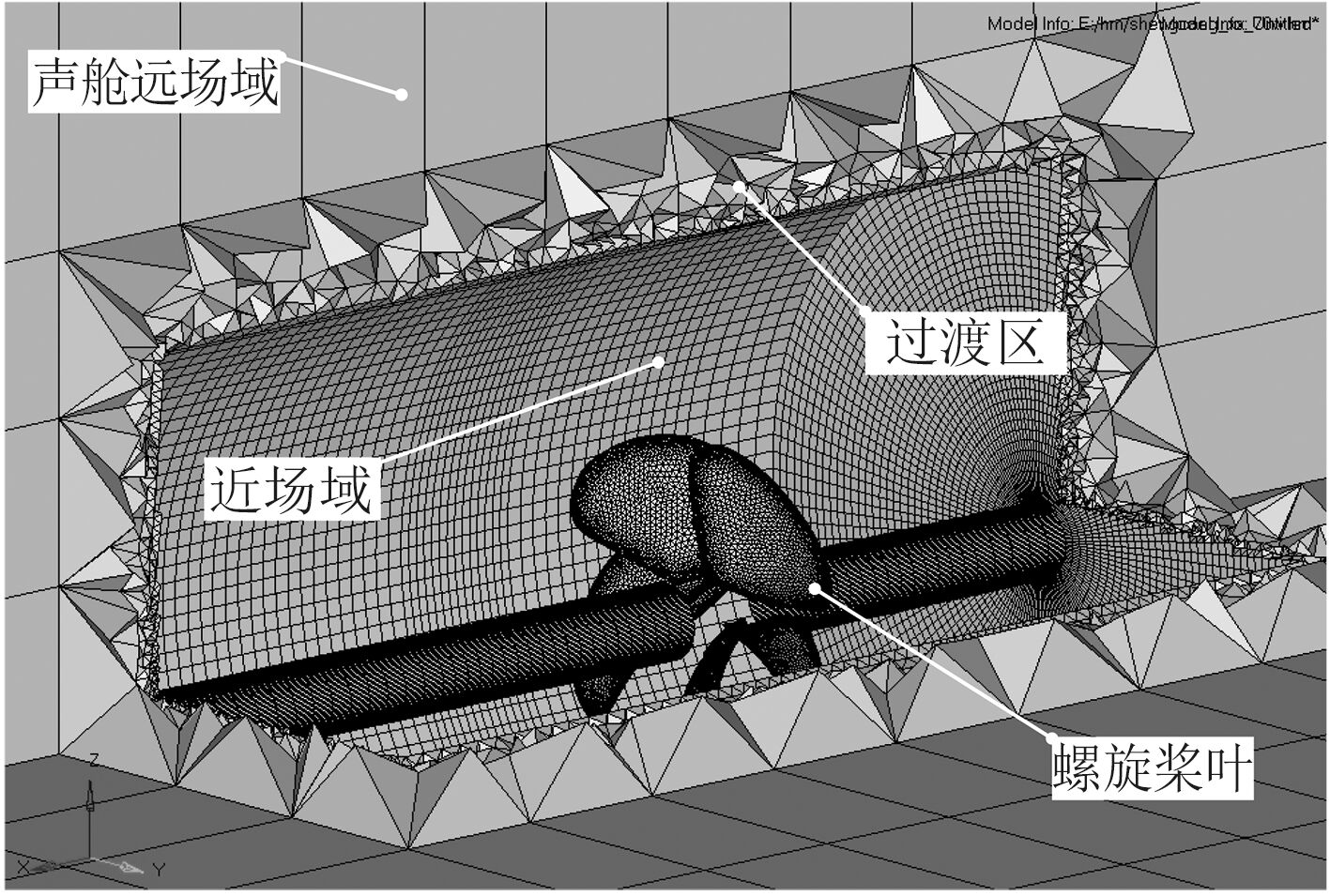
2.2 声学计算模型将流场计算模型导入声学模型建模软件,根据声学计算模型需要,建立包括面声源域、体声源域和声传播区域。根据后期声源提取需要,计算模型的外部尺寸和流场计算旋转区域与声学模型面声源保持一致;根据计算需要,设置体声源等效区域,设置原则为直径 D2 ≥ 1.5 d,来流 L3 ≥ 1 d ,流出方向 L4 ≥ 1.5 d。结构如图 2 所示。

|
图 2 声学计算区域划分 Fig. 2 The acoustics count area is divided |
相比流场计算网格,声学计算网格划分中不存在动网格,即螺旋桨桨叶及转区域网格,需要进行网格化分的区域均为规则几何体,均可以采用六面体网格划分,面声源和体声源区域,由于需要捕捉流场计算涡信息,需要对网格进行加密,最好与流场计算模型中网格保持一致。声场传播区域,根据声学计算需要,网格密度由计算频率确定,网格尺寸应满足小于计算频段内最小波长 1/6 要求,如计算频率为 5 000 Hz 时,网格尺寸应小于 0.05 m。
2.3 流场计算以某民用船舶螺旋桨为研究对象,完成其噪声预报分析。流场计算应用 Fluent LES 大涡模计算模块完成,其主要目的是捕捉湍流涡时域信息,以满足后期声学计算需要。在完成流场计算模型和网格化以后,计算流场信息的准确与否将取决于边界条件设置。
为了确保流场计算信息的准确性,在流场计算结束,对螺旋桨推力系数和扭矩系数进行计算,与试验值进行对比,判断流场计算结果的正确性。
为模拟非均匀伴流场的影响,计算模型边界条件采用试验测量得到的伴流场。在非均匀来流条件下,计算收敛后,通过提取螺旋桨在轴线上受力 T 及力矩 Q。应用以下公式可计算螺旋桨的相关系数:
推力系数${K_T} = \displaystyle \frac{T}{{\rho {n^2}{D^4}}}$;
扭矩系数 ${K_Q} = \displaystyle \frac{Q}{{\rho {n^2}{D^5}}}$。
其中:ρ 为水的密度;D 为螺旋桨直径;n 为螺旋桨转速。
模型流场计算结果如图 4 所示。
|
图 3 计算网格模型 Fig. 3 Calculation grid pattern |

|
图 4 螺旋桨流场 Fig. 4 Propeller neighbouring flow field |
螺旋桨噪声数值模拟利用信息为螺旋桨旋转形成的湍流脉动压力信息,其获取方式为利用 lighthill 声比拟理论,提取螺旋桨旋转区域表面压力信息,构成面声源。
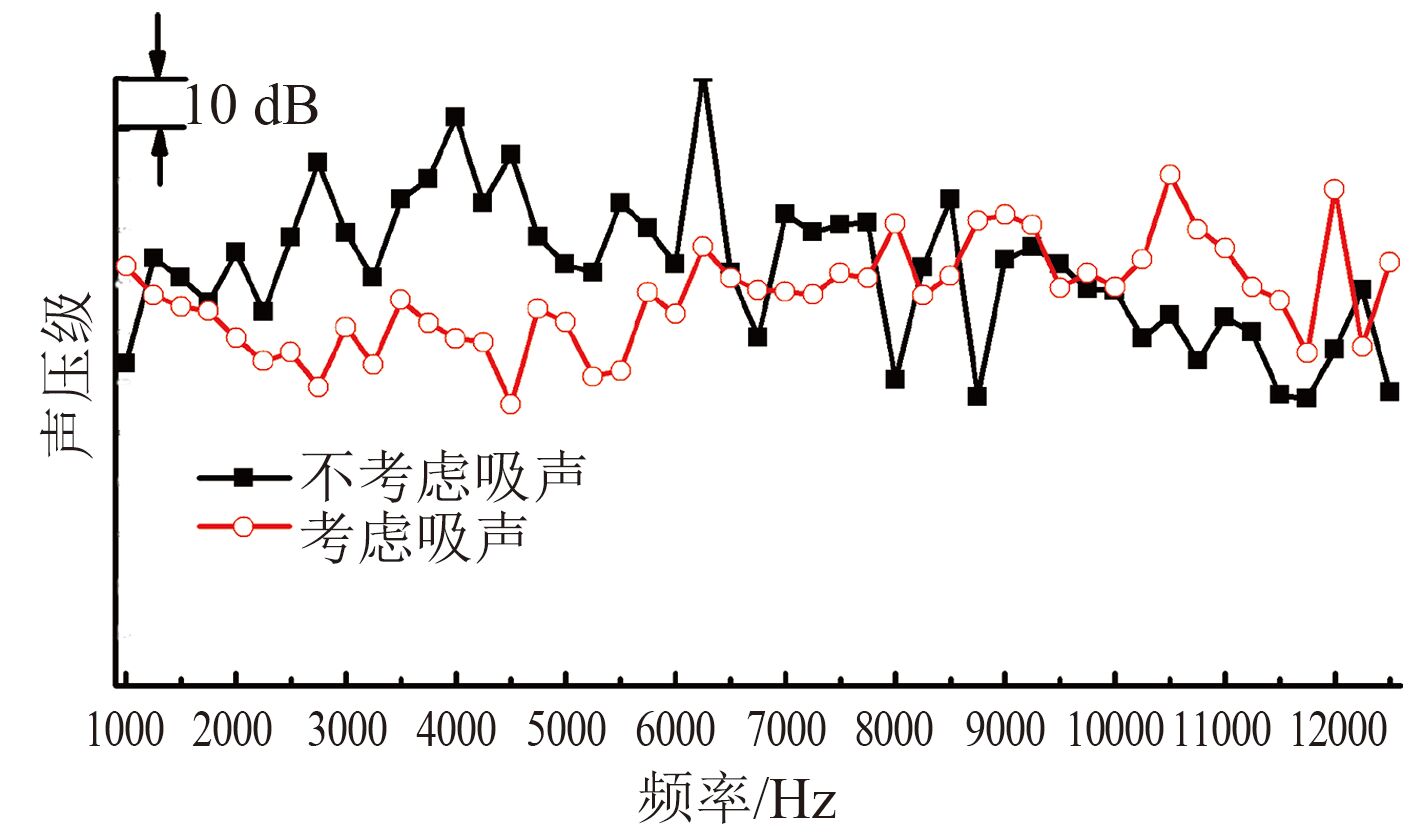
为研究边界条件对计算结果的影响,建立 2 种边界条件模型。对 2 种计算结果进行对比,结果如图 5 所示。由图可知,反射边界会产生混响声场,声压曲线波动幅度大,无反射边界得出的声压值变化相对平缓。
|
图 5 两种边界声压级频谱对比 Fig. 5 Sound pressure level frequency notes comparing for tow boundary condition |
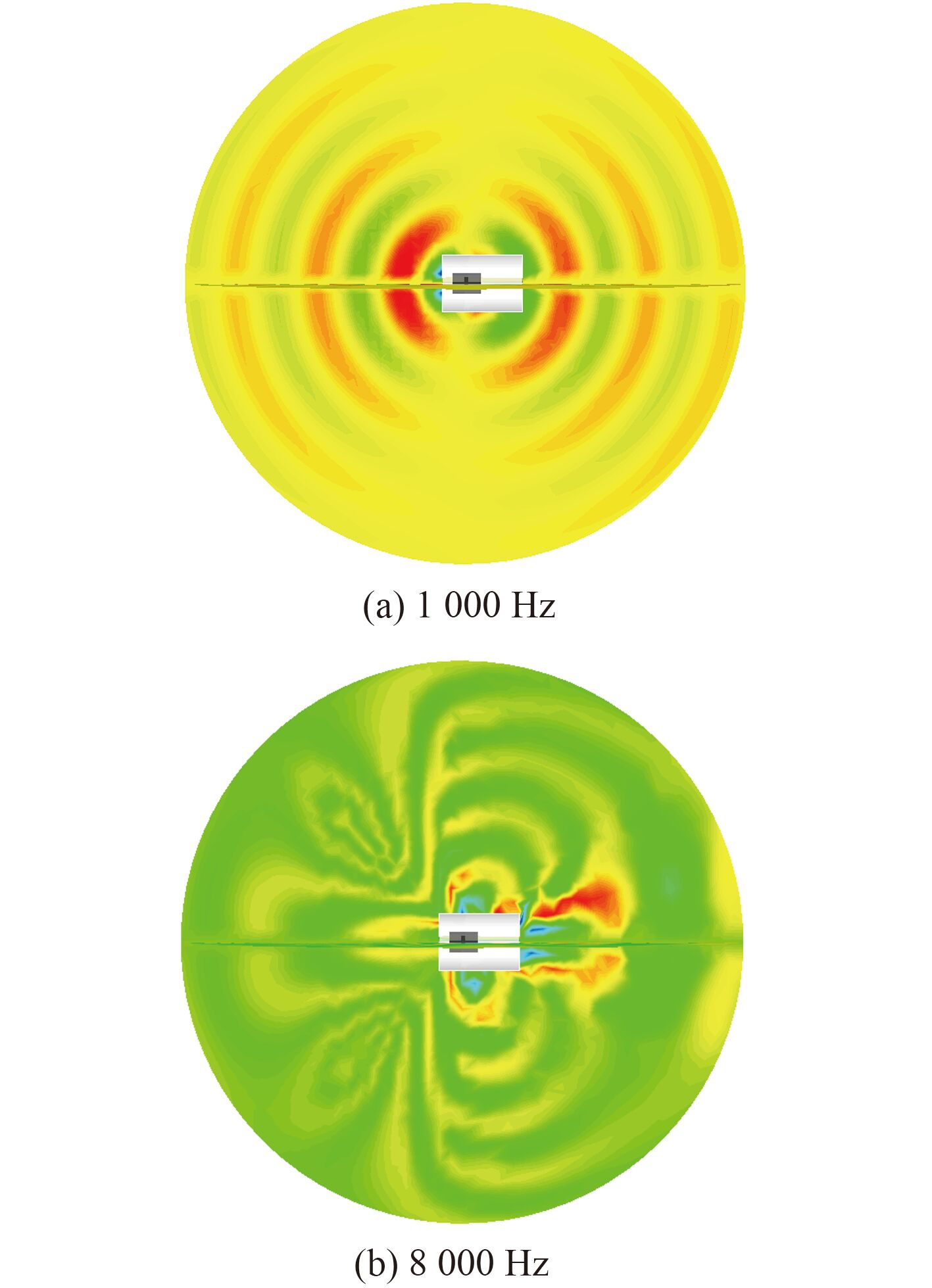
为了对螺旋桨产生的远场声辐射特性进行研究,建立远场声辐射模型如图 6 所示。该模型等效体声源部分与声舱计算模型保持一致,分别在 x,y,z 轴向设置远场测量面,并且在半径 5 m 处均匀设置测量点。图 7 给出了螺旋桨声压空间分布云图,图 8 给出螺旋桨声压空间分布云图和指向性图。可以看出,螺旋桨辐射噪声在不同频率均存在一定空间指向性,并且在不同频率上指向性也存在差异。

|
图 6 远场声辐射计算模型 Fig. 6 Distance field radiation of sound computation module computational mode |
|
图 7 声压分布指向性云图 Fig. 7 Sound pressure distribution directivity cloud chart |
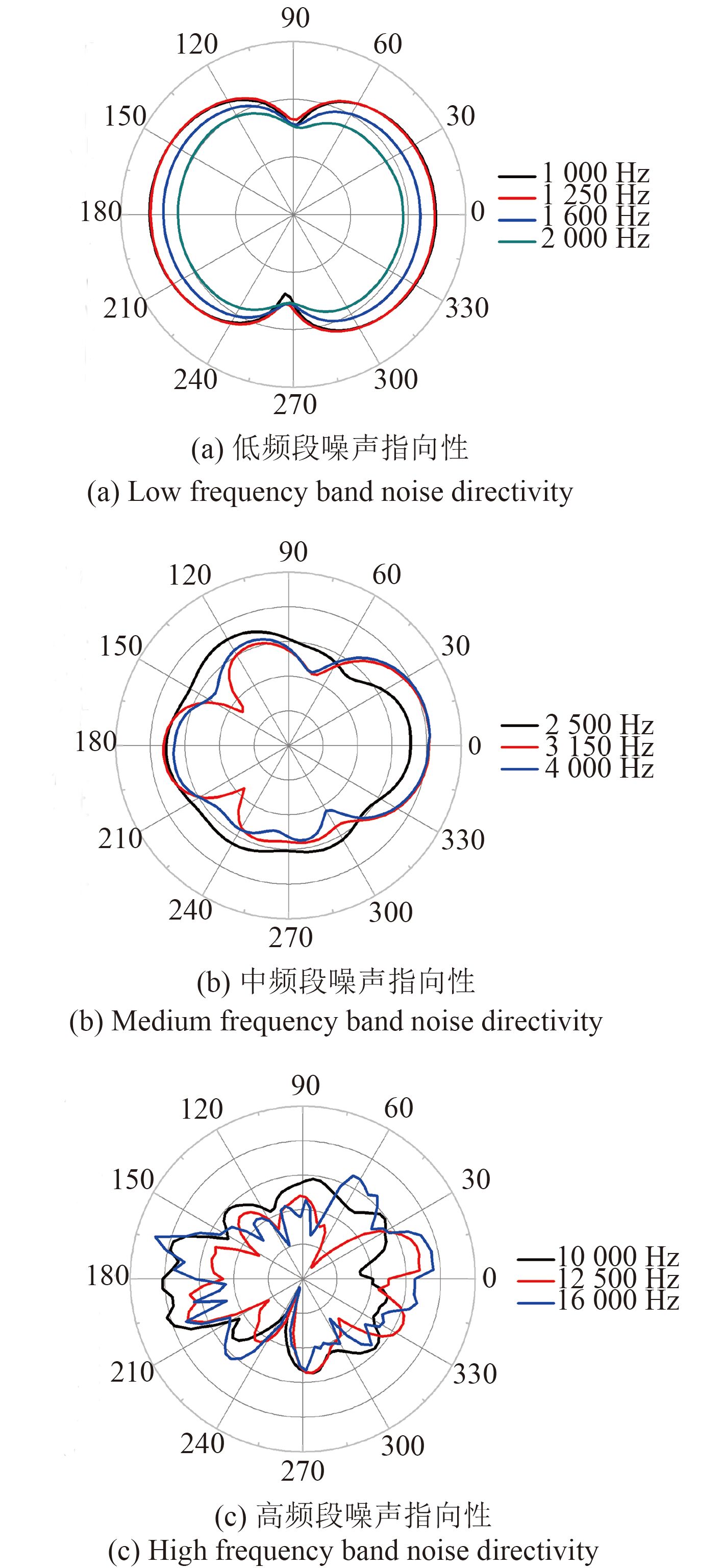
|
图 8 螺旋桨噪声指向性 Fig. 8 The propeller noise directivity |
图 8(a)中噪声在 0° 与 180° 方向最大,所示该方向为桨轴方向,而在垂直于桨轴方向,螺旋桨盘面所在位置为最小值。低频段噪声指向性关于桨轴和盘面呈对称分布。相关文献同样有桨叶数为单数的螺旋桨其低频噪声指向性呈对称分布的结论[3]。由图 8(b)可看出,中频段螺旋桨噪声指向性呈非对称分布,在迎流方向声压值小,被流方向声压值最大;由图 8(c)可看出,高频段螺旋桨噪声分布无明显规律,呈放射状分布。
3 计算精度为验证本研究方法的有效性,对预报结果中 1 m 测量点处声压级进行提取,统一声压的参考量级后,与试验结果进行对比,对比结果如图 9 所示。可以看出,在 1~12.5 kHz 范围内,数值预报结果无论从声压级和趋势上,均与试验数据保持了较好的一致性。各频率处声压级误差最大 7.56%,最小 0.89%,计算频段内总声级计算值与试验值误差小于 2 dB。由此可以得出本文计算方法对于非空化螺旋桨的噪声预报有较高的计算精度。由于本文方法采用有限元计算,受计算条件和效率的影响,所能计算的频率范围有限,对于螺旋桨的高频噪声预报较困难。因为螺旋桨噪声在超高频部分呈现明显的下降趋势对于螺旋桨噪声所关心的频率[13-14],该方法已经基本能满足噪声分析需求。
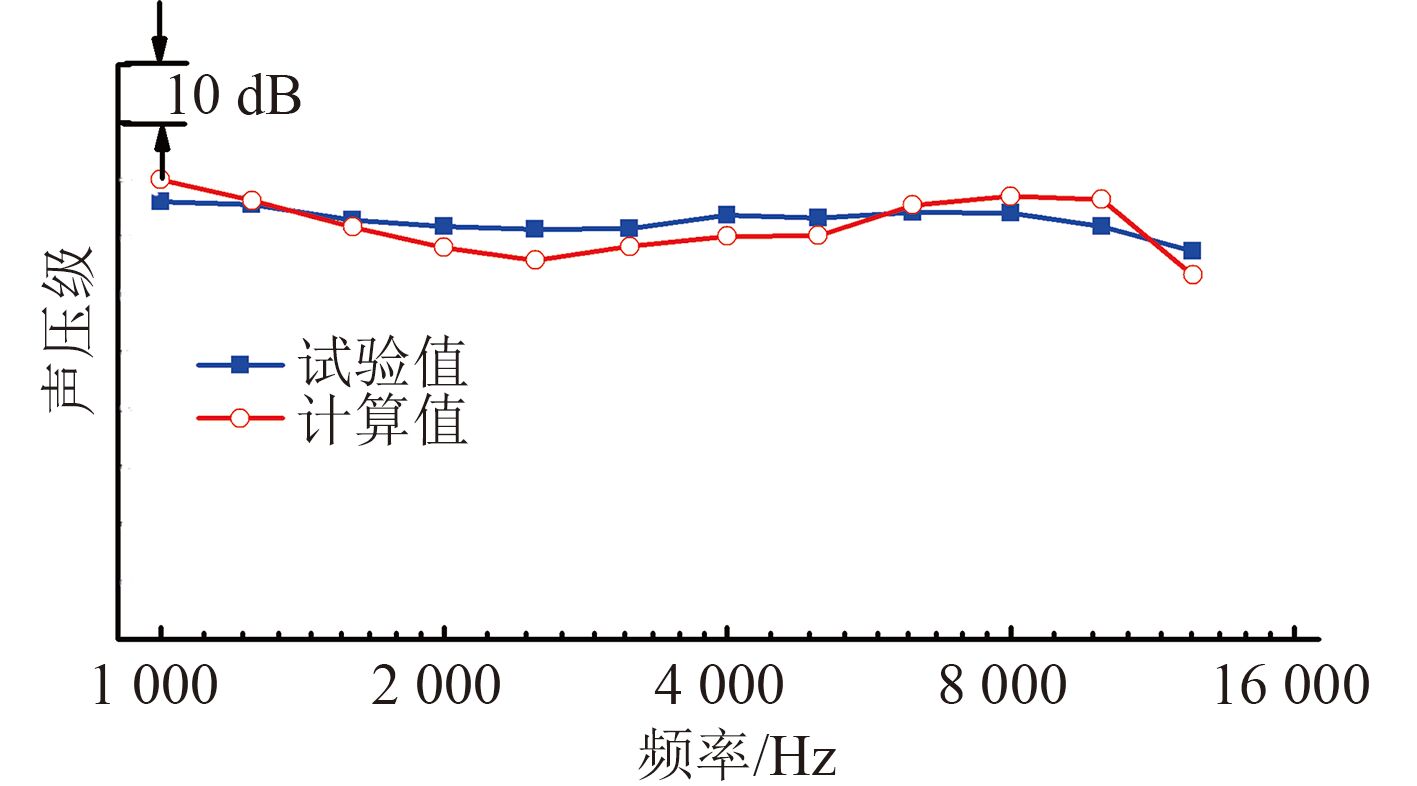
|
图 9 数值预报结果与试验数据对比 Fig. 9 The numeric predictet data compares against the test |
本文根据 Lighthill 的声类比理论把声场计算与流场计算结合在一起,通过大涡模拟得到螺旋桨流场信息,对流程信息进行提取、变化、传递得到螺旋桨的噪声分布规律与辐射特性。研究得到如下结论:
1)对于五叶桨,其低频噪声指向性呈对称性分布,轴向最大,盘面方向最小;
2)中频段噪声指向性呈非对称分布,在迎流方向声压值小,被流方向声压值最大;
3)高频段噪声分布无明显规律,呈放射状分布;
4)在 1~12.5 kHz 范围内,计算值与试验值在各频率处声压级误差最大 7.56%,最小 0.89%,计算频段内总声级计算值与试验值误差小于 2 dB。
| [1] |
熊紫英, 朱锡清, 刘小龙, 等. 船尾伴流场-导管-螺旋桨互作第38卷张成,等:螺旋桨非空泡噪声数值计算方法研究用噪声预报研究[J]. 声学学报 , 2009, 34 (2) :117–123.
XIONG Zi-ying, ZHU Xi-qing, LIU Xiao-long, et al. Stern wake-duct-propeller interaction noise prediction and research[J]. Acta Acustica , 2009, 34 (2) :117–123. |
| [2] |
杨琼方, 王永生, 张志宏. 非均匀进流对螺旋桨空化水动力性能的影响[J]. 水动力研究与进展 , 2011, 26 (5) :538–550.
YANG Qiong-fang, WANG Yong-sheng, ZHANG Zhi-hong. Effects of non-uniform inflow on propeller cavitation hydro-dynamics[J]. Chinese Journal of Hydrodynamics , 2011, 26 (5) :538–550. |
| [3] |
谢剑波, 周其斗. 非均匀流场中螺旋桨线谱噪声指向性分析[J]. 中国舰船研究 , 2010, 5 (6) :6–11.
XIE Jian-bo, ZHOU Qi-dou. Directivity prediction on tone noise of propeller operating in non-uniform flows[J]. Chinese Journal of Ship Research , 2010, 5 (6) :6–11. |
| [4] |
孙红星, 朱锡清. 螺旋桨离散谱噪声计算研究[J]. 船舶力学 , 2003, 7 (4) :105–109.
SUN Hong-xing, ZHU Xi-qing. Study on discrete noise induced by marine propeller[J]. Journal of Ship Mechanics , 2003, 7 (4) :105–109. |
| [5] |
张永坤, 熊鹰, 赵小龙. 螺旋桨无空泡噪声预报[J]. 噪声与振动控制 , 2008, 28 (1) :44–47.
ZHANG Yong-kun, XIONG Ying, ZHAO Xiao-long. Prediction of propeller non-cavitations noise[J]. Noise and Vibration Control , 2008, 28 (1) :44–47. |
| [6] |
张永坤, 况贶. 螺旋桨噪声的无量纲化研究[J]. 舰船科学技术 , 2007, 29 (2) :65–68.
ZHANG Yong-kun, KUANG Kuang. Research of propeller noise non-dimensionalization[J]. Ship Science and Technology , 2007, 29 (2) :65–68. |
| [7] |
张永坤, 熊鹰. 基于面元法及模型试验的船舶螺旋桨噪声预报方法[J]. 武汉理工大学学报(交通科学与工程版) , 2008, 32 (5) :818–821.
ZHANG Yong-kun, XIONG Ying. Prediction of ship pro-peller noise using surface panel method and experimental investigations[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering) , 2008, 32 (5) :818–821. |
| [8] |
杨琼方, 王永生, 曾文德, 等. 大侧斜螺旋桨负载噪声的边界元数值声学方法频域内计算分析[J]. 兵工学报 , 2011, 32 (9) :1118–1125.
YANG Qiong-fang, WANG Yong-sheng, ZENG Wen-de, et al. Calculation of highly-skewed propeller's load noise using BEM numerical acoustics method in frequency domain[J]. Acta Armamentarii , 2011, 32 (9) :1118–1125. |
| [9] |
高富东, 潘存云, 蔡汶珊, 等. 基于CFD的螺旋桨敞水性能数值分析与验证[J]. 机械工程学报 , 2010, 46 (8) :133–139.
GAO Fu-dong, PAN Cun-yun, CAI Wen-shan, et al. Numeric-al analysis and validation of propeller open-water performance based on CFD[J]. Journal of Mechanical Engineering , 2010, 46 (8) :133–139. DOI:10.3901/JME.2010.08.133 |
| [10] |
韦喜忠, 黄振宇, 洪方文. 基于非结构网格的螺旋桨周围流场大涡模拟[J]. 水动力研究与进展 , 2008, 23 (4) :419–425.
WEI Xi-zhong, HUANG Zhen-yu, HONG Fang-wen. Large eddy simulation of flowfield about marine propeller on unstructured meshes[J]. Chinese journal of Hydrodynamics , 2008, 23 (4) :419–425. |
| [11] |
龚京风, 张文平, 明平剑, 等. 螺旋桨低频流噪声模拟方法研究[J]. 中国舰船研究 , 2012, 7 (5) :14–21.
GONG Jing-feng, ZHANG Wen-ping, MING Ping-jian, et al. Numerical analysis of the propeller low frequency flow-noise[J]. Chinese Journal of Ship Research , 2012, 7 (5) :14–21. |
| [12] | SEOL H, JUNG B, SUH J C, et al. Prediction of non-cavitating underwater propeller noise[J]. Journal of Sound and Vibration , 2002, 257 (1) :131–156. DOI:10.1006/jsvi.2002.5035 |
| [13] |
王波, 张永坤, 高霄鹏. 基于模型试验的螺旋桨空泡噪声计算[J]. 海军工程大学学报 , 2010, 22 (6) :87–90.
WANG Bo, ZHANG Yong-kun, GAO Xiao-peng. Calculation of ship propeller cavitation noise based on model experiment[J]. Journal of Naval University of Engineering , 2010, 22 (6) :87–90. |
| [14] |
谢剑波, 周其斗, 纪刚, 等. 均匀流场中螺旋桨线谱噪声的频域预报方法[J]. 哈尔滨工程大学学报 , 2010, 31 (5) :585–588.
XIE Jian-bo, ZHOU Qi-dou, JI Gang, et al. Frequency-domain method for predicting the tone of noise from a propeller operating in uniform flows[J]. Journal of Harbin Engineering University , 2010, 31 (5) :585–588. |
 2016, Vol. 38
2016, Vol. 38
