2. 中国船舶重工集团公司第七〇四研究所, 上海 200031
2. The 704 Research Institute of CSIC, Shanghai 200031, China
随着船舶技术的发展,船载设备的种类及功能得到进一步完善,这在极大程度上丰富了船舶的适用范围,提升了船舶作为一个高集成度的一体化载体的智能化程度。然而不可否认,随着船载设备所涉传感器/执行器数量的增多,船舶各系统内及系统间所需传递的数据信息数量不断增加,这在极大程度上加重了各系统的通信负担,也增大了其通信线路的铺设难度。与此同时,船舶一体化平台对各系统信息进行综合分析、处理及决策的客观需求,也促使船舶框架研究人员对船舶各系统的通信线路进行整合,进而衍生出其在船舶信息系统(Ship Information System,SIS)领域的研究。不失普遍性,船舶信息系统架构可概括为命令控制接口(Command Control Interface,CCI)及其与全船层面上各传感器/执行器间进行数据传输的通信网络[1]。目前比较常见并已应用到实船上的船舶信息系统包括RICE[2],Ship System 2000[3],GEDMS[4]及TSCE[5]等。在文献[6]中,本文作者曾对行业内船舶信息系统领域近十几年的发展及研究成果进行概述并对其内涵进行了定义与说明。对于一个大规模的船舶信息系统,隶属于不同传感器节点的多个传感器需要进行高精度的再次融合。然而目前的研究仍是以船载独立系统为对象进行研究,其均在一定程度上忽略了船舶信息系统自身的客观属性,对通信网络所能承受的信息负载能力考虑不足。
在最近几年中,美国海军研究实验室已开发出一款名为“Volume Sensor”[9]的多感官实时检测系统,该系统可作为各种实时传感和情景应用模板。在此基础上,文献[10]中Christian等将该系统应用于船舶火灾探测系统上,并将基于信息的通信协议引入到一个模块化、可扩展的船舶传感器网络系统中。文献[11, 12]中本文作者结合已有系统完成了对船舶信息系统的常见框架及体系结构的建立,但并没有对其数据流通信过程开展深入研究。
由于船舶信息系统所挂传感器/执行器均隶属于不同系统,各系统对信息实时性的要求程度不同,如何在节约系统资源情况下,最大限度的将必要信息采集、发布成为了船舶信息系统研发过程中急需考虑的问题。当前一般将其归结为任务决策层面,其中比较有代表性的决策方法包括TSCE的ISP(Integrated Ship Plan)。该方法实现了全船层面下的船舶任务及指令优先级设定,并依此对船舶各个系统进行实时规范。该方法有效提升了船舶信息系统的监控效率和可靠性。然而,考虑到船舶信息系统的特异性和复杂性,在规范数据流长度的情况下,各节点在一个通信周期内仅能发布/获取部分必需信息,因而增加了数据流内容分配的必要性。为此,文献[13]通过对船舶信息系统能达性进行分析,并在充分考虑执行器物理特性的情况下,提出了一种行之有效的船舶信息系统执行器通道设定方案,但是其理想化了执行器及通信网络之间的通信过程,因而有一定的局限性。
为解决上述问题,本文对船舶信息系统数据流设定问题开展研究,在能达性/能观性基础上,提出了船舶信息系统数据流长度判据,并分别提出了对执行器节点及传感器节点的数据流内容的设定方案。在缩短数据流长度的前提下,保证了系统对数据信息采集、处理及应用的客观需求,进而优化了系统资源、提升了系统性能。
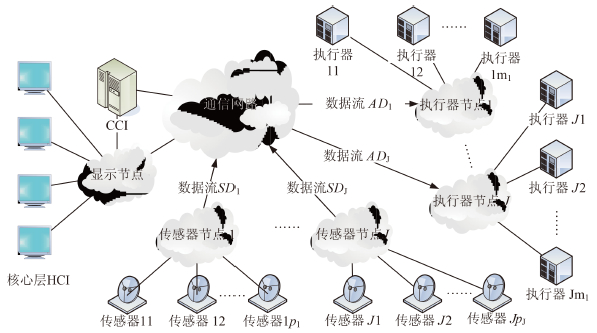
1 船舶信息系统框架不失一般性,本文采用如图 1所示的船舶信息系统典型框架。各电子系统内的被控对象表示为Q=[Q1,…QJ]。为忽略无关因素,本文假设船舶信息系统所涉所有底层自身对象$ {Q_j} \in{Q} $均具备能控性/能观性。Qj的状态方程如下:
| $ {{x}_{j}}(k+1)={A_j}{{x}_{j}}(k)+{B_j}{{u}_{j}}(k)\text{,}\\ {{y}_{j}}(k)={C_j}{{x}_{j}}(k)\text{。} $ | (1) |
|
图 1 船舶信息系统典型框架 Fig. 1 Typical structure of SIS |
1)执行器节点、传感器节点及显示器节点彼此完全独立。
2)对于单一被控对象,其所需的所有传感器信息均由一个传感器节点提供,其所涉执行器也均连接在一个执行器节点上,节点协同问题将作为今后的一个研究方向开展。与Qj相关的传感器节点表示为SNj,其数据流用SDj表示;执行器节点表示为ANj其数据流用ADj表示。
3)各数据流具备统一的通信标准,即不同节点的数据流长度相同。
4)传感器节点SNj一次仅能将$ {w_j}_\sigma $个传感器信息录入数据流中,且有$ 1 \leqslant {w_j}_\sigma \leqslant {p_j} $,即CCI在一次通信中仅能从SNj处获取有限的数据信息。执行器节点一次仅能获取$ {w_j}_\rho $个执行器控制指令,且有$1 \leqslant {w_j}_\rho \leqslant {m_j} $。
1.1 选取队列对于i=1,2…,pj,采用二值函数$ {\sigma _j}_{\rm{i}}(k)$表示其传感器Sij在k时刻被添加近数据流SDj的状态,即$ {\sigma _j}_{\rm{i}}(k):Z \mapsto \{ 0,1\} $。其中“1”表示信息被添加如数据流,“0”表示未被添加。本文中,作者采用一种$ {p_j}{\rm{-}}to{\rm{-}}{w_j}_\sigma $选取队列$ {{\sigma }_{j}}(k){\rm{=[}}{\sigma _j}_1(k),\cdot \cdot \cdot,{\sigma _j}_{{p_j}}(k){]^{\rm{T}}} $被控对象所涉pj个传感器信息被添加如SDj情况。毫无疑问,SDj的数据长度完全取决于$ {w_j}_\sigma $的数值大小。
定义1 M-to-N选取队列为一个映射 $ {\sigma }(k): $ $ {Z^+} \mapsto {\{ 0,1\} ^M} $其满足$ {\left\| {{\sigma }(k)} \right\|^2}{\rm{=}}N,\forall k $。且该映射的矩阵形式为$ {{ M}_\rho }(k)\buildrel \Delta \over={\rm diag}({\sigma }(k))$。
就传感器Sji而言,其输出yji(k)能被船舶信息系统应用的先决条件是其信息被添加入数据流SDj并被信息系统采纳,即$ {\sigma _j}_i=1 $。否则船舶信息系统将视该传感器信息不可用,此时其数据信息将由估计值$ {\hat y_{ji}}(k)$代替,其确定方法将在后续章节进行阐述与分析。船舶信息系统在k时刻所真实采用的Sji信息表示为$ {\bar y_{ji}}(k)$,且有:
$$ {\overline y _{ji}}(k)={\sigma _j}_i(k)\cdot {y_{ji}}(k){\rm{+[1-}}{\sigma _j}_i(k)] \cdot {\hat y_{ji}}(k)\text{。} $$给定一个选择队列${\sigma _j}_{\rm{i}}(k)$,本文定义其矩阵形式为${{{M}}_j}_\sigma(k)$,且${{{M}}_j}_\sigma(k)\buildrel \Delta \over=diag({{\sigma }_{j}}(k))$,则有:
| $ {\overline {y} _{j}}(k)={{{M}}_j}_\sigma(k)\cdot {{y}_{j}}(k){\rm{+[}}{{\rm{I}}_{{p_j}}}{\rm{-}}{{{M}}_j}_\sigma(k)] \cdot {{\hat y}_{j}}(k)\text{。} $ | (2) |
其中${\overline {y} _{j}}(k)={[{\bar y_{j1}}{\rm{,}} \cdot \cdot \cdot {\rm{,}}{\bar y_{j{p_j}}}]^{\rm{T}}},{{\hat y}_{j}}(k)={[{\hat y_{j1}}{\rm{,}} \cdot \cdot \cdot {\rm{,}}{\hat y_{j{p_j}}}]^{\rm{T}}} $
采用${{\rho }_{j}}(k){\rm{=[}}{\rho _j}_1(k),\cdot \cdot \cdot,{\rho _j}_{{m_j}}(k){]^{\rm{T}}} $表述执行器Aji能否获取有效的控制指令,且有${{{M}}_{j\rho }}(k)\buildrel \Delta \over={\rm diag}({{\rho }_{j}}(k))$。假设船舶信息系统运算出的控制指令表示为${\overline{u} _j}{\rm{=[}}\overline {{u_j}_1},\cdot \cdot \cdot,\overline {{u_j}_m} {]^{\rm{T}}} $,则有:
| $ {{u}_{j}}(k){\rm{=}}{{{M}}_j}_\rho(k){\overline {u} _{j}}(k)\text{。} $ | (3) |
结合式(2)和式(3),式(1)可拓展为如下表达形式:
| $ {{x}_{j}}(k+1)={A_j}{{x}_{j}}(k)+{B_j}{{{M}}_j}_\rho(k){\overline {u} _{j}}(k)\text{,}\\ {\overline {y} _{j}}(k)={{{M}}_j}_\sigma(k)\cdot {C_j}{{x}_{j}}(k){\rm{+[}}{{\rm{I}}_{{p_j}}}{\rm{-}}{{{M}}_j}_\sigma(k)] \cdot {{{\hat y}}_{j}}(k)\text{。} $ | (4) |
定义2 对于给定的选取队列${{\sigma }_{j}}(k)$,根据[k0,kf]时刻上的${\overline {y} _{j}}(k)$能够唯一确定系统在k0的初始状态x(k0),则称称被控对象(4)在[k0,kf]区间能观测。若存在一个正整数l,使得对于任何k,对象(4)在区间[k,k+l]能观测,则称对象(4)为l步可观测。
定义3 对于给定的选取队列ρj(k),若对于任意xf,均存在一个控制信号$\overline{u}(k)$使得被控对象(4)满足从x(k0)=0到x(kf)=xf,则称被控对象(4)在[k0,kf]能达。若存在一个正整数l,使得对于任何k,对象(4)在区间[k,k+l]能达,则称对象(4)为l步能达。
为此本文所解决的问题可概括为:
1)确定${w_{\sigma j}}$及${w_{\rho j}}$数值使得被控对象Qj满足loj步能观测及lrj步能达;
2)提出合适的调度算法以从pj传感器中挑选${w_{\sigma j}}$个传感器并将其数据添加入传感器数据流;
3)提出合适的选取方法以从mj执行器中挑选${w_{\rho j}}$个执行器控制指令,并将其添加入执行器数据流。
2 数据流长度设计首先开展对对象(4)能观性的分析,并将其拓展到能达性分析过程。为考虑传感器选取问题对系统能观性的影响,首先假设${{\hat y}_{j}}(k){\rm{=}}0$。可证明,当且仅当rank(R)=nj时,被控对象(4)在[0,kf]可观,其中:
| ${ R}{\rm{=}}\left[{\begin{array}{*{20}{c}} {{M_j}_\sigma(0){C_j}}\\ {{M_j}_\sigma(1){C_j}{A_j}}\\ \vdots \\ {{M_j}_\sigma({k_f}-1){C_j}A_j^{{k_f}-1}}\text{。} \end{array}} \right]\text{。} $ | (5) |
在每一步k,${{ M}_j}_\sigma(k)$可从每一个CjAjk中挑选出${w_j}_\sigma $行。可证当${{ M}_j}_\sigma(k)$选出的${k_f} \cdot {w_j}_\sigma $项包含nj个线性无关项时,rank(R)=nj。其证明过程如下:
定理1 假设Aj(k)可逆,将kf表示为kf=α×nj+β,其中$\alpha \in N$,β=1,…,nj-1。如果${w_j}_\rho$满足如下条件之一,则被控对象(4)在[0,kf]能观测。
① ${w_j}_\sigma \le \beta {\rm{且}}{w_j}_\sigma \ge \left\lceil {{n_j}/(\alpha + 1)} \right\rceil {\rm{ }} $
② $ {w_j}_\sigma > \beta {\rm{且}}{w_j}_\sigma \ge \left\lceil {\left( {{n_j} - \beta } \right)/(\alpha )} \right\rceil $,此时α需为正整数。
证明:取${\varGamma _{ji}} \buildrel \Delta \over={[{C_j}A_j^{{n_j}i},{C_j}A_j^{{n_j}i+1},\cdot \cdot \cdot,{C_j}A_j^{{n_j}i+{n_j}-1}]^{\rm{T}}}$,由于Aj可逆且(1)能观,可证对于所有$i \in N$矩阵${\varGamma _{ji}}$秩为nj。取$\gamma _{ji}^0,\cdot \cdot \cdot,\gamma _{ji}^{{n_j}-1}$为${\varGamma _{ji}}$内的任意nj个线性无关项,且用Lji表示集合$\{ \gamma _{ji}^0,\cdot \cdot \cdot,\gamma _{ji}^{{n_j}-1}\} $。考虑如下方法:
①取Lj=Lj0;
②用Lj1内的${w_j}_\rho$行替代Lj内的${[\gamma _{j0}^{{w_j}_\sigma {\rm{+}}1},\gamma _{j0}^{{w_j}_\sigma {\rm{+}}2},\cdot \cdot \cdot \gamma _{j0}^{{w_j}_\sigma {\rm{+}}{n_j}-1}]^{\rm{T}}}$并保证rank=Lj(nj),由于rank=Lj(nj),该种替代方法可时刻成立
③对于i=2,…,用Lji内的${w_j}_\rho$行替代Lj内的${[\gamma _{j0}^{i \times {w_j}_\sigma+1},\gamma _{j0}^{i \times {w_j}_\sigma+2},\cdot \cdot \cdot,\gamma _{j0}^{i \times {w_j}_\sigma+{w_j}_\sigma }]^{\rm{T}}}$,并时刻保持rank=(Lj)nj
上述替代方法的结果是Lj均包含来自${\varGamma _{ji}}$内的${w_j}_\sigma$且保证rank=Lj(nj)。该方法即可在每个${{ \varGamma} _{ji}}$中选取${w_j}_\sigma$行的情况下选取nj个线性无关项。基于上述方法,可重构R的右端为${[{M_j}_\sigma(0){C_j},{M_j}_\sigma(1){C_j}{A_j},]}$ ${[\cdots {M_j}_\sigma(\alpha \times {n_j}+\beta -1){C_j}A_j^{\alpha \times {n_j}+\beta -1}]^{\rm{T}}}$ 。进而可从${[{C_j}A_j^{{n_j} \times(\alpha -\alpha)+\beta -1},\cdot \cdot \cdot,{C_j}A_j^{{n_j} \times \alpha+\beta -1}]^{\rm{T}}}$选取$\alpha \times {w_j}_\sigma$个线性无关项。在此之后,若$[{C_j},\cdot \cdot \cdot,{C_j}A_j^{\beta -1}]$处获取另外${w_j}_\sigma$个线性无关项,为此总共可选取的线性无关项数量为$(\alpha+1)\times {w_j}_\sigma$,由此可见当$(\alpha+1)\times {w_j}_\sigma \geqslant {n_j}$时,被控对象(4)在[0,kf]上可观。另一方面若${w_j}_\sigma > \beta$,$[{C_j},\cdot \cdot \cdot,{C_j}A_j^{\beta -1}]$处尽可获取β个线性无关项,为此所能选取的线性无关项总数为$\alpha \times {w_j}_\sigma+\beta $,由此可见当$\alpha \times {w_j}_\sigma+\beta \geqslant {n_j}$时,被控对象(4)在[0,kf]上可观。
为降低船舶信息系统冗余程度并节约数据流资源,本文选取满足条件A或B的最小${w_j}_\sigma$为添加入每个数据流SDj中的传感器数量。
推论1 假定Aj可逆且(1)能观,存在可确定的整数${w_j}_\sigma$,用以构建一个选取队列${\sigma _j}(\cdot)$来保证被控对象(4)对于给定的整数loj,loj步能观测。
证明:根据定理1,可知存在整数${w_j}_\sigma$及选取队列${{\rho }_j}(\cdot)$使得被控对象(4)在$[0,\alpha \times {n_j}+\beta]$能观测。队列Mjcp(k)可从矩阵${{{C}}_j}{{A}}_j^{\alpha \times {n_j}+\beta -k-1}(k=0,\cdot \cdot \cdot,\alpha \times {n_j}+$ $ \beta -1)$ 选取nj个线性无关项。参照文献[14]可证,对任何${l_{oj}} \geqslant 2N-1$,选取队列${M_j}_\sigma(k)$可以在[i,i+loi]周期性的选取nj个线性无关项,使得对于任意i,被控对象(4)在${{\sigma }_j}(k)$下loj步能观测。假设N=α×nj+β。可证对于给定的loj,可找到${w_j}_\sigma$在满足条件A和B的条件下,保证被控对象(4)loj步能观测。
结合定理1及推论1可证,存在可确定的整数${w_j}_\rho$,用以构建一个选取队列${\rho _j}(\cdot)$来保证被控对象(4)对于给定的整数lcj,lcj步能达。
3 数据流内容设计 3.1 执行器数据流内容设计基于上述推论,对于给定lcj步能达对象(4),可推算出其执行器数据流长度所需添加的控制指令${w_j}_\rho$数量,进而确定数据流长度。接下来本文通过考虑执行器物理特性提出了船舶信息系统执行器数据流内容的取舍标准。为此须以执行器实时工作情况为指标将船舶信息系统执行器定义KⅠ类(“倔强”)执行器及KⅡ类(“依从”)执行器。
定义4. 对于执行器Aji,若其在k时刻仍处于执行前次控制指令阶段,而忽视当前控制指令uji(k),则称Aji在k时刻为KⅠ类(“倔强”)执行器,反之则为KⅡ类(“依从”)执行器。对任意正常工作Aji而言,若其处于待机(无可执行控制指令)阶段,则其必为KⅡ类。
结合图 1,可知当且仅当如下条件之一成立时,执行器Aji在k时刻为KⅠ类。
① Aji伺服系统存在缓存器,且被设定为在完成前条指令前,忽视所有当前指令;
② CCI将控制指令uji(k)添加入ADj,但被ANj屏蔽,未发送到Aji;
③ CCI未将控制指令uji(k)添加入ADj。
条件①情况下为Aji主动KⅠ类,②和③情况下为被动KⅠ类。为节约系统资源,本文所提出的船舶信息系统数据流设定方案,将条件③作为KⅠ类的实施方法。可知,在执行器数据流内容设定过程中,应尽量筛除针对KⅠ类的控制指令。根据SIS对Aji当前指令运行情况的掌控程度,KⅠ类的设定判据如下:
1)基本规则
若Aji当前指令运行情况不可知,则须设定物理属性变量${\chi _{ji}}(k-1,k)$,${g_{ji}}{({z_0},\lambda)_{\max }}$及${g_{ji}}{({z_0},\lambda)_{\min }}$,其定义如下:
| $ {\chi _{ji}}(k - 1,k) = \left\lceil {\tau ({u_{ji}}(k - 1) \to {u_{ji}}(k))/{\tau _0}} \right\rceil .$ | (6) |
其中$\tau({u_{ji}}(k-1)\to {u_{ji}}(k))$表示执行器Aji从uji(k-1)运行到uji(k)所需的物理时间,${\tau _0}$为SIS循环周期。z0为Aji的运行初始值。${g_{ji}}{({z_0},\lambda)_{\max }}$与${g_{ji}}{({z_0},\lambda)_{\min }}$分别表示$\lambda $个运行周期内,Aji所能运行到的最大、最小值。为此,KⅠ的基本设定规则为:
$$ \{ {A_j}_i \in {{\rm K}^{\rm I}}|{u_{ji}}(k+{r_{ji}})\notin [{g_{ji}}{({u_{ji}}(k),{r_{ji}})_{\min }},\\ {g_{ji}}{({u_{ji}}(k),{r_{ji}})_{\max }}]{\rm{\ }}{\chi _{ji}}(k-1,k)> 1\} \text{。} $$其中rji表示执行器从uji(k-1)运行到uji(k)状态所需的步数,且${r_{ji}} < {\chi _{ji}}(k-1,k)$。需要说明的是,当${A_j}_i \in {{ K}^{I}}$时,系统可视${\rho _j}_{\rm{i}}(k){\rm{=1}}$。
2)附加规则
在上述规则基础上,若Aji当前指令运行情况可知,其表示为${v_j}{\rm{=[}}{v_j}_1{\rm{,}} \cdot \cdot \cdot {\rm{,}}{v_j}_{{m_j}}{\rm{]}} \in {R^{{m_j}}}$,则有如下附加规则:
$$ \{ {A_j}_i \in {{ K}^{\rm I}}\left| {{{}_j}_i(k)\ne {u_j}_i(k-1)} \right.{\rm{\ sgn((}}{u_j}_i(k{\rm{-}}1)-\\[5pt] \quad\quad {v_j}_i(k))={\rm{sgn}}({u_j}_i(k)- {u_j}_i(k-1))\text{。} $$ 其中${\rm{sgn((}}{u_j}_i(k{\rm{-}}1)- {v_j}_i(k))={\rm{sgn}}({u_j}_i(k)- {u_j}_i(k-1))$表示Aji仍在运行之前的指令uji(k-1)。基于上述规则,船舶信息系统执行器数据流内容的添加原则为优先添加KⅡ类执行器的控制指令,若其数量小于${w_j}_\rho$则添加面向KⅠ的控制指令,但其指令内容维持为上次输入值,相似的方法可参照文献[13]。
3.2 传感器数据流内容设计提出了一种基于双指标评价方法的传感器数据信息的选取方案。
1)传感器变值指标
对于i=1,…,pj,采用二值函数${\delta _j}_{\rm{i}}(k)$表示传感器Sji的变量指标。当且仅当$\left| {{y_{ji}}(k)- {y_{ji}}({k_{\eta ji}})} \right| > {\varepsilon _{ji}}$时,${\delta _{ji}}(k)=1$。其中${y_{ji}}({k_{\eta ji}})$表示传感器Sji上一次获取权限添加入数据流SDj中的传感器信息。${\varepsilon _{ji}}$为阈值,表示当传感器所示数值变量超过阈值时,其变量指标${\delta _j}_{\rm{i}}(k)$为1,否则为0。当${\delta _j}_{\rm{i}}(k){\rm{=}}1$时,本文将Sji标记为${\Theta _j}$类传感器。且有${{\delta }_{j}}(k)\!=\! [{\delta _{j1}}(k),\cdots,{\delta _{j{p_j}}}(k)]$。传感器变量指标由各传感器节点确定。与此同时,本文定义${\eta _{ji}}(k)=k-{k_{\eta ji}}$,且${{\eta }_{j}}=[{\eta _{j1}}(k),\cdots {\eta _{j{p_j}}}(k)]$。
2)传感器偏差指标
对于i=1,…,pj,采用二值函数${\phi _j}_{\rm{i}}(k)$表示传感器Sji的偏差指标,其取值由传感器Sji的${\bar y_{ji}}(k-1)$与${\hat y_{ji}}(k-1)$的差值确定。当且仅当$\left| {{{\bar y}_{ji}}(k \!-\! 1)- {{\hat y}_{ji}}(k \!-\! 1)} \right| > {\varphi _{ji}}$时,有${\phi _j}_{\rm{i}}(k)=1$。其中${\hat y_{ji}}(k-1)$是CCI对于${y_{ji}}(k-1)$的估计值。${\varphi _{ji}}$为阈值,其表示当上次CCI实际采用的Sji数值与其估计量的差值若大于${\varphi _{ji}}$,则其在k步的偏差指标${\phi _j}_{\rm{i}}(k){\rm{=}}1$,否则为0。由于篇幅有限,本文将不对传感器信息最优估计方法进行赘述,可参照作者之前的研究成果[15]。传感器偏差指标由CCI确定,并且通过信息读取指令SCj(k)发送到SNj。
3)传感器信息调度方法
基于上述双评价指标,提出一种传感器信息调度方法。为此,定义优先级函数${\Xi _{ji}}(k){\rm{=}}{\phi _j}_{\rm{i}}(k{\rm{-}}{\eta _{ji}})+{\phi _j}_{\rm{i}}(k{\rm{-}}{\eta _{ji}}+1)+\cdots {\phi _j}_{\rm{i}}(k)$,其数值大小决定了CCI对传感器Sji的需求程度。当CCI获取到来自Sji信息时,${\Xi _{ji}}(k)$重置为0。信息读取指令SNj为如定义1结构的${p_j}{\rm{-}}to{\rm{-}}{w_j}_\sigma$选择队列,且有${{\lambda }_{j}}(k){\rm{=[}}{\lambda _j}_1(k),\cdot \cdot \cdot,{\lambda _j}_{{p_j}}(k)]$。本文选出优先级函数${\Xi _{ji}}(k)$数值较大的${w_j}_\sigma$个传感器,并设定${\lambda _j}_i(k)=1$,否则为0。若Sji所对应的${\lambda _j}_i(k)=1$,则称该传感器为${\Lambda _j}$类传感器。
当传感器节点SNj从CCI获取SCj(k),${{\sigma }_{j}}(k)$可由${{\eta }_{j}}(k),{{\lambda }_{j}}(k),{{\delta }_{j}}(k)$及另一队列${{\psi }_{j}}(k)$确定。其中${{\psi }_{j}}(k){\rm{=[}}{\psi _{j1}}(k),\cdot \cdot \cdot,{\psi _j}_{{p_j}}(k)]$,且满足$\{ {\psi _{ji}}(k)=1\left| {{\lambda _{ji}}\cdot} \right.$ ${(k-1)=1,\sigma _{ji}}(k-1)=0\} $ ,否则${\psi _{ji}}(k)=0 $。即,当CCI在k-1步发布了针对传感器Sji的采集指令,但该信息未被节点添加入SDj中时,${\psi _{ji}}(k)=1$。为此,本文将此类传感器标记为${\Phi _j}$类传感器。定义如下4类传感器工作情况,即
$$ {S_{ij}} \in {{\rm{\gamma }}_j},{\rm{iff}}{S_j}_i \in {\Lambda _j} \cap {\Theta _j};\\[5pt] {S_j}_i \in \Omega _j^{\rm I},{\rm{if}}{S_j}_i \in {\Lambda _j}{\rm{but}}{S_j}_i \notin {\Theta _j};\\[5pt] {S_j}_i \in \Omega _j^{{\rm I}{\rm I}},{\rm{if}}{S_j}_i \notin {\Lambda _j}{\rm{but}}{S_j}_i \in {\Theta _j}\\[5pt] {S_j}_i \in \Omega _j^{{\rm I}{\rm I}{\rm I}},{\rm{if}}{S_j}_i \in {\Phi _j}{\rm{and}}{S_j}_i \in {\Theta _j} $$本文所提出的传感器数据流信息调度方法如下:
①当${\lambda _j}_i(k)=1$时,预设${\sigma _{ji}}(k)=1$。这表示${\varUpsilon _j}$及$\Omega _j^{\rm I}$获取上传数据信息的优先权限。
②将$\Omega _j^{\rm I}$的权限转移至$\Omega _j^{{\rm I}{\rm I}}$,其顺序取决于nji(k)数值大小,移次数取决于$\Omega _j^{\rm I}$与$\Omega _j^{{\rm I}{\rm I}}$的最小值。需要说明的在权限转移过程中,$\Omega _j^{{\rm I}{\rm I}{\rm I}}$类传感器的权限最高,且不受其nji(k)值大小的限制。
③重建${{\sigma }_{j}}(k)$。基于${{\sigma }_{j}}(k)$将相应传感器信息添加入SDj,与此同时也应将其最终的选取队列${{\sigma }_{j}}(k)$添加入SDj作为CCI确定信息类型的依据。根据${{\sigma }_{j}}(k)$重设${{\eta }_{j}},{{\psi }_{j}}(k)$。
4 例 证以1艘中型船舶的运动控制任务为例,对上文提出的船舶信息系统数据流设计方案进行阐述。该系统执行器包括双舵(包含舵鳍)、双桨及一对减摇鳍(包含翼鳍),系统状态空间方程形式为${{\dot x}_1} \!\!=\!\! f({{x}_1},{{u}_1})$,其状态量包括 ${{x}_1} \!\!=\!\! {[{\psi _s},{\dot \psi _s},{\phi _s},{\dot \phi _s},{V_s},{\dot V_s}]^{\rm{T}}}$,其中V、$\psi$及$\phi$分别表示船舶航速、航向及横摇。由于篇幅有限,船舶运动模型及控制策略的研究可参照作者之前的研究成果[11,12],其执行器包括${{u}_1}={[{\delta _{R{\rm{-}}Lm}},{\delta _{R{\rm{-}}Lf}},{\delta _{R{\rm{-}}Rm}},{\delta _{R{\rm{-}}Rf}},}$ $ {{\eta _{F{\rm{-}}m}},{\eta _{F{\rm{-}}f}},{\nu _{P{\rm{-}}L}},{\nu _{P{\rm{-}}R}}]^{\rm{T}}}$ 其中$R{\rm{-}}Lm,R{\rm{-}}Lf,R{\rm{-}}Rm,$$R{\rm{-}}Rf,F{\rm{-}}m,F{\rm{-}}f$分别表示左主/翼舵、右主/翼舵、主/翼鳍及左右桨,仅在上式中${\delta _ \cdot },{\eta _ \cdot },{\nu _ \cdot }$分别表示舵角、鳍角及螺旋桨转速。
假设系统Q1需满足15步能达,且起始时刻为k0,为此执行器数据流设定方法为:根据推论1,可设kf=7;由于kf=αn1+β,n1=6,则可知α=1,β=1;基于章节2所述定理及推论可知,${w_{j\rho }}{\rm{=}}5$,即表示:若当每个执行器流中至少包括5个执行器的控制指令,则系统可满足15步能达,在此过程中每个KⅡ执行器具备相同获取控制指令的权限,且均高于KⅠ执行器权限。
基于同样的被控系统,假定其包含8个须被采集传感器,即${{y}_1}={[{\psi _s},{\dot \phi _s},{V_s},{\theta _{R{\rm{-}}L}},{\theta _{R{\rm{-}}R}},{\theta _{F{\rm{-}}m}},{\nu _R},{\nu _L}]^{\rm T}}$,其中${\theta _{R{\rm{-}}L}},{\theta _{R{\rm{-}}R}},{\theta _{F{\rm{-}}m}},{\nu _R},{\nu _L}$分别表示左舵舵角、右舵舵角、鳍角及左右桨转速。在此假设系统需要25步能观。首先基于推论1,对于l1o=25,可设kf=13;由于kf=αn1+β且n1=6进而求出α=2、β=1;最后根据定理1,可知${k_f}{\rm{=13}}$,即表示:若当每个传感器数据流中至少包括5个传感器的相应数据,则系统可满足25步能观。进一步设定${{\eta }_{j}}(k)$,${{\lambda }_{j}}(k)$,${{\delta }_{j}}(k)$及${{\psi }_{j}}(k)$数值如下:
$$ {{\lambda }_{j}}(k)=\left\{ {1,1,1,1,0,0,0,0} \right\}\text{,}\\[3pt] {{\delta }_{j}}(k)=\left\{ {1,1,0,0,1,1,1,0} \right\}\text{,}\\[3pt] {{\eta }_{j}}(k)=\left\{ {0,0,1,0,2,3,4,0} \right\}\text{,}\\[3pt] {{\psi }_{j}}(k)=\left\{ {0,0,0,0,1,0,0,1} \right\}\text{。} $$可知,$\{ {S_j}_1,{S_j}_2\} \in {\Upsilon _j}$,$\{ {S_j}_3,{S_j}_4\} \in \varOmega _j^{\rm I}$,$\{ {S_j}_5,{S_j}_6,{S_j}_7\} \in \varOmega _j^{{\rm I}{\rm I}}$,$\{ {S_j}_5,{S_j}_8\} \in \varOmega _j^{{\rm I}{\rm I}{\rm I}}$。可知$\varOmega _j^{\rm I}$与$\varOmega _j^{{\rm I}{\rm I}}$的最小值为2,鉴于$\varOmega _j^{{\rm I}{\rm I}{\rm I}}$具备最高优先级,为此${\sigma _{j5}}(k)=1$。由于${\eta _{j7}}(k)> {\eta _{j6}}(k)$,因而Sj7获得通信权限。为此,在该例证中,传感器数据流的最终选择队列${{\sigma }_{j}}(k)=\{ 1,1,0,0,1,0,1,0\} $。
5 结 语在充分考虑系统能达性/能观性基础上,提出船舶信息系统数据流长度的普适判据,并分别提出面向执行器及传感器数据流内容的选取方法。从而完成了对船舶信息系数据流整体设计方案的研究,在缩短数据流长度的前提下,保证了系统对数据信息采集、处理及应用的客观需求,进而优化了系统资源、提升了系统性能,并为船舶信息系统的后续研究提供了理论基础。
| [1] | GEER D W. Total ship real time control:an operational necessity whose time has come[J]. Naval Engineers Journal, 1998, 110(1):225-234. |
| [2] | LISTER J R, ROSIE J D. A digital maritime integrated internal communication system[J]. Journal of Naval engineering, 1995, 35(3):504-519. |
| [3] | KLLBERG B, STRHLE R. Ship system 2000, a stable architecture under continuous evolution[C]//Proceedings of the 6th Ada-Europe International Conference on Reliable Software Technologies. Berlin Heidelberg:Springer, 2001:371-379. |
| [4] | MEIER S J, MANFREDI A. Gigabit ethernet data multiplex system (GEDMS)-enabling the net-centric evolution of navy combatants[C]//Proceedings of the 2006 IEEE Conference on Military Communications. Washington DC, USA:IEEE, 2006:1-7. |
| [5] | HENRY M, IACOVELLI M, THATCHER J. DDG-1000 engineering control system (ECS)[C]//Proceedings of the ASNE Intelligent Ship VⅢ Symposium. Philadelphia, USA:ASNE, 2009. |
| [6] | LIU S, XING B W, LI B, et al. Ship information system:overview and research trends[J]. International Journal of Naval Architecture and Ocean Engineering, 2014, 6(3):670-684. |
| [7] | LI Z X, YAN X P, GUO Z W, et al. A new intelligent fusion method of multi-dimensional sensors and its application to tribo-system fault diagnosis of marine diesel engines[J]. Tribology Letters, 2012, 47(1):1-15. |
| [8] | LIU S, WANG M J, ZHANG L Y. Research on information fusion of infrared and radar sensor based on SVM[C]//Proceedings of the 2012 International Conference on Measurement, Information and Control (MIC). Harbin, China:IEEE, 2012:98-101. |
| [9] | MINOR C P, JOHNSON K J, ROSE-PEHRSSON S L, et al. Data fusion with a multisensor system for damage control and situational awareness[C]//Proceedings of the 2007 IEEE Conference on Advanced Video and Signal Based Surveillance. London, UK:IEEE, 2007:313-317. |
| [10] | MINOR C, STEINHURST D, ROSE-PEHRSSON S, et al. Multisensor system for fire detection and situational awareness[R]. SPIE Newsroom, 2007. |
| [11] | LIU S, XING B W, LI B. Development actuality and key technology of networked control system[C]//Proceedings of the 32nd Chinese Control Conference. Xi'an, China:IEEE, 2013:6692-6697. |
| [12] | LIU S, XING B W, ZHI P F, et al. Design of semi-physical simulation platform for ship cooperative control system[C]//Proceedings of the 11th world congress on Intelligent Control and Automation (WCICA). Shenyang, China:IEEE, 2014:5962-5966. |
| [13] | XING B W, LIU S, ZHU W L. Actuator channel setting strategy for ship information systems based on reachability analysis and physical characteristic[C]//Proceedings of the 2015 IEEE 15th International Conference on Environment and electrical Engineering. Rome, Italy:IEEE, 2015:932-937. |
| [14] | ZHANG L, HRISTU-VARSAKELIS D. Communication and control co-design for networked control systems[J]. Automatica, 2006, 42(6):953-958. |
| [15] | LIU S, YANG D, Su X, et al. The vertical motion state estimation of hydrofoil catamaran based on improved UKF[C]//Proceedings of the 32nd Chinese Conference on Control Conference. Xi'an, China:IEEE, 2013:4618-4622. |
 2016, Vol. 38
2016, Vol. 38
