载人潜器非耐压框架结构是潜器各分系统设计安装的基础。作为潜器布放回收和母船系固的主要承力结构,耐压壳和设备的重量都要施加在承载框架上,框架结构设计需在满足刚度、强度以及局部稳定性规范的前提下,力求质量最小,同时还应考虑稳定性。本文基于多目标优化理论进行非耐压框架结构的优化设计,首先应用 APDL 建立框架结构的参数化模型,通过灵敏度分析选出设计变量,采用近似模型进行仿真计算。为节省材料,增大有效载荷以质量最轻为目标进行了单目标优化,在此基础上考虑结构稳定性,增加结构变形最小这一目标进行了多目标优化。
1 响应面近似模型技术响应面近似模型技术主要包含两方面:一是试验设计,其研究内容包括如何高效合理辨别关键设计因子,通过试验设计数据分析来最大化的获取信息;二是模型建立方法,研究如何进行数据拟合与构造预测模型[1]。
1.1 试验设计试验设计是数理统计的一个分支学科,它提供了合理快速获得所需数据信息的方法,提高了优化算法找寻最优解的速度。常用试验设计方法有:正交试验和最优拉丁超立方设计。正交设计是通过采用正交表来合理分析多因子试验的设计方法,具有效果好、收敛快、精确度高等特点[2]。最优拉丁超立方设计考虑到了随机拉丁超立方设计的均匀性缺陷,并在其基础上进行改进。
1.2 响应面近似模型响应面近似的本质是一种回归近似。通过采用数学函数拟合设计空间,求出待定系数从而确定近似模型,然后采用近似模型替代仿真模型,优势在于可以使用较少的样本点比较精准地逼近函数表达式[3]。其缺陷是不能保证响应面通过所有的样本点,因此会存在一定的拟合误差。响应面模型的多项式既可以为1阶也可以为2阶、3阶、4阶。设计因子的个数以及模型阶数对构建模型所需的样本点数有重要影响[4]。设a0,bi,cij,… 为近似函数逼近系数,近似函数响应面一般模型可以表示为:
| $ \tilde y(x) = {a_0} + \sum\limits_{i = 1}^m {{b_i}{x_i}} + \sum\limits_{ij(i < j)}^{} {{c_{ij}}{x_i}{x_j}} + \cdots \text{。} $ | (1) |
在初始设计方案的基础上,应用 Ansys 有限元软件的 APDL 脚本语言建立框架参数化模型。框架结构整体上可以分为首部、中部和尾部3部分。建模过程中,为了使有限元模型与实体模型尽量保持一致,框架中部的压载水舱、底部的基座以及首尾的横向板材用板单元建立,其他横向骨架和纵向骨架结构采用线单元建立,起吊环采用环形结构。结构相互连接的地方采用耦合连接方式以提高精度,将板架结构通过网格划分为规则的四边形,建模过程中通过对线单元赋予截面属性来反映其真实形状。通过对框架结构梁单元、面单元划分网格,框架模型一共有63个面,16 352个单元,23 031个节点。参数化有限元求解分析的全部数据包括参数化模型的建立、载荷的施加、网格自动划分、求解结果后处理及提取都应该用 APDL 语言进行编写形成一个输入文本文件,并对优化设计变量以参数化形式表示。
3 非耐压框架结构优化设计载人潜器非耐压框架结构的传统优化设计方法往往是单目标优化设计,即只追求单方面响应的优化而忽略了各目标间相互影响矛盾的因素,常常会导致产品的整体性能未必最优。本文将对多个子目标同时实施优化并考虑如何折中处理使问题达到某种意义下的最优。
3.1 多目标优化问题多目标优化即是同时对多个子目标进行优化,其数学表达式为:
| $ {\rm Minimize} \qquad{{f_m}(x)}\text{,} {\begin{array}{*{20}{c}} \quad {m = 1\text{,}2\text{,} \cdots M}\text{,} {} \end{array}}\\[4pt] {\rm S.T} \qquad {{g_j}(x) \leqslant 0}\text{,} \quad {j = 1\text{,}2\text{,} \cdots j}\text{,}\\[4pt] \qquad\qquad {{h_k}(x) = 0}\text{,} \quad {k = 1\text{,}2\text{,} \cdots K}\text{,}\\[4pt] \qquad\qquad {x_i^L \leqslant {x_i} \leqslant x_i^U}\text{,} \,{i = 1\text{,}2\text{,} \cdots ,n}\text{。} $ | (2) |
NSGA-Ⅱ 由 K. Ded,S. Agrawal 在2000年提出,是针对传统遗传算法的不足改进而来的,该算法很好解决了设计过程中最优解集与 Pareto 前沿距离较远的缺陷,使求解的非劣解集保持很高的多样性,现在已经发展为优化计算方法中的一种经典算法[5]。NSGA-Ⅱ 算法的关键之处在于引入了非劣分层排序和拥挤度距离2个概念,使NSGA-Ⅱ 算法的复杂度大大降低。通过改进适应度共享策略,省略了共享半径的指定过程,使算法的运行效率得到显著提高,优化解分布更加均匀,相对于其他优化算法表现优良[6]。
3.2 ISIGHT优化系统平台的建立Ansys 与 ISIGHT 的集成是整个优化设计的基础,也是关键性技术难点所在。一般可以通过2种方式实现集成操作,一种是 Ansys 专用组件,另一种是 Simcode 仿真组件[7]。Simcode 仿真组件集成相对 Ansys 组件不受 Ansys 软件版本的限制,集成操作灵活方便,因此本文采用 Simcode 仿真组件进行集成。Simcode 仿真组件是将输入、执行和输出操作进行集成的一个仿真组件,本质上包括 Input 属性页、Command 属性页和 Output 属性页3个部分。Simcode 工作流程如图 1 所示。
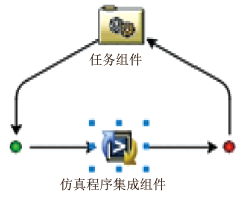
|
图 1 Simcode工作流程 Fig. 1 Simcode work flow |
本文优化计算流程是将 Ansys 与 ISIGHT 这2个软件集成,借助 ISIGHT 这一优化平台实现数值模型连续自动计算,这样极大减少了重复计算工作量,计算效率显著提高。优化工作流程如图 2 所示。
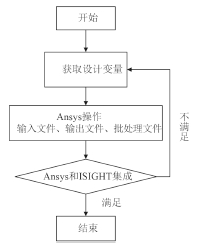
|
图 2 优化设计工作流程 Fig. 2 Optimization design work flow |
本文中潜器非耐压框架结构的优化对象主要是框架的纵向梁骨架、横向骨架构件、中部横向板架以及支座,它们是框架的主要承重构件,对框架强度支撑起重要作用。不影响框架强度分析的前提下,本文拟对框架结构进行简化处理,选取纵梁以及横肋骨工字梁的翼板厚度t1,翼板宽度w1,腹板厚度t3,腹板宽度w3,框架中部横舱壁板板厚tb这5个设计变量进行灵敏度分析,通过试验设计选取对目标函数值贡献大的优化变量作为优化设计变量。本次试验设计方法采用最优拉丁超立方设计的采样技术,样本点数设置为25。设计变量如图 3 所示,试验设计的主效应如图 4 所示。
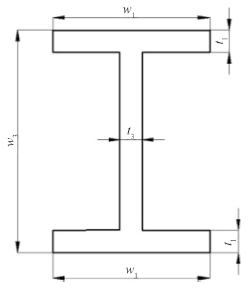
|
图 3 设计变量示意图 Fig. 3 Design variables schematic diagram |
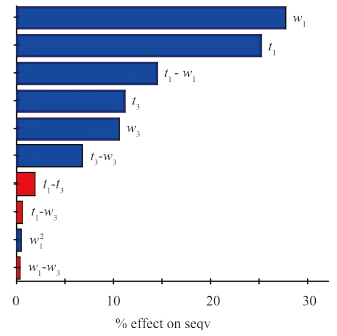
|
图 4 设计变量与最大应力灵敏度 Fig. 4 Design variables and maximum stress sensitivity |
考虑到设计框架结构时应首先保证最大应力满足要求,本文选取工字梁的翼板厚度t1,翼板宽度w1,腹板厚度t3,腹板宽度w3这4个设计变量进行参数化建模。
3.4 近似模型构建及精度分析应用试验设计方法构建框架结构近似模型,由试验设计得到目标函数值,通过二阶响应面技术进行拟合即可得到目标响应值与设计变量的2次多项式。响应面模型的拟合精度常用复相关系数的值来检验[8]。复相关系数R2 的定义如下:
| $ {R^2} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - \mathop {{y_i}}\limits^ \wedge )}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - y)}^2}} }}\text{。} $ | (3) |
| 表 1 近似模型精度检验表 Table 1 Approximation model accuracy test |
计算结果表明3个响应值的复相关系数皆为0.9以上,3个响应面的拟合度都较高,均达到了精度要求,满足工程计算需要。
3.5 单目标优化设计根据《潜水系统和潜水器入级与制造规范》中对潜器非耐压框架结构强度计算的有关规定,参考机械设计的相关要求,对框架结构进行优化设计。由前述设计变量的灵敏度分析可知工字梁的翼板厚度t1,翼板宽度w1,腹板厚度t3,腹板宽度w3这4个设计变量对框架结构重量、最大应力均有较大影响,故拟选取这4个设计变量作为优化变量,以最大应力作为约束,质量最小作为优化目标,整个优化模型如下所述:
$$ {\rm Minimize} \quad\quad {\rm weight}\\[4pt] {\rm s.t} \quad seqv \leqslant [{\sigma _s}]\\[4pt] {\rm DV}:\quad {t_1} = [6, 12]\text{;}\\[4pt] \quad\quad\quad {t_3} = [5, 10]\text{;}\\[4pt] \quad\quad\quad {w_1} = [60, 102]\text{;}\\[4pt] \quad\quad\quad {w_3} = [60, 150]\text{。} $$本文采用序列二次规划算法寻优。参数设置为:最大迭代次数为40、收敛精度为1.0 E-6、相对步长为1.0 E-4。优化迭代过程中的一些重要参数变化曲线如图 5~图 9 所示:
|
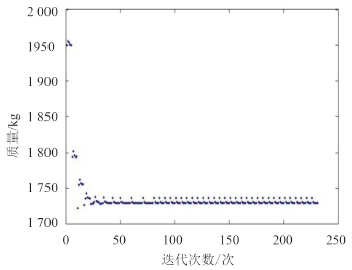
图 5 质量随迭代次数变化图 Fig. 5 Weight with the number of iterations |
|
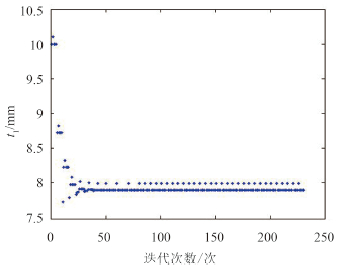
图 6 翼板厚度t1随迭代次数变化图 Fig. 6 Flap thickness with the number of iterations |
|
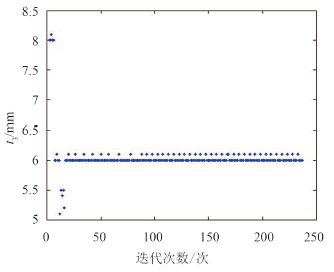
图 7 腹板厚度t3随迭代次数变化图 Fig. 7 Web thickness with the number of iterations |
|
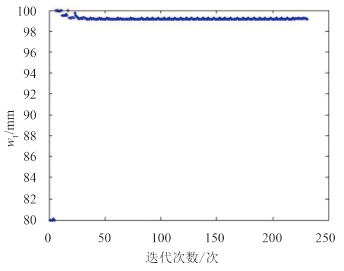
图 8 翼板宽度w1随迭代次数变化图 Fig. 8 Flap width with the number of iterations |
|
图 9 腹板宽度w3随迭代次数变化图 Fig. 9 Web width with the number of iterations |
质量在优化初期波动幅度较大,数值大小也比较分散,在之后的计算中框架结构重量的波动不显著,除少数质量出现较大跳跃之外,数值基本稳定在1 726 kg,较初始设计的1 949 kg 重量减轻了11.44%,为223 kg,优化效果明显。优化初期工字梁的4个设计变量均有较大变动,之后便基本稳定在某一数值左右,由图可知翼板厚度t1优化值为8 mm、翼板宽度w1优化值为99 mm、腹板厚度t3优化值为6 mm、腹板宽度w3优化值为60 mm。
3.6 多目标优化设计非耐压结构单目标优化结果表明框架的质量有所下降但最大位移却增加,这对框架的结构稳定性显然不利。为增强框架结构稳定性,对非耐压框架结构进行了多目标优化,选取框架质量最小和最大位移变小2个优化目标,数学模型如下:
$$ {\rm Minimize} \quad\quad {\rm weight}\\[3pt] {\rm Minimize} \quad\quad {\rm usum}\\[3pt] {\rm s.t} \quad seqv \leqslant [{\sigma _s}]\\[3pt] {\rm DV}: \quad {t_1} = [6\text{,}12]\text{;}\\[3pt] \quad\quad\quad {t_3} = [5\text{,}10]\text{;}\\[3pt] \quad\quad\quad {w_1} = [60\text{,}120]\text{;}\\[3pt] \quad\quad\quad {w_3} = [60\text{,}150]\text{。} $$| 表 2 单目标优化方案与初始方案比较 Table 2 Single-objective optimization result and initial design |
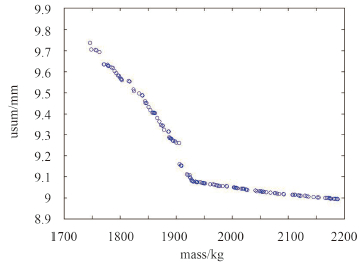
在上述集成多目标优化模型的基础上,选用 NSGA-Ⅱ 优化算法,设置种群大小为24,最大遗传进化代数为100,交叉概率为0.75,迭代计算结果经处理获得 Pareto 前沿如图 10 所示。
|
图 10 最大位移与质量Pareto图 Fig. 10 Maximum displacement and weight pareto diagram |
随机选择Pareto解集中的3点,最优点1位于Pareto前沿的最上端,最优点2位于Pareto前沿的最下端,最优点3位于Pareto前沿的中间,最优点1代表框架结构的质量最轻,有较好的经济性。最优点2表示框架的最大变形最小,结构稳定性最好。最优点3表明框架的稳定性和经济性适中。最终的设计还要根据实际情况来进行选择。表 3 列出了3种情况下具体的设计结果。
| 表 3 多目标优化计算结果 Table 3 Multi-objective optimization result |
本文分别对3个最优点进行有限元计算验证,计算表明:最优点1最大应力为187 MPa,最大变形为9.89 mm。最优点2最大应力为194 MPa,最大变形为9.16 mm。最优点3最大应力为189 Mpa,最大变形为9.36 mm。有限元验证值与近似模型计算值均有偏差,但都在精度允许范围内,可以接受。
| 表 4 多目标优化方案与初始方案比较表 Table 4 Multi-objective optimization program and initial design |
本文首先基于APDL建立框架结构参数化模型,并将Ansys与ISIGHT集成搭建了框架结构优化平台。对设计变量进行灵敏度分析,选出了对最大应力影响比较大的因素作为本文的优化设计变量。在此基础上建立近似模型,进行了轻量化单目标优化设计,结果表明框架重量较初始设计的1 949 kg 减轻了223 kg,约为11.44%。在轻量化基础上考虑结构稳定性,增加最大位移最小这一目标,进行了框架结构的多目标优化设计,优化结果表明既减小了框架的质量又增强了结构的稳定性,取得了预期优化效果。
| [1] |
陈明. 面向全过程的桥梁安全受控系统设计[J]. 计算机工程与设计, 2010, 31(14):3326-3330, 3335. CHEN Ming. Bridge safety control system design based on process-cycle[J]. Computer Engineering and Design, 2010, 31(14):3326-3330, 3335. |
| [2] |
张勇. 基于近似模型的汽车轻量化优化设计方法[D]. 长沙:湖南大学, 2008. ZHANG Yong. Optimization design method of vehicle lightweight based on approximate model[D]. Changsha:Hunan University, 2008. |
| [3] |
陈连. 求解任意梁的普遍化方法[J]. 机械工程学报, 2004, 40(12):71-74. CHEN Lian. General method for arbitrary beam analysis[J]. Chinese Journal of Mechanical Engineering, 2004, 40(12):71-74. |
| [4] |
吕亚楠. 地质体三维可视化应用研究[D]. 西安:长安大学, 2010. LV Ya-nan. Research on visualization of 3D geological body[D]. Xi'an:Chang'an University, 2010. |
| [5] |
李焱. 基于加权平均法和均匀设计的多目标进化算法[D]. 西安:西安电子科技大学, 2011. LI Yan. A multi-objective evolutionary algorithm based on weighted sum method and uniform design[D]. Xi'an:Xi'an University of Electronic Science and Technology, 2011. |
| [6] |
阮宏博. 基于遗传算法的工程多目标优化研究[D]. 大连:大连理工大学, 2007. RUAN Hong-bo. Study on multi-objective optimization of engineering project based on genetic algorithm[D]. Dalian:Dalian University of Technology, 2007. |
| [7] |
庞路. 优化算法在通信信号处理中的应用[D]. 济南:山东大学, 2011. PANG Lu. Applications of optimization algorithms in communication signal processing[D]. Jinan:Shandong University, 2011 |
| [8] |
王燕. 潜艇结构的优化设计方法研究[D]. 哈尔滨:哈尔滨工程大学, 2010. WANG Yan. Optimal design method research of submarine structure[D]. Harbin:Harbin Engineering University, 2010. |
 2016, Vol. 38
2016, Vol. 38
