船舶在其服役期间,会面临碰撞、冲击等问题,它直接关系到船舶的安全和使用寿命。船舶管路系统复杂又庞大,在进行整个系统的抗冲击性能的评估时无论是数值模拟技术或者是试验技术都很难对全部管路系统进行详尽分析和评估[1]。因此,根据管路系统冲击薄弱部位与船体或设备的连接特点,分别采用固定约束、简支约束和弹簧约束模拟不同的约束条件,给出该简化模型在冲击荷载作用下响应峰值的简化计算公式将对于工程应用意义重大。
我国在对船舶管路系统冲击进行研究时,多采用梁模型和有限元原理进行数值计算。在具体计算时,对于简单直管路应用模态分析法[2],同时解决了管路系统在冲击作用后的随机、周期性载荷或这2种载荷联合作用下的弹性支撑位置和数量优化。但由于管路系统动力学模型是偏微分方程,其解析解较难获得,因此在管路系统冲击研究中,数值计算和模拟被广泛地应用[3]。本文将结合这2种方法的优点进而综合获得管路系统抗冲击性能的工程简化计算公式。
1 模态分析的理论 1.1 频域理论对于多自由度比例阻尼系统的强迫振动,其运动方程为
| $ [M]\{\ddot{x}\}+[C]\{\dot{x}\}+[K]\{x\}=\{F\left( t \right)\}\text{。} $ | (1) |
采用模态叠加法,一般无阻尼其响应 $\{x\}$ 的正则变换表达式可写成:
| $ \{x\}=[ \phi]\{ q\}\text{。} $ | (2) |
式中:$[ \phi]$ 为固有振型矩阵,并将其作为坐标转换矩阵,该矩阵又称作固有振动模态振型矩阵或简称模态振型矩阵;$\{ q\}$ 为模态坐标向量。将方程(2)代入方程(1)再左乘 ${{[ \phi]}^{\rm{T}}}$(由于主振型的正交性)即可得到在无阻尼情况下的解耦的方程。
当有阻尼时,则根据 Reyleigh 假定,有一类阻尼可用下式表示
| $ [ C]=\alpha [ M]+\beta [ K]\text{,} $ | (3) |
| $ \{x\}=\sum\limits_{r=1}^{N}{\{{{\phi }_{r}}\}}{{q}_{r}}\text{。} $ | (4) |
对上式做拉氏变换后得:
| $ \{x\left( s \right)\}=\sum\limits_{r=1}^{N}{\{{{\phi }_{r}}\}{{q}_{r}}}(s)\text{,} $ | (5) |
将式(5)代入式(1)得
| $ [M](\sum\limits_{r = 1}^N {\{ {\phi _r}\} {s^2}{q_r}} (s)) + [C](\sum\limits_{r = 1}^N {\{ {\phi _r}\} s{q_r}} (s)) + \\ \quad\quad\quad\quad [K](\sum\limits_{r = 1}^N {\{ {\phi _r}\} {q_r}} (s)) = \{ F\left( s \right)\} \text{,} $ | (6) |
式(6)左乘以 ${{\{{{\phi }_{s}}\}}^{\rm{T}}}$,并考虑到正交关系:
$$ \begin{aligned} {\{ {\phi _s}\} ^{\rm T}}[ C]\{ {{ \phi} _r}\} = & \alpha {\{ {\phi _s}\} ^{\rm T}}[ M]\{ {\phi _r}\} + \beta {\{ {{ \phi} _s}\} ^T}[ K]\{ {{ \phi} _r}\} =\\ & \left\{ \begin{array}{l} 0,r \ne s\\ \alpha {m_s} + \beta {k_s} = {c_r},r = s\text{。} \end{array} \right. \end{aligned} $$ 式中 ${{c}_{r}}$ 为模态阻尼系数。上式初始条件为0的拉氏域方程(其中s为复变量)为:
| $ ({{s}^{2}}+2{{\xi }_{r}}{{\omega }_{r}}s+\omega _{r}^{2}){{q}_{r}}(s)={{\Lambda }_{r}}F(s)\quad ({r}=1,2,\ldots {N})\text{,} $ | (7) |
| $ {{q}_{r}}\left( s \right)=\frac{{{\Lambda }_{r}}F\left( s \right)}{{{s}^{2}}+2{{\xi }_{r}}{{\omega }_{r}}s+{{\omega }_{r}}^{2}}\quad ({r}=1,2,\ldots ,{N)}\text{。} $ | (8) |
将式(8)代回到式(4);在j点受一力的情况下在点i处的位移响应为:
| $ {{x}_{i}}(s)=\sum\limits_{r=1}^{N}{\frac{{{\Lambda }_{r}}{{F}_{j}}\left( s \right){{\phi }_{ir}}}{{{s}^{2}}+2{{\xi }_{r}}{{\omega }_{r}}s+{{\omega }_{r}}^{2}}}\text{。} $ | (9) |
式(9)即定义为i,j之间的频响函数。其物理意义是在j点作用单位力时,在i点所引起的响应。上述函数关系与激振力的频率有关,是在频域计算响应的重要公式,也可称为频域传递函数,简称频响函数。
对线性时不变系统,其极点在复平面左半平面,因此可将s换成jw,最终得在p点受一力的情况下在点i处的位移响应:
| $ {{x}_{i}}(\omega )=\sum\limits_{r=1}^{N}{\frac{{{\Lambda }_{r}}{{F}_{p}}\left( \omega \right){{\phi }_{ir}}}{-{{\omega }^{2}}+2{{\xi }_{r}}{{\omega }_{r}}j\omega +{{\omega }_{r}}^{2}}}\text{。} $ | (10) |
假设体系有n个自由度,在动载荷作用下,振动方程为:
| $ [ M]\{\ddot{x}\}+[ C]\{\dot{x}\}+[ K]\{x\}=\{{{F}_{p}}\left( t \right)\}\text{,} $ | (11) |
进行正则坐标变化
| $ \{x\}=[{ \phi}]\{q\}\text{。} $ | (12) |
当有阻尼时,则根据 Reyleigh 假定,有一类阻尼可用下式表示
$$ [ C]=\alpha [ M]+\beta [K]\text{。} $$ 其中α和β为比例常数。正则坐标q就是把实际位移x按主振型分解时的系数,即
$$ x={{\phi }_{1}}{{q}_{1}}+{{\phi }_{2}}{{q}_{2}}+\cdots +{{\phi }_{n}}{{q}_{n}}\text{。} $$将式(12)代入(11),再左乘 ${{[\phi]}^{\rm{T}}}$ 得:
| $ \begin{array}{l} {[{ \phi}]^{\rm T}}[ M][{ \phi}]\{ \ddot q\} + {[{ \phi}]^{\rm T}}[ C][{ \phi}]\{ \dot q\} + {[{ \phi}]^{\rm T}}[ K][{ \phi}]\{ q\} = \\ \quad\quad\quad {[{ \phi}]^{\rm T}}\{ {F_p}(t)\}\text{。} \end{array} $ | (13) |
则有 $diag[{{ m}_s}]\{ \ddot q\} + diag[{{ c}_s}]\{ \dot q\} + $$diag[{{ k}_s}]\{ q\} = \{ F(t)\} $,由于都是对角阵,即得包含n个独立方程:
$$ {{M}_{i}}{{\ddot{q}}_{i}}(t)+{{C}_{i}}{{\dot{q}}_{i}}(t)+{{K}_{i}}{{q}_{i}}(t)={{F}_{i}}(t)\quad (\text{i}=1,2,\ldots ,{n)}\text{,} $$上式两边同除以Mi得:
$$ {{\ddot{q}}_{i}}(t)+2{{\xi }_{i}}{{\omega }_{i}}{{\dot{q}}_{i}}(t)+\omega _{i}^{2}{{q}_{i}}(t)\!=\!\frac{1}{{{M}_{i}}}{{F}_{i}}(t)\text{,}\quad {i}=1,2,\ldots {n}\text{。} $$上一个方程用杜哈梅积分来写出,自由振动方程为:
$$ {{M}_{i}}{{\ddot{q}}_{i}}(t)+{{C}_{i}}{{\dot{q}}_{i}}(t)+{{K}_{i}}{{q}_{i}}(t)=0\text{。} $$在初位移和初速度给定的条件下有:
$$ {{q}_{i}}(t)={{e}^{-{{\xi }_{i}}{{\omega }_{i}}t}}({{q}_{i}}(0)\cos {\omega }{'}_{i}^{{}}t+\frac{{{\xi }_{i}}{{\omega }_{i}}{{q}_{i}}(0)+{{{\dot{q}}}_{i}}(0)}{{\omega }{'}_{i}^{{}}}\sin {{{\omega }{'}}_{i}}t)\text{。} $$式中:${{q}_{i}}(0)$,${{\dot{q}}_{i}}(0)$ 为体系的初始位移和初始速度;${{\xi }_{i}},{{\omega }_{i}}$ 为体系阻尼比和无阻尼的振动元频率;${{{\omega }{'}}_{i}}$ 为体系有阻尼的振动元频率。
假设体系受到大小为a的冲击加速度,在时间t内任一间隔 ${\rm d}\tau $ 体系获得冲量 $ma{\rm d}\tau $ 看成是时间 $\tau $ 处体系获得的动量增量。
$$ mv(\tau )=ma{\rm d}\tau \text{,} $$体系在时刻 $\tau $ 获得的初始速度为
| $ v(\tau )=a{\rm d}\tau \text{,} $ | (14) |
当 ${{q}_{i}}(0)$ = 0即静止状态,
| $ {{q}_{i}}(t)={{e}^{-{{\xi }_{i}}{{\omega }_{i}}(t)}}\frac{{{{\dot{q}}}_{i}}(0)}{{\omega }{'}_{i}^{{}}}\sin ({{{\omega }{'}}_{i}}t)\text{。} $ | (15) |
将式(14)代入式(15),得 $t>\tau $ 时刻,由初始速度 $v(\tau )$ 所引起的自由振动解
$$ {\rm d}{{q}_{i}}(t)={{e}^{-{{\xi }_{i}}{{\omega }_{i}}(t-\tau )}}\frac{a}{{\omega }{'}_{i}^{{}}}\sin {{{\omega }{'}}_{i}}(t-\tau ){\rm d}\tau \text{,} $$所以体系在t时刻的总响应可以看到是t之前所有冲量所引起的初速度的自由振动叠加,即
$$ {{q}_{i}}(t)=\int{d{{q}_{i}}(t)}=\int_{0}^{t}{{{e}^{-{{\xi }_{i}}{{\omega }_{i}}(t-\tau )}}\frac{a}{{\omega }{'}_{i}^{{}}}\sin {{{{\omega }{'}}}_{i}}(t-\tau ){\rm d}\tau } \text{,} $$得到最终解:
| $ \begin{array}{l} \displaystyle {q_i}(t) = {e^{ - {\xi _i}{\omega _i}t}}({q_i}(0)\cos \omega {'}_i^{}t + \frac{{{\xi _i}{\omega _i}{q_i}(0) + {{\dot q}_i}(0)}}{{\omega {'}_i^{}}}\sin {{\omega {'}}_i}t) + \\[10pt] \quad\quad\ \displaystyle \int_0^t {{e^{ - {\xi _i}{\omega _i}(t - \tau )}}\frac{a}{{\omega {'}_i^{}}}\sin {{\omega {'}}_i}(t - \tau ){\rm d}\tau } = \\ - 2a + {e^{ - {\xi _i}{\omega _i}t}}\left[{\cos \omega {'}_i^{}t({q_i}(0) + 2a) + } \right.\\ [8pt] \quad\quad \displaystyle \frac{{{\xi _i}{\omega _i}{q_i}(0) + {{\dot q}_i}(0)}}{{\omega {'}_i^{}}}\left. {\sin {{\omega {'}}_i}t} \right]\text{,} \end{array} $ | (16) |
化简得
| $ \begin{aligned} {q_i}(t) = - 2a + {e^{ - {\xi _i}{\omega _i}t}}\left[{\cos \omega {'}_i^{}t({q_i}(0) + } \right.\\ \left. {2a) + \displaystyle \frac{{{\xi _i}{\omega _i}{q_i}(0) + {{\dot q}_i}(0)}}{{\omega {'}_i^{}}}\sin {{\omega {'}}_i}t} \right]\text{。} \end{aligned} $ | (17) |
在具体问题上,qi(0)= 0,${\dot q_i}(0)$ = 0;对承受冲击载荷的结构来说,阻尼对控制结构的最大反应就显得不太重要。因为在冲击载荷下,很短的时间内结构就达到了最大反应。在这之前,阻尼力还来不及从结构吸收太多能量。所以一般讨论的是冲击载荷下体系的无阻尼反应。
无阻尼情况下,式(17)可改写为
$$ {q_i}(t) = - a + a\cos {\omega _i}t \text{。} $$对线性时不变系统,最终得在点i处无阻尼情况的位移响应:
| $ \{{{x}_{i}}\left( t \right)\}=\sum\limits_{r=1}^{N}{\{{{\phi }_{ir}}\}{{q}_{ir}}}(t)=\sum\limits_{r=1}^{N}{\{{{\phi }_{ir}}\}(}-a+a\cos {{\omega }_{ir}}t)\text{。} $ | (18) |
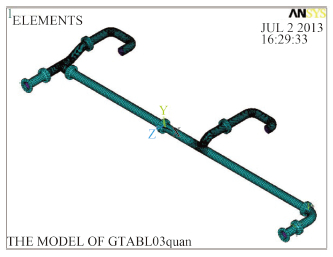
选用的简化管路系统采用 Ansys 软件中 APDL 参数化实体建模方法。简化模型采用管单元 pipe 16划分有限元网格,边界条件分别采用管道两端固定约束、简支约束和弹簧约束。选用的原管路系统的模型和简化具有分布集中质量的等效连续梁的模型,如图 1 和图 2 所示。
|
图 1 原典型管路系统模型 Fig. 1 The original typical model of pipeline system |

|
图 2 简化后的管路模型 Fig. 2 Simplified model of the pipeline |
在参数的提取、拟合过程中,对几个主要特征量的数值进行大量改变并进行有限元计算,如果考虑所有可能的组合,试验次数将会非常多[4],所以采用正交试验法来完成实验研究。经过经验和分析,长度L,管路外径D,壁厚t和约束形式是影响管路频率和振动特性的主要物理指标,因此针对本次试验设计了混合正交试验表 ${{L}_{30}}({{10}^{3}}\times 3)$。具体计算分析如图 3~图 6所示。
|
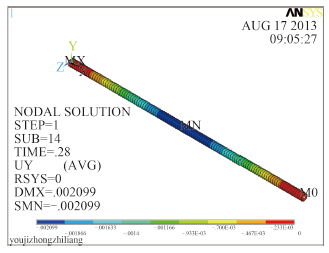
图 3 固支59号节点的最大位移云图 Fig. 3 The maximum displacement cloud of No. 59 node with fixed support |
|
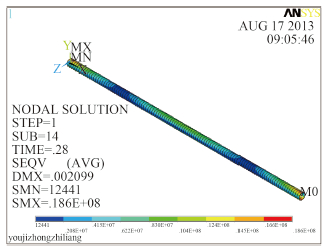
图 4 固支59号节点的最大应力云图 Fig. 4 The maximum stress cloud of No. 59 node with fixed support |
|
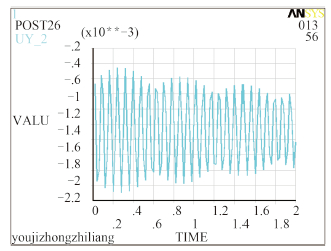
图 5 Ansys固支59号节点的位移时间曲线 Fig. 5 The displacement-time curve of No.59 node with fixed support in Ansys |
|
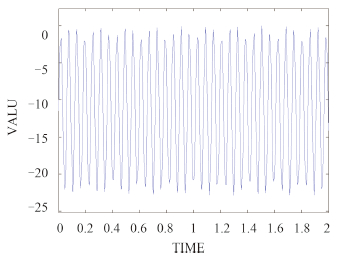
图 6 Matlab固支的位移时间曲线 Fig. 6 The displacement-time curve of No.59 node with fixed support in Matlab |
简化为有集中质量的管路模型,计算发现关键点(薄弱部位之一)的节点号为59,图 3~图 6 分别为固定支座情况下,关键节点的最大位移云图、最大应力云图、Ansys 的位移时间曲线和 Matlab 的位移时间曲线。
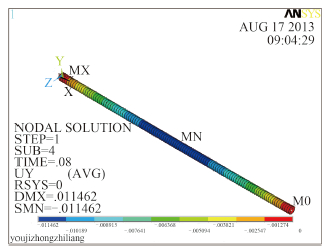
图 7 ~ 图 10 分别为简支情况下,关键节点的最大位移云图、最大应力云图、Ansys 的位移时间曲线和 Matlab 的位移时间曲线。
|
图 7 简支59号节点的最大位移云图 Fig. 7 The maximum displacement cloud of No. 59 node with simple support |
|
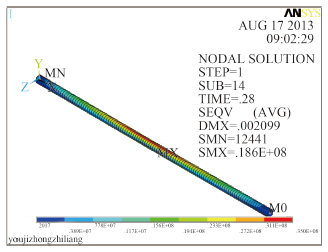
图 8 简支59号节点的最大应力云图 Fig. 8 The maximum stress cloud of No. 59 node with simple support |
|
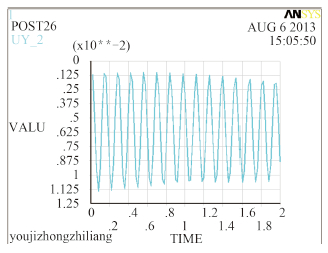
图 9 Ansys简支59号节点的位移时间曲线 Fig. 9 The displacement-time curve of No.59 node with simple support in Ansys |
|
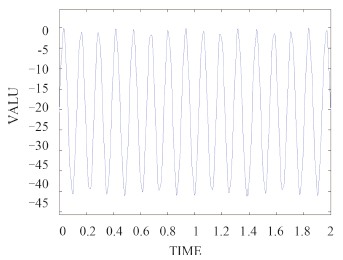
图 10 Matlab简支的位移时间曲线 Fig. 10 The displacement-time curve of No.59 node with simple support in Matlab |
图 11~图 14 分别为弹簧支座情况下,关键节点的最大位移云图及局部云图、最大应力云图及局部云图、Ansys 的位移时间曲线和 Matlab 的位移时间曲线。
|
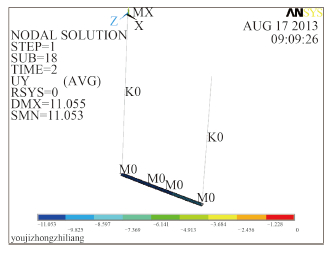
图 11 弹簧59号节点的最大应力云图 Fig. 11 The maximum displacement cloud of No. 59 node with spring support |
|
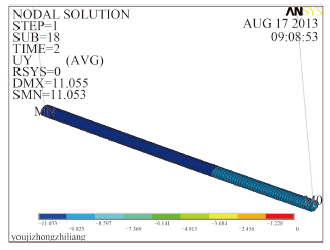
图 12 弹簧59号节点的最大应力云图(局部) Fig. 12 The maximum stress cloud of No. 59 node with spring support(local) |
|
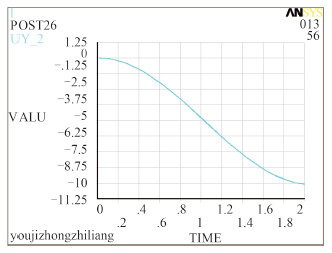
图 13 Ansys弹簧59号节点的位移时间曲线 Fig. 13 The displacement-time curve of No.59 node with spring support in Ansys |
|
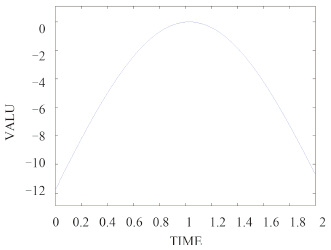
图 14 Matlab弹簧支撑的位移时间曲线 Fig. 14 The displacement-time curve of No.59 node with spring support in Matlab |
根据图 3~图 14 可知,Ansys 中关键位置的最大位移值分别为 -2.10 E-03 m,-1.15 E-02 m,10.078 2 m;发生的时间分别为0.28 s,0.08 s,2 s。Matlab 曲线中显示的理论值跟 Ansys 中显示的模拟值误差最大在20% 左右。
由于理论公式的最大值在t>0范围内找不到确定的唯一值,所以采取的方法是根据 Ansys 最大值发生的时间为参考,在 Matlab 中改变步长来寻找最接近的理论最大值。经过大量计算,从以上数据可看到:
1)弹性支撑的最大值相对固定支撑和简支大得多,一般是2~3个量级;
2)约束条件对对固有频率的影响最大;
3)理论值和 Ansys 的最大值误差在38% 左右。
2.3 理论公式简化之前学者的研究结果表明,管路系统模型参数中,材料密度对自由端的冲击响应最大值影响最大,管壁厚度影响其次,再其次是靠近自由端的弹簧刚度以及管的内径[8]。管路材料的弹性模量、远离自由端的弹簧刚度以及冲击作用时间间隔等其他参数对自由端最大位移的影响微乎其微。其中,材料密度、管壁厚度是两个和质量相关的量。灵敏度分析结果表明质量因素的影响最主要[5]。因此,在后续的参数拟合过程中,将对几个特征量数值进行大量改变并进行有限元计算,回归出典型管段位移、应力响应简化计算公式框架中各具体参数。
式(1)和式(2)分别给出了管路系统位移响应和应力响应的理论计算公式。在具体应用过程中需要确定各阶模态的频率、振型系数、模态阻尼比等参数[6]。而这些参数又与管路系统的尺寸相关联,是非常复杂的一个问题。对于管路系统的振动传递特性而言,其传递函数的前两个峰值非常重要,因此为了简化分析,取前3阶模态,即N= 3,则上述理论公式可简化为3阶模态的叠加。选用时域解的形式对理论结果与模拟结果进行对比分析,位移、应力解为:
| $ \begin{array}{l} {x_n}(t) = {\phi _{n1}}( - a + a\cos {\omega _1}t) + {\phi _{n2}}( - a + \\[8pt] \quad\quad\ \ \ a\cos {\omega _2}t) + {\phi _{n3}}( - a + a\cos {\omega _3}t)\text{;} \end{array} $ | (19) |
| $ \begin{array}{l} {\sigma _n}(t) = - {m_n}{\omega _1}^2{\phi _{n1}}a\cos {\omega _1}t - {m_n}{\omega _2}^2{\phi _{n2}}a\\ [8pt] \quad\quad\quad\,\,\ \cos {\omega _2}t - {m_n}{\omega _3}^2{\phi _{n3}}a\cos {\omega _3}t\text{。} \end{array} $ | (20) |
通过上述简化得到理论公式,下面通过大量的有限元计算来获得理论解和瞬态分析解,对比分析回归出工程简化理论计算公式。
2.4 响应面法回归公式中的参数响应曲面设计方法(Response Surface Methodology,RSM)是利用合理的试验设计方法并通过实验得到一定数据,采用多元二次回归方程来拟合因素与响应值之间的函数关系,通过对回归方程的分析来寻求最优工艺参数,解决多变量问题的一种统计方法。响应面法的基本思想是:通过一系列确定性实验,用多项式函数来近似隐式极限状态函数[7]。通过合理地选取试验点和迭代策略,来保证多项式函数能够在失效概率上收敛于真实的隐式极限状态函数的失效概率。
式(21)和式(22)是管路系统工程简化计算公式的时域解形式。位移、应力解分别为:
| $ \begin{array}{l} {x_n}(t) = {\phi _{n1}}( - a + a\cos {\omega _1}t) + {\phi _{n2}}\\[6pt] \quad\quad\quad ( - a + a\cos {\omega _2}t) + {\phi _{n3}}( - a + a\cos {\omega _3}t)\text{;} \end{array} $ | (21) |
| $ \begin{array}{l} {\sigma _n}(t) = - {m_n}{\omega _1}^2{\phi _{n1}}a\cos {\omega _1}t - {m_n}{\omega _2}^2{\phi _{n2}}a\\ [6pt]\quad\quad\ \ \ [10pt] \cos {\omega _2}t - {m_n}{\omega _3}^2{\phi _{n3}}a\cos {\omega _3}t \text{。} \end{array} $ | (22) |
其中回归公式的参数分别是 ${{\omega }_{1}}$,${{\omega }_{2}}$,${{\omega }_{3}}$,${{\phi }_{n1}}$,${{\phi }_{n2}}$,${{\phi }_{n3}}$,假设管路系统的响应幅值S是 ${{\omega }_{1}}$、${{\omega }_{2}}$、${{\omega }_{3}}$,${{\phi }_{n1}}$,${{\phi }_{n2}}$,${{\phi }_{n3}}$ 这几个参数的函数,这些参数(还有mn)又与管长L,管路半径D,壁厚t,约束及集中质量分布有关。假设S与L、D、t之间的关系如下:
| $ \begin{array}{l} S = {a_1} + {a_2}\times L + {\rm{ }}{a_3}\times D + {a_4}\times t + \\ [5pt]\quad \ \ {a_5}\times {L^2} + {a_6}\times {D^2} + {a_7}\times {t^2} + {a_8}\times L \times D + \\[5pt] \quad \ \ {a_9}\times D \times t + {a_{10}}\times L \times t \text{。} \end{array} $ | (23) |
表 1 参数回归结果显示,整体系数简支最大,而且部分符号是相反的,然后是固支,其次是弹性约束。对响应贡献最大的还是常数项和管长以及管子直径的系数;壁厚的系数跟约束条件有很大的关系,简支系数是其他的大概10倍;平方项简支大概是固支的2~4倍,是弹性约束的10倍左右;交叉项简支大概是固支的1~2倍,是弹性约束的3~10倍左右。可见,在相同响应值情况下,系数大的表明,约束条件对其响应影响更大,其余参数贡献很小;相反弹性约束时,L,D,t对响应的影响相对更大。而在L,D,t一定的情况下,简支的响应值最大,固支的最小。这只是纯理论和有限元研究,工程实际应用时还需要参考经验公式作一定的修正。
| 表 1 参数回归结果 Table 1 The results of the regression parameters |
管路系统的模型试验和数值模拟计算是分析和研究管路系统抗冲击及防护问题的基础和手段。本文在数值模拟和试验结论均已得的情况下,基于模态分析法的理论,推导给出了典型管路系统的简化模型在冲击荷载作用下的位移、应力响应工程简化计算公式。
根据管路系统冲击薄弱部位与船体或设备的连接特点,分别采用固定约束、简支约束和弹簧约束模拟不同的约束条件,基于模态分析法给出该简化模型在冲击荷载作用下响应峰值的简化计算公式框架。在此基础上结合参数化建模技术、有限元分析技术,采用抗冲击性能仿真方法通过大量数值计算,回归出典型管段位移响应幅值、应力响应幅值简化计算公式框架中各具体参数的计算方法,进而给出了管路系统抗冲击性能的工程简化计算公式。
| [1] | 汪玉, 华宏星. 舰船现代冲击理论及应用[M]. 北京:科学出版社, 2005:15-18. |
| [2] |
张智勇, 沈荣瀛, 王强. 充液管道系统的模态分析[J]. 固体力学学报, 2001, 22(2):143-149. ZHANG Zhi-yong, SHEN Rong-ying, WANG Qiang. The modal analysis of the liquid-filled pipe system[J]. Acta Mechnica Solida Sinica, 2001, 22(2):143-149. |
| [3] | LIANG C C, TAI Y S. Shock responses of a surface ship subjected to noncontact underwater explosions[J]. Ocean Engineering, 2006, 33(5/6):748-772. |
| [4] |
汪宏伟, 汪玉, 赵建华. 舰船管路系统冲击响应时域仿真及试验研究[J]. 武汉理工大学学报(交通科学与工程版), 2010, 34(4):746-748, 753. WANG Hong-wei, WANG Yu, ZHAO Jian-hua. Time tomain simulation and test of the shock response of shipboard piping system[J]. Journal of Wuhan UniversitY of Technology (TRansPortation Science & Engineering), 2010, 34(4):746-748, 753. |
| [5] |
李兆俊, 汪玉, 陈学德, 等. 管路系统冲击设计方法分析[J]. 振动与冲击, 2008, 27(9):171-174. LI Zhao-jun, WANG Yu, CHEN Xue-de, et al. Analysis for pipeline system shock design methods[J]. Journal of Vibration and Shock, 2008, 27(9):171-174. |
| [6] | PARKS E W. The permanent deformation of a cantilever struck Transversely at its tip[J]. Proceedings of the Royal Society a:Mathematical, Physical and Engineering Sciences, 1955, 228(1175):462-476. |
| [7] |
郭晋挺, 司马灿, 刘建湖, 等. 舰艇管路系统的抗冲击性能弹性评估方法[J]. 船舶力学, 2004, 8(4):108-115. GUO Jin-ting, SIMA Can, LIU Jian-hu, et al. A evaluation method for the anti-shock strength safety of shipboard pipelines in elastic domain[J]. Journal of Ship Mechanics, 2004, 8(4):108-115. |
| [8] |
汪宏伟, 汪玉. 管路系统结构及其参数对冲击响应的影响分析[J]. 船舶工程, 2009, 31(5):58-61. WANG Hong-wei, WANG Yu. Analysis of the influence of shock response of piping system to its structure and parameter[J]. Ship Engineering, 2009, 31(5):58-61. |
| [9] | DEGRASSI G, NIE J, HOFMAYER C. Seismic analysis of large-scale piping systems for the JNES-NUPEC ultimate strength piping test program[R]. NUREG/CR-6983, BNL-NUREG-81548-2008. U. S. NRC, 2008. |
 2016, Vol. 38
2016, Vol. 38
