随着船舶现代化的发展,船舶综合电力推进[1]已经逐渐成为船舶的主流推进方式。采用中压直流(Medium Voltage DC,MVDC)配电的船舶综合电力系统除了具备船舶综合电力系统本身的优点外,还具有能够提高系统的功率密度、节省空间、提高系统的效率等潜在的优点,因而成为了船舶综合电力系统未来的发展趋势[2, 3]。然而,与优点相对应的是系统复杂程度和控制难度的大大增加[4],需要有效的分析和研发工具从而充分发挥 MVDC 系统的优点。
建模与仿真在设计研发阶段能够成为船舶综合电力系统强有力的设计和分析工具。商用的数字仿真软件提供了丰富的模型库供用户使用。文献[5]利用Matlab初步实现了全电力推进船舶交流电力系统的数字仿真,具有进行稳态、动态仿真和谐波分析的功能;文献[6]利用PSCAD实现了船舶中压交流综合电力系统的数字仿真;文献[7]基于Simulink完成了低压直流电力系统的建模与仿真,利用自主构建的模型解决了系统结构复杂,仿真速度慢的缺点;文献[8]开展了初步的中压直流综合电力系统的数字仿真,但是其研究的工况较为单一,控制方式较为陈旧。
从以往国内外进行的船舶综合电力系统数字仿真研究来看,针对交流配电系统的仿真研究较多,也较为成熟;而针对直流配电系统的仿真研究则刚刚开始,针对MVDC系统的数字仿真则更加匮乏,使用的模型、控制方式以及仿真研究的工况都较具有一定的局限性。本文通过开展结构分析、数学模型等研究,实现了船舶MVDC综合电力系统的数字仿真。
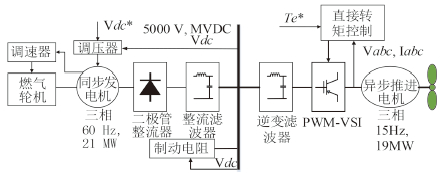
1 结构及特性分析本文研究的船舶MVDC综合电力系统的单线图如图 1所示[9],包含了系统各个典型的组成部分,由燃气轮机、转速控制器、同步发电机、励磁调压器、二极管整流器、整流滤波器、制动电阻、逆变滤波器、PWM电压源逆变器(PWM-VSI)、异步推进电机、船桨负载以及直接转矩控制系统组成。这样一种构成也使得系统的仿真体现出了一定的特性:
|
图 1 船舶中压直流综合电力系统组成结构示意图 Fig. 1 Configuration of the shipboard MVDC integrated propulsion system |
1)系统包含了动态特性差别较大的机械设备和电力电子变换器,系统的时间常数范围从纳秒级的电力电子开关时间常数到百秒级的船舶运动时间常数,因此,系统存在刚性的问题。
2)系统各部分之间联系紧密,为了使仿真更接近真实系统,必须考虑系统各设备之间的相互影响,也就是说,系统中的每个设备都要受到与其连接的设备的影响[10],因此,各模型之间的连接必须是双向的。
3)系统包含正常以及紧急情况下的多种运行工况,为了全面的对系统进行仿真,必须将系统的工况与船桨负载的特性结合起来。
针对船舶中压直流综合电力系统具有上述特性,本文选择了PLECS作为仿真工具[11, 12, 13],采用螺旋桨四象限负载同异步电机DTC结合的方法,实现了全系统正常和紧急情况下多种工况的仿真。
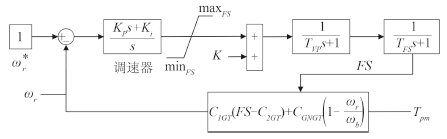
2 系统建模 2.1 发电系统的数学模型 2.1.1 原动机燃气轮机及调速器被作为原动机向同步发电机提供机械功率,在MVDC综合电力系统中,燃气轮机受到调速器的控制带动同步发电机始终以一个恒定的速度运行,原动机的动态响应和系统剩余部分的动态响应相互影响,本文采用了简化的单轴燃气轮机及其调速器的标幺值模型[14],其框图如图 2所示。
|
图 2 燃气轮机及调速器模型结构图 Fig. 2 Structure of the gas turbine with governor model |
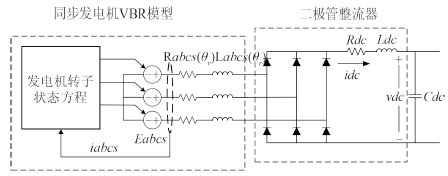
从图 1可知,在系统中,同步发电机和二极管整流器直接相连,如果采用传统的d-q轴模型,需要使用受控源实现d-q轴的动态模型,而受控源不能与二极管等非线性元器件直接相连,需要加入额外的缓冲电路。而VBR(Voltage-beind-reactance)模型的定子使用阻感支路建模,转子采用状态方程建模,采用VBR模型可以很好避免这一问题[15]。实现定子端直接同二极管整流器连接而不需要额外的缓冲电路,因此实现了在不损失模型精度的情况下仿真模型的简化,其示意图如图 3所示。
|
图 3 同步发电机VBR模型与二极管整流器结构图 Fig. 3 Configuration of the synchronous machine VBR model with diode rectifier |
二极管整流器可以采用仿真软件中提供的开关模型和平均值模型(AVM),AVM中[16]使用状态方程计算直流母线的电压
| $ p{\bar i_{dc}} = \frac{{\displaystyle\frac{{3\sqrt 3 }}{\pi }v_{qs}^g - \left( {{r_{dc}} + \displaystyle\frac{3}{\pi }{L_c}{\omega _b}} \right){i_{dc}} - {v_{dc}}}}{{{L_{dc}} + 2{L_c}}} \text{,}$ | (1) |
其中,$v_{qg}^g = \sqrt 2 E$,$v_{dg}^g = 0$。上标g代表二极管整流器 AVM 所在的参考坐标系,其d轴和o轴的电压均为0。E为发电机端电压的有效值。
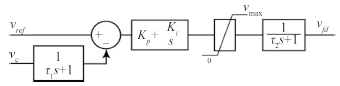
2.1.3 直流电压控制器传统的船舶交流综合电力系统中,系统的电压母线为三相交流,通过控制发电机的励磁来控制发电机输出的三相电压从而使得交流母线保持稳定,在船舶MVDC综合电力系统中通过控制励磁电压来直接控制直流母线电压的幅值,直流母线电压的控制结构如图 4所示。
|
图 4 直流电压控制器模型结构示意图 Fig. 4 DC voltage regulator-exciter |
由于同样为电力电子开关器件,PWM-VSI与二极管整理器相似,也可以通过开关模型和平均值模型两种方式进行建模,其中开关模型通常由仿真软件提供。为建立PWM-VSI的平均值模型,假设所有的开关都工作在连续导通的模式,则使用一个连续的正弦波对PWM进行平均[17]
| $ \left[{\begin{array}{*{20}{c}} {{v_a}}\\ {{v_b}}\\ {{v_c}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{m_a}}\\ {{m_b}}\\ {{m_c}} \end{array}} \right]{v_{dc}} \text{。}$ | (2) |
其中,m为调制比。相应的直流侧电流可以表示为
| $ {i_{dc}} = {m_a}{i_a} + {m_b}{i_b} + {m_c}{i_c} \text{。}$ | (3) |
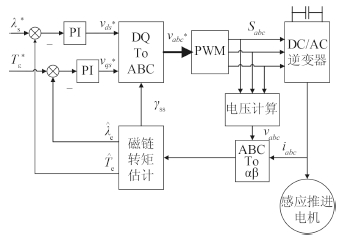
通过图 1可知,在推进系统,需要实现异步推进电机的转矩控制,通常使用的转矩控制方法主要有恒转差率控制[8]、直接转矩控制(DTC)[18]等。然而恒转差率控制不能实现电机的四象限驱动,直接转矩控制存在开关频率变化、起动和低速性能较差以及不能使用平均值的PWM-VSI进行建模等缺点,由于综合电力系统的异步推进电机和螺旋桨同轴相连,多工况的仿真需要实现四象限的运行,而且为了能够在DTC中使用PWM-VSI的平均值模型,本文采用了一种恒开关频率的异步推进电机直接转矩控制方法,其原理框图如图 5所示。
|
图 5 恒开关频率DTC控制框图 Fig. 5 Diagram of the constant switching DTC |
其中,异步推进电机的定子磁链和电磁转矩由2个PI控制器进行控制,其输出为定子磁链参考坐标系下的定子电压给定,PWM-VSI在使用仿真软件提供的开关模型时,其输入为PWM脉冲,在使用平均值模型时,其输入为正弦电压信号。
2.2.3 船桨负载船舶综合电力系统的运行工况与螺旋桨负载的特性具有紧密的联系,为了进行多种不同工况的运行,进行四象限螺旋桨的建模。
旋桨旋转时产生的阻转矩和推力可分别表示为[19]:
| $ {T_{prop}} = {K_Q}\rho {n^2}{D^5}\text{,} $ | (4) |
| $ {F_{prop}} = {K_T}\rho {n^2}{D^4}\text{,} $ | (5) |
其中,KQ为无量纲的转矩系数,ρ为海水密度,kg/m3;n为螺旋桨的转速,r/s;D为螺旋桨的直径,m。在考虑四象限负载特性的情况下,其可以表示为进速系数J的函数,有
| $ {K_Q} = \frac{\pi }{8}C_Q^*({J^2} + {(0.7\pi )^2}), $ | (6) |
| $ {K_T} = \frac{\pi }{8}C_T^*({J^2} + {(0.7\pi )^2})\text{。} $ | (7) |
其中,$C_Q^*$和$C_T^*$为无量纲的四象限转矩系数和推力系数,J为进速比,可表示为:
| $ J \equiv \frac{{{V_a}}}{{nD}}, $ | (8) |
其中,Va为船舶的进速,m/s。
$C_Q^*$和$C_T^*$均为螺旋桨对于水的前进角的单值函数,可表示为:
| $ C_Q^* = f(\beta ), $ | (9) |
| $ C_T^* = g\left( \beta \right)\text{。} $ | (10) |
其中,β为前进角,为相对于水的速度相量同叶片速度相量之间的夹角,有
| $\begin{array}{l} \beta = {\tan ^{ - 1}}(\displaystyle\frac{{{V_a}}}{{{V_b}}}) = {\tan ^{ - 1}}(\displaystyle\frac{{{V_a}}}{{2\pi nr}}) = \\ \;\;\;\;\;\;{\tan ^{ - 1}}(\displaystyle\frac{{{V_a}}}{{\pi n \cdot 70\% D}}) = {\tan ^{ - 1}}(\displaystyle\frac{J}{{0.7\pi }})\text{。} \end{array}$ | (11) |
前进角β的变化描述了船舶综合电力系统螺旋桨工作的4个象限,从而定义了船舶综合电力系统运行的不同工况。如表 1所示。
| 表 1 螺旋桨工况与前进角对应的关系 Tab.1 Propeller operating conditions correspond to β |
当螺旋桨正转,且船舶前向航行时,系统工作在第一象限,在突然倒车的开始时,螺旋桨迅速反转,而船舶本身的惯性时间常数比较大,会出现一个缓慢减速的过程,此时,螺旋桨反转,而船舶仍向前航行,则系统工作在第2象限,异步推进电机将向MVDC母线回馈能量。当螺旋桨反转,船舶的航速降为0时,反转的螺旋桨将推进船舶向后航向,此时异步推进电机又将进入电动状态,系统将工作在第三象限。当螺旋桨反转并推进船舶向后航行时,突然正转螺旋桨,此时,由于船舶的航速不能突变,系统将工作在第四象限,其情况与第2象限类似。船舶综合电力系统在第一象限和第3象限都能稳定运行,而第2象限和第四象限则是2个过渡的工况。
船舶在静水中的前向加速运动可以通过牛顿第二定律得到[20]:
| $\frac{{{\rm{d}}{V_a}}}{{{\rm{d}}t}} = \frac{{\left( {{F_{prop1}} + {F_{prop2}}} \right)(1 - t) - {F_{drag}}}}{{m \cdot {m_a}}}\text{。}$ | (12) |
其中,Va为船舶的前向运行速度,m/s ;t为推力减额系数(无量纲);Fdrag为船体向后的航行阻力,N;m为船舶的质量,kg;ma为受到船舶航行影响的船舶的附加质量系数(无量纲)。由于受到船体和周围水流的影响,船舶的航速和船舶的前进速度往往并不相等,其关系可以表示为:
| ${V_a} = V(1 - w)\text{。}$ | (13) |
其中,w为泰勒伴流系数(无量纲)。
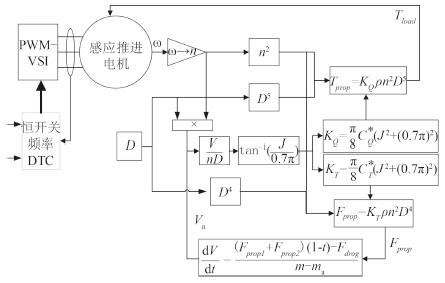
根据船桨负载模型,本文给出螺旋桨四象限负载和异步推进电机恒开关频率 DTC 系统之间的结合关系如图 6所示。
|
图 6 恒开关频率DTC控制框图 Fig. 6 Diagram of the constant switching DTC |
在机理模型的基础上,在PLECS中构建仿真算例对系统进行数字仿真,仿真所使用的参数如下[21]:
燃气轮机及其调速器参数:Kp= 8,Kt= 3,TVP= 0.5,TFS= 0.2;
21 MW三相同步发电机参数:Rr= 1.27 mΩ,Rfd= 401 mΩ,Rkd= 4.74 mΩ,Rkq= 5.26 mΩ,Lls= 391 μH,Lmq= 2.51 mH,Lmd= 2.79 mH,Llfd= 227 μH,Llkd= 69.8 μH,Llkq= 157 μH,P= 2,fb= 60 Hz;
直流电压控制器参数:τ1= 0.001,Kp= 0.1,Ki= 0.05,Vmax= 150,τ2= 0.02;
19MW 异步推进电机参数:Rs= 27 mΩ,Rr= 8 mΩ,f= 15 Hz,Lls= 1.5 mH,Llr= 1.7 mH,Lm= 31.7 mH;
螺旋桨及船体参数:D= 5.5 m,ρ= 1 025 kg/m3,w= 0.2,td= 0.04,m = 1.325×107kg,ma= 1.08。
本算例进行船舶中压直流综合电力系统多工况的仿真,仿真的工况既包括系统的起动、加速等正常工况,也包括了系统突然倒车的极端工况,在突然倒车工况中,船舶需要紧急制动并使得船舶的航向从全速前进到向相反的方向航行。由于螺旋桨的反转使得船舶快速停车并反向航行是船舶综合电力系统承受的最为严重的工况之一。
对于船舶MVDC综合电力系统来说,在突然倒车的情况下,采用双向的推进电机驱动系统能够将倒车产生的能量回馈到直流母线处,由于采用直流电网的形式,这部分能量将在直流母线处进行处理,采用在直流母线处加入制动电阻的方式将回馈的能量以热能的形式消耗掉。为不使热量耗散过大,使用控制器对直流侧制动电阻回路的开关进行控制,将MVDC总线的直流电压控制在6 kV以内,当电压超过6 kV时,控制器开始工作,从而使得母线的电压不超过6 kV。在制动电路模型建立完毕之后进行船舶MVDC综合电力系统突然倒车工况的仿真,仿真结果如图 7~图 10所示。
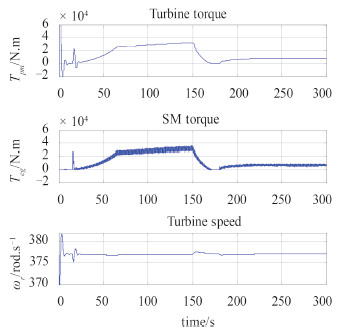
|
图 7 燃气轮机转矩、发电机电磁转矩和转速结果 Fig. 7 Simulation results of the turbine torque, SM EM torque and turbine speed |
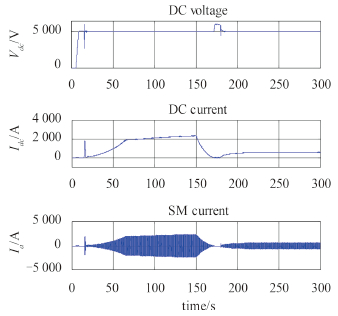
|
图 8 直流母线电压、电流和发电机相电流结果 Fig. 8 Simulation results of the MVDC voltage,current and SM phase current |
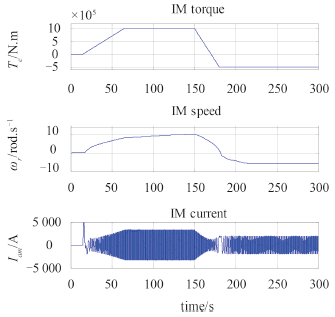
|
图 9 推进电机电磁转矩、转速和相电流结果 Fig. 9 Simulation results of the IM EM torque, rotational speed and phase current |
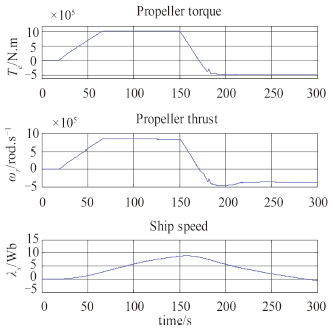
|
图 10 螺旋桨阻转矩、推力和船舶航速结果 Fig. 10 Simulation results of the propeller load torque, thrust and ship speed |
图 7~图 10分别给出了船舶MVDC综合电力系统在突然倒车工况下的燃气轮机输出机械转矩、同步发电机电磁转矩、燃气轮机转速、直流母线电压、直流母线电流、同步发电机相电压、异步推进电机电磁转矩、转速、相电流、螺旋桨的阻转矩、推力、船舶航行的速度、燃气轮机输出的机械功率、直流母线功率、异步推进电机输出机械功率的仿真结果曲线。
从图 7~图 10的仿真结果曲线可看出,仿真开始时,首先进行励磁系统的动态过程,建立5 kV直流母线电压,在15 s时起动推进电机,给定推进电机的电磁转矩1 MN.m,50 s后推进电机的电磁转矩达到给定值,此时,异步推进电机的转速开始逐渐趋于稳定,系统的其他状态也逐渐趋于稳定,船舶将以大约18 kn 稳定航行;150 s时,突然将给定电磁转矩在30 s内从1 MN.m 降至-0.5 MN.m,随着电磁转矩给定的降低,系统的各个变量开始从原有的水平降低,其中异步推进电机的转速缓慢降低,在异步推进电机的转矩将为0而其转速为正转这段时间内,船舶仍旧保持前向行驶,大约从170 s~ 180 s,推进系统进入能量回馈状态,在能量回馈状态下,直流母线电压升高,受到制动回路的控制作用而保持在6 kV,燃气轮机输出的转矩、发电机的电磁转矩、直流母线电流为0,在能量回馈阶段,燃气轮机的输出功率和直流母线的功率均为0,而异步推进电机输出的机械功率为负值,表明其进入了发电状态;在180 s之后,异步推进电机的转速反转,推进系统重新进入电动状态,系统的各个变量开始增加,并最终稳定,异步推进电机的转速稳定在-6 rad/s,在螺旋桨反转的作用下,船舶缓慢减速,在290 s时航速降为0,开始向后航行。
4 结语本文建立了MVDC综合电力系统的仿真模型,能够满足系统仿真的需要。给出了四象限的螺旋桨和船舶运动负载与异步推进电机DTC系统结合的过程,首次实现了船舶MVDC综合电力系统在正常和紧急等多个不同工况下的动态仿真,仿真结果表明了所进行的仿真的正确性。本文的工作为今后中压直流配电船舶综合电力系统的设计和研发奠定了基础。
| [1] |
马伟明. 舰船动力发展的方向——综合电力系统[J]. 海军工程大学学报, 2002, 14(6):1-5, 9. MA Wei-ming. Integrated power systems——trend of ship power development[J]. Journal of Naval University of Engineering, 2002, 14(6):1-5, 9. |
| [2] | DOERRY N, MCCOY K. Next generation integrated power system:NGIPS technology development roadmap[R]. Washington DC:Naval Sea Systems Command, 2007. |
| [3] |
刘胜, 张玉廷, 余辰光. 船舶电力推进系统电机组三维模糊控制[J]. 中国电机工程学报, 2012, 32(3):117-123. LIU Sheng, ZHANG Yu-ting, YU Chen-guang. Three-dimensional fuzzy control for ship electric propulsion turbine[J]. Proceedings of the CSEE, 2012, 32(3):117-123. |
| [4] | LIU S, CHENG Y Z. Modeling of a twelve-phase synchronous machine using Matlab/Simpowersystems[C]//Proceedings of International Conference on Electronics, Communications and Control. Ningbo:IEEE, 2011:2131-2134. |
| [5] |
王淼, 戴剑锋, 周双喜, 等. 全电力推进船舶电力系统的数字仿真[J]. 电工技术学报, 2006, 21(4):62-67. WANG Miao, DAI Jian-feng, ZHOU Shuang-xi, et al. Digital simulation of ship power system with electric propulsion[J]. Transactions of China Electrotechnical Society, 2006, 21(4):62-67. |
| [6] | CHOU H M, ITUZARO F A, BUTLER-PURRY K L. A PC-based test bed for NG IPS for ships in PSCADTM[C]//Proceedings of IEEE Electric Ship Technologies Symposium (ESTS). Alexandria, VA:IEEE, 2011:135-142. |
| [7] | ZAHEDI B, NORUM L E. Modeling and simulation of all-electric ships with low voltage DC hybrid power systems[J]. IEEE Transactions on Power Electronics, 2013, 28(10):4525-4537. |
| [8] | MARDEN MM, PREMPRANEERACH P, KIRTLEY J L, et al. An end-to-end simulator for the all-electric ship MVDC integrated power system[C]//Proceedings of the 2010 Conference on Grand Challenges in Modeling & Simulation. Vista, CA:Society for Modeling & Simulation International, 2010:136-143. |
| [9] | BASH M, CHAN R R, CRIDER J, et al. A medium voltage DC testbed for ship power system research[C]//Proceedings of IEEE Electric Ship Technologies Symposium. Baltimore, MD:IEEE, 2009:560-567. |
| [10] | APSLEY J M, GONZALEZ-VILLASENOR A, BARNES M, et al. Propulsion drive models for full electric marine propulsion systems[J]. IEEE Transactions on Industry Applications, 2009, 45(2):676-684. |
| [11] | SIMULINK. Dynamic system simulation software users manual[EB/OL]. Math Works. http://www.mathworks.com. |
| [12] | ALIMELING J H, HAMMER W P. PLECS-piece-wise linear electrical circuit simulation for Simulink[C]//Proceedings of the IEEE 1999 International Conference on Power Electronics and Drive Systems. Hong Kong:IEEE, 1999, 1:355-360. |
| [13] |
王成山, 李鹏, 黄碧斌, 等. 一种计及多重开关的电力电子时域仿真插值算法[J]. 电工技术学报, 2010, 25(6):83-88. WANG Cheng-shan, LI Peng, HUANG Bi-bin, et al. An interpolation algorithm for time-domain simulation of power electronics circuit considering multiple switching events[J]. Transactions of China Electrotechnical Society, 2010, 25(6):83-88.. |
| [14] | ROWEN W I. Simplified mathematical representations of heavy-duty gas turbines[J]. Journal of Engineering for Power, 1983, 105(4):865-869. |
| [15] | MAYER J S, WASYNCZUK O. An efficient method of simulating stiffly connected power systems with stator and network transients included[J]. IEEE Transactions on Power Systems, 1991, 6(3):922-929. |
| [16] | KRAUSE P C, WASYNCZUK O, SUDHOFF S D, et al. Analysis of electric machinery and drive systems[M]. 3rd ed. New York:Wiley, 2013. |
| [17] | RIM C T, CHOI N S, CHO G C, et al. A complete DC and AC analysis of three-phase controlled-current PWM rectifier using circuit D-Q transformation[J]. IEEE Transactions on Power Electronics, 1994, 9(4):390-396. |
| [18] | TAKAHASHI I, NOGUCHI T. A new quick-response and high-efficiency control strategy of an induction motor[J]. IEEE Transactions on Industry Applications, 1986, IA-22(5):820-827. |
| [19] | TUPPER E C, RAWSON K J. Basic ship theory[M]. Boston:Butterworth-Heinemann, 2001. |
| [20] | HOLSONBACK C R. Dynamic thermal-mechanical-electrical modeling of the integrated power system of a national all-electric naval surface ship[D]. Texas:University of Texas at Austin, 2007. |
| [21] | MILOŠEVIĆ M, PREMPRANEERACH P, KIRTLEY J L, et al. An end-to-end simulator for the all-electric ship MVDC integrated power system[C]//Proceedings of the 2010 Conference on Grand Challenges in Modeling & Simulation. Vista, CA:Society for Modeling & Simulation International, 2010:136-143. |
 2016, Vol. 38
2016, Vol. 38
