在船舶设计领域中，二维翼型的应用非常广泛，因而其设计也显得相当重要，如舵剖面的设计和对翼型升阻比要求比较高的螺旋桨叶剖面的设计^[1]。而且随着设计要求的复杂化，如何得到合理的翼型使其能同时满足多目标、多学科的要求就显得尤为重要。

对于螺旋桨来说，单独追求高效率已成为过去时，兼顾空泡性能才是当今时代的主题。因而，如何在保证高效的同时又能兼顾其空泡性能成为研究热点，相应地，适用于这种情况的翼剖面还很少，这就必须对翼剖面进行优化设计，于是就产生了翼剖面的多目标优化设计问题。

早期螺旋桨剖面多采用 NACA 66 mod +a= 0.8，但其越来越不能满足所需兼顾的高效和空泡性能，因而就必须对螺旋桨的翼剖面进行优化设计。而近年来，随着计算流体动力学（CFD）及计算机的飞速发展，集成 CFD 技术和新兴优化算法（如遗传算法、粒子群优化算法）从而形成的 SBD（Simulation Based Design）设计方法已成为一大关注热点^[2]。利用该方法进行优化设计，为解决复杂非线性问题提供了良好的思路，为构型优化设计打开了新的局面^[3]，而其应用于二维翼剖面优化设计方面也取得了相应的进展。常欣^[1]、许平等^[4]利用该思想优化翼型时，对翼型的描述都采用了解析函数线性叠加法，所选定的目标函数则均只是高升阻比，但目标函数的求解则分别采用了面元法和响应面模型。总之，这些工作多采用多项式拟合或解析函数线性叠加来表达翼型剖面^{[1, 4, 5, 6]}，设计变量较多，增加了设计问题的复杂度；而在计算水动性能时多采用势流法或借助于构建的响应面模型^{[1, 4, 7]}，因而对于流动细节的模拟存在一定的差异，所选定的优化目标则比较单一，其工程应用受限。

本文引入数学上的 NURBS 曲线来表达翼型几何，利用其控制点成功实现变形与重构，然后基于 Isight 优化平台，结合 CFD 技术等构建了二维翼剖面的自动优化设计流程；并选择与常用桨叶剖面翼型相近的且有实验结果的 NACA 66₁-212 为设计对象，兼顾效率和空泡性能，以升阻比和最小压力系数为目标进行优化设计。

为构建翼型自动优化设计流程，首先，要采用适当的方法对翼型几何进行准确的描述，同时又能够灵活实现翼型的几何变形与重构；其次，采用合理的数值计算方法得到翼型的水动特性，从而指导优化设计的方向；最后，利用 Isight 优化平台及其自带的优化算法来集成整个优化设计过程。

翼剖面优化设计过程中，选取合适的翼剖面几何表达方法尤为重要。因为一方面要考虑采用何种方法才能准确表达翼型几何外形，另一方面，基于这种表达方法要能够便捷地实现二维翼型的几何变形与重构。

传统的翼型几何表达方法多采用解析函数线性叠加^{[8, 9, 10]}或多项式拟合^{[5, 6]}。如若采用解析函数线性叠加，则翼型的形状由基准翼型、型函数及其系数来决定。总之，这些方法所需的设计变量就会比较多，且翼型构型设计空间存在一定的局限性。

而非均匀有理 B 样条（NURBS）在复杂目标建模方面有许多优点^[5]，因而被广泛地应用于工业产品自由曲线的表达。本文尝试采用 3 次 NURBS 曲线来对翼型进行几何表达，同时利用 NURBS 曲线控制点位置的变化来达到翼型几何重构的目的。

一个p次 B 样条曲线的定义为：

节点矢量U（共m+ 1 个节点）的形式为：

除非特别声明，一般假定a= 0，b= 1。由 {P_i} 构成的多边形称为控制多边形。NURBS 曲线的形状与控制点 {P_i} 的位置密切相关，根据控制点 {P_i} 的位置变化，就能生成变化后的翼型，从而实现翼型几何的重构。

NURBS 曲线为自由曲线的表达提供了一个公共的数学表示，能够利用较少控制点的变化来灵活实现翼型几何的重构，而这些控制点的位置又可以直接作为优化设计问题中的设计变量。实际操作时，这些过程可以运用自编的 Matlab 程序来实现。

本文应用 Fluent 商用软件，采用 RANS 方法来求解翼型的水动力特性：对流采用二阶迎风差分格式；扩散项采用中心差分格式。湍流模型对二维翼型粘性绕流问题计算结果的影响很小^[11]，因而采用二方程的湍流模型 SSTk-ω。其中翼型长度为 1 m，攻角设为 2°，来流条件设为 9 m/s，雷诺数为 10⁶。

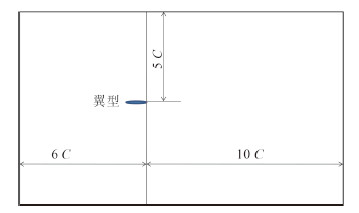
同时，采用 Gambit 软件进行网格划分工作，选定的计算域如图 1 所示，对翼型周围的区域要进行局部加密，距离翼型表面的第 1 层网格的距离则根据计算的雷诺数来取定。通过网格收敛性等分析^[12]，最后折衷考虑计算效率和计算精度，计算采用的网格数都为 59 400。

图 1 计算域划分 Fig. 1 Computational domain

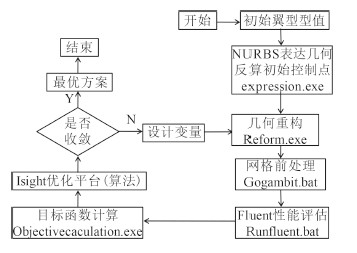
基于 Isight 平台，构建的优化设计自动流程如图 2 所示。对于不同的初始翼型，首先要获得用 NURBS 曲线来表达几何时的初始控制点，将这些控制点的位置作为设计变量。随后根据不同的设计变量值，采用几何重构方法，生成新的翼型几何型值，导入 Gambit 软件自动完成网格划分，然后利用 CFD 进行求解计算，进而获得目标函数值，利用 Isight 平台提供的适用于多峰性等复杂问题的全局优化算法——多目标粒子群优化算法（Multi-objective Particle Swarm Optimization）对构型设计空间进行探索，得到新的设计变量值，重复以上过程，最终获得最优解或最优解集。

图 2 优化设计自动流程 Fig. 2 The flow chart of design optimization

对于二维翼型的优化设计，大多数的研究只是单纯追求高升阻比^[13]。而对于螺旋桨来说，最需要关心的2个设计目标是效率和空泡性能。螺旋桨在水中工作时，若某处的压力降至临界值（该温度时水的汽化压力）以下导致爆发式的汽化，形成的气泡现象称为空泡^[14]。因而，只要最小压力系数越高，就越不容易产生空泡^[15]。或者说，要延迟空化初生，就要控制叶背压力分布，使其不出现较高的叶背负压峰。

相应于本文二维翼型剖面的设计，选取升阻比和最小压力系数作为设计目标，设计得到的升阻比和最小压力系数值越大越好。

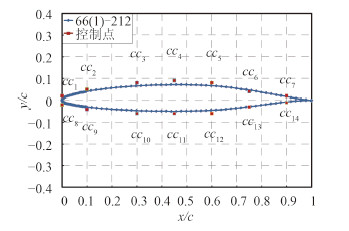
螺旋桨最常用的翼型是 NACA 66 mod +a= 0.8，因而选择与该剖面翼型相近且有实验结果的 NACA 66₁-212 作为研究对象（见图 3）。

图 3 NACA 661-212 翼型及上下表面控制点 Fig. 3 The airfoil geometry of NACA 661-212 and control points

应用 NURBS 曲线表达方法，最终针对 NACA 66₁-212 选定的设计变量（即控制点）如图 3 所示，这样就可以利用控制点的变化来实现翼型的自动变形与重构。

而对于设计问题的约束条件而言，一方面，要给定设计变量一定的变化范围，然而变化范围幅度又不能太大，这样可以较好地控制翼型的变形，相对于初始翼型，得到的结果不至于面目全非，因而最终选定的设计变量范围如表 1，最终的构型设计空间较小。另一方面还要考虑，翼型剖面的水动力约束，通常情况下对翼型优化希望看到的是，升力增大阻力减小的情况，因此相应地要加上约束条件：优化后的升力系数值不低于初始翼型的升力系数值。

表 1(Tab.1)

表 1 设计变量取值范围 Tab.1 The range of design variables 设计变量 cc 1 cc 2 cc 3 cc 4 cc 5 cc 6 cc 7 上限(1/ c) 0.012 0.042 0.072 0.082 0.072 0.032 0.012 下限(1/ c) 0.028 0.058 0.088 0.098 0.088 0.048 0.028 设计变量 cc8 cc9 cc10 cc11 cc12 cc13 cc14 上限(1/ c) –0.014 –0.034 –0.054 –0.054 –0.054 –0.024 –0.004 下限(1/ c) –0.026 –0.046 –0.066 –0.066 –0.066 –0.036 –0.016

表 1 设计变量取值范围 Tab.1 The range of design variables

在运用多目标粒子群优化算法进行优化之前，先用 DOE（Design of Experiments）试验设计方法对设计空间进行简单的探索，并分析了设计变量对相应目标函数的贡献度，会发现前缘附近的参数对升阻比是正影响，而对最小压力系数却是负影响。由此可见，设定的两目标函数之间存在一定的矛盾性。

采用多目标粒子群优化算法进行优化设计，其中选定的初始种群数为 40，最大迭代次数为 25，惯性权重为 0.9，全局增量为 0.9，粒子增量为 0.9，最大速度为 0.1。

待整个优化设计过程完成后，从所得的 Pareto 解集中选取3个具有代表性的优化方案进行具体分析。这3个方案分别是升阻比收益最大、最小压力系数收益最大以及升阻比和最小压力系数收益均比较大的方案。这3个方案的具体收益见表 2。

表 2(Tab.2)

表 2 优化方案收益对比 Tab.2 Comparison of the objective functions of the optimized airfoils 升阻比 K 收益/% C p min 收益/% OPT1 26.11 –8.31 OPT2 20.55 21.36 OPT3 7.53 22.79

表 2 优化方案收益对比 Tab.2 Comparison of the objective functions of the optimized airfoils

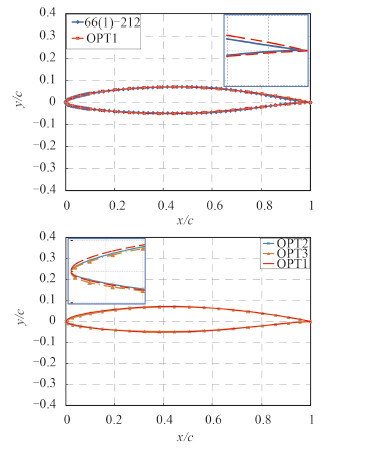
根据 3 个方案的设计参数，可以生成相应翼型。图 4 是设计方案 OPT1,OPT2 和 OPT3 对应的翼型对比图。分析对比可得，前后缘附近控制点比较关键，也就是说翼型前后缘附近的形状对翼型升阻比和最小压力系数的影响均比较大。相应于初始翼型，后缘附近的形状变化趋势比较一致，优化翼型在后缘处的厚度均有所增加，其过渡更加自然。由此可见，初始翼型在后缘处的形状存在一定的改动空间。而前缘附近拱度对升阻比的影响较大，拱度越大，升阻比越高，这符合拱度对翼型升阻比的影响规律。OPT1 方案的前缘附近拱度最大，因而升阻比收益最大。而前缘附近拱度大的，其导边处叶背负压峰就会大大提高，因而其最小压力系数值是负收益（负值），对于最小压力系数来说，前缘处形状变化平缓的更有利。

图 4 优化解对应的翼型与初始翼型的对比（小框中的为局部放大图） Fig. 4 Comparison of the geometry of the original airfoil and the optimized airfoils

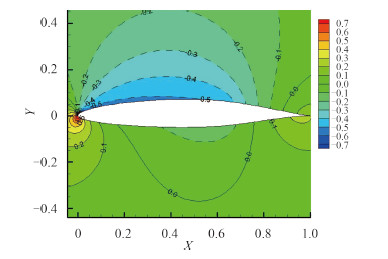
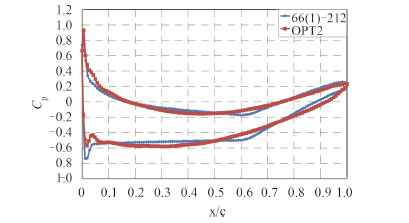
图 5 和图 6 分别为初始翼型和 OPT2 翼型表面的压力分布云图。图 7 为翼型表面压力系数分布对比图。观察发现，优化后的翼型最小压力系数值明显提高，猜测对起始空泡性能会有所改善；优化后的翼型其翼段中部的压力系数相比初始翼型偏低，而正是上下表面压力差（即围成的面积大小）提供了升力，因而优化后的升力系数明显优于初始翼型。

图 5 初始翼型表面压力分布云图 Fig. 5 The pressure distribution contour of the original airfoil

图 6 OPT2 翼型表面压力分布云图 Fig. 6 The pressure distribution contour of the OPT2 airfoil

图 7 OPT1 与初始翼型表面压力系数分布 Fig. 7 Comparison of the pressure coefficient distribution of the original airfoil and the OPT2 airfoil

进一步考虑优化所得的翼型在非设计工况（攻角）时的水动特性。选取优化方案 OPT2，利用 CFD 技术对其在非设计攻角（0°，4°）下的水动性能进行评估，并与初始翼型的水动性能进行比较（表 3）。从表 3 中可以看出，优化翼型 OPT2 在攻角 0°时的综合水动性能优于初始翼型。而在攻角为 4°时的最小压力系数值虽优于初始翼型，但其升阻比却不够理想。因而，在后续作进一步研究时，可以考虑将多攻角下的水动性能作为优化设计目标。

表 3(Tab.3)

表 3 OPT2 与初始翼型在非设计攻角下的水动性能 Tab.3 The hydrodynamic performance of the original airfoil and OPT2 at non-design attacks 攻角(/°) 升阻比 K 最小压力系数 c p min 初始翼型 OPT2 初始翼型 OPT2 0 19.04 21.83 –0.44 –0.45 2（设计攻角） 33.91 40.88 –0.74 –0.58 4 40.26 34.52 –1.60 –1.17

表 3 OPT2 与初始翼型在非设计攻角下的水动性能 Tab.3 The hydrodynamic performance of the original airfoil and OPT2 at non-design attacks

本文尝试运用 NURBS 曲线对翼型几何进行表达，实现了翼型几何的重构与变形。并通过集成 CFD 技术、优化算法等构建了二维翼型优化设计的自动流程。同时以 NACA 66₁-212 为研究对象，进行考虑升阻比和最小压力系数的多目标优化设计，结果表明了该方法的可行性，为后续进一步开展三维螺旋桨优化设计打下了基础。