2. 中国科学院上海技术物理研究所, 上海 200080;
3. 中国科学院红外探测与成像技术重点实验室, 上海 200080;
4. 上海市现场物证重点实验室, 上海 200080
2. Shanghai Institute of Technical Physics of the Chinese Academy of Sciences, Shanghai, 200080, China;
3. Key Laboratory of Infrared System Detection and Imaging Technology, Chinese Academy of Sciences, Shanghai, 200080, China;
4. Shanghai Key Laboratory of Crime Scene Evidence, Shanghai, 200080, China
稳定平台通常用于隔离舰船、车辆等运动载体的扰动,使其装载的观测仪器相对于大地坐标系保持静止。楔形稳定平台是一种新型稳定平台。它最先由荷兰信号公司设计[1],现已应用于舰载“天狼星”远程红外搜索与跟踪系统[2]。与陀螺仪式稳定平台不同,楔形稳定平台主要由若干自由转动的楔块组成。楔块的转动能改变顶部平面的倾角,若倾角时时与载体摇摆的方向相反,就能抵消扰动。
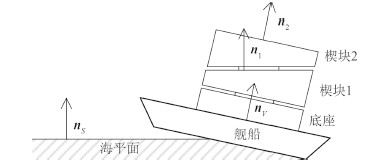
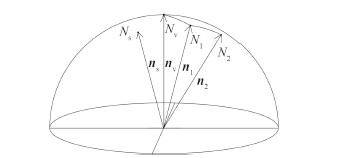
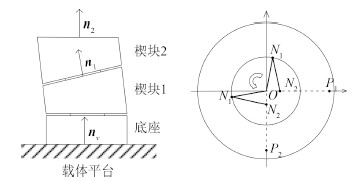
1 等效机械臂模型推导楔块的转动与顶部平面倾角的变化关系并不直观。为了使分析更为形象,在此先引入等效机械臂的概念。图 2中,ns,nv,n1 和n2 分别为海平面、舰船和2个楔块上平面的单位法向量。假定nv 静止,则舰船摇动等效于ns 相对于nv 摆动。再假设楔块夹角均为β,则n1 与nv 和n2 与n1 的夹角也是β。那么当楔块 1 旋转时,n1 以固定夹角β 围绕nv 旋转。同理当楔块2旋转时,n2 以固定夹角β 围绕n1 旋转。将上述单位向量平移使它们的起点重合,从而终点位于同一单位球面(见图 3)。于是三维空间内楔块的旋转可以等效为二维球面空间内 $ \mathop {{N_v}{N_1}}\limits^{\frown} $圆心做相同角度的旋转。

|
图 1 “天狼星”系统的楔形稳定平台[3] Fig. 1 The wedge-platform of Sirius IRST |
|
图 2 海平面、舰船和楔形稳定平台的单位法向量示意图 Fig. 2 Schematic diagram of unit normal vectors of sea level, vessel and wedge-platform |
|
图 3 海平面、舰船和楔形稳定平台的单位法向量球面图 Fig. 3 Sphere map of unit normal vectors of sea level, vessel and wedge-platform |
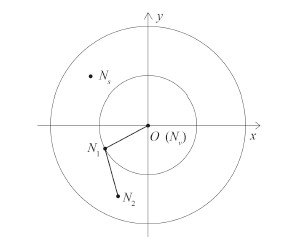
因为船摇的角度和楔块的楔角都比较小,所以点Ns,N1,N2 均仅在以Nv 为中心的小范围内运动。在不影响定性分析准确性的前提下,不妨用从北极方向看去的平面投影(简称“平面图”)代替球面图,同时将球面上的弧近似为平面上的线段。平面图中y 轴沿舰船纵轴方向指向船首,x 轴沿横轴方向指向右舷。Ns 在Nv 周围一定区域内做随机运动,线段 ON1 围绕 O(Nv)旋转,N1N2 围绕N1 旋转,转角大小等于楔块转动的角度。根据2个线段的运动形态,可以将 ON1 和N1N2 等效为一个二维自由度机械臂的上臂和前臂,O 和N1 等效为机械臂肩关节和肘关节,N2 等效为机械手。用等效机械臂模型来描述楔形稳定平台的工作原理,就是控制机械臂 ON1N2 让机械手N2 实时跟踪目标点Ns 的运动。
|
图 4 平面图和等效机械臂 Fig. 4 Plane graph and equivalent manipulator |
在设计楔形稳定平台的机械结构时,必须考虑楔角和层级结构。楔角主要影响平定平台的补偿范围,而层级结构则对平台的补偿效果有决定性影响。
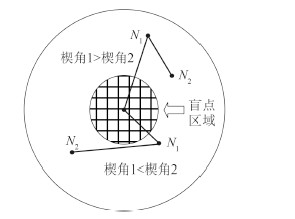
2.1 楔块的楔角平面图中等效机械臂的臂长与楔角大小成正比,同时臂长决定了活动范围。较大的楔角虽然能增加活动范围,但也会使整体重心不稳。对于双层结构楔形稳定平台而言如果2个楔角不相等(即臂长不相等),机械手将无法触及肩关节及其附近的盲点区域。因此双层结构的2个楔角必须相等。多层结构虽然没有这个问题,但在设计时也应当考虑到楔角变化对控制效果的影响,合理设计每层楔块的楔角大小。
2.2 双层结构双层结构是指由一个水平底座和2个可旋转的楔块组成的楔形稳定平台的设计结构。平面图中双层结构等效为上臂与前臂等长的机械臂,且肩关节与原点重合。虽然这种结构最为简单,但是它有一个明显缺陷——当跟踪轨迹过肩关节(原点)时,上臂(楔块 1)会发生“转角阶跃”(转角变化不连续)。为说明这个情况,不妨假设目标点的运行轨迹为P1 经过O 到P2 的一段折线(见图 6)。机械臂可以在P1O 上方运行或者下方运行,两者没有本质区别。假定在上方运行,当目标点沿着P1O 经过原点时,机械臂与y 轴重合。然而当目标点转向沿着OP2 运行时,上臂必须突然转动 90°到与y 轴垂直的位置才能使机械手继续沿着OP2 运动。但实际上伺服系统的阶跃响应需要较长时间,因此“转角阶跃”无法精确实现的。这就会导致双层结构楔形稳定平台的跟踪精度大大下降。
|
图 5 楔角不相等时双层结构楔形稳定平台的盲点区域 Fig. 5 Blind zone of 2-layer structure when wedge angles are not equal |
|
图 6 双层结构和“转角阶跃”示意图 Fig. 6 Schematic diagram of 2-layer structure and rotation angle step |
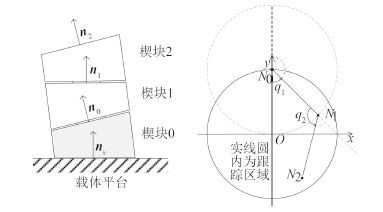
之所以发生“转角阶跃”是因为机械手要经过与原点重合的肩关节。若将肩关节与原点分开,就可以避免这个问题。为此可以将底座改成相同楔角的楔块(称为楔块 0)。从平面图上看楔块 0 的作用是将肩关节从原点移到了跟踪区域外的N0。可以证明在肩关节和肘关节连续转动的情况下,机械手能够跟踪区域内的任意轨迹。并且针对每一个区域内的点,上臂和前臂的转角q1,q2(0°≤q1≤180°,0°≤q2≤180°)有且只有唯一解。
2.4 多层结构如果有 3 层或 3 层以上可旋转的楔块,则称之为多层结构。平面图中多层结构等效为 3 节或 3 节以上机械臂。虽然多层结构提供了更高的控制灵活性,但是鉴于双层结构已经能够达到二维活动空间的自由度要求,增设的楔块不仅提高了成本,而且多层结构中楔块转角的解不唯一,徒增控制复杂度。
3. 楔形块转角的控制函数通过第2节对不同的楔形稳定平台的结构分析比较不难发现,改进型双层结构平衡了可用性和经济性,符合大多数情况下对稳台的需求。接下来介绍改进型双层结构楔形稳定平台的控制函数及求解方法。
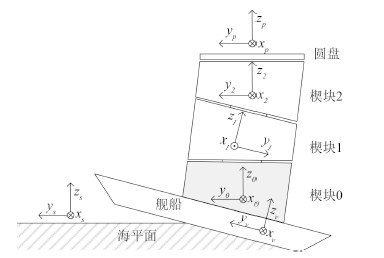
3.1 平台系统中坐标系的定义因为楔形稳定平台主要用于隔离舰船偏航、横滚和纵摇 3 种旋转扰动的影响,所以忽略各坐标系原点的相对位置而仅考虑各坐标系间旋转关系。首先对初始状态下各坐标系的相对位置做设定。
自下而上依次为大地坐标系:zs 指向天空与海平面垂直,ys 指向正北,xs 指向正东;舰船载体坐标系:zv 轴指向舰船载体正上方与装载平面垂直,yv 轴指向舰首,xv 轴指向右舷,初始状态下舰船坐标系与大地坐标系重合;楔块 0 坐标系:z0 垂直于楔块 0 上平面,y0 轴指向楔角方向,x0 轴与z0 和y0 成右手螺旋关系,初始状态下x0 指向右舷;楔块 1 坐标系:z1 垂直于楔块 1 上平面,y1 轴指向楔角方向,x1 轴与z1 和y1 成右手螺旋关系,初始状态下x1 指向左舷;楔块2坐标系:z2 垂直于楔块2上平面,y2 轴指向楔角方向,x2 轴与z2 和y2 成右手螺旋关系,初始状态下x2 指向右舷;圆盘坐标系:zp 垂直于圆盘,yp,xp与zp 成右手螺旋关系,初始状态下圆盘坐标系与楔块2坐标系重合。
3.2 旋转矩阵和坐标系转换旋转的正方向和转角根据初始状态坐标系以右手螺旋法则确定。按照我国惯用的惯性元件检测顺序,从大地坐标系向舰船坐标系的转换应按照偏航-横滚-纵摇的顺序进行[4]。用H、R、P 分别表示偏航角、横滚角和纵摇角,那么
偏航旋转矩阵:
| $ {{{M}}_H} = \left[{\begin{array}{*{20}{c}} {\cos (H)}\\ { - \sin (H)}\\ 0 \end{array}\begin{array}{*{20}{c}} {\sin (H)}\\ {{\rm{cos}}(H)}\\ 0 \end{array}\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right] \text{;} $ | (1) |
横滚旋转矩阵:
| $ {{{M}}_R} = \left[{\begin{array}{*{20}{c}} {\cos (R)}\\ 0\\ {{\rm{sin}}(R)} \end{array}\begin{array}{*{20}{c}} 0\\ 1\\ 0 \end{array}\begin{array}{*{20}{c}} { - {\rm{sin}} (R)}\\ 0\\ {\cos (R)} \end{array}} \right]\text{;} $ | (2) |
纵摇旋转矩阵:
| $ {{{M}}_P} = \left[{\begin{array}{*{20}{c}} 1\\ 0\\ 0 \end{array}\begin{array}{*{20}{c}} 0\\ {\cos (P)}\\ { - {\rm{sin}}(P)} \end{array}\begin{array}{*{20}{c}} 0\\ {{\rm{sin}}(P)}\\ {\cos (P)} \end{array}} \right]\text{;} $ | (3) |
船摇扰动等效矩阵:
| $ {{{M}}_{dist}} = {{{M}}_P}{{{M}}_R}{{{M}}_H}\text{。} $ | (4) |
楔块对坐标系旋转变化的影响包括转角旋转和楔角旋转2个部分。分别用β 表示楔角,q1、q2 和q3 表示楔块 1、楔块2和圆盘的转角,那么
楔角旋转矩阵:
| $ {{{M}}_\beta } = \left[{\begin{array}{*{20}{c}} 1\\ 0\\ 0 \end{array}\begin{array}{*{20}{c}} 0\\ {\cos (\beta )}\\ {{\rm{sin}}(\beta )} \end{array}\begin{array}{*{20}{c}} 0\\ { - {\rm{sin}}(\beta )}\\ {\cos (\beta )} \end{array}} \right]\text{;} $ | (5) |
楔块 1 转角旋转矩阵:
| $ {{{M}}_{r1}} = \left[{\begin{array}{*{20}{c}} { - \cos (q_1)}\\ {\sin (q_1)}\\ 0 \end{array}\begin{array}{*{20}{c}} { - \sin (q_1)}\\ { - \cos (q_1)}\\ 0 \end{array}\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right]\text{;} $ | (6) |
楔块2转角旋转矩阵:
| $ {{{M}}_{r2}} = \left[{\begin{array}{*{20}{c}} { - \cos (q_2)}\\ {\sin (q_2)}\\ 0 \end{array}\begin{array}{*{20}{c}} { - \sin (q_2)}\\ { - \cos (q_2)}\\ 0 \end{array}\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right]\text{;} $ | (7) |
顶圆盘转角旋转矩阵:
| $ {{{M}}_{r3}} = \left[{\begin{array}{*{20}{c}} {\cos (q_3)}\\ { - \sin (q_3)}\\ 0 \end{array}\begin{array}{*{20}{c}} {\sin (q_3)}\\ {\cos (q_3)}\\ 0 \end{array}\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right]\text{;} $ | (8) |
补偿等效旋转矩阵:
| $ {{{M}}_{comp}} = {{{M}}_{r3}}{{{M}}_\beta }{{{M}}_{r2}}{{{M}}_\beta }{{{M}}_{r1}}{{{M}}_\beta } \text{;} $ | (9) |
于是从大地坐标系到圆盘坐标系的完整变换过程可以用这些旋转矩阵的乘积来表示:
| $ {{{M}}_{total}} = {{{M}}_{comp}}{{{M}}_{dist}}\text{。} $ | (10) |
楔形稳定平台可以准确补偿偏航、横滚和纵摇 3 个方向的任何扰动,也就是说对于大地坐标系的任意被观测向量a 在经过扰动和补偿之后,在圆盘坐标系上应当保持不变[5]。用向量和旋转矩阵则表示为:
| $ a = {{{M}}_{total}}a\text{,} $ | (11) |
即
| $ a = {{{M}}_{r3}}{{{M}}_\beta }{{{M}}_{r2}}{{{M}}_\beta }{{ M}_{r1}}{{ M}_\beta }{{ M}_P}{{ M}_R}{{ M}_H}a\text{。} $ | (12) |
| $ {({{{M}}_{r3}}{{{M}}_\beta }{{{M}}_{r2}}{{{M}}_\beta })^{ - 1}}a{'} = {{{M}}_{r1}}{{{M}}_\beta }{{ M}_P}{{ M}_R}{{ M}_H}a{'}\text{。} $ | (13) |
由上式可以算得:
| $ \begin{array}{l} \cos ({q_2}) = \left[\cos (\beta )\cos(P) \right.\cos (R) - {\cos ^2}(b) + \\[4pt] \quad\quad\quad\quad \left. {{\rm{sin}}(\beta )\cos(R){\rm{sin}}(P)} \right] \div {{\rm{sin}} ^2}(\beta ) \end{array}\text{,} $ | (14) |
| $ \begin{array}{l} \cos ({q_1}) = \left[{\sin (\beta )\sin ({q_2})} \right.\sin (R) - \\[6pt] \quad\quad\quad\quad \sin (\beta )\cos^2(\beta )\cos (R)\sin (P) + \\[6pt] \quad\quad\quad\quad \sin (\beta ){\cos ^2}(\beta )\cos({q_2})\cos (R)\sin(P) + \\[6pt] \quad\quad\quad\quad \cos (\beta )\cos (P)\sin{^2}(\beta )\cos (R) - \\[6pt] \quad\quad\quad\quad \left. {\cos (\beta )\cos (P)\cos ({q_2}){{\sin }^2}(\beta )\cos(R)} \right]{\rm{ \div }}\\[6pt] \quad\quad\quad\quad \left[{{{\sin }^2}(R)} \right. + {\cos ^2}(\beta )\cos{^2}(R)\sin{^2}(P) + \\[6pt] \quad\quad\quad\quad \cos{^2}(P){\rm \sin}{^2}(\beta )\cos{^2}(R)-\\[6pt] \quad\quad\quad\quad \left. {2\cos (\beta )\cos (P)\sin (\beta ){{\cos }^2}(R)\sin(P)} \right]\text{。} \end{array} $ | (15) |
因为q1 与q2 的取值范围都是 0°~180°(见图 7),所以应当通过 cos(q1)和 cos(q2)计算q1 和q2。
| $ {q_1} = {\rm{arccos}}\left( {\cos \left( {{q_1}} \right)} \right)\text{,} $ | (16) |
| $ {q_2} = {\rm{arccos}}\left( {\cos \left( {{q_2}} \right)} \right)\text{。} $ | (17) |
|
图 7 改进双层结构的示意图和平面图 Fig. 7 Schematic diagram and plane graph of advanced 2-layer structure |

|
图 8 多层结构的示意图和平面图 Fig. 8 Schematic diagram and plane graph of multi-layer structure |
|
图 9 各坐标系相对关系示意图 Fig. 9 Schematic diagram of relative coordinate systems |
式中q3 为圆盘的转角,用于补偿水平方向上偏航扰动和楔块 1 和楔块2转动时附加的影响,因此可以取$ a{''} = {(1,0,0)^{\rm T}} $。由于q3 的取值范围是 0°~360°,所以要综合考虑 cos(q3)和 sin(q3)才能计算q3。调整式(12)并代入a"
| $ {{M}}_{r3}^{ - 1}a{''} = {{{M}}_\beta }{{{M}}_{r2}}{{{M}}_\beta }{{{M}}_{r1}}{{{M}}_\beta }{{{M}}_P}{{{M}}_R}{{{M}}_H}{\rm{a''}}\text{。} $ | (18) |
计算可得:
| $ \begin{aligned} \cos ({q_3}) = & {\rm{cos}}(H){\rm{sin}}(R){\rm{sin}}(P)[{\rm{sin}}({q_2}){\rm{si}}{{\rm{n}}^2}(\beta ) + \cos \left( \beta \right)\left( {\cos \left( {{q_2}} \right)\sin \left( {{q_1}} \right) + } \right.\left. {\left. {\cos \left( \beta \right)\cos\left( {{q_1}} \right)\sin \left( {{q_2}} \right)} \right)} \right] \\ & \cos \left( P \right)\left[{\sin \left( \beta \right)\left( {\cos \left( {{q_2}} \right)\sin \left( {{q_1}} \right) + } \right.} \right.\left. {\cos \left( \beta \right)\cos \left( {{q_1}} \right)\sin \left( {{q_2}} \right)} \right] - \left. {\left. {\cos \left( \beta \right)\sin \left( \beta \right)\sin \left( {{q_2}} \right)} \right]} \right\} + \\ & \cos \left( {\rm{R}} \right)(\cos \left( {{q_1}} \right)\cos \left( {{q_2}} \right) - \cos \left( \beta \right)\sin \left( {{q_1}} \right)\sin \left( {{q_2}} \right))\} - {\rm{sin}}\left( H \right)\{ \sin \left( P \right)\left[{\sin \left( \beta \right)\left( {\cos \left( {{q_2}} \right)} \right.\sin \left( {{q_1}} \right) + } \right.\\ & \cos \left( \beta \right)\cos \left( {{q_1}} \right)\sin \left( {{q_2}} \right) - {\rm{cos}}\left( \beta \right){\rm{sin}}\left( \beta \right)\left. {{\rm{sin}}\left( {{q_2}} \right)} \right] + {\rm{cos}}\left( P \right)\left[{\sin \left( {{q_2}} \right)} \right.\sin{^2}\left( \beta \right) + {\cos}\left( \beta \right)\left( {\cos \left( {{q_2}} \right)} \right.\sin \left( {{q_1}} \right) + \\ & \cos \left( \beta \right) \cos \left( {{q_1}} \right)\left. {\left. {\left. {\sin \left( {{q_2}} \right)} \right)} \right]} \right\}\text{,} \end{aligned} $ | (19) |
| $ \begin{aligned} \sin \left( {{q_3}} \right) = & \sin \left( H \right)\{ \cos \left( P \right)\left\{ {\sin \left( \beta \right)} \right.\left( {\cos \left( \beta \right)} \right.\sin \left( \beta \right) - \cos \left( \beta \right)\cos \left( {{q_2}} \right)\left. {\sin \left( \beta \right)} \right) - \cos \left( \beta \right)\left[{\cos \left( {{q_1}} \right)} \right.\left( {\cos \left( {{q_2}} \right)} \right.\cos{^2}\left( b \right) + \\ & \sin{^2}\left( \beta \right)) - \cos \left( \beta \right)\sin \left( {{q_1}} \right)\left. {\left. {\sin \left( {{q_2}} \right)} \right]} \right\} - \sin \left( P \right)\left\{ {\cos \left( \beta \right)} \right.\left( {\cos \left( \beta \right)} \right.\sin \left( \beta \right) - \cos \left( \beta \right)\cos \left( {{q_2}} \right)\left. {\sin \left( \beta \right)} \right) + \\ & \sin \left( \beta \right)\left[{\left[{\cos \left( {{q_1}} \right)} \right.\left( {\cos \left( {{q_2}} \right)} \right.} \right.\cos{^2}\left( \beta \right) + \left. {\sin{^2}\left( \beta \right)} \right) - \cos \left( \beta \right)\sin \left( {{q_1}} \right)\left. {\left. {\left. {\sin \left( {{q_2}} \right)} \right]} \right\}} \right\} - \cos \left( H \right)\left\{ {\cos \left( R \right) \cdot } \right.\\ & \left[{\sin \left( {{q_1}} \right)} \right.\left( {\cos \left( {{q_2}} \right)} \right.\cos{^2}\left( \beta \right) + \left. {\sin{^2}\left( \beta \right)} \right) + \cos \left( \beta \right)\cos \left( {{q_1}} \right)\sin \left( {{q_2}} \right)] + \sin\left( R \right)\left\{ {\cos \left( P \right)} \right.\left\{ {\cos \left( \beta \right)} \right. \cdot \\ & \left( {\cos \left( \beta \right)\sin \left( \beta \right) - \cos \left( \beta \right)\cos \left( {{q_2}} \right)\left. {\sin \left( \beta \right)} \right)} \right. + \sin \left( \beta \right)\left[{\cos \left( {{q_1}} \right)\left( {\cos \left( {{q_2}} \right)\cos{^2}\left( \beta \right) + \left. {\sin{^2}\left( \beta \right)} \right) - } \right.} \right.\\ & \cos \left( \beta \right)\sin \left( {{q_1}} \right)\left. {\left. {\left. {\sin \left( {{q_2}} \right)} \right)} \right]} \right\} + \sin \left( P \right)\left\{ {\sin \left( \beta \right)(\cos \left( \beta \right)\sin \left( \beta \right) - } \right.\cos \left( \beta \right)\cos \left( {{q_2}} \right)\left. {\sin \left( \beta \right)} \right) - \\ & \cos \left( \beta \right)\left[{\left[{\cos \left( {{q_1}} \right)\left( {\cos({q_2}} \right)} \right.} \right.{\cos ^2}\left( \beta \right) + {\rm{ }}{\sin ^2}\left( \beta \right) - \cos \left( \beta \right)\sin \left( {{q_1}} \right)\left. {\left. {\left. \!\!\!\!{\left. {\left. {\sin ({q_2})} \right)} \right]} \right\}} \right\}} \right\}\text{。} \end{aligned} $ | (20) |
| $ {q_3} = \left\{ {\begin{array}{*{20}{c}} {\arccos \left( {\cos \left( {{q_3}} \right)} \right)\;\;\;\;\;\;\;\;\text{,}{\rm{sin}}\left( {{q_3}} \right)\geqslant 0}\text{;}\\[3pt] {2\pi - \arccos \left( {\cos \left( {{q_3}} \right)} \right)\text{,}\sin \left( {{q_3}} \right) < 0}\text{。} \end{array}} \right. $ | (21) |
楔块的转角变化比平台的倾角高一个数量级,因此它的控制精度高。又因为楔块基本是在水平面转动,所以伺服电机的负载转矩小,也因此质量轻、能耗低。加之它的结构简单,相对于陀螺仪式稳定平台它的制造成本也更低。总之,楔形稳定平台为稳定平台的设计提供了一种有益的新思路。
| [1] | MAAS A J. Wedge platform stabilization[J]. Revue Technique-Thomson-CSF, 1994, 26(3):553-569. |
| [2] | 孙成禄. 甩不掉的"尾巴"——舰载"天狼星"远程红外搜索与跟踪系统[J]. 现代兵器, 2004(6):28-29. |
| [3] | 郭隆华. 加拿大海军验收首套天狼星红外搜索与跟踪系统[EB/OL]. (2008-5-20). http://news.xinhuanet.com/mil/2008-05/20/content_8213388.html. |
| [4] |
张志远, 罗国富. 舰船姿态坐标变换及稳定补偿分析[J]. 舰船科学技术, 2009, 31(4):34-40. ZHANG Zhi-yuan, LUO Guo-fu. Coordinate transformation of warship pose and analysis of stabilization compensation[J]. Ship Science and Technology, 2009, 31(4):34-40. |
| [5] | 张坤石. 潜艇光电装备技术[M]. 哈尔滨:哈尔滨工程大学出版社, 2007:429-437. |
 2016, Vol. 38
2016, Vol. 38
