2. 浙江水利水电学院 机械与汽车工程学院, 浙江 杭州 310018
2. College of Machinery and Automobile Engineering, Zhejiang University of Water Resources and Electric Power, Hangzhou 310018 China
随着陆地和浅海油气资源的不断衰竭,寻找和开发新的油气资源引起了整个世界的关注。近年来,全球新增油气探明储量大部分来自于深水,也发现了多个大型油气田,己形成墨西哥湾、西非和巴西海域3个深水油气勘探开发中心[1, 2]。
深海油气资源的开发离不开相应设备的支持[3],特别是平台的系泊系统。国外学者对深海平台的系泊系统的静力分析做了大量研究。Smith 等[4]采用拉格朗日迭代,用悬链线方程对深水海域中由 2 段索链组成的复合系泊线进行了静力分析。T M Smith[5] 比较了由全链、全索及链索结合系泊线组成的锚泊系统,结果是链索结合的系统和全链系统相比,在提供相同的回复力情况下重量较轻。而国内在这方面的研究也已取得一定成果。周洋[6]根据单一成分悬链线方程的推导方法综合考虑多种材料的特性进行限定水深范围的多成份系泊线悬链线方程的推导。王冬姣[7]利用悬链线方程,对由3段单位长度质量和尺度各不相同的索链与水中浮子或沉子组合而成的复合系泊线进行了静力分析。
本文根据悬链线方程[8, 9]对深水系泊系统进行静力计算分析,与张火明[10, 11]工作相结合,运用迭代法和二分法相结合的方法计算系泊缆的水平力,得到系泊缆的关键数据,据此绘制系泊悬链线。以工作水深 1 000 m 的两成分系泊验证文中系泊悬链线方程和系泊缆的水平力计算方法的正确性,并对一工作水深为 2 000 m 的绷紧索系泊系统三成分系泊进行计算。
1 无弹性多成分悬链线方程工作水深的不断增加,单一成分的悬链线己不能满足工程的需要,故现在的深水系泊一般采用索链结合的方式。为方便计算,假设如下:
1)该系泊缆索在一个平面内,上端为平台的导缆孔,下端为与海床的接触点;
2)将系泊缆索视为非线性弹簧。
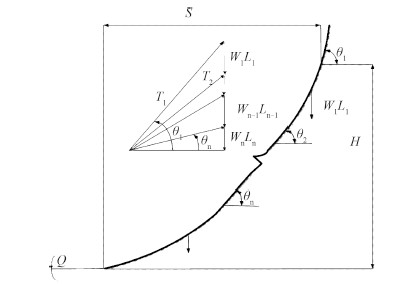
系泊系统的计算模型可简化为由多条均布的非线性弹簧支持的刚体在垂直平面内的运动体系。在每个时刻系泊系统都存在静力平衡的位置,采取静平衡的方法计算系泊线的受力,(见图 1)。
|
图 1 多成分系泊静力图 Fig. 1 Static force of multi-component mooring line |
由于在每两段系泊线中间位置切线一致,分别对多成分系泊线各段积分,可推导出单根多成分系泊缆的悬链线方程如下[12]:
| $ \tan {\theta _k} = \frac{{\displaystyle\sum\limits_{i = 1}^{n + 1 - k} {{w_{n + 1 - i}}{L_{n + 1 - i}}} }}{Q}\text{,} $ | (1) |
| $ T = Q + \sum\limits_{{\rm{k}} = 1}^n {{w_k}{h_k}} = \sqrt {{{\left( {\sum\limits_{{\rm{k}} = 1}^n {{w_k}{h_k}} } \right)}^2} + {Q^2}}\text{,} $ | (2) |
| $ {{\rm{S}}_k}{\rm{ = }}\left( {Q/{w_k}} \right)\left[{{{\sinh }^{ - 1}}\left( {\tan {\theta _k}} \right) - {{\sinh }^{ - 1}}\left( {\tan {\theta _{k - 1}}} \right)} \right]\text{,} $ | (3) |
| $ S = \sum\limits_{i = 1}^n {{S_k}} \text{,} $ | (4) |
| $ {{\rm{h}}_k}{\rm{ = }}\left( {Q/{w_k}} \right)\left[{\sqrt {{{\tan }^2}{\theta _k} + 1} - \sqrt {{{\tan }^2}{\theta _{k + 1}} + 1} } \right] \text{,} $ | (5) |
| $ h = \sum\limits_{i = 1}^n {{h_k}} \text{,} $ | (6) |
| $ L = \sum\limits_{i = 1}^n {{L_k}} \text{。} $ | (7) |
以一两成分系泊线为例。系泊的材料参数如表 1 所示。
|
|
表 1 系泊材料及参数 Tab.1 Material and parameter of mooring lines |
由式(1)可以得到在当前Q情况下每段系泊与水平方向的倾角θk,进而根据式(2)计算该段系泊缆的竖直长度hk,得到每段系泊缆竖直长度的总工作水深,直到某个Q可以满足$ h = \displaystyle\sum\limits_{i = 1}^n {{h_k}} \approx 1\,000 \,{\rm{m}} $ 。对于单根系泊缆的水平力Q计算,本文结合迭代法和二分法 2 种方法进行求解。求解步骤如下:
1)取Qa=10 T,Qb=1 000 T,并取两者的中间值Qc,即$ {Q_c}{\rm{ = }}\displaystyle\frac{{{Q_a} + {Q_b}}}{2}$ ;
2)分别求出在Q取Qa、Qb、Qc时的θ1,θ2,进而求出h1,h2;
3)若$ {h_{c1}} + {h_{c1}} = 1000 $ ,则$ Q = {Q_c} $ ;若$ \left( {{h_{a1}} + {h_{a2}} - 1000} \right)*\left( {{h_{c1}} + {h_{c2}} - 1000} \right) \leqslant 0 $,则$ {Q_b}{\rm{ = }}{Q_c} $;若$ \left( {{h_{b1}} + {h_{b2}} - 1000} \right)*\left( {{h_{c1}} + {h_{c2}} - 1000} \right) \leqslant 0 $,则${Q_a}{\rm{ = }}{Q_c} $;若求需要满足一定精度的Q,则需$ \left| {{Q_a} - {Q_b}} \right| \leqslant \xi $。重复步骤 (1) ~ 步骤 (3),可得Q。具体部分Qc 值如表 3 所示;
|
|
表 2 算例 1 部分 Qc 值 Tab.2 QC of example 1 |
|
|
表 3 算例 2 部分 Qc 值 Tab.3 QC values of example 2 |

|
图 4 Qc 与 h1 + h2 关系图 Fig. 4 QC and h1 + h2 diagram |
4)分别求出式 (1) ~ 式 (7) 中各值;
5)求悬链线各点:锚链与海底接触点为原点建立直接坐标系,取水深h- 1 处的点,利用式 (8) 和式 (9) 求得对应在悬链线上的坐标。
| $ y = \left( {{T_0}/w} \right)\left( {\sqrt {{{\tan }^2}{\theta _b} + 1} - \sqrt {{{\tan }^2}{\theta _a} + 1} } \right)\text{,} $ | (8) |
| $ x = \left( {{T_0}/w} \right)\left[{{{\sinh }^{ - 1}}\left( {\tan {\theta _b}} \right) - {{\sinh }^{ - 1}}\left( {\tan {\theta _a}} \right)} \right]\text{。} $ | (9) |
式中:x和y为悬垂线段的水平距离和垂直距离;
6)逐步求解至原点,其中锚链锚索相接处需分两段求解。
通过上述步骤,可以得到式 (1)~ 式 (7) 的各个求解结果。具体值如下:单根系泊缆的水平力Q=301.293 4 T,单根系泊缆的张力T=346.236 0 T,3 段系泊缆的竖直长度为 924.312 5 m、75.687 5 m,水平长度为 2 086.5273m、472.003 6 m,系缆线与水平方向上的倾角为 0.515 2、0.312 8。可见本文中计算方法所得结果与文献[12]中的计算结果(Q= 300 T,T= 343.87 T)基本吻合。
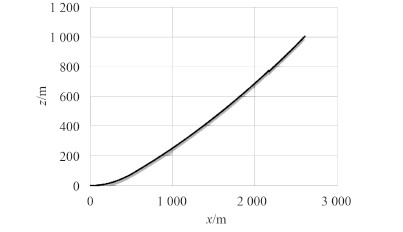
在图 2 中,随着Qc值的增加,h1 +h2逐渐变小。根据求解得到的悬链线关键数据,绘制的悬链线如图 3 所示。图 3 中的两成分悬链线中,悬垂线段的水平距离和垂直距离分别为 2 600 m 和 1 005 m,每段悬链线的斜率为系泊线在水平方向上的倾角,与系泊系统的工作参数相符合。并且下端缆索形状较为平缓,斜率较小;上端较为陡峭,斜率较大。

|
图 2 Qc 与 h1 + h2 关系图 Fig. 2 QC and h1 + h2 diagram |
|
图 3 两成分锚泊悬链线 Fig. 3 Two-components mooring lines catenary |
取一个工作水深为 2 000 m 的三成分锚泊的系泊系统,系泊缆的头尾为 500 m 的钢丝绳,其单位质量长度为 0.215 T/m;中间是一段单位长度质量为 0.0793T/m 的聚酯绳,长度为 2 000 m。参照同样方法,求解过程中的Qc值如表 3 所示。
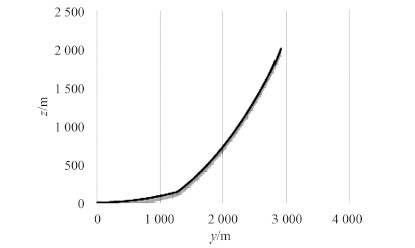
各个数值解如下:单根系泊缆的水平力Q为 176.012 6 T,单根系泊缆的张力T为 412.985 9 T,3 段系泊缆的竖直长度为 436.935 2 m、1422.454 6 m、140.6123m,水平长度为 242.195 4 m,1383.422 0 m,473.205 8 m,系缆线与水平方向上的倾角为 1.130 5,0.986 4,0.548 3。根据得到的系泊关键数据可以绘制如图 5 所示的悬链线图。
|
图 5 松弛状态下的三成分锚泊悬链线 Fig. 5 Catenary of three-component mooring lines in the relaxed state |
图 5 中的三成分悬链线中,悬链线清楚地分为3段,分别为 2 段钢丝绳和中间 1 段聚酯绳,系泊处于松弛状态。其中触底段钢丝绳形状平缓,斜率较小;中间聚酯缆的倾角大一些,但不如上端钢丝绳倾角大,自下而上总体形状呈越来越“陡峭””的趋势。
随着系泊缆的水平力Q的不断增加,系泊从松弛状态变化为张紧状态。当系泊处于张紧状态时,由三角关系可得到,系缆线与水平方向上的倾角均为 0.729 7,3 段系泊缆的竖直长度为 333.3333m,1333.3333m,333.3333m,水平长度为 372.678 0 m,1490.712 0 m,372.668 0 m。
由力的平衡关系可以得到系泊缆总湿重$ \sum {{w_i}{l_i}} $ 与系泊缆水平力Q的关系式(10):
| $ Q = \frac{{\displaystyle\sum\limits_{i = 1}^3 {{w_i}{l_i}} }}{{\tan \theta }}\text{。} $ | (10) |
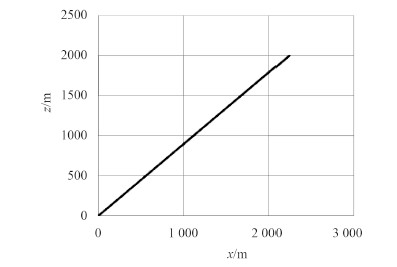
由式 (10) 得系泊缆在张紧状态下的系泊水平力Q=417.697 5 T。此时,系泊缆的形状如图 6 所示。
|
图 6 紧张状态下的三成分锚泊形状 Fig. 6 Shape of three-components mooring lines under tension |
本文给出了深水无弹性多成分悬链线方程,以工作水深 1 000 m 的两成分系泊验证方程的正确性为例,计算了工作水深 2 000 m 三成分绷紧索系泊的静力特性。根据得到的悬链线模型和关键数据,分别绘制两者的系泊缆形状图。文中的计算方法能够快速地得到具有一定精度的系泊水平力Q值,方便于深水单根多成分系泊系统的静力分析,为其进一步的动力分析提供静力基础。
| [1] |
王定亚, 朱安达. 海洋石油装备现状分析与国产化发展方向[J]. 石油机械, 2014, 42(3):33-37. WANG Ding-ya, ZHU An-da. Current situation of offshore petroleum equipment And development orientation of localization[J]. China Petroleum Machinery, 2014, 42(3):33-37. |
| [2] |
赵纪东, 郑军卫. 深水油气科技发展现状与趋势[J]. 天然气地球科学, 2013, 24(4):741-746. ZHAO Ji-dong, ZHENG Jun-wei. Development status and trends of science and technology of deepwater oil and gas[J]. Natural Gas Geoscience, 2013, 24(4):741-746. |
| [3] |
李志海, 徐兴平, 王慧丽. 海洋平台系泊系统发展[J]. 石油矿场机械, 2010, 39(5):75-78. LI Zhi-hai, XU Xing-ping, WANG Hui-li. Development of offshore platform mooring systems[J]. Oil Field Equipment, 2010, 39(5):75-78. |
| [4] | SMITH R J, MACFARLANE C J. Statics of a three component mooring line[J]. Ocean Engineering, 2001, 28(7):899-914. |
| [5] | SMITH T M, CHEN M C, RADWAN A M. Systematic data for the preliminary design of mooring systems[C]//Proceedings of the 4th international offshore mechanics and arctic engineering symposium. New York, NY:American Society of Mechanical, 1985:403-407. |
| [6] |
周洋. 深水悬链线锚泊系统多成份锚泊线设计[D]. 哈尔滨:哈尔滨工程大学, 2008. ZHOU Yang. Design for multi-component mooring line of deep water catenary mooring System[D]. Harbin:Harbin Engineering University, 2008. |
| [7] |
王冬姣. 索-链-浮子沉子组合锚泊线的静力分析[J]. 中国海洋平台, 2007, 22(6):16-20. WANG Dong-jiao. Static analysis of a wire rope-chain-buoy/sinker mooring line[J]. China Offshore Platform, 2007, 22(6):16-20. |
| [8] |
高文军, 张火明, 王强, 等. 深海平台复合单系泊缆形状和张力分析[J]. 船海工程, 2012, 41(2):161-165. GAO Wen-jun, ZHANG Huo-ming, WANG Qiang, et al. Analysis of cable single cable tension shape and composite for platforms in deep sea[J]. Ship & Ocean Engineering, 2012, 41(2):161-165. |
| [9] |
唐友刚, 易丛, 张素侠. 深海平台系缆形状和张力分析[J]. 海洋工程, 2007, 25(2):9-14. TANG You-gang, YI Cong, ZHANG Su-xia. Analysis of cable shape and cable tension for platforms in deep sea[J]. The Ocean Engineering, 2007, 25(2):9-14. |
| [10] |
张火明, 范菊, 杨建民. 复杂系泊系统静力特性快速计算方法研究[J]. 舰船科学技术, 2007, 29(3):113-118. ZHANG Huo-ming, FAN Ju, YANG Jian-min. Investigation on quick computation method of the static Characteristics of complex mooring system[J]. Ship Science and Technology, 2007, 29(3):113-118. |
| [11] |
张火明, 张晓菲, 杨建民. 基于优化思想的多成分系泊缆静力特性分析[J]. 舰船科学技术, 2010, 32(10):114-121. ZHANG Huo-ming, ZHANG Xiao-fei, YANG Jian-min. Static characteristic analysis of multi-component mooring line Based on optimization thinking[J]. Ship Science and Technology, 2010, 32(10):114-121. |
| [12] |
李志海. 深海半潜式平台多点系泊系统动力特性分析[D]. 青岛:中国石油大学(华东), 2010. LI Zhi-hai. Dynamic analysis of multi-points mooring system for semi-submersible platform[D]. Qingdao:China University of Petroleum, 2010. |
 2016, Vol. 38
2016, Vol. 38
